柔性管板计算方法与几何尺寸优化

王战辉，马向荣，高 勇，范晓勇

（1.榆林学院化学与化工学院，陕西 榆林 719000；2.陕西省低变质煤洁净利用重点实验室，陕西 榆林 719000）

1 引言

管壳式换热器是工厂中随处可见、且频繁发生破坏的压力容器。据粗略估计，每年由换热管与管板连接失效、断裂所引起过程介质泄漏与停产维修事故数不胜数，给工厂造成达上亿元损失[1]。尤其换热器中的管板，是其不可或缺的关键部件，所受载荷复杂，非常容易发生损坏，换热管区与管板的交界局部区域有时存在明显的温度梯度、应力梯度，换热设备生产运行中，在其每个部位都存在热应力，管板在设备开停车或发生紧急事故时，在很短时间内，其温度发生迅速、剧烈变化，在管板与换热管管口交界处生成强度较高的局部热应力，且应力较集中，因此，导致管板与换热管管口交界处易发生断裂，从而给设备造成极大的破坏[2]。鉴于其对于换热器的重要性，时下有大量的工厂中，对某些特殊重要的设备都开始采用柔性管板，一方面因为其采用特殊柔性材料，使它具有高韧性、高可塑性、耐腐蚀性；另一方面因为对其结构设计不断的优化改进，使它在结构尺寸、结构强度等维度又具有较大的优越性。

目前世界各国关于管板的规范标准都已形成完整的理论体系，除了这些传统压力容器设计规范不断的创新与修订，国内外出现了新的解决方法，那就是有限元法；国内外学者对管板进行了大量的研究，因换热器的工作环境条件复杂多变，管板受到的载荷多种多样，且对柔性管板这块的研究还是非常少[3-5]。

因此，笔者首先通过查找国内外管板设计标准，对柔性管板实例进行计算与对比，得出各国设计标准优点与不足；其次，利用ANSYS 软件对柔性管板进行热-应力耦合分析，得到柔性管板整体应力分布情况、各应力随结构尺寸变化规律，对柔性管板厚度T、换热管中心间距L、过渡圆角半径R 这三个因素进行了分析并进行优化，得出柔性管板的最优结构尺寸，并将优化结果应用在换热器柔性管板设计上，希望为管壳式换热器柔性管板设计领域的安全性与经济性提供依据与指导意见。

2 国内外管板设计标准与计算方法

2.1 美国TEMA 规范与日本JIS B 8243 标准

日本工业标准是以美国TEMA 规范为基础而制定的。美国的TEMA 规范和日本工业标准都是采用简单而实用的公式，且公式大同小异。

TEMA 规范是分别根据等效弹性常数定义、平板理论，总结了计算管板厚度公式。

式中：t—管板厚度，mm；F=1.25，圆板周边简支；F=1.0 圆板周边固支；G—压力作用的直径，mm；p—设计压力，MPa；μ=1-0.917（d/L）2—设计温度下的许用应力，MPa。

2.2 德国AD 标准

德国的AD 标准的前提：换热管撑持着管板，管板是被换热管撑持的平板。未排列换热管区域在很大程度上影响着管板的厚度。其计算公式为：

式中：t—管板厚度，mm；d—非布管区最大外接圆直径，mm；Pa—计算压力，MPa—设计温度下的许用应力，MPa。

2.3 GB151-1999 与JB4732-1995

首先，其规范制定借鉴了大量的外国标准，并结合本国的实际需求，在发展生产中不断的完善与创新，形成了自己独有一套地完整标准体系。其计算公式如下：

式中：K—特征系数；dJ—假想圆直径，mm；P—设计压力，MPa；ηg—许用应力修正系数，取0.85，［σ］tT—管板材料在设计温度下的许用应力，MPa。

2.4 ANSYS 有限元分析

一方面从设计方法来说，虽然国内外各个国家都已形成自己地压力容器规范体系，但是由于标准不统一以及其他因素，导致管板设计计算标准仍存在许多方面地不足：另一方面在结构优化上，由于所分析管壳式换热器柔性管板在真实生产生活中，所受载荷情况、过程流体与结构相互作用等情况极其复杂，仅仅通过理论分析与计算，所得出来地数据误差，相对来说是非常大的[6]。采用现在工程上广泛通用地ANSYS 软件、趋于成熟地有限元理论及现代计算机地辅助，使它们三者完美地结合。通过对柔性管板进行多种结构尺寸实体建模、模拟真实环境进行分析，就有较大的优越感。相比传统设计计算方法，ANSYS 设计优化精确、速度快、理论误差小。

2.5 柔性管板的相关参数

柔性管板结构与通用管板结构稍有不同，也采用了与薄管板一样设有非布管区，但设置非布管区环形区域较小，只在边缘区域（管板与过渡圆角衔接处）设置。非布管区域不会受换热管的约束，不产生较大的应力集中，将使它对过渡圆角处的挤压力大大减弱。进而让管板在设备运行过程中安全可靠性增强、使用寿命相应延长。柔性管板的物性参数、材料参数和结构尺寸，如表1～表3 所示。

表1 管板物性参数Tab.1 Physical Properties of Tube Sheet

表2 管板材料参数Tab.2 Tube Sheet Material Parameters

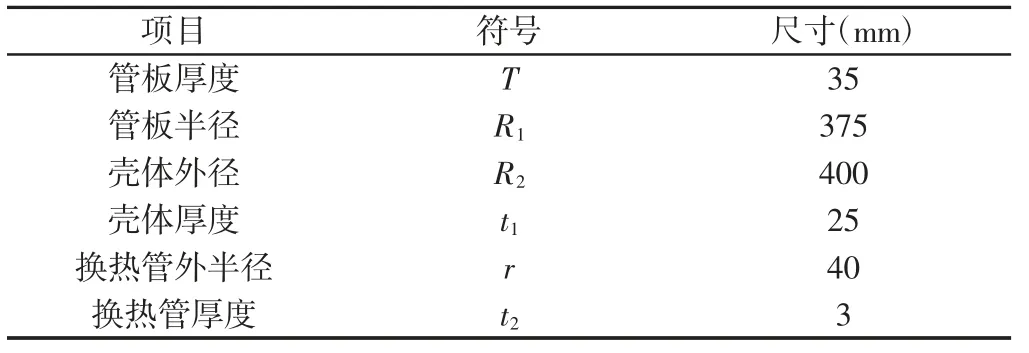
表3 管板结构尺寸Tab.3 Tube Sheet Size

2.6 国内外管板设计标准对模型的计算

以柔性管板为例，分别使用美国TEMA 标准/日本JIS B 8243标准、西德AD 规范和国内GB151 等管板厚度计算公式，计算出柔性管板的厚度。四种计算方法所得的结果如表4 所示，柔性管板厚度T 西德AD＜T 中国GB151＜T 日本JISB8243＜T 美国TEMA。

表4 柔性管板厚度计算表Tab.4 Table for Calculating Thickness of Flexible Tube Sheet

3 模拟分析与优化

3.1 柔性管板模型的选择

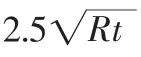
3.2 建模与网格划分

根据表3 管板结构参数，所建模型，如图1 所示。鉴于柔性管板的复杂程度，采用混合网格划分方式，自主扫掠检测，将模型主体部分划分为六面体网格、对于部分复杂程度比较高的关键部位，通过切分等多种布尔运算来划分为四面体网格，网格划分尺寸为5mm，划分网格的单元数为531500，网格划分的节点数为825580。

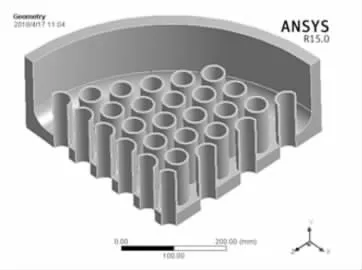
图1 柔性管板三维模型图Fig.1 Three Dimensional Model of Flexible Tube Sheet

3.3 边界条件与施加载荷

经查阅相关文献资料，换热器在生产过程中，会存在常见的七种工况。由于计算量较大，只研究其中一种正常操作工况（压力载荷与温度载荷共同作用的一种工况）来分析，从而对研究模型柔性管板进行温度场与热-应力耦合研究[7-10]。

热分析：对有限元模型设置相应条件，进行热分析（Steady-State Thermal）模块求解，得到温度场分布云图。对模型进行温度载荷的施加，在换热器管程一侧柔性管板的表面、换热管内表面施加温度为300℃，在壳程一侧柔性管板的表面、换热管外表面、壳体内表面施加温度为230℃。由于换热器除了壳体的外表面不进行换热，其它所有面都有过程介质经过，都要进行冷热流体换热，所以施加导热系数时，需注意要同时选择壳程、管程所有面。在探讨环境条件下，温度是50℃时，设置对流传热系数为19.2；温度是300℃，设置对流传热系数为22.3。

热与应力耦合分析：利用静力分析（Static Structural）模块进行求解，得到应力分布云图。将施加温度载荷所得到的温度云图的节点温度，以体载荷形式施加到静力分析模块对应的各个单元节点上，对柔性管板有限元模型施加约束，由于探讨的是1/4 柔性管板模型，存在对称截面，所以对在X、Y、Z 方向的三个截面都需要施加约束。

在柔性管板壳程一侧的壳体截面、换热管截面施加Y 方向位移为0 的约束，其他两个方向为自由；对1/4 柔性管板模型X、Z 两个截面分别施加相应地该方向位移为0 的约束，其他两个方向同样是自由。对模型施加压力载荷，对管程、壳程分别施加。在管程一侧柔性管板的表面、换热管内壁面同时施加压力载荷为4.2MPa，在壳程一侧柔性管板的表面、换热管外壁面、壳体内壁面同时施加压力载荷为0.65MPa。

3.4 温度场分布云图与应力云图

对柔性管板分别进行热分析和热与应力耦合分析，可以得到温度分布云图和应力分布云图，如图2、图3 所示。从温度分布云图可以看出，最高温度出现在换热管内壁面、管程一侧柔性管板表面，最低温度出现在壳程一侧柔性管板表面、换热管外表面。在换热管与管板交界部位、管板与壳体交界部位出现多重温度，存在较大的温度梯度，这种现象被称为表皮效应。出现此现象的原因是换热器实际生产过程中，管板该部位温度分布情况更为复杂，对施加温度载荷的模型，分析不全面，未注意到过程介质对周围固体温度分布的影响，导致此部位温度分布情况不佳。由应力云图可以看出，最大的应力出现在换热管外壁面、换热管管口与管板连接部位、过渡圆角处。壳程一侧管板表面应力强度较管程一侧管板表面大。明显看出换热管集中区域、过渡圆角段应力程度比较高，在边缘非布管区域应力程度比较低，属于过渡区域。在换热管与管板连接部位出现较模糊的应力梯度，现象不明显。综合分析，模型偏于保守，部分尺寸未达到最佳尺寸。

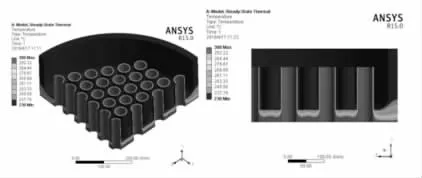
图2 温度场云图Fig.2 Temperature Field Nephogram

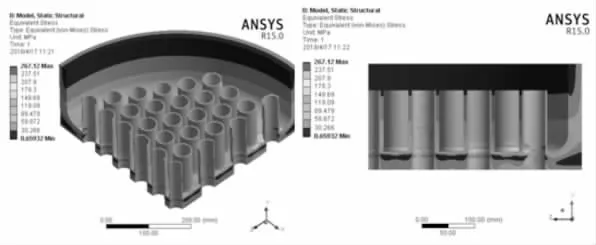
图3 应力云图Fig.3 Stress Cloud Map

3.5 结构尺寸分析及优化

为研究柔性管板关键部位的应力分布情况、得出各典型应力随结构尺寸变化图，需在危险截面选取多条路径；综合考虑在模型半径截面处，沿直径方向选取六条路径，分别为PATH1、PATH2、PATH3、PATH4、PATH5、PATH6；六条关键路径分别距离柔性管板中心距离是20mm、80mm、140mm、200mm、260mm、320mm。主要针对柔性管板的厚度、换热管中心间距、管板与壳体连接处的过渡圆角三种讨论因素共计11 种不同结构尺寸模型进行研究。

3.5.1 管板厚度

保持柔性保持管板过渡圆角R=35mm，换热管中心间距L=60mm 恒定不变，改变管板厚度，管板厚度T 分别取15mm、35mm、55mm 时，考察管板厚度对柔性管板沿直径方向各路径段的薄膜应力和薄膜加弯曲应力的影响，如图4、图5 所示。可以看出，对于薄膜应力，厚度越大，应力值越小。靠近柔性管板中心区域应力值较高，随着中心换热管过渡到边缘非布管区，应力值持续降低，在由非布管区到管板与壳体连接处也就是过渡圆角处，所对应的应力值迅速增加。三种厚度在距离管板中心距离（0～140）mm 时，走向趋势一致，缓慢降低，相对来说应力在该部分分布比较均匀。当T=15mm，在距离管板中心距离（140～260）mm 时，该条折线应力迅速降低，降幅是其他厚度变化的5 倍之多。由边缘非布管区继续沿径向到过渡圆角处，两种厚度折线在该区域的柔性管板的应力值以不同幅度增加，当T=35mm 时，在该区域应力趋势有所降低，虽然薄膜应力对于柔性管板各个应力值来说，所占的比例较小，也有模拟误差因素的存在，但仅仅从实验数据可以看出，它是符合各要求下的合适值。其中T=55mm 时，应力增加明显，而在此时达到了该条应力折线薄膜应力最大值，可达65.333MPa，分布在柔性管板过渡圆角区域。对于薄膜加弯曲应力，随厚度变化，走向趋势复杂，总体走向先趋势缓慢，接着有所降低，后趋势增加明显，柔性管板中弯曲应力占很大部分，但不能完全抛弃薄膜应力。当T=15mm，距离管板中心距离320mm 时，达到了三条薄膜加弯曲应力折线图的最大值，可达144.41MPa，同样分布在柔性管板过渡圆角区域。当T=35mm，L=60mm，R=35mm 时，薄膜加弯曲应力强度最低。比较三种厚度柔性管板关键部位的薄膜加弯曲应力折线图可得，当柔性管板厚度为35mm 时，为研究模型模拟情况最合适值。

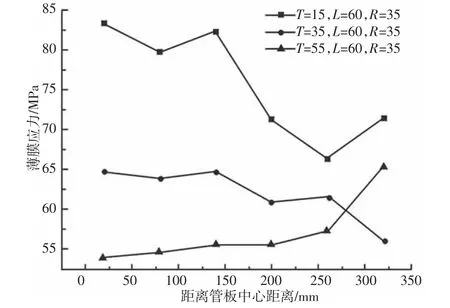
图4 薄膜应力图Fig.4 Film Stress Diagram

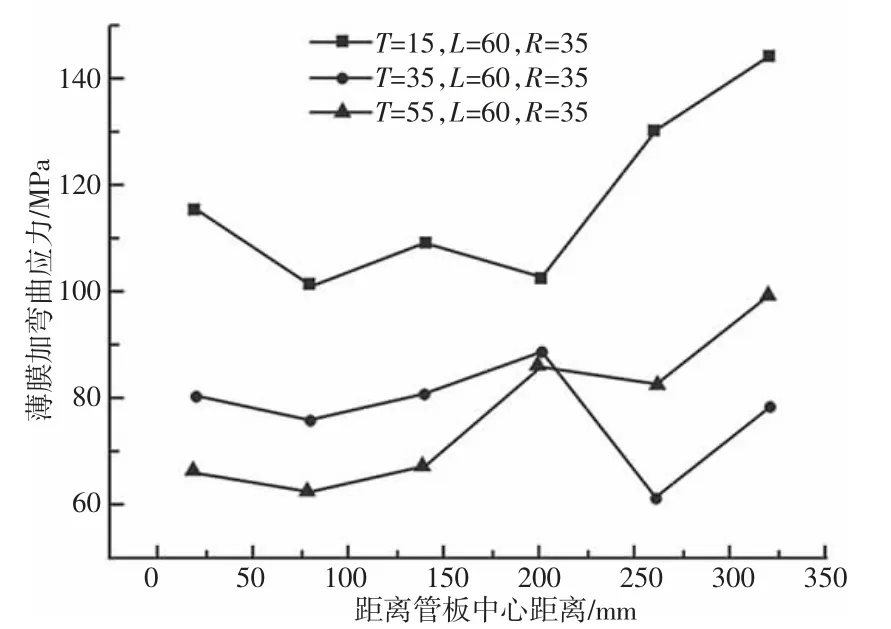
图5 薄膜加弯曲应力图Fig.5 Thin Film Plus Bending Stress Diagram

3.5.2 管板换热管中心间距

保持柔性保持管板过渡圆角R=35mm，管板厚度T=35mm 恒定不变，改变换热管中心间距L，换热管中心间距L 分别取50mm、60mm、70mm 时，考察换热管中心间距L 对柔性管板沿直径方向各路径段的薄膜应力和薄膜加弯曲应力的影响，如图6、图7 所示。可以看出，对于薄膜应力，换热管中心间距越大，应力值先保持不变后减小。三种中心间距在距离管板中心距离（0～200）mm时，走向趋势缓慢，薄膜应力值比较稳定，基本维持不变，这是由于柔性管板中心换热管布管方式是以正三角形排列，换热管布管比较均匀，不论间距如何变化，在布管区域，薄膜应力值是分布均匀的。在（200～260）mm 之间有所升高，这是由于从中间换热管区域过渡到了边缘非布管区域。在260mm 之后，L=60mm 与L=70mm 时，应力值迅速降低，降幅可达2.5 倍以上，而L=50mm 时，却随之升高。这是由于换热管中心间距增大，在换热管区域，管子对管板的约束影响增强，而对边缘非布管区域、过渡圆角处相对较低，使得该区域应力值随之迅速降低。尤其是当换热管中心间距L=60mm 时，可达23.048MPa，所对应的薄膜应力值最小，从一定程度上说明它是合适的换热管中心间距。对于薄膜应力，换热管中心间距越大，应力值先增大后减小又增大，整体随着换热管中心间距的增大，薄膜加弯曲应力值也随之增大，这由于换热管区域管子对管板的约束影响增强，从而使得每根管子周围管板的区域应力值增大。当L=70mm，距离管板中心距离（80～200）mm时，应力值增幅较大，同时达到了三条中心间距折线最大薄膜加弯曲应力值，可达112.8MPa。三条换热管中心间距变化折线，在距离管板中心距离260mm 以后，应力值都反弹增加。这由于中心换热管约束影响，束缚了管板边缘非布管区、过渡圆角处的变形，使得薄膜加弯曲应力值必然增大。当L=60mm，T=35mm，R=35mm 时，薄膜加弯曲应力值最小。比较三种换热管中心间距柔性管板关键部位的薄膜加弯曲应力折线图可得，当柔性管板换热管中心间距为60mm 时，为研究模型模拟情况最合适值。

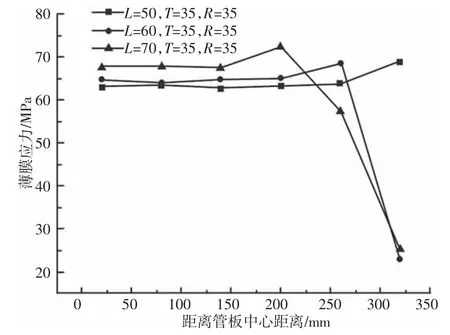
图6 薄膜应力图Fig.6 Film Stress Diagram

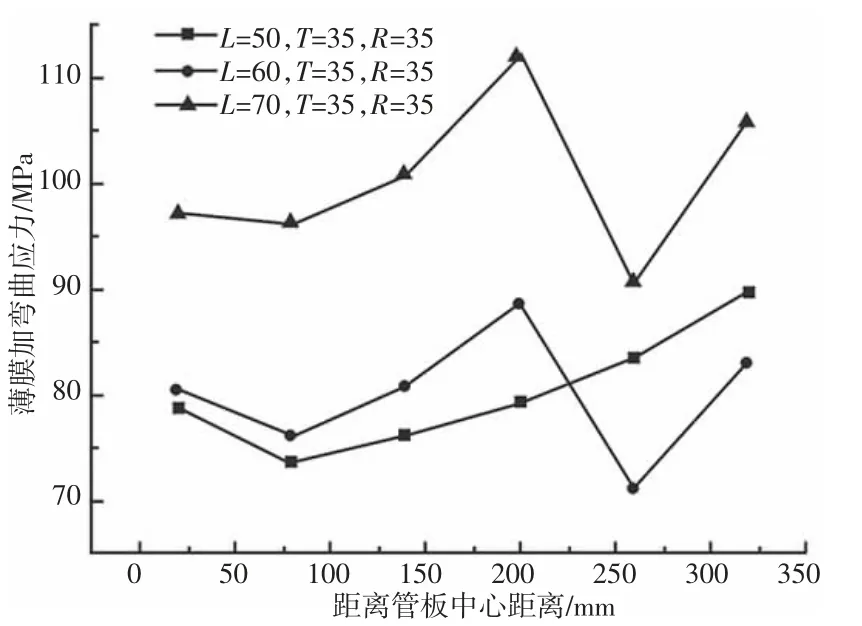
图7 薄膜加弯曲应力图Fig.7 Thin Film Plus Bending Stress Diagram

3.5.3 过渡圆角半径

保持柔性保持管板换热管中心间距合适值L=60mm，管板厚度T=35mm 恒定不变，改变过渡圆角半径R，过渡圆角半径R 分别取10mm、15mm、20mm、25mm、30mm、35mm、时，考察换过渡圆角半径R 对柔性管板沿直径方向各路径段的薄膜应力和薄膜加弯曲应力的影响，如图8 所示。可以看出，不论是薄膜应力还是薄膜加弯曲应力，随着过渡圆角半径的增大，大小基本维持不变。因此这两项应力不是影响过渡圆角处主要应力因素判断标准。

由于研究模型的局限性，得出此时过渡圆角R 为35mm，L=60mm，T=35mm 时，为研究模型模拟情况最合适值。

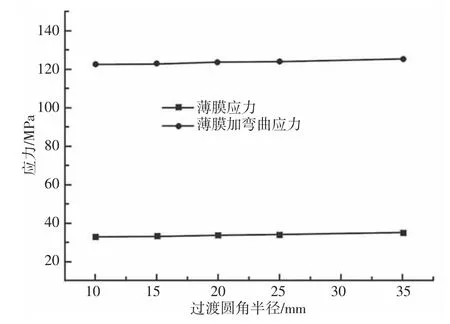
图8 各应力最大值随过渡圆角半径变化图Fig.8 Variation of Maximum Stress with Transition Fillet Radius

3.5.4 柔性管板的最优结构尺寸

柔性管板最优结构尺寸组合为T=35mm，L=60mm，R=35mm。最优结构尺寸下柔性管板的应力云图，如图9 所示。可以看出，该尺寸下最大应力减小到了217.62MPa，发生在换热管与管板的连接部位，中间换热管集中区域、过渡圆角处应力优化比较明显。

图9 最优结构尺寸的应力云图Fig.9 Stress Cloud Chart of Optimum Structural Size

3.5.5 不同计算方法的有限元验证

美国TEMA 标准、日本JIS B 8243 标准、西德AD 规范和国内GB151 四种计算方法的管板厚度计算结果如表4 所示。管板厚度T 取表4 计算结果，不改变管板物性参数和材料参数，保持柔性管板过渡圆角R=35mm，换热管中心间距L=60mm 恒定不变，取距离柔性管板中心距离200mm 的路径为研究对象，采用有限元仿真方法，考察不同计算方法对该路径的薄膜应力的影响，如图10 所示。可以看出，美国TEMA 标准管板厚度下的薄膜应力最小，西德AD 规范管板厚度下的薄膜应力最大，远离不连续区域，薄膜应力越大，管板越容易发生强度失效，安全性不容易得到保障，因此，通过有限元对比分析，西德AD 规范计算方法安全性能方面最差，不符合实际使用需求；美国TEMA 标准计算方法安全性能方面最好，更能符合实际使用需求。

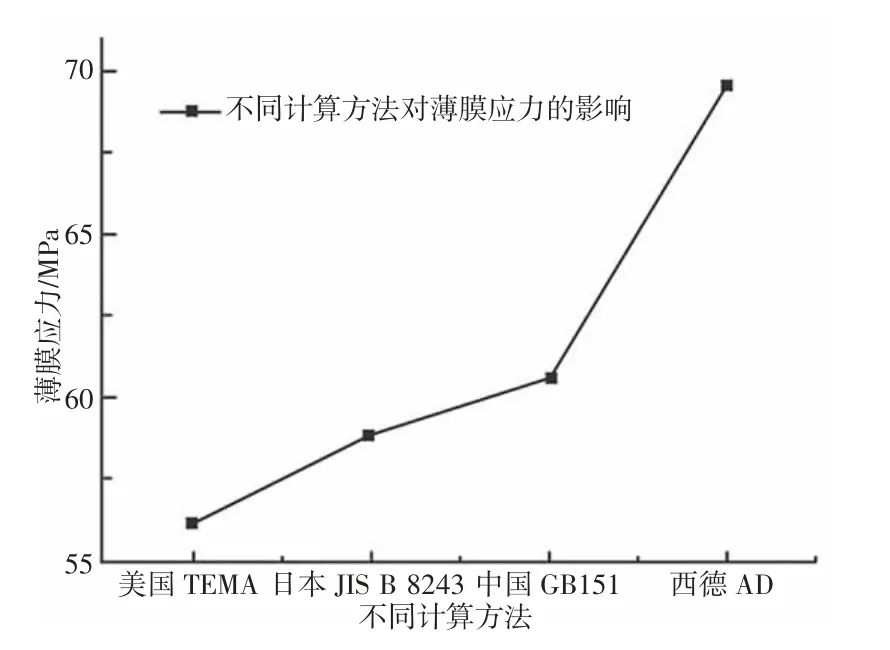
图10 不同计算方法对薄膜应力的影响Fig.10 Effect of Different Calculating Methods on the Stress of Thin Film Stress

4 结论

（1）四种计算方法所得柔性管板厚度的结果为：西德AD＜中国GB151＜日本JIS B 8243＜美国TEMA；通过有限元对比分析，西德AD 规范计算方法应力最大，容易发生强度失效，安全性最差，美国TEMA 标准计算方法应力最小，安全性能方面表现最好，更能符合实际使用需求，中国GB151 计算方法和日本JIS B 8243计算方法介于两者之间。（2）随着柔性管板厚度的增加，薄膜应力先减小后增大，薄膜加弯曲应力逐渐增大；随着换热管中心间距的增大，薄膜应力先保持不变后减小，薄膜加弯曲应力先增大后减小再增大；随着过渡圆角半径的增大，薄膜应力和薄膜加弯曲应力基本维持不变。