圆微孔及几何参数对机械密封颗粒分布的影响

陈胡炜，吉 华，李 倩，冯东林

（四川大学过程装备与安全工程系，四川 成都 610065）

1 引言

表面织构作为减少摩擦的有效手段，在理论上和实验中都被证明是有效的，普遍认为其有储油、降低静摩擦、动压效应和容渣等作用。

1996 年，文献[1]开始了微孔端面机械密封的研究，并在工业现场进行了试应用。此后，大量微织构理论与实验研究从机理和性能两个方面开展。提高承载能力的机理主要有局部空化、入口粗糙度、多孔富集效应、入口吸入、平衡楔效应等[2-3]，减少泄漏率的机理主要有反向泵送[4]、出口回吸[5]等。另一方面，采用试错法（trial and error），寻找合适的微织构形状、微孔面积比、微孔深度和微孔排布方式等，以期改善开启力、泄漏率和摩擦转矩等密封性能[2-3]。目前密封间隙多相流的研究主要基于气液两相流，针对固相颗粒在密封间隙流体中的分布的研究较少。

连续性介质模型在固液两相流动研究中应用较多，成熟稳定，计算效率较高，在固液两相润滑领域有大量的理论和应用研究[6-7]。在机械密封领域，2015 年，文献[8-10]应用连续性介质模型，对螺旋槽端面机械密封进行固液两相和气固液三相流动数值模拟，得到了密封间隙的颗粒分布规律，分析了在颗粒相存在的情况下，工况参数和几何参数对密封性能的影响。

在上述工作的基础上，基于连续性介质模型，以圆形微孔端面机械密封的间隙流体为研究对象，分析了颗粒的分布规律，并进一步讨论了不同转速下微孔面积比和微孔深度等几何参数对颗粒分布的影响。

2 计算模型

2.1 几何模型

微孔分布示意图，如图1（a）所示。其中，密封环内半径ri=24mm，外半径ro=34mm。由于微孔的周期性分布，所以选择其中任意一个周期进行数值计算，如图1（b）所示。称为计算域。每个周期均匀分布10 个微孔单元，共150 个周期。图1（c）白色部分表示B-B 截面密封间隙流体，由孔外区域和孔内区域两部分组成。微孔位于静环表面，动环转速为n，如图1 所示。

周向两面设置为周期性边界，如图1（b）所示。静环和动环表面均定义为壁面；外径处设置为压力进口，内径处设置为压力出口，外径也是颗粒相进口，颗粒浓度由颗粒进口体积分数αin指定。

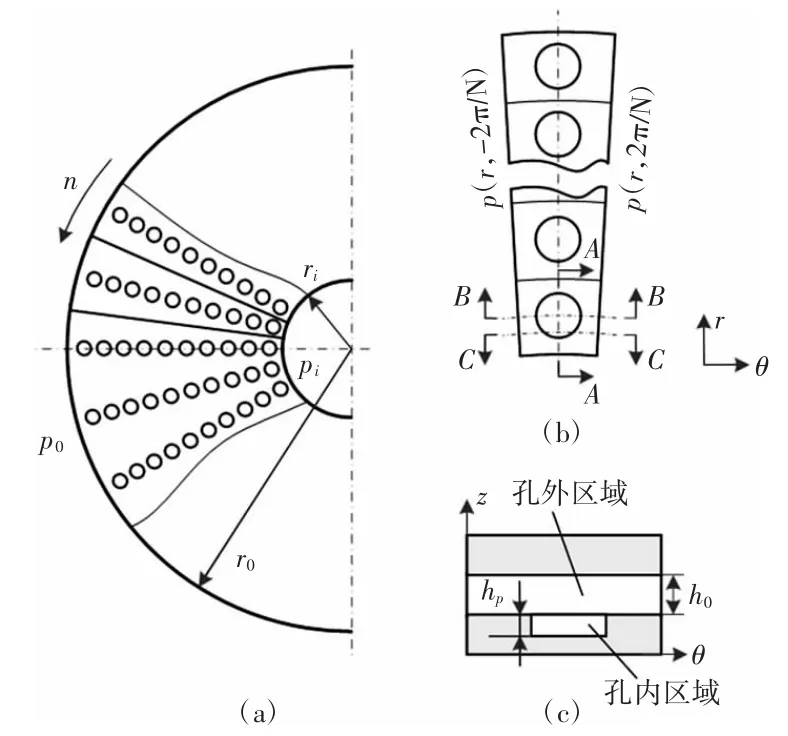
图1 微孔分布和计算域Fig.1 Micro-Dimples Distribution and Calculation Domain

采用UG 软件建立密封间隙流体的三维模型，使用ICEM CFD 进行网格划分，在Fluent 软件中进行数值计算，通过后处理软件CFD-Post 得到相关数据和云图。密封间隙流体模型r-θ 平面尺寸为毫米级，z 向尺寸为微米级，有网格跨尺度无关性问题。经过网格无关性分析，r-θ 平面网格尺寸取0.01mm，孔外区域z向网格尺寸取0.25μm，孔内区域z 向网格尺寸取0.55μm。

计算参数，如表1 所示。部分改变的计算参数的选取：第3节中，hp=5μm，Sp=20%，n=2400 r·min-1；第4.1 节中，除Sp外，其他几何参数与第3 节相同；第4.2 节中，除hp外，4.2 节的几何参数与第3 节相同。

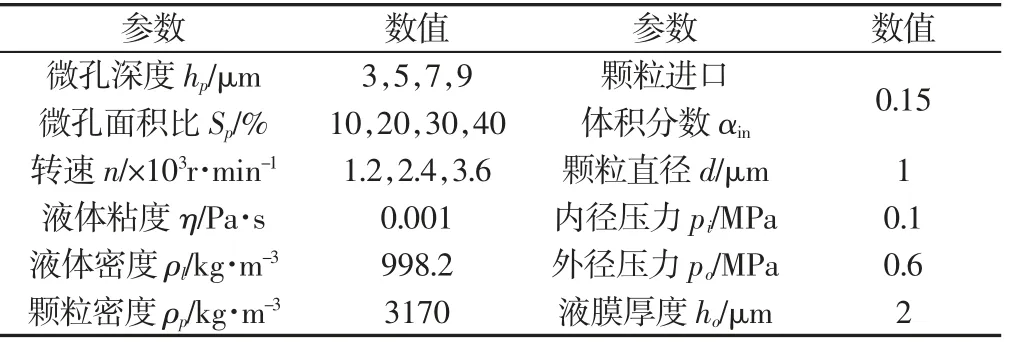
表1 计算参数Tab.1 Calculation Parameters

2.2 Fluent 求解器设置

计算假设：（1）忽略空化效应；（2）密封间隙流体流动为层流；（3）间隙流体与密封端面无相对滑动；（4）颗粒为球形，尺寸是微米级，且大小均匀；（5）忽略温度、重力的影响，密封间隙液体粘度保持不变。

采用Eulerian 多相流模型作为微孔端面密封间隙流动的计算模型，它是一种连续性介质模型，此模型用颗粒体积分数α 表示颗粒浓度。压力与速度耦合算法采用Phase Coupled SIMPLE，动量离散方法采用First order upwind，体积分数离散方法采用First order upwind。

3 密封间隙流体中颗粒分布规律

为了对比密封端面有无微孔时颗粒分布的区别，所以在这两种情况下进行了数值计算，这两种情况下靠近静环的间隙流体的压力分布和颗粒分布云图，如图2 所示。当密封环没有微孔时，从外径到内径，流体压力线性降低，颗粒体积分数α 逐渐增大，如图2（a）、图2（b）所示。存在微孔时，由于动压效应使得每个微孔单元出现了高压区和低压区，颗粒在每个微孔单元内都呈一定的规律性分布，并且这种微孔单元的颗粒分布规律从外径到内径越来越明显，如图2（c）、图2（d）所示。

图2 靠近静环的间隙流体的压力分布与颗粒分布Fig.2 Pressure Distribution and Particle Distribution of Fluid Close to Stator

在密封间隙内，由于压力在液膜厚度方向上几乎不发生变化，所以只需要选取液膜方向上的任意一个面的压力分布进行研究即可，而颗粒分布并不是如此，需研究液膜方向上的颗粒分布。由于各微孔单元内的颗粒分布规律都是相似的，所以只需选择一个微孔单元进行研究。为了研究主流动方向和密封环径向的颗粒分布规律，选择了靠近内径的微孔单元内r=24.5mm 的B-B 截面、r=24.3mm 的C-C 截面和A-A 截面进行分析，截面位置，如图1（b）所示。这3 个截面的颗粒分布及流线图，如图3、图4 所示。主流动方向为从右向左，如图3 所示。孔内区域的颗粒体积分数明显大于孔外区域的颗粒体积分数，如图3（a）所示。液体在微孔内形成了涡流，涡流中心区域位于微孔中部偏上的位置（图中白色区域Ω 所示），涡流中心区域液体基本不流动，颗粒在此区域大量聚集，形成颗粒密集区域，如图3（c）所示。

颗粒主要受到液体曳力（粘性力）和压力梯度力。在沿主流动方向切出的液膜截面上，如B-B 或C-C 截面，液体曳力占主导地位，如果只考虑液体曳力FD，其计算公式[11]为：

式中：A—与液体、颗粒的物性有关的常数；CD—曳力系数—液体速度和颗粒速度。

由式（1）可知，曳力的大小正比于液体与颗粒速度差的平方，当液体流经微孔时，液体速度发生变化，液体与颗粒间出现速度差，所以产生液体曳力，使颗粒趋向于液体的速度。当颗粒到达涡流中心区域上部位置时，液体速度变为零，颗粒因惯性进入涡流中心，并在液体曳力的作用下停下来，所以涡流中心区域聚集了大量的颗粒。由于大量颗粒进入微孔时在涡流中心区域聚集，导致进入微孔底部的颗粒较涡流中心区域要少很多，所以微孔底部液体的速度虽然也较低，但也不会有大量的颗粒停留。

图3 B-B 与C-C 截面的颗粒分布、流线图Fig.3 Particle Distribution and Streamline of Section B-B and C-C

图4 A-A 截面的颗粒分布Fig.4 Particle Distribution of Section A-A

最右侧为内径，如图4 所示。可以看出，在孔内区域，同一高度的颗粒体积分数中间小，两端大。这是由于微孔是圆形，如图3，从B-B 截面到C-C 截面，微孔沿主流动方向上的尺寸变小，所以颗粒在微孔内的流动范围和涡流中心区域的尺寸都变小，导致颗粒的聚集更加集中。又由于液体和颗粒在沿径向方向上受到压力梯度的作用，存在指向内径的分速度，所以在靠近内径的微孔端的颗粒体积分数比远离内径的微孔端的颗粒体积分数稍大，这也是整个计算域内的颗粒体积分数从外径到内径逐渐增大的原因。

4 几何参数对颗粒分布的影响

微孔端面机械密封主要通过改变微孔的形状、几何参数以及微孔的分布来提高密封性能[12]，所以研究微孔面积比和微孔深度对颗粒分布的影响。

4.1 微孔面积比对颗粒分布的影响

由于颗粒直径和密度一定，所以用颗粒总体积Vp表示颗粒量。RV是孔内区域的颗粒总体积Vpd与孔外区域的颗粒总体积Vpf的比值，即RV=Vpd/Vpf，如图5 所示。通过对比RV来研究孔内外区域的颗粒量随着几何参数的变化规律，可以看出，在不同转速下，RV都随着Sp的增大而增大。在不同转速下，颗粒分布与流线图的变化规律相似，选取n=2400r·min-1的情况进行分析，如图6所示。首先，Sp越大，颗粒密集的涡流中心区域的面积越大。这是由于Sp增大即微孔半径rp增大，沿主流动方向上微孔尺寸也增大，该方向上涡流中心区域的尺寸也增大。再者，Sp越大，微孔体积越大，导致孔内区域停留的颗粒增多。最终，RV都随着Sp的增大而增大。

图5 Sp对RV 的影响Fig.5 Effect of Sp on RV

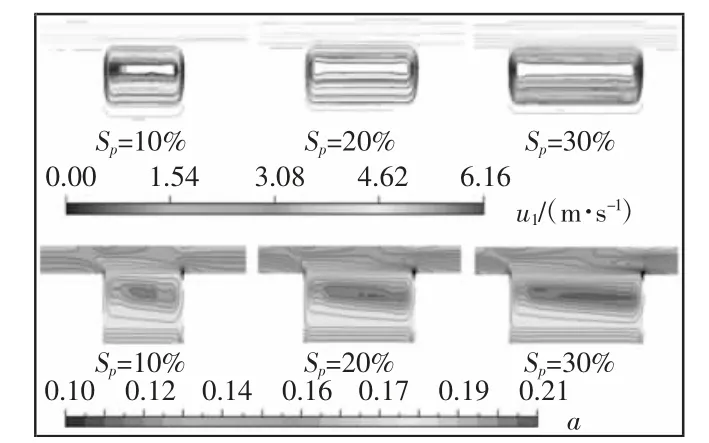
图6 Sp 对B-B 截面的颗粒分布、流线的影响（n=2400r·min-1）Fig.6 Effect of Sp on Particle Distribution and Streamline of Section B-B（n=2400r·min-1）

4.2 微孔深度对颗粒分布的影响

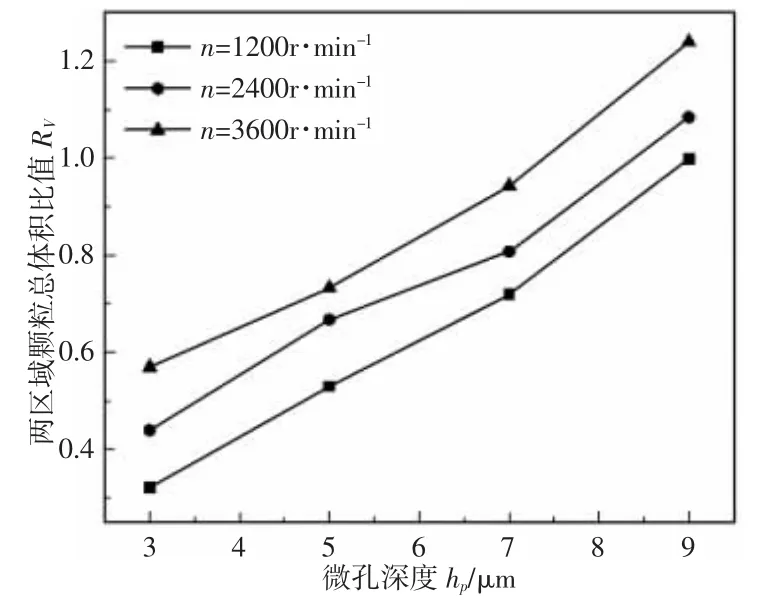
图7 hp对RV 的影响Fig.7 Effect of hp on RV

图8 hp 对B-B 截面的颗粒分布、流线图的影响（n=2400 r·min-1）Fig.8 Effect of hp on Particle Distribution and Streamline of Section B-B（n=2400r·min-1）

在不同转速下，RV都随着hp的增大而增大，这与Sp对RV的影响相似，如图7 所示。在不同转速下，颗粒分布与流线图的变化规律相似，选取n=2400r·min-1的情况进行分析，如图8 所示。hp越大，涡流中心区域面积越小，在涡流中心区域聚集的颗粒也越少，孔内区域的颗粒分布也逐渐趋于均匀。虽然涡流中心区域聚集的颗粒变少，但是因为hp增大，微孔体积增大，整个孔内区域停留的颗粒增多，所以RV随着hp的增大而增大。

5 结论

（1）机械密封端面的圆形微孔改变了密封间隙流体中颗粒的分布，颗粒在每个微孔单元内都有相似的分布规律。（2）液体在微孔内形成涡流，颗粒在涡流中心区域聚集，这是导致孔内区域颗粒体积分数大于孔外区域颗粒体积分数的主要原因。（3）几何参数对颗粒分布有影响。Sp和hp的增大都能提高孔内区域的颗粒总体积。