利用形状不变性求解改进的五参数指数型势场的能量本征值

陈文利，冯晶晶，樊亚云

(西安培华学院智能科学与信息工程学院，陕西 西安 710125)

0 引言

在低电子态情况下，Rosen-Morse势场作为非常重要的分子模型[1]可以应用到研究双原子分子的振动问题，由于Rosen-Morse模型不考虑两个原子的内壳半径，因此不可避免出现和实验数据不相符的情况.为了描述双原子分子原子半径的影响，Zhang等提出了改良型的Rosen-Morse模型[2]，设模型表达式中eαrij=λ，此模型可转为

1 束缚态本征值近似解析解

薛定谔方程可表示为

E为系统的本征值.设波函数Ψnlm(r)=unl(r)Ylm(θ,φ)/r,并代入方程(1)中，得到如下含有改进的五参数指数型势场Schrödinger方程的径向方程

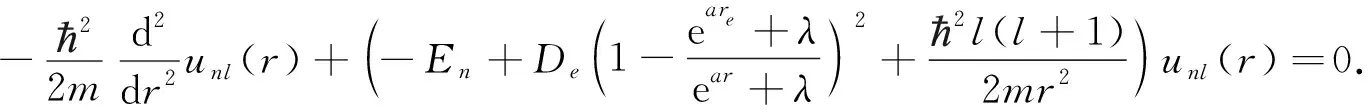
由于径向方程(3)中离心项1/r2的存在，径向方程不能解析求解，采用文献[7-8]中已推导可有效表示离心项的Pekeris型近似公式1/r2≈c0+c1/(eαr+λ)+c2/(eαr+λ)2近似表示离心项[9]，可得如下方程

其中，近似公式参数

c0=e-2αre3eαre+λ2+αreλ2-2eαreλ+e2αreαre-3/α2re4，

c1=2e-2αreeαre+λ2-λ3+αre+eαre2αre-3/α2re4，

c2=-e-2αreeαre+λ3eαreαre-3-λ3+αre/α2re4.(5)

为了应用形状不变性原理求解满足方程(4)的本征值，式(4)可化简为

其中，

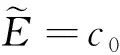
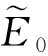
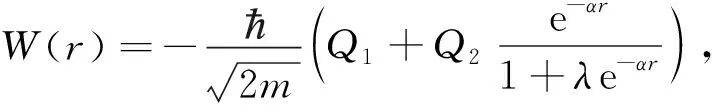
据此基态波函数可表示为

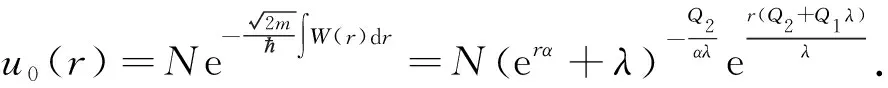
把所设超势代入方程(6)中，得如下关系:

根据方程(10)成立的条件，待定参数Q1、Q2满足:

相应的超对称伴势可表示为

对比方程(12)和方程(13),可以发现V+(r)和V-(r)满足形状不变性关系

V+(r,b0)=V-(r,b1)+R(b1)，(14)

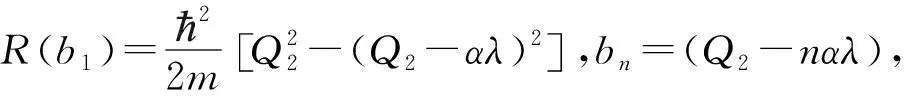
利用形状不变性理论及超对称量子力学方法，可以得到系统的能量方程为

联立方程(16)和方程(11)，可得系统本征值的解析解

2 讨论

取势参数De=2 000,α=0.15,re=1.6,λ=2,数值求解本征值方程(17)得2P态(n=0,l=1)本征值E=2.288 566，绘制了径向概率密度函数、势函数及近似公式关于r的函数图像(见图1).由图1可见，近似公式曲线和离心项曲线在势包处几乎重合，这和文献[7]中本征值数据较好地逼近了Mathematica所得数据的结论一致，同时，势包处束缚离子的几率也取到了峰值.

图1 势函数、离心项、径向概率密度、近似表达式曲线Fig.1 The plots of potential, centrifugal term, radial probability density and the approximate expression

3 结论

基于任意l态薛定谔方程求解中对中心项近似的原理，本文采用先前在求解含有改良型的Rosen-Morse模型薛定谔方程的散射态求解中已应用的Pekeris型近似公式，近似表示离心项，获得了复杂的超势.利用超对称和形状不变性的方法研究了该复杂模型的薛定谔方程本征值问题，获得本征值满足的方程，文中所得本征值方程和先前超几何函数法获得的结果是一致的.最后，绘制的近似公式、径向概率密度函数、势函数关于r的曲线图像，进一步验证本文推导的正确性.