不同水肥配比对小麦产量的影响——基于多因素响应面分析

刘 诚，季振义，江 兵，王 勇，王 刚

（1.四川农业大学商学院，四川都江堰 611830；2.四川农业大学水利水电学院，四川雅安 625014；3.四川农业大学林学院，成都 611130）

小麦是四川主要粮食作物之一，常年种植面在130万hm2左右，占所有粮食种植面积约20%，不断提高小麦产量具有重要的价值。小麦产量与水肥配比有着密不可分的重要关系。杨同荣[1]分析了氮磷钾配施对小麦产量的影响；张凤翔等[2]水肥耦合对冬小麦生长和产量的影响。杨蕊菊等[3]分析了水肥耦合对小麦产量的影响。王旭刚等[4]分析了氮磷配施对旱地小麦产量的影响。

上述文献中，不同程度存在一些尚待优化的问题，如进一步优化试验设计，考虑株高和穗粒数与千粒重的相关性；改进试验数据的处理方法，既要定量反应各因素对小麦生育形状的影响，又要深入分析因素间的交互作用，尽可能挖掘数据中的有效信息。本文拟采用多因素响应面分析法[5-11]（multifactor response surface methodology，MRSM），建立小麦株高、穗粒数和千粒重与施氮量、施磷量和灌水量的二次回归模型，并对模型进行有效性检验，分析不同水肥配比对小麦生育性状的影响，绘制响应曲面，对各因素以及因素间的交互作用进行显著性分析，同时对不同生育性状进行相关性分析，并在此基础上利用所建模型计算最优水肥配施比例，为科学增产提供依据。

1 材料和方法

1.1 数据来源

供试小麦品种为绵麦44，试验区位于四川省绵阳市安州区塔水镇。试验于2017年9月—2018年6月进行，采用响应面设计方案，试验因素与水平见表1，随机区组排列，共17个小区。试验所用氮肥为尿素（N：46%）、磷肥为磷酸二氨（P2O5：44%），所有肥料作为基肥一次性施入。灌水量1水平即不灌水；灌水量2水平为冬前灌一次水，为30 mm；灌水量3水平为冬前灌水一次，拔节期灌水一次，每次30 mm。

表1 试验因素与水平Table 1 Test factors and levels

1.2 分析方法

本研究主要采用多因素响应面分析[8]，它是通过一系列多个变量、确定性的“试验”，来模拟真实极限状态曲面的方法。设y为输出变量，xi（1，2，…，m）为输入变量，β为系数，ε为观测误差，采用二次多项式回归进行拟合（式①）。

多次观测后将①式写成矩阵形式为：

2 结果与分析

在成熟期对小麦进行取样，分别测定株高（cm）、穗粒数和千粒重（g）等生育指标，每个小区取样重复3次，求平均值，试验数据见表2。

表2 响应面试验设计与试验结果Table 2 Response interview design and test results

为了分析不同水肥配比对小麦产量的影响，利用Design-Expert 8.0.6软件，结合表2的试验数据，分别建立不同水肥配比（A为施氮量、B为施磷量、C为灌水量）对株高height、穗粒数number和千粒重weight影响的二次回归拟合曲面，并进行显著性分析。

2.1 株高响应面分析与显著性检验

对株高作二次回归，拟合曲面方程为：

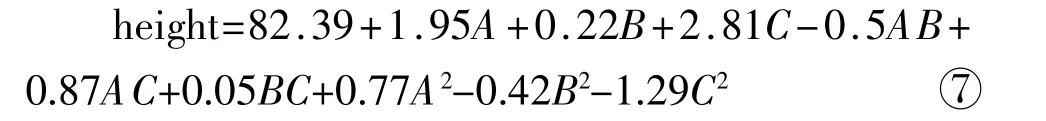
对曲面方程⑦进行显著性分析（如表3所示）和可信度分析（如表4所示）。并根据方程⑦绘制各因素交互作用对株高影响的响应曲面和等高线（如图1所示），等高线可直观反映交互作用是否显著，当等高线越呈椭圆形说明交互作用越显著，越呈圆形则交互作用越不显著。

表3 株高回归模型显著性分析Table 3 Significance analysis of plant height regression model

表4 株高回归方程可信度分析Table 4 Reliability analysis of plant height regression equation

图1 各因素交互作用对株高的响应曲面和等高线Figure 1 Response surface and contour of interaction of various factors to plant height

由表3可见，模型P=0.009＜0.01，表明拟合曲面达到极显著水平；失拟项P=0.363 5＞0.05，说明模型与实际情况拟合较好。由表4可见，相关系数R2=0.899 5，变异系数C.V.=1.6%，表明方程对试验拟合较好。

从表3和图1中可以看出，施氮量A（P=0.004）和灌水量C（P=0.000 5）对小麦株高影响极显著，施磷量B对株高影响不显著；AB、AC、BC的P值都较大，等高线几乎呈半径较大的圆形，交互作用均不显著。

2.2 穗粒数响应面分析与显著性检验

对穗粒数作二次回归，拟合方程为：

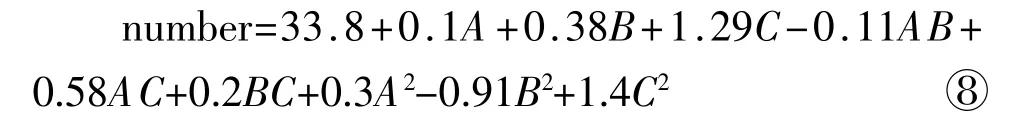
对曲面方程⑧进行显著性分析（如表5所示）和可信度分析（如表6所示）。并根据方程⑧绘制各因素交互作用对穗粒数影响的响应曲面和等高线（如图2所示）。

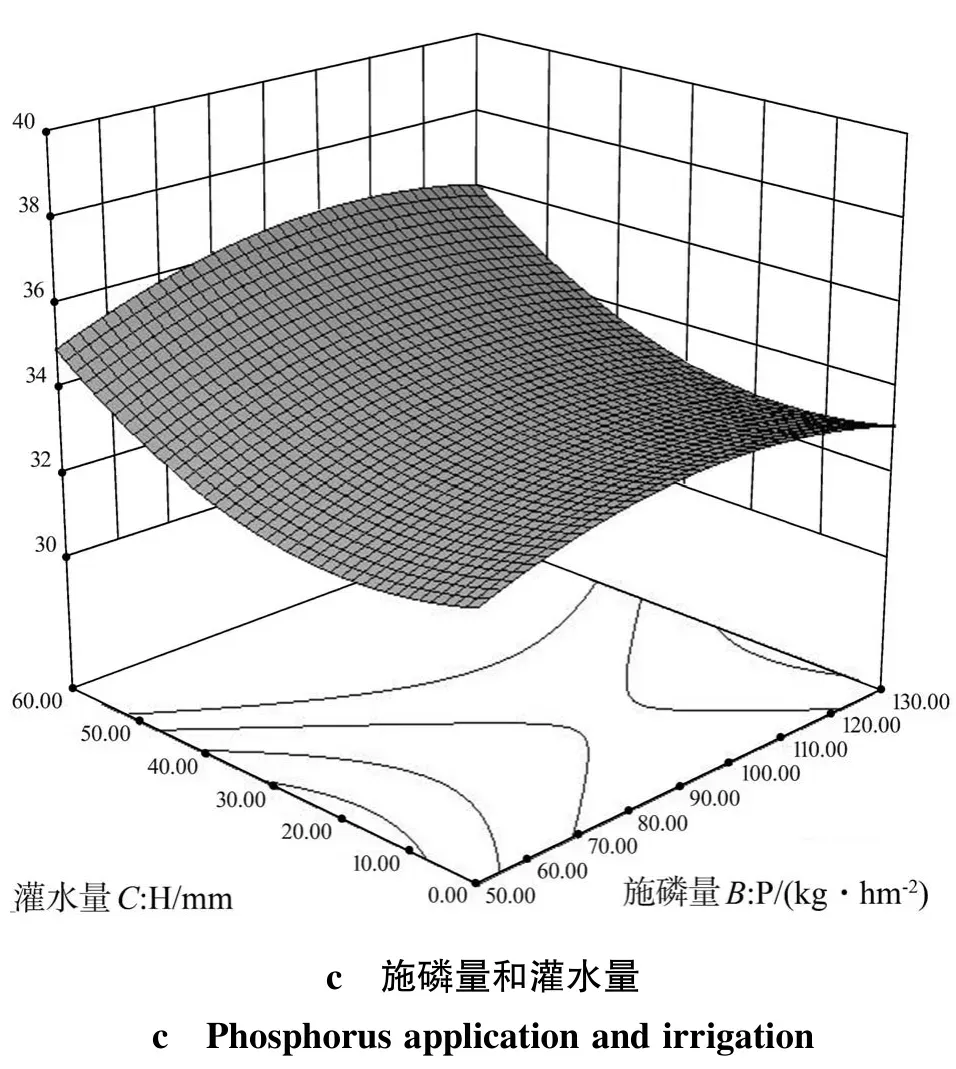
图2 各因素交互作用对穗粒数的响应曲面和等高线Figure 2 Response surface and contour of interaction of various factors to grain number per spike

表5 穗粒数回归模型显著性分析Table 5 Significance analysis of regression model for grain number per spike

表6 穗粒数回归方程可信度分析Table 6 Reliability analysis of regression equation for grain number per spike

由表 5 可见，模型 P=0.017 5∈（0.01，0.05），表明拟合曲面达到显著水平；失拟项P=0.114 3＞0.05，说明模型与实际情况拟合较好。由表6可见，相关系数R2=0.876 1，变异系数C.V.=2.22%，表明方程对试验拟合较好。

从表5和图2中可以看出，灌水量C（P=0.001 9）对小麦穗粒数的影响极显著，且灌水量C2（P=0.006 7），说明土壤湿度是决定小麦产量的决定因素；施氮量A和施磷量B对穗粒数影响不显著；施氮量和灌水量AC有一定的交互作用；AB、BC的P值都较大，等高线呈圆形，交互作用均不显著。

2.3 千粒重响应面分析与显著性检验

对千粒重作二次回归，拟合方程为：

对曲面方程⑨进行显著性分析（如表7所示）和可信度分析（如表8所示）。并根据方程⑨绘制各因素交互作用对穗粒数影响的响应曲面和等高线（如图3所示）。

表7 千粒重回归模型显著性分析Table 7 Significance analysis of 1 000-grain weight regression model

表8 千粒重回归方程可信度分析Table 8 Reliability analysis of regression equation for 1 000-grain weight

图3 各因素交互作用对千粒重的响应曲面和等高线Figure 3 Response surface and contour of interaction of various factors to 1 000-grain weight

由表7可见，模型P=0.008 4＜0.01，表明拟合曲面达到极显著水平；失拟项P=0.141＞0.05，说明模型与实际情况拟合较好。由表8可见，相关系数R2=0.901 7，变异系数C.V.=1.91%，表明方程对试验拟合较好。

从表7和图3中可以看出，施氮量A（P=0.001 4）和灌水量C（P=0.002 9）对小麦穗粒数的影响极显著，说明土壤含氮量和湿度是决定小麦产量的关键因素；施磷量B对穗粒数影响不显著；AB、AC、BC的P值都较大，等高线呈圆形，交互作用均不显著。

2.4 生育性状相关性分析及最佳水肥配施方案

为了进一步分析株高和穗粒数与千粒重之间的影响影响，建立千粒重的二元线性回归方程（式10），并对方程的显著性进行检验（表9）。结果表明，千粒重与株高和穗粒数之间存在显著的正相关关系（P=0.014），因此提高小麦的株高和穗粒数对小麦增收也极具重要性。

表9 千粒重回归方程显著性检验Table 9 Significance test of regression equation for 1 000-grain weight

结合2.1～2.3节响应面的分析，可以得到最优水肥配施方案以及相应生育性状的拟合值，如表10所示。

表10 最佳水肥配施方案Table 10 Optimum water and fertilizer combination scheme

根据上面的分析，可以确定最佳水肥配施方案为施氮量 219.68 kg/hm2，施磷量 86.61 kg/hm2，灌水量60 mm。在此方案下，各生育性状的拟合值为株高 87.519 cm，穗粒数37.527粒，千粒重47.565 g。考虑实际可操作性，调整参数为施氮量220 kg/hm2，施磷量87 kg/hm2，灌水量60 mm。在此条件下，于2018年9月—2019年6月进行试验验证，随机抽取10株测量株高和穗粒数，重复3次计算平均株高穗粒数；随机抽取5组千粒，称重并计算平均千粒重。试验结果为株高（87.48±1.63）cm，穗粒数（37.6±1.05）粒，千粒重（47.88±0.86）g。对试验结果进行误差分析（表11），结果表明试验结果与拟合值相近，千粒重误差为0.66%，说明响应面法优化水肥配比对小麦增收的应用价值。

表11 误差分析Table 11 Error analysis

3 结论与讨论

3.1 结论

本文建立了水肥配施对株高、穗粒数及千粒重的二次回归方程，绘制了响应曲面，结果表明：①本文所建立的二次回归模型效果良好，精度较高（株高：P=0.009＜0.001；穗粒数：P=0.017 5＜0.05；千粒重：P=0.008 4＜0.01）；②株高与施氮量呈极显著正相关（P=0.004＜0.01），与灌水量呈极显著正相关（P=0.000 5＜0.01）；穗粒数与施磷量呈极显著正相关（P=0.001 9＜0.01）；千粒重与施氮量呈极显著正相关（P=0.001 4＜0.01），千粒重与灌水量呈极显著正相关（P=0.002 9＜0.01）；③各因素间的交互作用不显著。

生育形状相关性分析表明：①千粒重与株高、穗粒数之间具有显著的正相关性（P=0.014＜0.05）；②最佳水肥配施方案为施氮量220 kg/hm2，施磷量87 kg/hm2，灌水量 60 mm。

3.1 讨论

作物产量一方面受到自身遗传特性和生理机能等内在因素的影响，另一方面也受到外在环境因素的影响。气候因素不易控制，水、肥控制常作为增产有效手段。研究水肥配施对小麦产量的影响，并进行合理优化，是小麦种植过程管理研究领域的热点问题。目前大部分文献均采用相关性分析、方差分析和正交试验等传统方法，尚未发现将多因素响应面分析方法用于探讨水肥配施对小麦产量的影响。本文建立氮磷水对小麦株高、穗粒数、千粒重等生育性状影响的二次响应面方程，一方面能分析单肥（水）效应以及单肥（水）增施效应，另一方面还能对水肥耦合效应进行分析，并增加了分析结果信度的检验。

本文研究也存在一些尚需进一步完善的地方：①一方面由于生育期内有效降水和灌水具有等同效应，本文选择的试验地属于干旱地区，冬春季节降水量较少，所以并未考虑降水与增产的年际效应。另一方面，不同土壤特性对作物的生长也存在很大的影响，在本研究中并未对试验区土壤特性进行分析。因此，在将来的研究中，将加入其他试验区，针对不同土壤特性，将不同生育阶段降雨量作为必要因素，对灌水量和灌水时间节点进一步分析。②本研究选择绵麦44为材料，试验材料比较单一，由于不同品种小麦具有不同的遗传特性和抗性，因此有必要在下一步研究中，就本文方法推广至多个小麦品种。③本研究只考虑了氮肥、磷肥和灌水的影响，未考虑其他化学肥料和生物肥料的影响，如配施钾肥和稻草秸秆还田的情况。