基于自适应多通道交互式多模型的高超声速滑翔飞行器跟踪方法

张君彪， 熊家军， 兰旭辉， 李凡， 陈新， 席秋实

(1.空军预警学院 预警情报系， 湖北 武汉 430000； 2.95980部队， 湖北 襄阳 441000)

0 引言

随着高超声速技术的发展，临近空间高超声速滑翔飞行器(HGV)已逐步由概念论证进入实际部署阶段，其凭借强大的纵深穿透能力、精确打击能力、侵彻贯穿能力，成为世界各军事大国竞争博弈的焦点，打破了传统的战略攻防平衡体系。对HGV的预警侦察、稳定跟踪、拦截防御将是各国面临的新挑战。因此，对HGV跟踪理论及技术进行深入研究成为了迫切需求。

对HGV进行跟踪实质上是机动目标跟踪问题，主要包括机动模型和滤波算法[1-3]。机动模型是对系统状态发展趋势的预测，根据建模机理不同，通常分为运动学模型和动力学模型[4-5]。运动学模型通常是对加速度进行不同的机动统计建模，属于经典的跟踪模型，可用于绝大部分机动目标的跟踪，主要包括匀速模型、匀加速模型、当前统计模型、Singer模型、Jerk模型等[6]。运动学模型的优点是适应性强，不需要太多先验信息，缺点是不能准确描述目标运动机理，跟踪效果对系统参数设置较为敏感。为建立更适合HGV的运动学模型，文献[7]对HGV的加速度进行周期性相关假设，提出正弦波自相关模型，保持了较高的跟踪稳定性和精度；文献[8]对HGV纵向上的机动特性进行研究，假设HGV在纵向上的加速度同时具备周期性与衰减性，提出衰减振荡自相关模型，对HGV在纵向上的机动具有较高跟踪精度。动力学模型通常从目标受力角度出发，对目标未知气动力进行建模，物理含义清晰，系统模型匹配时跟踪精度高，但需要较多先验信息，且适应性较差。文献[9]对HGV气动参数进行分析，利用转弯力参数与爬升力参数的耦合关系建立动力学模型，实现模型与机动状态的自适应匹配。文献[10]分析了气动加速度的变化规律，分别对阻力加速度、爬升力加速度、转弯力加速度进行建模，提高了跟踪精度。文献[11]建立HGV的气动参数“基准模型”和“偏差模型”，提高了加速度的估计精度。但单个模型难以较好实时匹配复杂机动或强机动目标，交互式多模型(IMM)算法由于具有多个模型，基本可以覆盖目标所有机动模式，能较好地解决这一问题，已广泛应用于目标跟踪领域[12-16]。在IMM算法中，转移概率矩阵通过直接影响内部模型之间的切换速度和交互效率，从而对跟踪的稳定性和精度产生重要影响。传统IMM算法中转移概率矩阵通常依据先验信息设定，内部元素是固定常数，无法根据后验信息实时调整，容易造成跟踪精度下降。针对这一问题，很多学者提出利用后验信息对转移概率矩阵进行实时修正以增强算法性能的方法。文献[17]提出一种利用模型概率的变化趋势修正转移概率矩阵的方法，并利用似然函数值判断模型是否发生跳转，提高了模型的切换速度和匹配模型的概率。文献[18]定义了一种模型误差压缩率，并将其推广至3个及以上模型的多模型系统中，实现转移概率矩阵的自适应调整。

为提高HGV跟踪稳定性和精度，现有公开文献中大多单纯采用多个运动学模型的交互或者多个动力学模型的交互作为跟踪模型，鲜有将运动学模型和动力学模型作为模型集进行交互的跟踪算法，没有充分发挥运动学模型与动力学模型各自的优势和特点。本文结合运动学建模适应性强和动力学建模匹配程度高的特点，分别建立HGV运动学模型和动力学模型作为模型集，并推导模型概率变化的过程，提出一种利用模型似然函数值实时修正转移概率矩阵的方法，提高匹配模型的切换效率，并利用残差边缘分布描述滤波模型在x轴、y轴和z轴3个不同维度与目标运动的匹配程度，改善传统IMM算法忽略不同维度估计残差差异的问题，提高跟踪精度。最后通过仿真实验验证本文算法的有效性。

1 跟踪模型构建

1.1 目标机动特性分析

假设大地模型为均匀圆球体，忽略地球自转影响，在半速度坐标系(VTC)中描述HGV滑翔段的运动方程[19-20]为

(1)

式中：r、λ、φ、v、θ、σ分别表示HGV的地心距、经度、纬度、速度、速度倾角及方位角；υ表示倾侧角；g为重力加速度；aD、aL分别为阻力加速度、升力加速度，

(2)

ρ为大气密度，α表示攻角，CL(α)、CD(α)分别为升力系数和阻力系数，S为目标等效截面积，m为目标质量。

HGV在临近空间进行滑翔时，主要受气动阻力、气动升力和重力的影响，气动阻力与速度方向始终相反，仅改变速度的大小，而气动升力与速度方向垂直，仅改变速度的方向，重力方向始终指向地心，既能改变速度大小又能改变速度方向。当HGV纵向平面受力达到平衡时，飞行器进行平衡滑翔，当其纵向受力不满足平衡条件时，便处于跳跃滑翔状态。当HGV进行跳跃滑翔时，目标状态量具有类周期的变化特性[21-22]。目标在上升阶段，由于重力和阻力，向上的速度逐渐减小直至为0 m/s. 此时目标处于最高点并开始下降，下降过程中空气密度逐渐增大，所受阻力逐渐增大，当阻力增大到大于重力时目标开始向下减速，直至速度为0 m/s，此时目标处于最低点并开始上升，由此完成一个周期的运动。

1.2 运动学跟踪模型构建

由于HGV跳跃滑翔时状态量的变化具有类周期特性，将加速度建模为正弦波自相关时间函数：

(3)

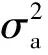
(4)

对应的状态方程如下：

(5)

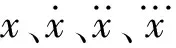
(6)

(7)

则(5)式可以写成以下形式：

(8)

设采样间隔为T，对(8)式进行离散化：

Xx(k+1)=F(T,ω0)Xx(k)+W(k)，

(9)

式中：k为时刻；F(T,ω0)为状态转移矩阵；W(k)为k时刻的过程噪声。

1.3 动力学跟踪模型构建

HGV滑翔段的加速度矢量表达式为

a=g+aa-ωe×(ωe×r)-ωe×v，

(10)

式中：a为目标加速度矢量；g为重力加速度矢量；aa为气动加速度矢量；ωe为地球自转角速度(实际计算中可忽略)矢量；r为地心距矢量；v为目标速度矢量。由(10)式可以看出，气动加速度aa是影响飞行器运动的重要因素。

在VTC中，HGV气动加速度可以表示为

(11)

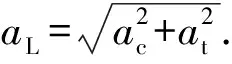
根据坐标系转换关系，在东北天坐标系(ENU)中，aa可以表示为

(12)

(13)

1.3.1 气动加速度建模

根据1.1节分析可知，HGV在无动力滑翔过程中，气动加速度随目标的跳跃呈现类周期性变化。根据以上分析对阻力加速度、升力加速度及倾侧角进行建模。将阻力加速度aD和升力加速度aL建模为正弦波形式。而倾侧角一般较小，且容易发生符号翻转，这里对倾侧角正弦值Sυ=sinυ进行建模，假设其为指数衰减形式。

1.3.1.1 阻力加速度和升力加速度建模

将阻力加速度建模为正弦波形式，则其自相关时间函数为

(14)

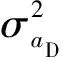
(15)

其连续时间状态方程为

(16)

由于升力加速度具有与阻力加速度相类似的变化特性，同样将其建模为正弦波形式，建模方法同阻力加速度。

1.3.1.2 倾侧角建模

为避免倾侧角翻转带来的正负值影响，这里对倾侧角正弦值进行1阶Markov建模，其自相关函数为

(17)

(18)

式中：wυ(t)为倾侧角正弦值对应的零均值高斯白噪声。

1.3.2 动力学模型状态方程

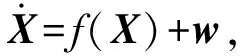
(19)

式中：w为高斯过程噪声。

非线性方程f(X)可以表示为ENU下的fENU(X)和VTC下的fVTC(X)：

(20)

(21)

式中：η为地球引力常数；B0为雷达所处地理纬度；Re为地球等效半径；ax,ENU、ay,ENU、az,ENU为气动加速度在ENU中的分量。

设采样间隔为T，对(19)式进行离散化，可得

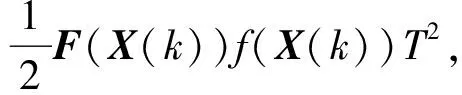
(22)

式中：F(X(k))为f(X(k))关于X(k)的雅克比矩阵。

2 自适应多通道IMM算法

2.1 IMM算法

IMM算法通常包含多个模型，能较好地适应目标的不同机动模式，并对目标状态进行有效跟踪，避免单模型匹配程度低、跟踪误差不稳定的缺点，尤其在复杂机动或强机动中效果明显。IMM算法以递推方式进行，具体过程如下：

步骤1输入交互。设j(k-1|k-1)和j(k-1|k-1)分别为k-1时刻模型j对应的状态估计和协方差，模型j的概率为μj(k-1)，Pij为模型i到模型j的转移概率，模型总个数为u.状态输入交互为

(23)

0j(k-1|k-1)=

j(k-1|k-1)][i(k-1|k-1)-
j(k-1|k-1)]Tμij(k-1)，

(24)

步骤2Kalman滤波。根据步骤1所求出的0j(k-1|k-1)和0j(k-1|k-1)，利用k时刻的量测z(k)作为滤波输入[23]，求出模型j在k时刻对应的状态估计矩阵j(k|k)及协方差矩阵j(k|k)。

步骤3模型概率更新。IMM算法中模型j对应的似然函数为

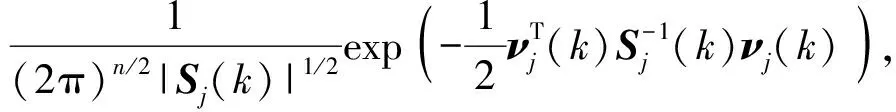
(25)

式中：n为k时刻对目标的测量次数；νj(k)和Sj(k)分别为模型j在k时刻对应的滤波残差和新息协方差矩阵。

模型后验概率为

(26)

步骤4输出交互。

(27)

(k|k)=

[j(k|k)-(k|k)]T}，

(28)

2.2 自适应转移概率矩阵

传统IMM算法假定系统模型切换符合Markov过程，即

P{Mk=Mj|Mk-1=Mi}=Pij,i,j=1,2,…,u，

(29)

式中：Mk-1和Mk分别为k-1时刻和k时刻的系统模型。传统IMM算法中，转移概率Pij是根据一定的先验信息预先给定的，且在跟踪过程中是不变的。

首先，对IMM算法中模型概率取值的变化情况进行分析，为减少复杂度，这里以两个模型集的IMM算法为例，则k时刻模型1和模型2的概率值之比可以表示为

(30)

而在任意时刻，模型概率值和转移概率矩阵都应满足以下关系式：

(31)

结合(30)式和(31)式，可以推导得到

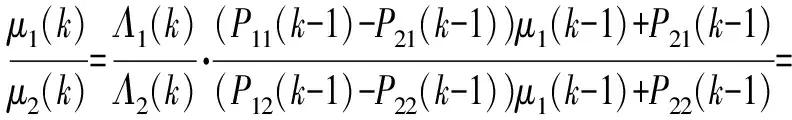
(32)

由此可以看出，IMM算法当前时刻的模型概率值与似然函数值、前一时刻的模型概率值和转移概率矩阵直接相关。其中，似然函数值是根据滤波残差和新息协方差矩阵计算出来的，反映了模型与系统的匹配程度，其比值大小直接决定了模型概率值的变化趋势，而后面的I部分可以理解为是对似然函数值之比的一个“调节器”，起到了放大或缩小似然函数比值倍数的调节作用，决定了模型的切换效率。在假设似然函数值相等的情况下对公式后面的Ⅰ部分进行研究，假设前一时刻的模型概率值不变，当前时刻模型概率值的比值随转移概率矩阵主对角线元素的变化如图1所示。

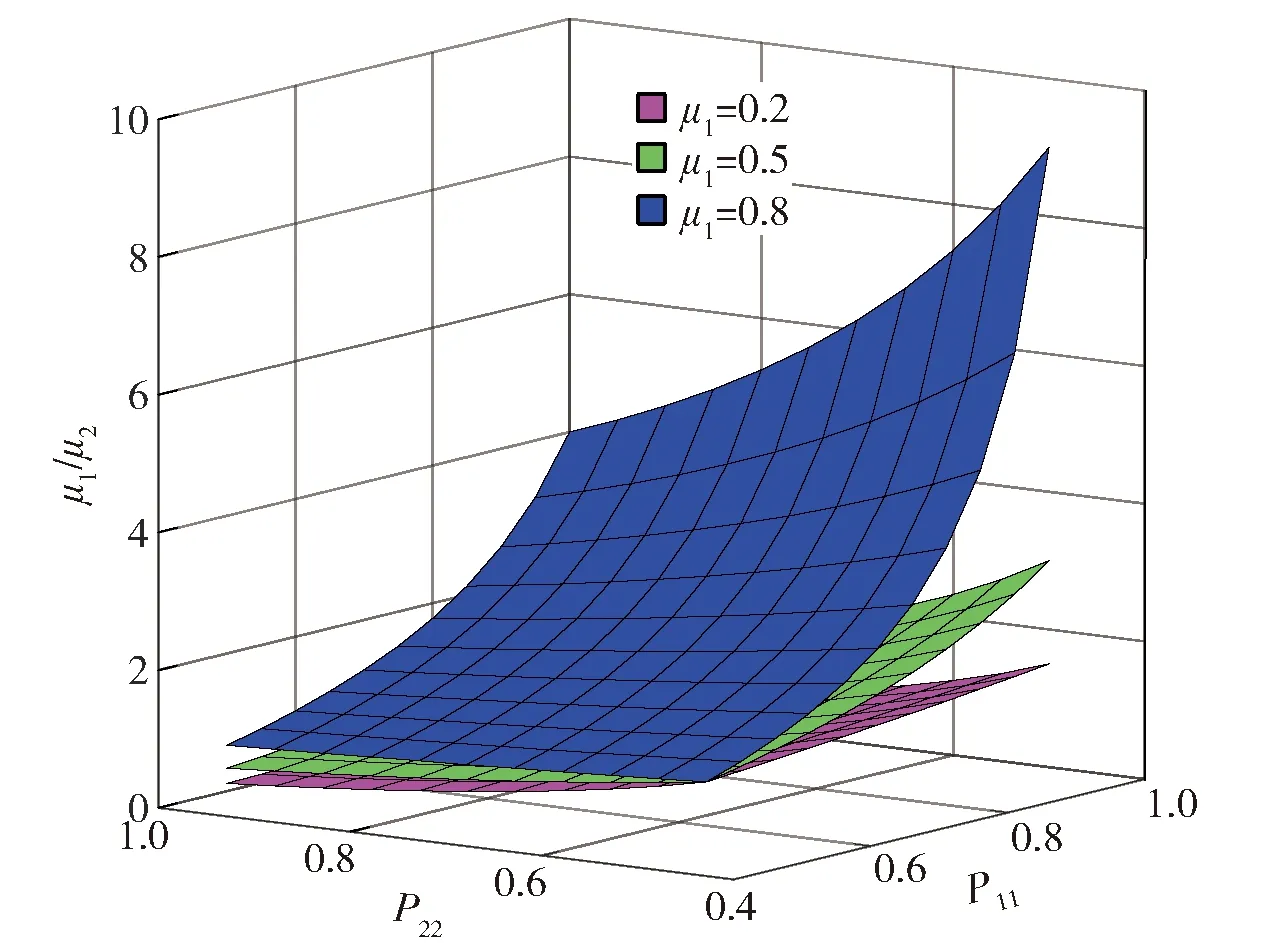
图1 模型概率比值与转移概率矩阵对角元素关系Fig.1 Relationship between model probability ratio and diagonal elements of transition probability matrix

由图1可以看出：前一时刻的模型概率值确定的情况下，模型概率的变化与转移概率矩阵紧密相关，转移概率矩阵中第i行主对角线元素越大，其他模型向该模型转移的概率越大；不论前一时刻模型概率值如何取值，转移概率矩阵对模型转移的影响在趋势上是相同的。这是因为HGV的高机动性和不确定性，使得传统IMM算法在跟踪前预先设定较为合适的转移概率矩阵尤为困难，因此，若预先设定的转移概率矩阵中的元素在HGV跟踪过程中仍然保持固定不变，则难以适应目标跟踪过程中的复杂变化，难以对模型概率值的变化进行及时准确引导，进而影响跟踪精度和稳定性。

为解决这一问题，本文提出一种利用模型似然函数值对转移概率矩阵进行调整的方法。由(25)式可以看出，似然函数值包含了滤波残差和新息协方差等信息，既能反映模型估计值与量测值之间的差异信息，又较残差更为稳定，可以直接体现模型与系统的匹配程度，决定模型概率值的变化趋势。具体计算过程如下：

(33)

(34)

P′ij(k)=φij(k)Pij(k-1)，

(35)

但是，本文修正方式可能导致转移概率矩阵中某些值越来越大，另一些值越来越小。当模型发生切换时，上述情况会导致切换速度变慢，甚至无法切换。因此，需要对转移概率矩阵中的元素值进行限定，以保持良好的性能，设定两个阈值M和N(取值范围均在0～1之间)，并做出如下修改：

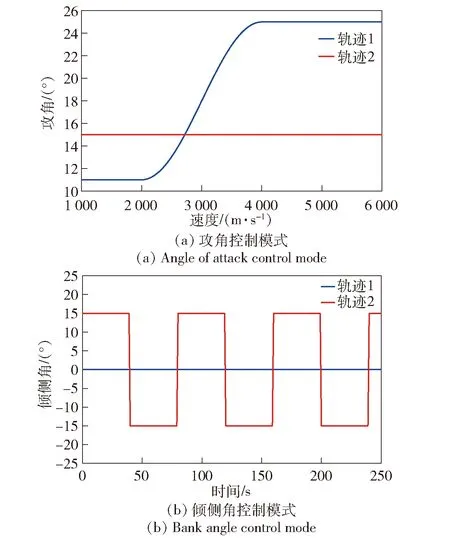
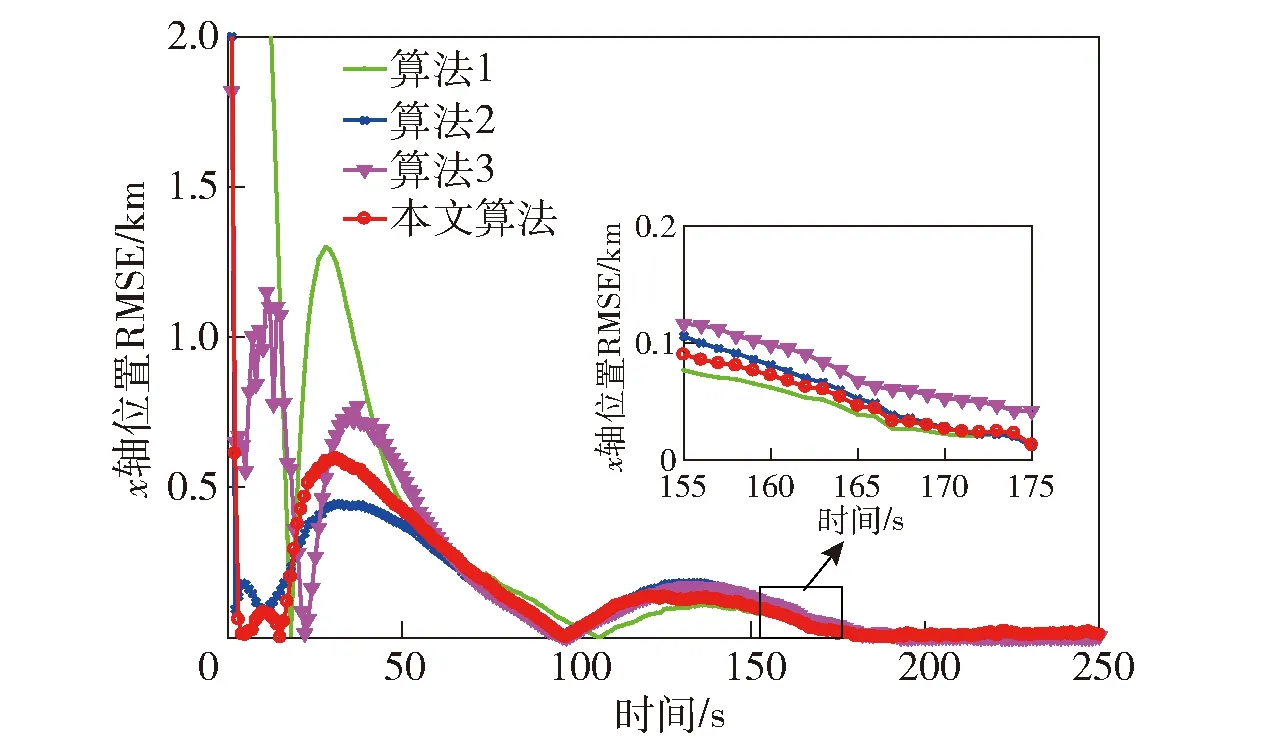
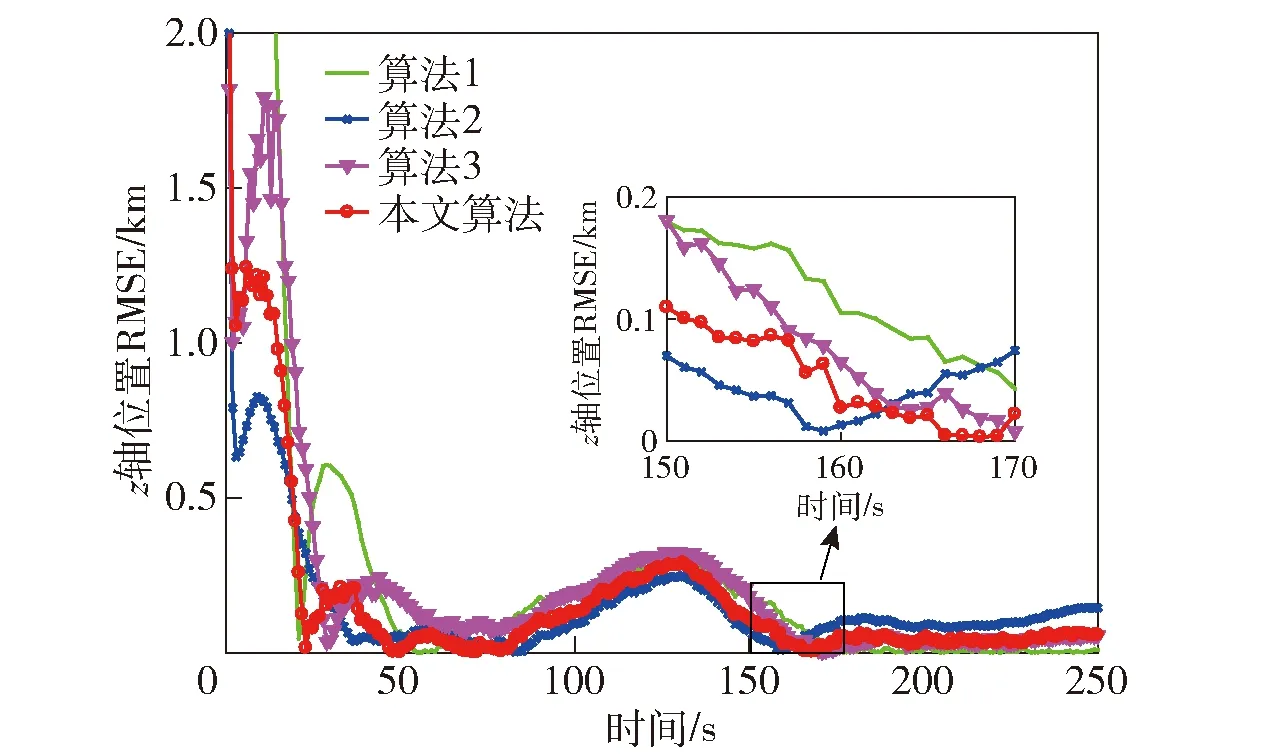
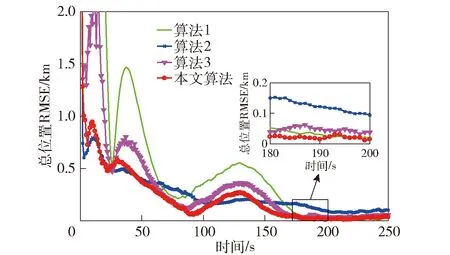
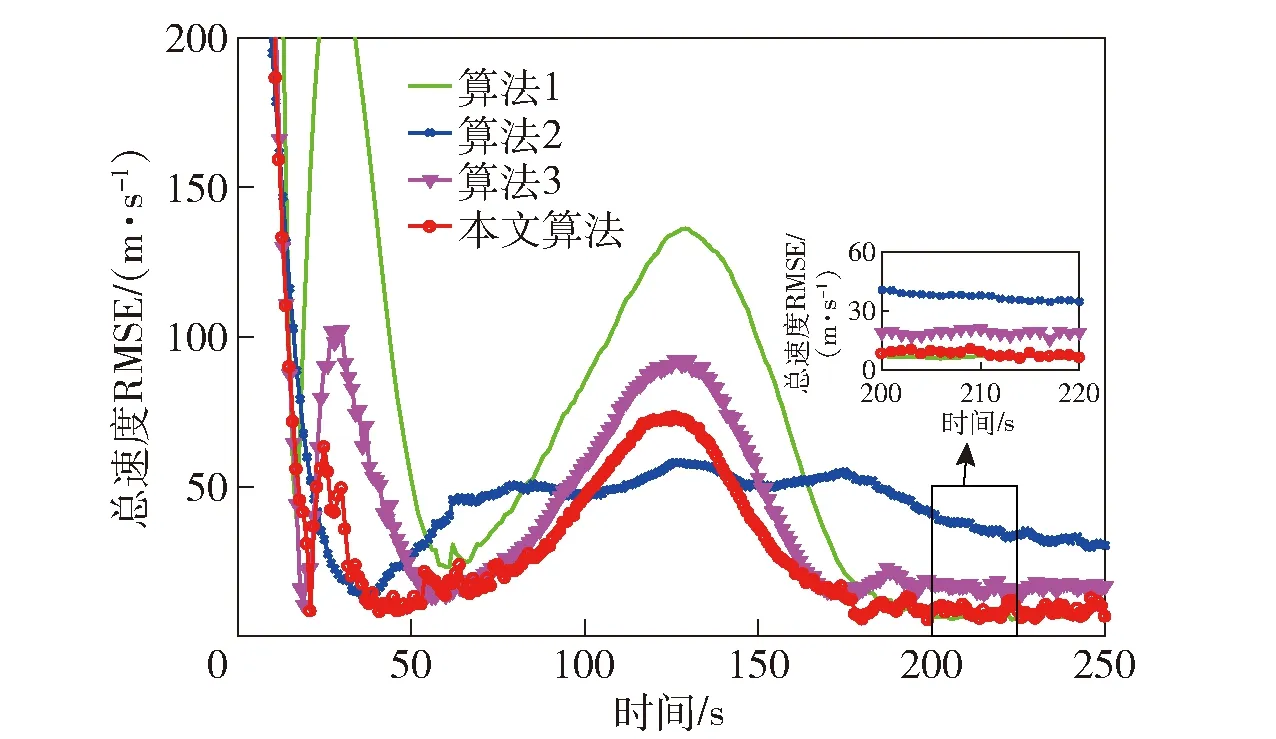
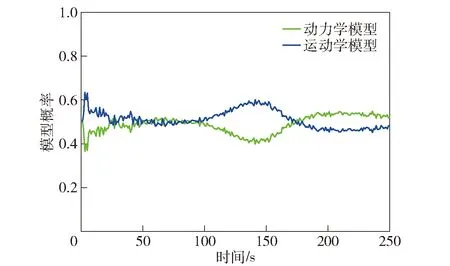
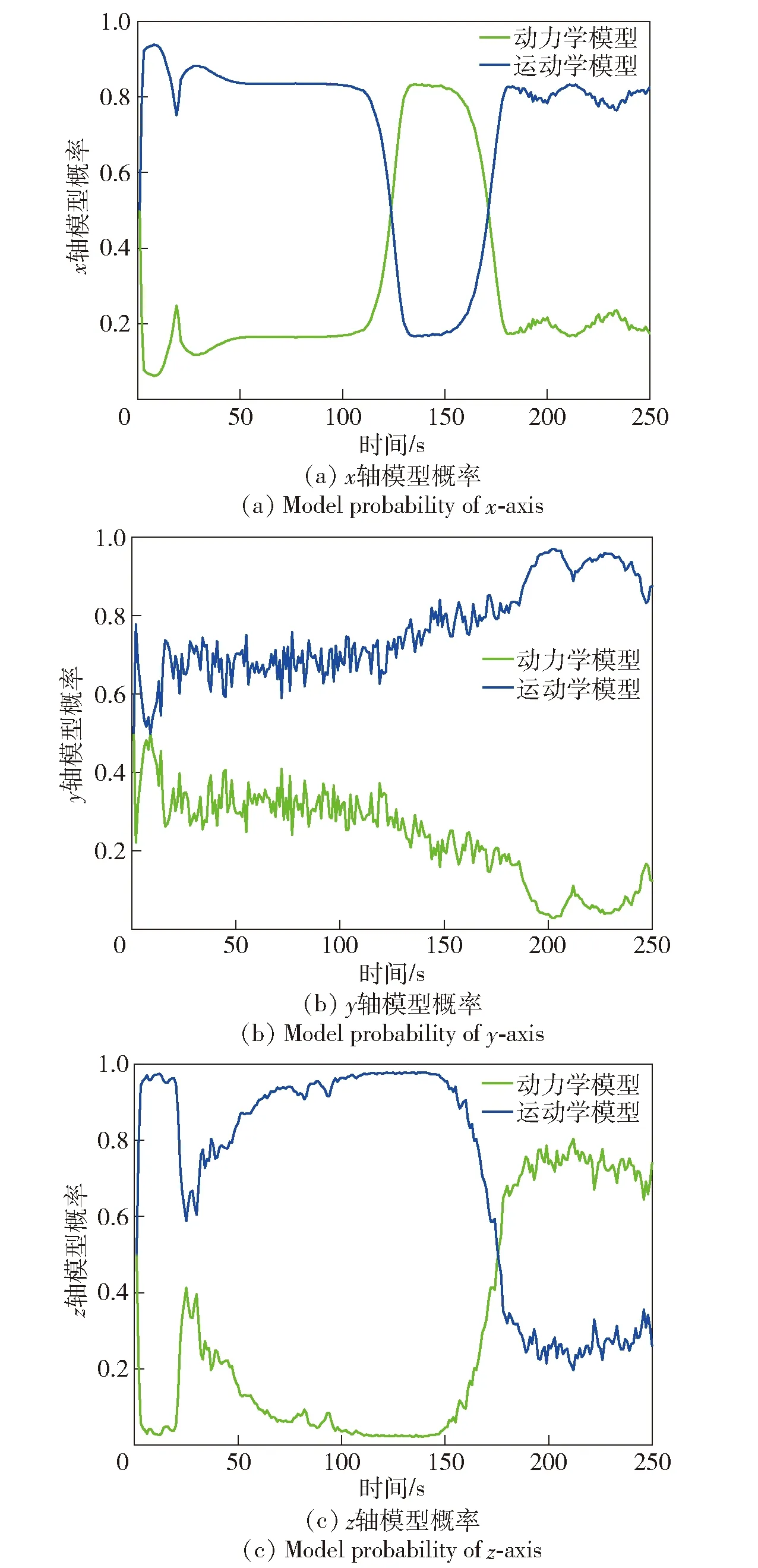
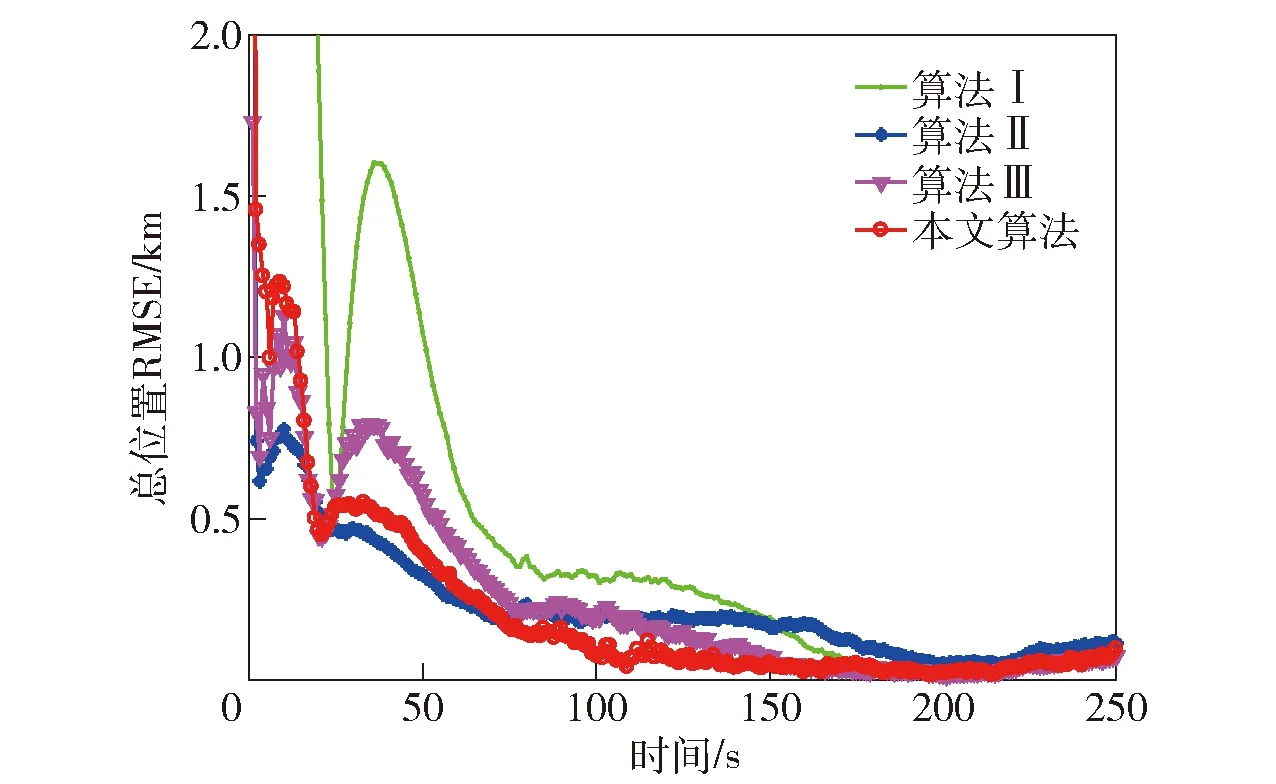
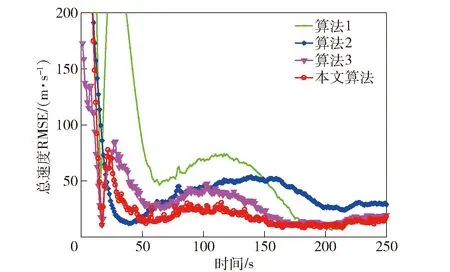
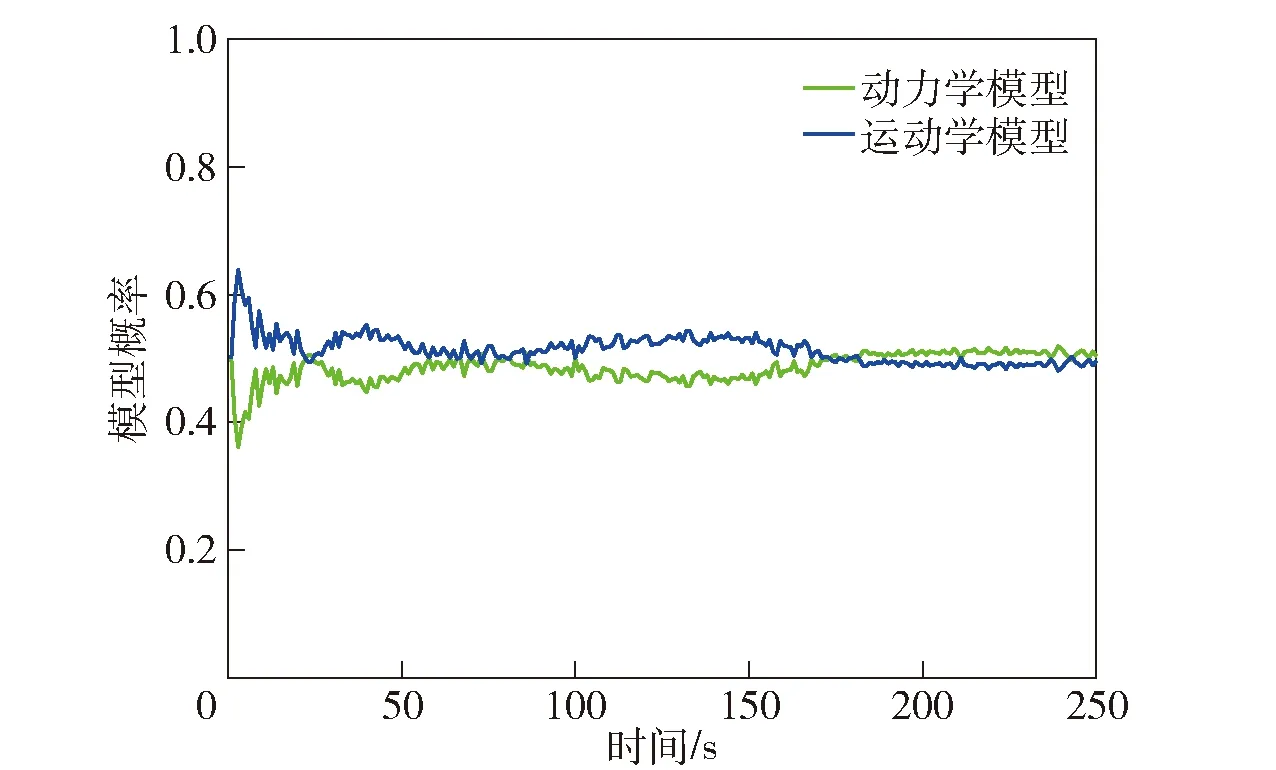
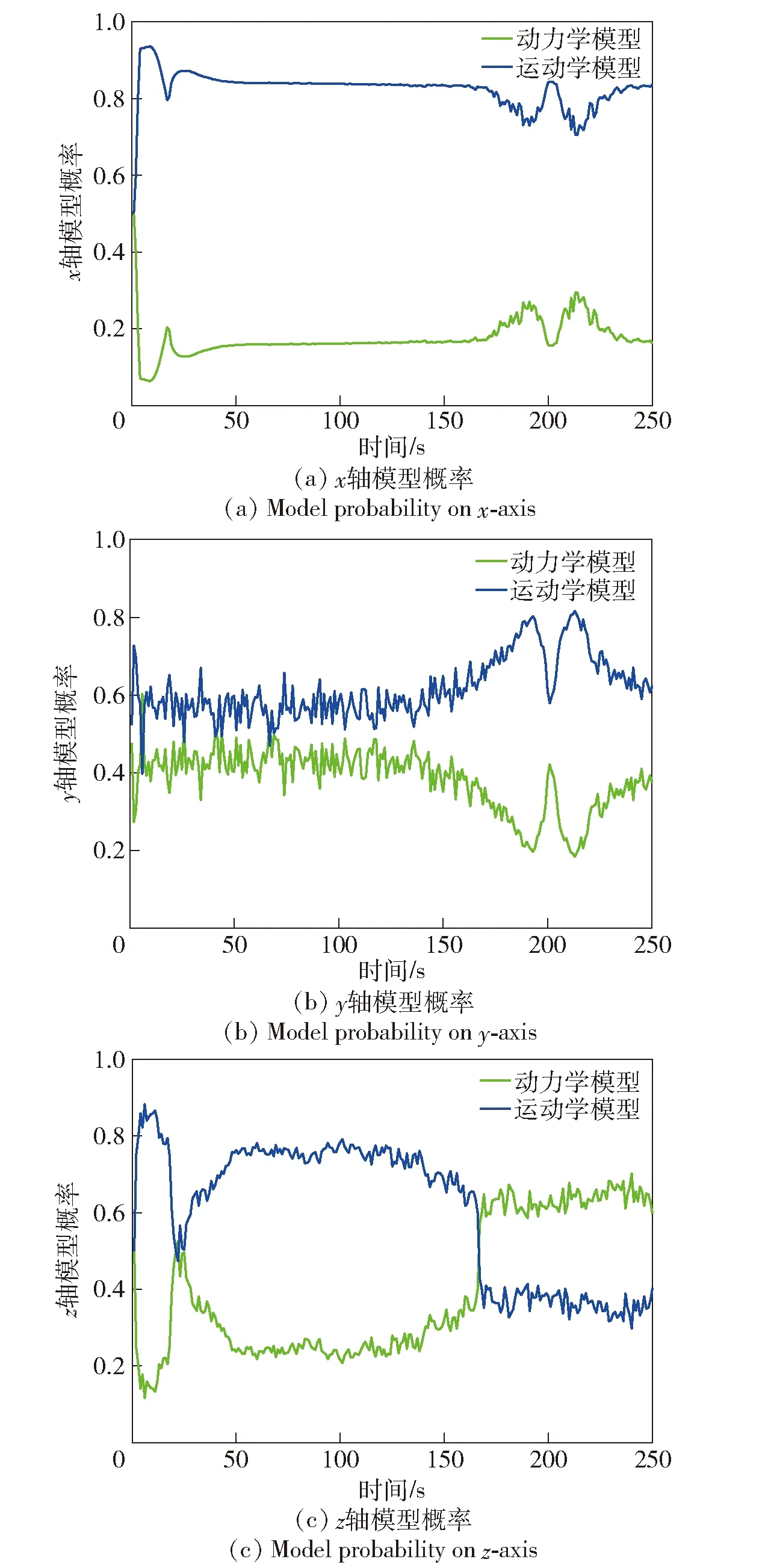
若主对角线元素Pii(k)

(36)

若非主对角线元素Pij(k)

2.3 多通道滤波

HGV跟踪属于三维跟踪，而传统IMM算法忽略了目标不同维度之间残差的差异，在求解模型更新概率时进行了无差别化处理，求得的模型似然函数值不能体现真实情况，导致跟踪误差变大[24]。若考虑模型在不同维度上的滤波差异，采用残差联合分布在不同方向上分别计算模型可能性，有利于增加模型的匹配程度，进而减小滤波误差。

这里采用残差边缘分布描述不同方向模型的可能性，则模型j在x轴维度的似然函数为

(37)

同理可以计算出模型j在y轴维度和z轴维度的似然函数，将其替代(25)式在不同方向上更新似然函数。

3 仿真实验

为验证本文算法的性能，设计两种不同攻角、倾侧角控制模式下的HGV典型机动轨迹，并与文献[10]中所提动力学模型、文献[7]中所提运动学模型、本文跟踪模型+常规IMM滤波3种算法进行对比分析。共设置两种典型控制律下的飞行器机动场景：场景1中飞行器采用零倾侧角模式，攻角建模为速度的相关函数模式；场景2中飞行器采用固定攻角模式，倾侧角为周期翻转模式。图2所示为HGV典型机动轨迹。

图2 HGV典型机动轨迹Fig.2 Typical maneuver trajectory of HGV

从图2中可以看出：场景1对应的机动轨迹1中目标纵向上进行跳跃滑翔，但其跳跃幅度和周期随攻角变化进行调整，横向上无机动；场景2对应的机动轨迹2中目标纵向上进行跳跃滑翔，横向上进行蛇形机动。这两种典型机动轨迹可用于验证本文算法在不同机动模式下的跟踪性能。图3所示为典型控制模式。

图3 典型控制模式Fig.3 Typical control mode

假设目标由发射器助推至50 km高度后释放，并按预设模式进行机动。观测雷达采样间隔为0.1 s，方位角和俯仰角误差为0.15°，距离误差为200 m，雷达所在地理坐标为[12°，0.5°，1 km]，目标始终在雷达探测范围之内且雷达探测过程中无地面遮挡。

设置4种算法分别在两种机动场景中进行跟踪，比较跟踪精度和稳定性。文献[10]中所提动力学模型为算法1(衰减系数为1/300，机动振荡频率为0.06 rad/s)；文献[7]中所提运动学模型为算法2(角速率为0.05)；本文跟踪模型+常规IMM滤波为算法3(模型参数同前面算法，初始转移概率矩阵为[0.2 0.8；0.8 0.2])；本文算法模型参数同前面算法，初始转移概率矩阵为[0.2 0.8；0.8 0.2]。交互式多模型中模型的初始化概率均为0.5. 仿真过程中其余参数的设置如下：修正速率γ为0.8，两个阈值M和N分别设定为0.7和0.05，共进行100次蒙特卡洛仿真。

3.1 实验1

利用各算法对轨迹1进行跟踪，得到位置和速度的均方根误差(RMSE)分别如图4～图8所示。由图4～图8可以看出：算法1为动力学模型，适应性较差，因此在0～150 s之间一直在进行初始化的适应性调整，误差波动较大，150 s后逐渐进入稳定跟踪阶段，误差较小；算法2为运动学模型，适应性较强，100 s后已经基本达到稳定状态，但其稳定后跟踪精度略低于算法1；算法3精度基本保持在算法1和算法2之间，初始跟踪阶段误差波动小于算法1，稳定跟踪阶段跟踪精度高于算法2，较好地发挥了动力学模型和运动学模型各自的优势；本文算法既考虑了转移概率矩阵的实时调整又考虑了不同维度上模型概率更新的差异，因此其跟踪性能优于其他3种算法，滤波收敛速度快，稳定跟踪后误差小。

图4 x轴位置RMSEFig.4 Position RMSE in x direction

图5 y轴位置RMSEFig.5 Position RMSE in y direction

图6 z轴位置RMSEFig.6 Position RMSE in z direction

图7 实验1中总位置RMSEFig.7 Total position RMSE in Experiment 1

图8 实验1中总速度RMSEFig.8 Total velocity RMSE in Experiment 1

算法3中的模型更新概率如图9所示。由图9可以看出：前期初始跟踪阶段，运动学跟踪模型由于适应性较强，滤波收敛速度快，误差波动幅度较小，属于匹配模型；后期稳定跟踪阶段，动力学模型由于精度高，属于匹配模型。

图9 实验1中算法3模型概率Fig.9 Model probability of Algorithm 3 in Experiment 1

本文算法不仅结合了运动学模型和动力学模型的优势，还考虑了目标在不同维度上运动形式及机动强度的差异，在3个坐标维度上分别进行模型的匹配优化，其各维度的模型更新概率如图10所示。从图10中可以看出，由于目标在各维度上的机动情况不同，各维度的模型更新概率也各有差别，且图4～图6所反映的算法1和算法2在不同方向上的跟踪误差与各维度上的模型更新概率基本是对应的，与目标真实机动情况更为接近，因此跟踪效果优于其他3种算法。

图10 实验1中本文算法模型概率Fig.10 Model probability of the proposed algorithm in Experiment 1

3.2 实验2

利用各算法对轨迹2进行跟踪，得到位置RMSE和速度RMSE分别如图11和图12所示。由图11和图12可以看出：算法1收敛速度慢，但后期稳定跟踪精度较高；算法2收敛速度快，但后期稳定跟踪精度较差；算法3跟踪精度和收敛速度基本介于前两者之间；本文算法具有良好的适应性，保持了稳定的跟踪性能，总体跟踪误差低于其他算法。

图11 实验2中总位置RMSEFig.11 Total position RMSE in Experiment 2

图12 实验2中总速度RMSEFig.12 Total velocity RMSE in Experiment 2

算法3中的模型更新概率如图13所示。本文算法在各维度上的模型更新概率如图14所示。由图13可以看出，由于轨迹2设定的倾侧角为周期翻转模式，在横向上进行蛇形机动，导致动力学跟踪模型在横向上难以达到较好的稳定状态。从图14中可知：x轴和y轴方向上，运动学跟踪模型始终为匹配模型；z轴方向上，动力学模型在跟踪稳定后成为匹配模型。

图13 实验2中算法3模型概率Fig.13 Model probability of Algorithm 3 in Experiment 2

图14 实验2中本文算法模型概率Fig.14 Model probability of the proposed algorithm in Experiment 2

通过实验1和实验2的仿真结果可以看出：本文由运动学模型和动力学模型所组成的模型集能够较好覆盖HGV的机动模式，所提的自适应多通道IMM算法是对传统IMM算法的扩展，增强了匹配模型所占的概率，具有自适应调节的能力；本文算法整体收敛速度较快，稳定跟踪误差较小，跟踪精度较高，整体性能优于其他3种算法。

4 结论

本文针对HGV跟踪问题提出一种自适应多通道的IMM跟踪算法。通过设计调节因子和修正速率，实现了模型似然函数值对转移概率矩阵的自适应调整；利用残差边缘分布描述滤波模型在x轴、y轴和z轴3个不同维度与目标运动的匹配程度，实现了似然函数和模型概率的一一对应。通过对典型控制律下的HGV轨迹进行跟踪实验，得出以下主要结论：

1)对于HGV这类高机动目标，充分利用运动学跟踪模型适应性强和动力学跟踪模型精度高的特点，建立IMM模型集进行跟踪是有效的，并且尽可能提高IMM模型集中匹配模型所占的概率，有利于提高跟踪精度。

2)通过似然函数值调整IMM的转移概率矩阵，在一定程度上可以提高IMM滤波算法中匹配模型所占的概率，从而提高IMM的性能。因此，相同模型集下，对转移概率矩阵进行自适应调整的IMM滤波算法跟踪性能要优于常规IMM滤波算法。

3)HGV跟踪属于三维跟踪问题，充分考虑其各维度机动情况的差异，并在各维度分别进行模型的优化匹配，更接近目标真实机动情况，能够有效降低跟踪误差，提高算法稳定性和精度。