基于演化博弈的集团化煤炭企业安全投入与监督研究

辛宪耀

(山西晋城无烟煤矿业集团有限责任公司，山西 晋城 048000)

煤炭是我国的基础能源和重要原料，煤炭资源消耗量占总能源消耗量的70%以上[1，2]，所以煤矿安全生产至关重要，而安全生产的前提是足额的安全投入。然而安全投入给企业带来的好处往往是一种间接的、潜在的、隐形的收益，而不是直接的经济收益[3]，因此高效的安全投入需要生产矿井的完全投入和集团公司的严格监督。在我国煤炭行业结构不断调整的过程中，煤矿企业集团化已经成为煤炭行业结构发展的趋势和主流[4]，在安全投入方面，我国实行统一规制下的集团公司负责制，生产矿井负责按照政府规定投入，集团公司负责监督，这种结构可能造成集团公司不严格监督和生产矿井不完全投入的问题，对我国煤炭行业结构下如何保证足额的安全投入具有较大的现实意义[5]。

目前国内外对安全投入研究已经取得了长足的进步，任海芝等人从煤炭企业安全投入规模与投入结构角度入手，提出了建立以安全投入总额最小化为目标的优化模型[6]，刘艳军等人分析了我国煤炭行业上市公司安全投入的影响因素[7]，郑毅等人从企业融资角度对煤矿安全投入的影响进行了研究[8]，李树刚等人提出了煤矿安全投入评价指标体系的构建方法[9]。另外利用博弈论研究煤矿安全投入监督近年来也引起了国内外学者的重视，国内主要有路荣武等从多总体演化博弈的角度研究了煤炭安全投入管理，研究发现政府强有力的惩罚机制是生产矿井安全投入的重要保证[10]；赵倩等人采用博弈论原理对我国煤矿安全生产监督状况进行分析，得到均衡策略组合，发现政府部门通过对违章企业加大惩罚力度，减少监督成本，加大监督概率等方法能有效提高治理效率[11]；王文轲从有限理性角度出发，建立了政府与矿井之间的演化博弈模型，发现除了惩罚机制，降低政府检查成本外，降低煤矿安全投资成本等都将使煤矿安全投入朝着良好的方向演化[12]；国外研究方面，Gray和Scholz发现将罚款数额减少会导致生产企业22%的事故增加；Leeth和Kniesner发现政府监督成本增加会减少监督机构监督检查的次数。姜福川分析了政府监督部门和煤矿管理者之间的博弈并提出了相应的投资管理对策[13]。

综上所述，国内外学者在安全投入监督监督领域集中在政府监管部门和煤矿企业之间，鲜有专家研究在政府统一规制下集团公司与生产矿井在安全投入方面的博弈关系；此外在研究方法方面，除了王文轲等人的大部分研究都以完全理性为基础进行，但在现实中，完全理性是几乎不可能达到的，集团公司依赖生产矿井创造经济效益，同时其又须监督生产矿井进行安全投入，生产矿井安全投入少可能导致集团公司为了短期的经济利益而不对生产矿井严格监督，从而导致生产矿井降低安全投入水平，造成恶性循环，从以上论述中可以看出集团公司与生产矿井并不一定能做出理性的选择，并且二者的策略选择都是在不断变化中演进的，因此使用以有限理性为基础的演化博弈进行研究更为妥当。

鉴于以上情况，本文借鉴潘峰等人建立的环境治污数学模型[14]，建立了在政府统一规制下生产矿井与集团公司的演化博弈模型，分析集团公司监督力度与生产矿井安全投入力度的影响因素，以期为确保我国煤炭行业安全投入提供一些可行性建议[15]。

1 模型假设和参数定义

1.1 模型假设

本文以在政府统一规制下的煤炭集团公司与生产矿井为研究对象，假设政府根据生产矿井的实际确定了安全投入的最低标准并且矿井按照国家最低标准执行，另外生产矿井的安全程度是由其生产规模和安全投入共同决定的，前者与安全水平呈负线性关系、后者则相反。因此，在安全技术和管理水平一定的情况下，生产矿井可以选择完全投入，也可以选择不完全投入，其策略集为{完全投入，不完全投入}，同理，集团公司可以选择严格监督下属矿井按照规定进行安全监督，也可以选择不严格监督，其策略集为{严格监督、不严格监督}。

1.2 模型参数定义

模型参数定义如下：C1为集团公司严格监督时的监督成本；C2为一线企业完全投入时的投入额；m为生产矿井生产规模决定的危险系数；n为生产矿井完全投入时危险系数的降低值；θ为政府部门根据生产规模规定的危险系数降低一个BP(指基点用于金融方面，债券和票据利率改变量的度量单位)规定的生产矿井需要的投入的最低标准额；α为集团公司考核体系中安全生产指标的权重系数，0<α<1；β为集团公司业绩考核体系中经济效益指标的权重系数，0<β<1。为了研究方便起见，假设所有参数稳定不变。

2 模型建立与分析

2.1 模型建立

设集团公司对安全投入的监督力度为λ(0≤λ≤1)，λ越小，说明集团公司监督越松，λ=0时，集团公司完全不监督；生产矿井安全投入力度为μ(0≤μ≤1)，μ越小，生产矿井的安全投入力度越低，μ=0时，生产矿井不进行安全投入。假设生产矿井选择完全投入策略的比例x，则选择不完全投入策略的比例为1-x；集团公司选择严格监督的比例为y，则选择不严格监督的比例为1-y。支付矩阵见表1，其中，p为完全投入时的危险系数，p=m-n；q为生产矿井不完全投入时的危险系数，q=m-μn。

从以上假设和分析，可以得出生产矿井的策略选择选择完全投入的期望收益：

Sk1=y(-C1-100θq)+(1-y)(-C2-100λθq)

(1)

选择不完全投入的期望收益为：

Sk2=y(-μC1-100θq)+(1-y)(-μC2-100λθq)

(2)

平均期望收益为：

根据Malthusian模型，生产矿井的复制动态方程为：

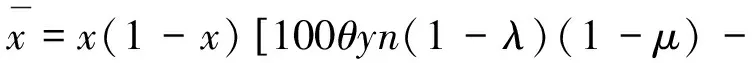
(1-μ)(C2-100λθn)]

(4)

集团公司严格监督时的期望收益为：

SJ1=x[-C1-β(C2+100θP)+100θP-αp]+

(1-x)[-C1-β(μC2+100θq)+100θq-αq]

(5)

集团公司不严格监督时的期望收益为：

Sj2=x[-λC1-β(μC2+100λθq)+100λθp-αp]+

(1-x)[-λC1-β(μC2+100λθq)+100λθq-αq]

(6)

集团公司的平均期望收益为：

集团公司的复制动态方程为：

C1(1-λ)-100xθn(1-λ)(1-μ)(1-β)]

(8)

联立式(4)和式(8)即得该模型的复制动力系统。

b=[C2-100λθn]/100θn(1-μ)

(9)

2.2 模型分析

演化均衡点的稳定性可以通过雅克比矩阵的局部稳定性分析得出，即trJ<0，detJ>0。求得雅克比矩阵如式(10)所示：

将(0，0)、(1，0)、(0，1)、(1，1)代入该矩阵可得矩阵行列式和迹(矩阵J的主对角线元素的总和)，具体取值见表2。

表2 行列式和迹的值

其中，S1=100θ(m-μn)(1-β)-C1，S1为集团公司严格监督生产矿井不完全投入时集团公司的净收益；S2=100θ(m-n)(1-β)-C2，S2为集团公司严格监督生产矿井完全投入时集团公司的净收益；S3=100θn-C3，S3为集团公司严格监督生产矿井完全投入时生产矿井的净收益；S4=100λθn-C2，S4为集团公司不严格监督生产矿井完全投入时生产矿井的净收益。以下分七种不同演化策略进行讨论：

1)当S1<0，S3<0时，其对应的演化稳定策略(不完全投入，不严格执行)如图1(a)所示，(1，0)和(0，1)是鞍点，(1，1)是不稳定点，ESS为(0，0)。

2)当S1<0，S3>0，S3<0时，其对应的演化稳定策略(不完全投入，不严格执行)如图1(b)所示，(1，0)和(1，1)是鞍点，(0，1)是不定点，ESS为(0，0)。

3)S1>0，S2<0，S3<0时，演化稳定策略(不完全投入，严格监督)如图1(c)所示，(0，0)和(1，0)是鞍点，(1，1)是不稳定点，ESS为(0，1)。

4)当S1>0，S2>0，S3<0，演化稳定策略(不完全投入，严格监督)如图1(d)所示，(0，0)和(1，1)是鞍点，(1，0)是不稳定点，ESS为(0，1)。

5)当S1>0，S2>0，S3>0，S4<0，演化稳定策略(完全投入，严格监督)如图1(e)所示，(0，0)和(0，1)是鞍点，(1，0)是不稳定点，ESS为(1，1)。

6)当S1>0，S2>0，S3>0，S4>0，演化稳定策略(完全投入，严格监督)如图1(f)所示，(1，0)和(0，1)是鞍点，(0，0)是不稳定点，ESS为(1，1)。

图1 相位图

7)当S1>0，S2<0，S3>0，S4<0，如图1(g)所示，(0，0)、(0，1)、(0，0)、(1，1)都是鞍点，没有稳定演化策略。具体情况如下：当系统的初始状态落在B区(x>a，y>b)，演化稳定点为(1，0)；当系统的初始状态落在C区(xa，yb)，演化稳定点为(1，1)，假设在博弈过程中各种情形出现的概率是完全相同的，因此则分界点坐标a越大，b越小，A区面积最大，系统向(1，1)演化的概率越大。

2.3 模型分析总结

1)通过前六种不同演化策略进行讨论，得出各种策略演化后稳定策略，第一、二种演化策略为不完全投入、不严格执行；第三、四种演化策略为不完全投入、严格监督；第五、六种演化策略为完全投入、严格监督对于前六种具有稳点演化点的情况，只有S1>0，S2>0，S3>0时，系统收敛于(1，1)，即集团公司倾向于选择严格监督，生产矿井选择完全安全投入。

2)对于特殊情况7，无稳定演化点，但是当初始状态点落在A区且A区面积越大，集团公司越倾向于严格监督、生产矿井越倾向于完全投入。

3 算例模拟验证

假设一个煤业集团和下属生产矿井，二者都是有限理性的。集团公司严格监督时的监督成本为100万元；生产矿井完全投入时的金额为4000万元；按照生产矿井的生产规模的危险系数为0.77，生产矿井完全安全投入时的危险系数降低值为0.75；生产矿井危险系数降低一个BP所需要变动安全投入为60万元；集团公司业绩考核体系中安全生产指标的权重系数和经济效益指标的权重系数分别为0.3和0.7，当下集团公司的监督力度和生产矿井的安全投入力度分别为0.75和0.80。

根据本文所建立的模型，各方在不同情况下的收益如下：

S1=6000(0.77-0.8×0.75)(1-0.7)-100=206

S2=60×100(0.77-0.75)(1-0.7)-100=-64

S3=60×0.75×100-4000=500

S4=0.75×60×100×0.75-4000=-625

据上结果，S1>0，S2<0，S3>0，S4<0，在这种情形下，没有稳定的演化策略，其分界点为(0.76，0.69)，A区面积所占比例为23.56%，即在上述所述情形下，集团公司和生产矿井有22.47%的概率倾向于完全监督和完全投入。假设将上述算例中单位BP安全投入提高为65万元，集团公司和生产矿井的监督成本和完全安全投入额降低为60万元和3800万元，经济指标在集团公司业绩考核体系中的权重降为0.65，安全生产指标提高为0.35则收益如下：

S1=6500(0.77-0.8×0.75)(1-0.65)-60=326.75

S2=65×100(0.77-0.75)(1-0.65)-60=-14.5

S3=65×0.75×100-3800=1075

S4=0.75×65×100×0.75-3800=-143.75

在上述所述情形下，分界点为(0.96，0.15)，A区面积所占比例为81.60%，集团公司和生产矿井有81.60%的概率倾向于完全监督和完全投入。从以上明显可以得出，当集团公司严格监督生产矿井不完全投入时集团公司的净收益、集团公司严格监督生产矿井完全投入时生产矿井的净收益以及集团公司不严格监督生产矿井完全投入时生产矿井的净收益上升时，临界点越靠近(1，0)，集团公司和生产矿井向良性发展的概率越大，从而证明该模型的合理性。

4 结 论

本文在博弈双方有限理性的基础上，利用演化博弈原理建立了在政府统一规制下集团公司与生产矿井的数学模型，并通过算例证明该模型的合理性。研究表明，当集团公司严格监督生产矿井不完全投入时集团公司的净收益小于零、集团公司严格监督生产矿井完全投入时集团公司的净收益大于零、集团公司严格监督生产矿井完全投入时生产矿井的净收益大于零，或为集团公司严格监督生产矿井不完全投入时集团公司的净收益大于零、集团公司严格监督生产矿井完全投入时集团公司的净收益小于零、集团公司严格监督生产矿井完全投入时生产矿井的净收益大于零、集团公司不严格监督生产矿井完全投入时生产矿井的净收益小于零。但临界点靠近(1，0)时，二者将会朝着或更大概率地朝着良性的方向发展，因此博弈双方稳定策略的选择与集团公司监督成本、生产矿井安全成本、集团公司业绩考核体系中经济指标的权重系数负相关，与单位BP安全强制投入额正相关。根据以上研究结果，得出以下结论：

1)降低集团公司的监督成本和生产矿井的安全投入成本，具体措施包括：政府对安全投入高、安全管理水平高的集团公司和生产矿井实施税收优惠政策或者对其实施经济奖励，促使双方的策略选择向良性发展。

2)调整集团公司对于生产矿井的业绩考核体系，适当降低集团公司考核体系中安全生产经济指标的权重系数、提高安全生产指标在业绩评价体系中的权重系数。如此能够激励生产矿井不会为了短期的经济利益而牺牲安全投入，并促进集团公司向严格监督演进。

3)政府部门运用法规形式提高单位安全投入和安全标准。安全标准和规定的单位安全投入越高，集团公司严格监督和生产矿井完全投入时的净收益就越高则二者越有可能向完全投入、严格监督的路径演化。