基于FP-growth算法与分层线性模型交互的招生数据挖掘

唐成龙，唐露新，杨旺功，孙道宗，薛秀云

(1. 广州理工学院招生就业处，广东广州510540； 2. 广东工业大学 机电工程学院，广东广州510006；3. 北京林业大学信息学院,北京100083； 4. 华南农业大学电子工程学院,广东广州510642)

招生工作的自动化与智能化是当前高等学校(简称高校)招生的研究热点。结合当前高校培养人才的多重因素[1]，不仅更容易通过大数据分析来获得更优的招生信息，而且通过分析历年的招生数据，结合学校人才培养模式，发挥学校专业优势及就业形势，更有利于高校吸引考生报考。招生数据挖掘应用广泛[2]，根据录取情况，结合学生考试分数、地域、所选专业及性别信息，对上述数据进行有效挖掘，对学校招生计划的制定及教学资源的配置具有指导作用。根据专业发展的需求及人才培养的历史经验数据，不同专业在录取过程中对学生进行差异化招生，是数据挖掘技术为高校人才招生提供的新的研究方向。特别是在自主招生中，根据学生个人能力、竞赛获奖及社会实践等情况，结合专业发展特点，能够更加精准地进行招生。

近年来，通过数据挖掘及大数据分析方法进行高校招生的研究成为热点，取得了一些成果。FP-growth算法作为数据挖掘常用的关联分析方法之一，在多个领域得到了广泛应用。文献[3]中针对云计算环境下的需求，提出一种改进的FP-growth算法，实现了算法的并行化，并与分布式计算框架的MapReduce模式进行有机结合。文献[4]中分析了大数据时代教育数据挖掘的新形势与传统分析模式之间的差异，指出数据挖掘技术在教育行业，特别是招生数据分析方面，具有较大的应用潜力。在国内教育领域，已有不少研究者提出使用数据挖掘算法对教育教学领域的数据进行挖掘分析。文献[5]中运用FP-growth算法对收集的贫困生数据进行数据挖掘，提高了贫困生认定工作的效率。在学校招生方面，文献[6]中提出了一种混合型贝叶斯决策树挖掘方法并应用到高职院校招生数据挖掘中，对新生报到情况进行分析与预测。目前，FP-growth算法在招生领域的应用还未见相关研究。由于高校招生数据挖掘需要结合学生层面变量与学校层面变量，分析这些变量对招生结果的影响较为困难，特别是分析这些变量与招生结果的定量关系，因此依靠单一算法很难完成。

本文中将FP-growth算法与分层线性模型相结合运用于招生数据挖掘。由于在招生数据挖掘中有2个最重要的因素，即在考生层面是招生录取期望值(录取成绩)，在学校层面是报到率，因此，首先使用FP-growth算法对报到率进行分析，根据学生数据及报到情况得到相关招生的决策支持；然后，结合学校学科及专业发展，将学校层面与考生层面相结合，充分分析学校层面变量与学生层面变量的交互影响，从而建立分层线性模型对招生期望值进行分析。

1 FP-growth算法

1.1 FP-growth算法频繁集的生成

FP-growth算法频繁集的生成主要通过扫描数据库完成[6]。以图1为例对频繁集生成过程进行说明。首先，设数据库中有12组数据集合，每组集合包含英文26个小写字母中的若干字母，将这12组原始集合称为原始集，将原始集中的每个字母进行数量统计，得到字母候选频繁集，设最小支持度为2，因此可以得到字母频繁集。

图1 FP-growth算法数据频繁集生成

FP-growth算法构造流程[7]如下：首先对数据进行统计，获得每个字母在所有元组的事务标识符(transaction identifier，TID)的统计数。然后建立二维表，从第1个TID开始，对每个字母进行计数，并将计数结果存至哈希表中，接着进行第2个TID统计，若第2个TID的字母已经在哈希表中有记录，则直接将记录中该字母的计数结果进行更新，若第2个TID的字母在当前哈希表中无记录，则将该字母添加至哈希表的末尾，并将计数结果存至哈希表中。依据此操作，遍历所有TID。

根据支持度要求，删除小于设定的支持度的字母及所对应的计数结果，并更新哈希表，同时根据计数结果从多至少的顺序对哈希表的行进行重新排列，生成新的哈希表，即FP-table，这样就可以通过序号及字母检索查询到各字母所对应的计数结果。

1.2 FP-growth算法的关联规则挖掘

FP-growth算法在对频繁模式树(FP-tree)实现第1次遍历后，对原始集合的所有项进行计数，根据计数结果与设置的最小支持度，对原始集合进行整理，就可以得到去掉了非频繁集合的数据集合。表1所示为以8棵FP-tree为例描述FP-growth算法的关联挖掘过程。

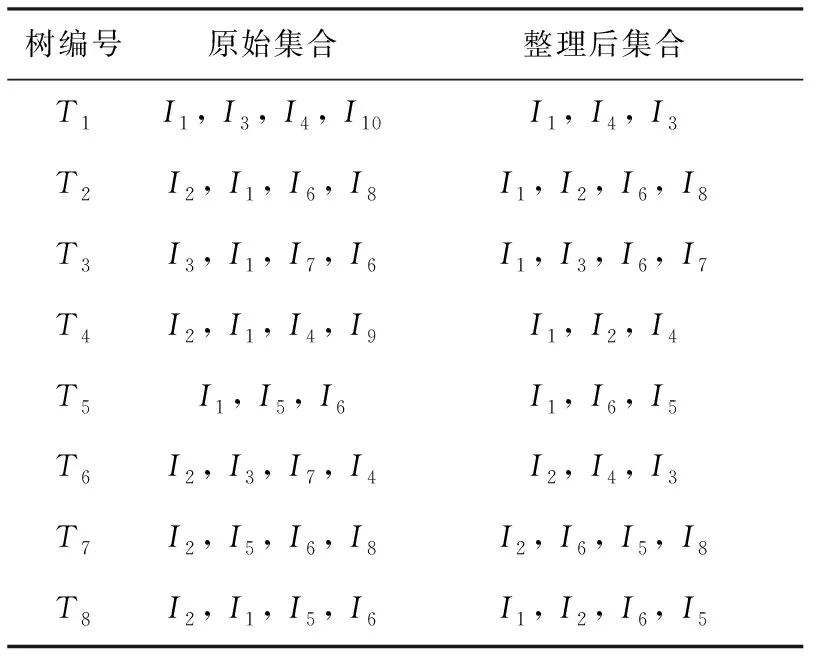
表1 FP-growth算法的关联挖掘过程

由表可以看出，在对8棵FP-tree进行第1次遍历时，对集合中较多的项进行计数统计，其中集合I9、I10的支持度均为1，集合I7、I8的支持度为2，小于设定的最小支持度3，因此经过FP-growth算法整理后的集合删除这4项，对FP-tree进行更新，并且根据支持度大小进行递减排序。第1次遍历后得到的项头表如表2所示。

表2 频繁模式树(FP-tree)算法项头表

再次扫描数据库，对频繁集进行统计，例如扫描到T2时，〈I2、I1〉、〈I2、I6〉、〈I2、I8〉、〈I1、I6〉、〈I1、I8〉、〈I6、I8〉的各项计数加1。根据遍历结果，可以得到计数矩阵[8-9]。根据计数矩阵，可以得到每个项的频繁集及多对应支持度值，根据频繁集及支持度得到关联规则挖掘结果。

2 分层线性模型

2.1 单层线性模型

分层模型的单层基础模型只考虑单因素对模型目标值的影响[10]，设Yij为第j个学校对第i个考生的录取期望值，β0j为第j个(j代表的是同一个挖掘值)学校中所有报考该校考生的平均录取期望值，rij为第j个学校的第i个考生的录取差异，服从正态分布N(0,δ2)，方差var(rij)=δ2，那么单层基础模型的计算方法[11]为

Yij=β0j+rij，

(1)

β0j=γ00+u0j，

(2)

式中：γ00为所有同类学校中所有报考该类校考生的平均录取期望值；u0j为第j个学校在学校层的差异。

var(β0j)=var(u0j)=τ00，

(3)

var(Yij)=var(rij+u0j)=δ2+τ00，

(4)

式中τ00为平均录取期望值之间的差值。

求解组内相关系数(ICC)ρ的公式[12]为

(5)

2.2 分层线性模型交互的招生数据挖掘

为了进一步挖掘高校招生数据，充分考虑学生能力及学校因素，分别从学生层和学校层建立分层线性模型。

本文中以高校理工科专业招生为例，对理工科专业的定义学生综合能力指标，如表3所示。

表3 高等学校理工科学生综合能力指标

以学生综合能力指标N1、N2、N3和N4作为第1层变量。在单层基础模型增加一层，以便更好地反映学校层面因素对招生录取带来的影响。学校层面变量如表4所示。以学校层面变量m1、m2、m3、m4和m5作为第2层变量，建立以录取率为因变量的多层线性模型(HLM)。

表4 学校层面变量

参照式(1)，HLM计算方法[13-14]为

(6)

β0j=γ00+γ01(m1)+γ02(m2)+γ03(m3)+

γ04(m4)+γ05(m5) ，

(7)

β1j=γ10+γ11(m1)+γ12(m2)+γ13(m3)+

γ14(m4)+γ15(m5) ，

(8)

3 实例仿真

为了验证FP-growth算法与分层线性模型对招生数据挖掘的性能，首先在MATLAB平台采用FP-growth算法对某高校2018年度的招生数据进行仿真，分析该校2018年度学生的报到率； 然后运用HLM对不同高校2018年度的8 671个数据进行建模分析。

3.1 基于FP-growth算法的招生仿真

选取某高校2018年度招生数据集作为仿真对象，其中数据集数据个数为3 886，训练集数据个数为586，测试集数据个数为3 300。

考虑考生成绩S、专业M、生源地D等对报到情况的影响，将考生正常报到设为T，未报到设为F。根据FP-growth算法得到频繁集，计算频繁集的支持度，由于篇幅所限，因此表5中只列出部分频繁集的支持度。

通过统计可知该校的报到率均维持在80%以上，因此将最小置信度设为80%，由此筛选出符合最小置信度的数据挖掘关联规则如表6所示。从表中数据可以看出，该校计算机专业的报到率超过了90%，表明该专业在该校的招生方面优势明显。从该校官网上可以看到，该校的计算机专业是国家重点学科，师资队伍和教学资源都是实力最强的，因此深受考生青睐。该校在华南、华中和华北地区的招生情况较好，报到率均超过了85%，而东北、东南、西南和西北地区的考生报到率略差。在报到率大于80%的14条关联规则记录中，专业主要集中在建筑、工程管理、计算机、通信工程等，这与该校是以理工科为主的背景一致。

表5 频繁集支持度

表6 关联规则表

3.2 分层线性模型的招生数据仿真

将考生成绩、所选专业、生源地等变量和学生报到率采用FP-growth算法进行置信分析，可以根据学生数据及报到情况得到相关招生的决策支持。如果从学校学科及专业发展考虑，可以将学校层面与考生层面相结合，充分考虑到学校层面变量与学生层面变量的交互影响，建立分层线性模型。

选取8 671个样本作为仿真对象，其中231个未录取样本，8 440个录取样本，然后进行样本初始化，数据集如表7所示。

表7 数据样本集分布

采用HLM7.0软件建立模型，输入8 671个数据样本，计算模型的显著性水平p值及系数[15]，p值小于0.05时模型才显著。

3.2.1 学生层面变量分析

首先对影响招生录取的4个学生层面变量进行HLM分析，统计结果如表8所示。从表中数据可以看出，学生考试成绩、获奖情况、科技创新及社会实践均正向影响考生的招生录取，即当N1、N2、N3和N4数值越大，该考生越容易被录取，而且N1的系数最大，表明在录取的学生中，学生的考试成绩仍占据最重要的地位。从p值来看，与学生考试成绩和竞赛获奖相比，科技创新和社会实践对学生的录取影响较小，这也符合我国的招生实际情况，考试分数高且奥林匹克竞赛等获奖的学生更受学校青睐。相比之下，科技创新与社会实践影响较小，与学校招生的侧重点有关，同时也与学生在这2个方面的关注度及取得的成果数量有关。从标准差来看，在录取过程中，学生的社会实践成绩差距并不大，考试成绩分布更分散。

表8 分层线性模型的学生层面变量分析

3.2.2 学校层面变量分析

对影响招生录取的5个学校变量进行HLM分析，统计结果如表9所示。

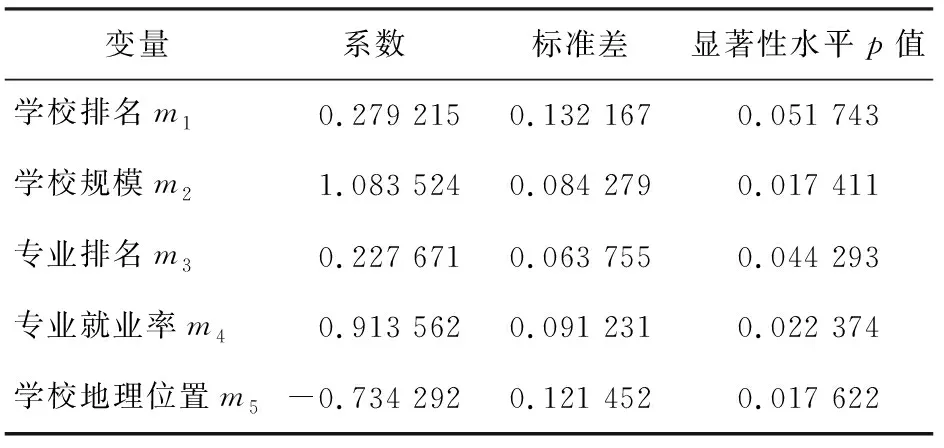
表9 分层线性模型的学校层面变量分析

从表中数据可以看出，m1、m2、m3和m4的系数均为正，m5的系数为负，表明学校排名、学校规模、专业排名和专业就业率对招生录取有正向影响，其中学校规模对录取的影响最大，系数达到了1.083 524，专业就业率次之，这可能是因为规模大的学校在专业设置及招生规模方面具有优势，所以录取率高、就业率好的专业，可能报考考生多，录取率也较高。相比之下，学校排名和专业排名对录取率影响并不大。学校地理位置对高校招生呈现负影响，系数为-0.734 293。当学校地理位置量化数值越大，录取率越不理想，表明学生在择校时更倾向于大城市。

从显著性来看，学校规模、专业就业率和学校地理位置对招生录取的影响更加显著，特别是学校规模和地理位置，p值均小于0.018。学校排名对招生录取的影响敏感度最低。

4 结语

本文中将FP-growth算法与分层线性模型运用于高校招生数据挖掘，结果表明：FP-growth算法能够较好地获得大置信区间的报到率数据，得到影响报到率的相关因素；采用分层线性模型，可以从学生层面和学校层面进行因素定量分析，获得影响招生录取的显著程度。后续研究将对分层线性模型的招生数据挖掘效果进行有效评价，通过科学评价方法不断完善数据挖掘模型，不断提高招生数据挖掘的有效性和准确性。