基于混合变异GOA优化极大似然的DOA估计研究

陈 婷， 白艳萍

（中北大学理学院，太原 030051）

阵列信号处理是信号处理的一个重要分支，目的是对阵列接收信号进行处理，增强所需有用信号，抑制无用的干扰和噪声，并提取有用的信号特征及信号所包含的信息［1］. 阵列信号处理研究的主要问题有以下几个方面：波束形成技术、空间谱估计、信号源定位和信源分离［2］. 其中，空间谱估计就是对空间信号波达方向的分布进行超分辨估计. 波达方向估计（DOA）不仅是许多军事和民用应用的一个过程，更是某些设备的基本功能，例如声呐和鱼雷. 对于这些设备来说，DOA估计的精度和速度会直接影响设备的性能，因此，如何改良DOA估计的精度和速度成为国内外当前研究的重点.

如何预估波达方向角，解决思路主要有以下两种：一是建立纯数学模型，通过大量计算得到结果，如传统的多重信号分类算法［3］（MUSIC）、旋转不变子空间算法［4］（ESPRIT）、极大似然算法［5］（ML）等；二是采用智能学习进行DOA估计，如BP神经网络［6］，径向基神经网络［7］等. 大多数DOA估计方法都需要对数据协方差矩阵进行特征分解，并且都有一定阈值限制，在低信噪比和少快拍数下，ML方法优于MUSIC方法和ESPRIT方法，所以我们选用ML方法进行主要讨论研究.

极大似然估计（ML）方法是子空间拟合类算法中的一种，但是由于其非线性的方向估计似然函数，导致在求解最优解时需进行多维搜索，运算量较大［8-9］. 近年来，基于仿生学的智能算法得到了快速的发展和广泛的应用，不少研究人员尝试使用这些智能优化算法来解决ML-DOA估计中的非线性搜索问题，例如比较经典的粒子群优化算法（PSO）［10-11］、烟花算法（FWA）［12-13］以及人工蜂群算法（ABC）［14-15］，另外还有近些年提出的正余弦优化算法（SCA）［16］、松鼠搜索算法（SSA）［17］以及人群搜索算法（SOA）［18］等. 蝗虫优化算法（GOA）［19-20］是Saremi等人受蝗虫捕食过程中种群行为的启发，在2016年提出的一种新型启发式智能优化算法. GOA优化算法简单便捷，计算复杂度较低，具有较高的收敛速度. 近年来，为了提高GOA优化算法的性能，众多专家学者对此做了大量研究工作. 本文采用改进的蝗虫优化算法对极大似然估计方法进行改进，并且应用在信号波达方向角的预估方面，通过对不同优化算法的迭代时间、对信噪比泛化能力以及信源个数泛化能力的比较，判别混合变异GOA优化ML方法进行DOA估计的拟合效果和稳定性.

1 算法

本文选用的蝗虫优化算法（GOA）源于对大自然中蝗虫群体的捕食行为的模拟，不仅通过它当前的位置和全局最好的位置更新位置，而且还通过其他蝗虫的位置更新位置，所有个体都参与到优化过程中，搜索效率更高，但是存在陷入局部极值的问题. 为了解决智能优化算法易陷入局部最优的问题，在这里引入重心反向解和柯西变异算子的概念. 重心反向解能够结合当前个体周围多个个体的经验，保持种群多样性. 柯西变异算子则具有更强的全局搜索能力，变异能力强，较易跳出局部最优解.

1.1 混合变异蝗虫优化算法

1）参数初始化，N，Max_iter，Cmax，Cmin，ub，lb 和dim. 其中：N 表示蝗虫种群个数；Max_iter 表示最大迭代次数；Cmax，Cmin用来计算求解c(·)的最值范围；lb 和ub 是计算蝗虫间距离的上下边界值；dim 表示维数.

2）初始化种群，根据适应度函数计算种群中每个蝗虫的目标函数值，按照目标函数值的大小进行排序，找出初始种群中的最优个体蝗虫.

3）开始循环，参数c(·)是缩小系数，目的是用来线性减少舒适空间，排斥空间和吸引空间. t 为蝗虫当前迭代次数，tmax即Max_iter 表示最大迭代次数，用

更新当前个体位置. 其中s(·)定义为一个函数表示为蝗虫间的社会作用力，

其中：f 表示吸引力的强度；l 是有吸引力的大小范围，此文中l=1.5，f=0.5，dij(t)取值范围为[1 ,4] .

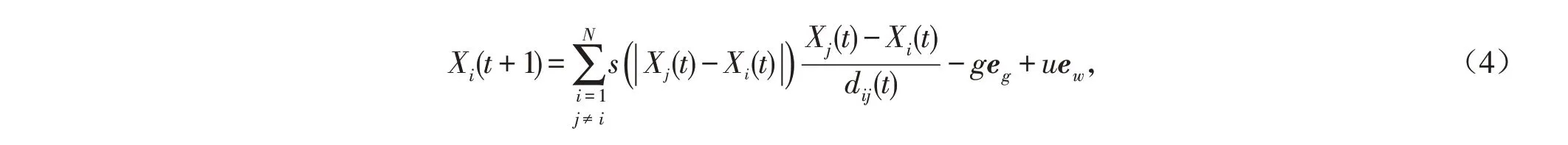
其中：N 代表蝗虫的数量，g 是引力常数，eg表示朝向地心的一个单位矢量，u 表示空气漂移常量，ew表示与风力方向相同的单位矢量. 幼年的蝗虫没有翅膀，因此它们主要的动力来源于风对蝗虫的作用力.

5）用下式求出更新后蝗虫的位置：

其中：k 表示一个[0,1]之间的随机数；M 是蝗虫种群位置的一个重心；R1是[0,1]之间的随机数；η 是用来控制柯西分布变异强度的一个常数；Xnow表示当前蝗虫个体的位置；Xnew表示更新后蝗虫个体的位置.

标准柯西分布函数形式如下：

Cauchy(0,1)是l=1时的标准柯西随机分布.

根据（5）式对当前个体的位置进行混合变异，得到跳出局部最优的搜索点，对这些搜索点代入到目标函数中进行计算，与当前最优个体进行比较，如果目标函数值优于当前最优个体的函数值，则进行位置的更新.

6）重新安置超过搜索边界的个体，计算所有个体的目标函数值，直至达到最大循环次数.

7）判断t 是否达到Max_iter，若是，则算法结束，同时输出T arg etposition 和T arg etfitness；若不是，令t=t+1，转向步骤3）继续执行.

1.2 基于混合变异GOA优化极大似然的DOA估计

在ML算法中，所得信号的似然函数被定义为含有未知参数的条件概率密度函数，通过选定未知的参数使得似然函数最大化. 由于求解过程需要多维搜索，运算量较大，所以引入混合变异GOA优化算法，能够在保证预估精度下有效加快搜索速度（图1）.

2 波达方向估计

2.1 非相干信号源下仿真实验

2.1.1 不同优化算法双信号预测角度 本文通过Matlab验证所提算法的可行性. 仿真条件：均匀的8元天线阵列，两个非相干的正弦信号作为信号源，信噪比为10 dB，快拍数为1000，阵元间距为半波长. 入射角度为［30°，50°］，每个优化算法小循环50次，主循环100次，对比其他四种不同优化算法（蝗虫优化算法（GOA）、人群搜索算法（SOA）、松鼠优化算法（SSA）、正余弦优化算法（SCA）DOA估计角度.

图2是五种优化算法进行DOA估计的角度对比图. 在100次主循环迭代过程中，信源1是30°，信源2是50°，GOA、SOA、SSA、SCA四种优化方法的输出DOA估计角度都有不同程度的波峰波谷，而混合变异GOA输出估计角度曲线在输入角度附近轻微浮动，更加接近于真实值，可以得出混合变异GOA方法优化的极大似然估计效果要优于另四种优化方法的优化效果，混合变异GOA优化极大似然的DOA估计角度更加精准，稳定性更高.

图1 基于混合变异GOA优化极大似然的DOA估计算法流程图Fig.1 Flow chart of DOA estimation algorithm based on mixed mutation GOA optimization maximum likelihood

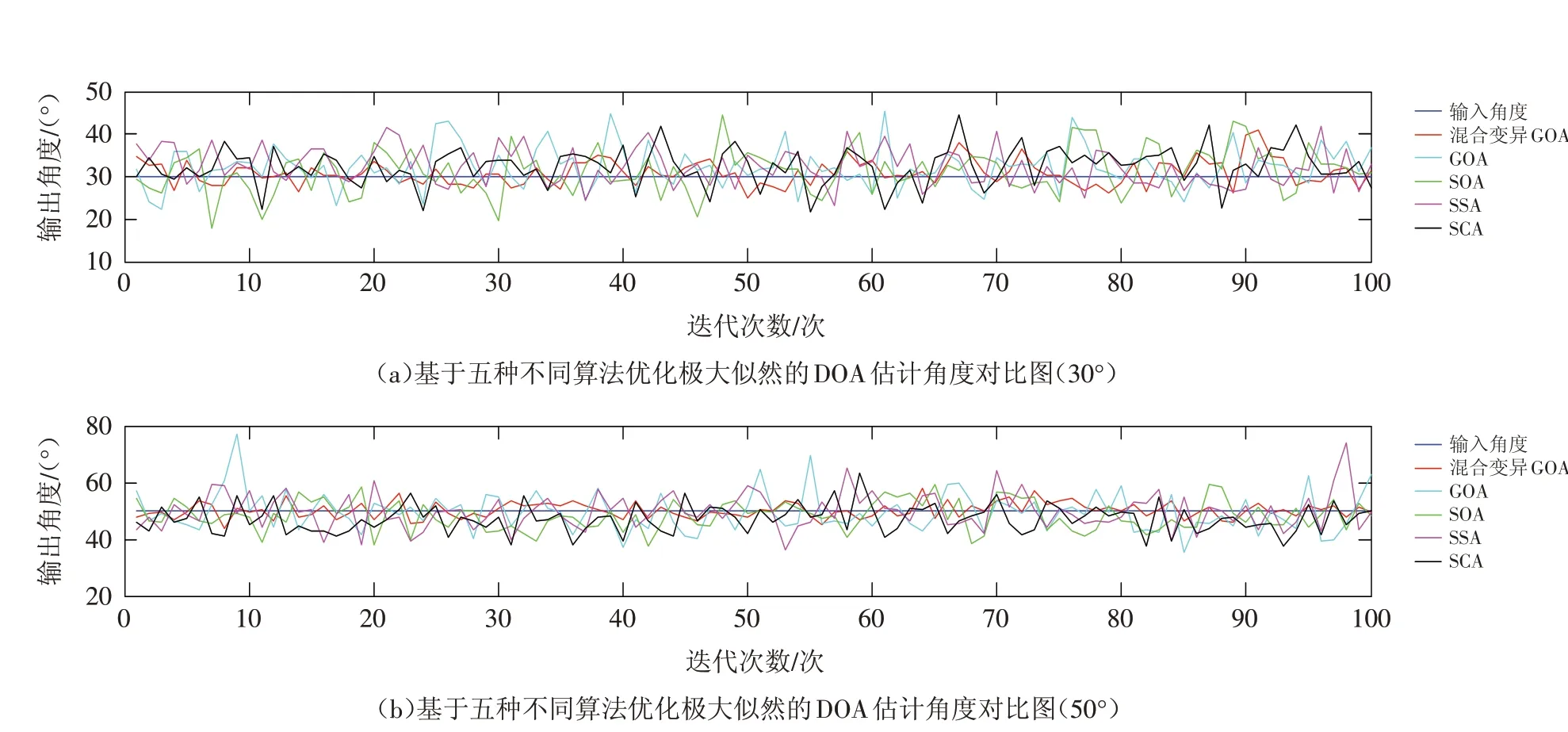
图2 双信号源的输出DOA估计角度Fig.2 DOA estimation angles of outputs of dual signal sources

图3是双信号源的输出DOA估计角度误差图，我们以输入角度和输出角度的误差值作为衡量指标. 通过图3可以看出，混合变异GOA方法优化极大似然的DOA估计角度误差曲线介于另外四种方法优化极大似然的DOA估计角度误差曲线之间，在0°曲线附近上下波动，而GOA、SOA、SSA、SCA四种优化方法的DOA估计角度误差都有不同程度的波峰波谷，可以得出混合变异GOA优化极大似然的DOA估计测角误差更小，拟合优度更好.

2.1.2 不同优化算法的DOA估计评价指标对比 仿真条件同仿真实验1，本实验选用均方误差（MSE）、均方根误差（RMSE）和平均绝对误差（MAE）作为衡量算法的指标.

均方误差（MSE）是衡量“平均误差”的一种较方便的方法，表示此时观测值与估计值之间的偏差，其计算公式为：

图3 双信号源的输出DOA估计角度误差Fig.3 DOA estimation angle errors of outputs of double signal sources

均方根误差（RMSE）是均方误差的算术平方根. 在实际测量中，观测次数总是有限的，真值只能用最可信赖（最佳）值来代替，均方根误差对一组测量中的特大或特小误差反应非常敏感，所以，均方根误差能够很好地反映出测量的精密度，其计算公式为：

平均绝对误差（MAE）是绝对误差的平均值，能更好地反映预测值误差的实际情况，其计算公式为：

式中：yn为第n 次实际输出值；y^n 为第n 次的网络输出值.

分别将混合变异GOA-ML、GOA-ML、SOA-ML、SSA-ML 和SCA-ML 的MSE 值、RMSE 值和MAE 值进行对比，见表1.

表1 基于五种不同算法优化极大似然的DOA估计评价指标Tab.1 DOA estimation evaluation indexes optimized based on five different algorithms for maximum likelihood

通过表1实验数据可以观察到，混合变异GOA-ML预估效果相比另外四种GOA-ML、SOA-ML、SSA-ML、SCA-ML 要更加精准，在100 次Monte-Carlo 仿真实验中，DOA 估计的MSE 值、RMSE 值和MAE 值都是这五种优化算法中最小的，说明通过混合变异GOA 优化算法改进后的极大似然估计方法拟合优度更好，稳定性较高.

2.1.3 不同优化算法迭代所需时间对比 仿真条件同仿真实验1，我们依次将混合变异GOA-ML、GOA-ML、SOA-ML、SSA-ML和SCA-ML的迭代50次，迭代100次，迭代150次，迭代200次的运行时间进行记录，见表2.

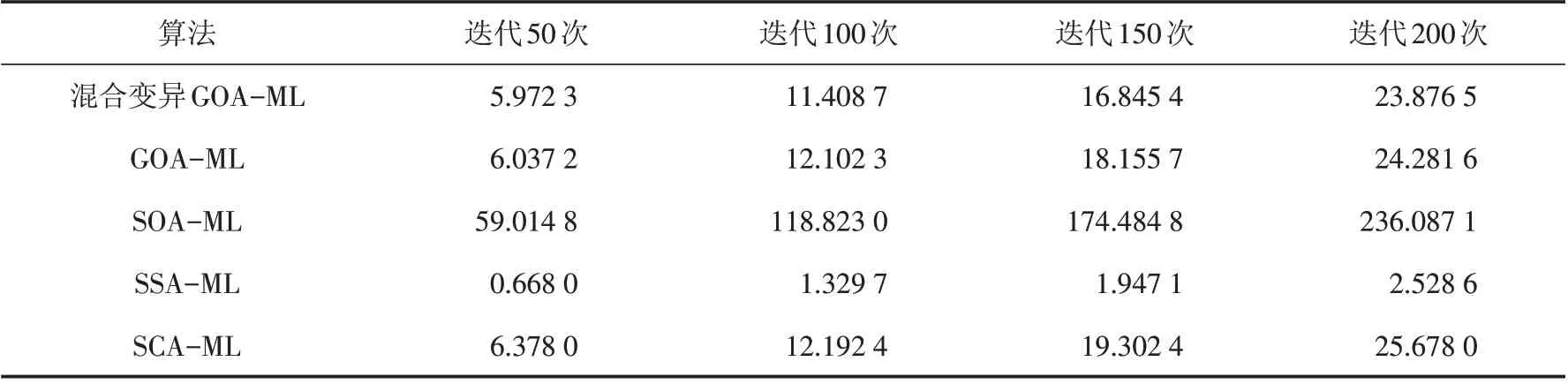
表2 不同优化算法迭代时间所需时间Tab.2 Iteration times required by different optimization algorithms 单位：s

通过表2结果可知，在其他条件相同时，从运算时间来看，SOA-ML算法的运行时间是最长的，SSA-ML算法的运行时间是最少的，造成这两种优化算法迭代运行时间如此大的差距原因是Matlab 是针对矩阵进行运算的一个软件，在SOA-ML优化算法中，主要迭代过程都是针对矩阵进行的，所以导致运行时间相对较长，而在SSA-ML优化算法中，迭代公式相对简单，所以运行时间最短. 在保证预估精度的情况下，本文提出的混合变异GOA-ML优化算法在运行时间方面也是仅次于SSA-ML算法，具有较强竞争力.

2.1.4 不同优化算法对信噪比的泛化能力 仿真条件：阵元数为8，信源数为2，信噪比为-15 dB、-10 dB、-5 dB、0 dB、5 dB、10 dB、15 dB，采样点个数100，这次将两个独立的窄带信号通过［30°，50°］两个方向入射到阵列中，利用混合变异GOA-ML算法、GOA-ML算法、SOA-ML算法、SSA-ML算法和SCA-ML算法依次进行矢量水听器的DOA估计，迭代次数100次，观察不同信噪比下，基于不同优化算法下极大似然估计的DOA估计的RMSE值，见表3.

表3 不同信噪比下的DOA估计误差Tab.3 DOA estimation errors under different SNRS

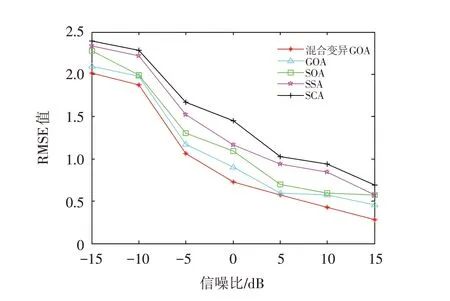
图4 不同信噪比下的DOA估计误差Fig.4 DOA estimation errors under different SNR

通过图4和表3结果可知，在信噪比-15 dB到15 dB之间，基于五种不同优化算法下极大似然的DOA估计RMSE 值都呈现减小的趋势，说明使用智能算法优化后DOA 估计效果更加精确，并且混合变异GOA-ML的DOA 估计RMSE值在-15 dB到15 dB之间要低于GOA-ML、SOA-ML、SSA-ML、SCA-ML 四种优化算法的RMSE值，可见经过混合变异GOA-ML进行DOA估计后的测向精度在逐步增强，测角误差更小，对信噪比的泛化能力更高.

2.1.5 不同优化算法对信源个数的泛化能力 智能优化算法的优化性能与适应度函数的维数有关，在ML-DOA 估计中，极大似然函数的维数就是信号源的个数，为此进行DOA 估计的RMSE 值相对于信号源数量的仿真实验.

仿真条件：阵元数为8，信源数依次为2、4、6、8、10、12、14，信噪比为10 dB，采样点个数100，利用混合变异GOA-ML 算法、GOA-ML 算法、SOA-ML 算法、SSA-ML 算法和SCA-ML 算法依次进行矢量水听器的DOA估计，迭代次数100次，观察不同信源个数下，基于不同优化算法下极大似然估计的DOA估计的RMSE值，见表4.

表4 不同信源个数下的DOA估计误差Tab.4 DOA estimation errors under different numbers of sources

图5 不同信源个数下的DOA估计误差Fig.5 DOA estimation errors under different numbers of sources

通过图5和表4结果可知，在当前仿真条件下，随着信号源个数的增多，RMSE值也相应增大，说明信号源个数较少的时候DOA 估计精度较好. 从这五种算法来说，在相同信源个数，相同仿真条件下，混合变异GOA-ML 的DOA 估计RMSE 值要小于GOA-ML、SOA-ML、SSA-ML、SCA-ML 四种优化算法的DOA 估计RMSE 值，其次是GOA-ML 和SOA-ML 方法，说明混合变异GOA-ML 的DOA 估计在不同信源个数下都具有较大优势.

2.2 相干信号源下仿真实验

由于传播环境的复杂性，入射到阵列的信号中往往有相干信号源存在，在DOA估计研究中，相干信号源干扰会造成目标定位错误. 此实验我们主要验证在相干信号源下，本文提出的混合变异GOA-ML模型的有效性.

仿真条件：均匀的8元阵列，两个相干的信号源，入射角度为［10°，60°］，信噪比为10 dB，快拍数为500，阵元间距为半波长. 我们选择传统的MUSIC方法、ESPRIT方法、ML方法、GOA-ML方法以及本文提出的混合变异GOA-ML方法依次仿真. 图6是MUSIC方法的输出DOA估计角度，可以看出波峰位置的坐标信息.表5是三种方法的DOA估计效果对比，选择相对误差作为衡量指标. 一般来说，相对误差更能反映测量的可信程度.

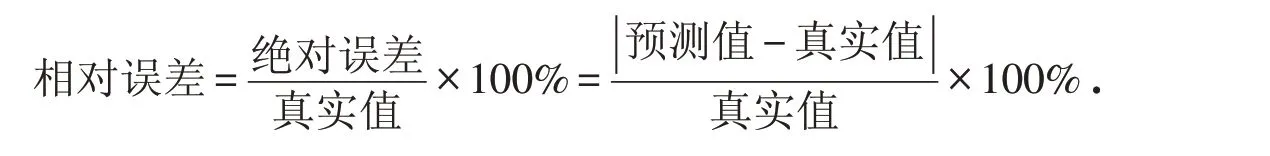
在众多性能优良的高分辨DOA估计算法中，MUSIC算法最为经典，它在空域内进行谱峰搜索求出信源来向. 相比于另外两种传统算法来说，MUSIC算法运算量要小很多，但是在相干信号下，传统的MUSIC算法已经不能有效地分辨信号的DOA. 通过图6也可以看出，估计的谱峰最大值对应的目标源信号入射角度分别为13°和59.5°，同时也存在其他一些小的波峰会对最终的结论造成干扰.

图6 MUSIC的输出DOA估计角度Fig.6 DOA estimation angles of MUSIC output

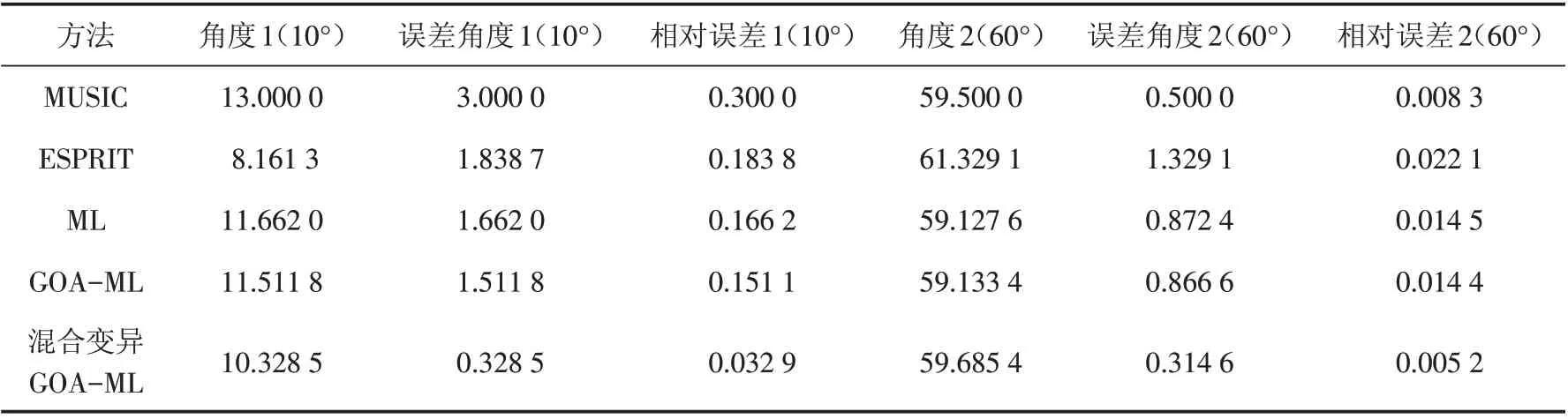
表5 相干信号下各类方法DOA估计效果对比Tab.5 Comparison of DOA estimation effects of various methods under coherent signals

在相同仿真条件下，观察表5结果，比较传统方法即MUSIC、ESPRIT和ML，ML-DOA对于角度1的估计更为准确，对于角度2 的估计则优于ESPRIT-DOA，略次于MUSIC-ML. 综合两个输入角度的相对误差来看，ML-DOA在相干信号下具有更强的竞争力. 我们进一步优化传统的ML方法，得到了GOA-ML-DOA 方法和混合变异GOA-ML-DOA 方法，在相同仿真条件下进行实验，可知相干信号源下，本文提出的混合变异GOA-ML方法的相对误差最小，所以在DOA估计精度有了很大的提高.

3 结果

通过大量仿真对比实验，我们观察到本文提出的混合变异GOA-ML 方法比其他优化算法的拟合优度要好，稳定性较高，能够保证估计值与输入值误差在±1°之内. 在保证预估精度的前提下，运行时间也具有较强的竞争力，对信噪比的泛化能力也比较强. 在实际生活中，往往存在的是相干信号源，因此我们讨论了在相干信号源下的DOA 估计效果. 通过仿真实验可知，在相干信号下，相较于传统的MUSIC 算法、ESPRIT 算法、ML 算法来说，混合变异GOA-ML 方法的相对误差最小，应用范围更广，更适用于处理相干信号的问题中.

4 结语

本文提出了一种基于混合变异GOA优化极大似然的新的DOA估计方法，该方法可以有效地提高DOA估计精度. GOA优化算法是一种不仅根据个体当前位置，还要根据和其他个体之间距离更新位置的智能群体优化算法，能够使更新位置更具有全局性，其中引入了柯西变异算子和重心反向解，不仅改善了极大似然估计的搜索效率，也避免了GOA优化算法容易陷入局部最优的问题，并在非相干信号和相干信号两大类仿真实验下，验证了改进方法具有更高的估计精度和更好的泛化能力，并且在保证其他性能良好的情况下，算法运行时间方面有较强优势，相对于其他方法的性能有一定的提升.