基于双向长短期记忆网络的流体高精度识别新方法
周雪晴, 张占松, 朱林奇, 张超谟
(1.长江大学油气资源与勘探技术教育部重点实验室,湖北武汉 430100;2.长江大学地球物理与石油资源学院,湖北武汉 430100; 3.中国科学院深海科学与工程研究所,海南三亚 572000;4.青岛海洋科学与技术国家实验室海洋地质过程与环境功能实验室,山东青岛 266237)
碳酸盐岩储层由于储集空间类型多样、储层性质复杂、非均质性极强,导致不同的流体性质在测井曲线上的响应不明显,这给气、水识别工作带来极大的困难[1-2]。大量学者基于测井曲线响应特征及其衍生的各种岩石物理参数开展了相关的研究工作,包括交会图法[3]、曲线重叠法、数理统计法[4],利用特殊测井(包括电成像测井、阵列声波测井、核磁测井等)计算各类岩石物理参数及流体表征参数的流体识别方法[5]等。然而,受成本限制,特殊测井难以在大多数井中测量,且在大多老井中未采集。因此基于常规测井曲线的流体识别仍然是研究热点且存在很大挑战[6]。目前针对流体分布复杂的储层,多基于机器学习类方法进行流体识别,例如使用支持向量机[7],模糊逻辑模型、决策树类、神经网络及其衍生方法等[8]。近年来,随着深度学习的兴起,其强特征提取及非线性逼近能力在各行各业得到广泛的研究及应用,成为近年研究的热点内容之一[9-11]。目前,深度学习在储层参数建模、储层识别、孔隙特征预测、裂缝识别[12]等研究中取得较好的应用效果。但是,在流体识别方面,多应用传统的全连接神经网络,建立的映射多为点对点映射,导致在强非均质性储层中应用效果不佳。笔者应用深度学习中先进的循环神经网络-双向长短期记忆网络(Bi-LSTM)建立流体识别模型,充分发挥研究区测井曲线与流体类型之间的非线性及连续性特征,并对比长短期记忆网络及3类经典机器学习算法预测效果。
1 基于Bi-LSTM的流体识别方法原理
1.1 长短期记忆网络
长短期记忆网络(LSTM)是循环神经网络(RNN)的改进算法之一[13],其保留了RNN处理时序数据的优势。通过门机制将短期记忆与长期记忆结合起来,解决RNN 只能记忆短期的历史输入信息无法有效解决长期记忆的问题,又在一定程度上解决了梯度消失和梯度爆炸的问题。LSTM保留了RNN的链式形式,由一系列递归连接的记忆区块的子网络构成,其中关键结构即交互层中的3个门层[14],即输入门、输出门、遗忘门。遗忘门决定着细胞状态Ct-1对Ct的影响,输入门主要是xt对Ct的影响,主要是将新信息添加到当前步骤的细胞状态中。输出门主要是Ct对ht的影响,对应的数学表达式如下:
ft=σ(Wfxt+Wfht-1+bf),
(1)
it=σ(Wixt+Wiht-1+bi),
(2)
Ct=ft⊙Ct-1+it⊙(tanh(Wgxt+Wght-1+bg)),
(3)
ot=σ(Woxt+Woht-1+bo),
(4)
ht=ot⊙tanh(Ct).
(5)
式中,σ为sigmoid函数;ft、Wf、bf分别为遗忘门在t时刻的状态、权值及偏置;it、Wi、bi分别为输入门在t时刻的状态、权值及偏置;ot、Wo、bo分别为输出门在t时刻的状态、权值及偏置;Wg、bg为细胞状态在t时刻的权值及偏置;⊙为Hadamard积;xt和ht为t时刻的输入及输出。
利用以上结构,在各个时间部t都可以得到对应的隐层状态序列,根据输出样本维数,变换得到最终的输出结果。但是由于LSTM只能按从前到后的顺序来处理数据,无法加入后面数据信息的影响,使用过程中仍存在一定的不足。
1.2 双向-长短期记忆网络
为了将后面信息的影响加入到模型中,提高模型的精度及效果,本文中使用双向-长短期记忆网络(Bi-LSTM)[15],该网络由一个前向LSTM模型与后向LSTM模型连接组成,作为时序相反的两个LSTM网络,前向LSTM 可以获取输入序列的上部储层段的信息,后向LSTM 可以获取输入序列的下部储层段的信息,即该模型能从前、后2方面充分获取上下储层段的信息,提高模型效果。
图1为Bi-LSTM模型示意图(图中,yt为t时刻Bi-LSTM输出)。为便于理解及表达Bi-LSTM模型,分别将前向LSTM模型的输出表示为hat,后向LSTM模型的输出为hbt,W1~W6为权值矩阵,可以用以下公式表示:
hat=f(W1xt+W2hat-1),
(6)
hbt=f(W3xt+W5hbt-1),
(7)
(8)
其中concat表示向量拼接,即利用公式(8)串联起前向LSTM及后向LSTM模型的隐藏层向量,将得到的最终隐藏层向量输入到softmax函数,得到Bi-LSTM模型的最终预测结果。
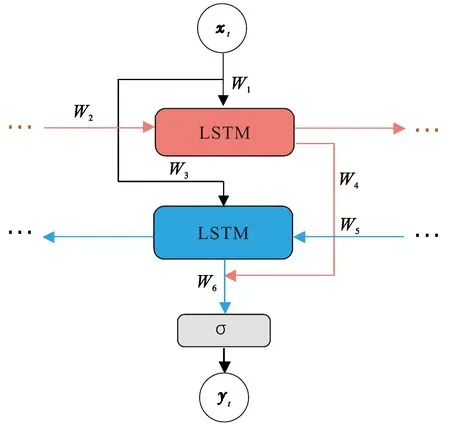
图1 Bi-LSTM模型示意图Fig.1 Bi-LSTM network
1.3 基于Bi-LSTM的流体识别框架
在储层纵向非均质性较强的情况,地下某一深度对应的测井曲线响应值会受到上下储层性质变化的影响。将Bi-LSTM网络思想引入到储层流体识别中,类比于时间序列中特征向量随时间的变化,测井曲线响应值即随着深度而变化,构建出测井序列作为流体识别模型的输入,利用Bi-LSTM模型的记忆能力,构建出考虑测井曲线的变化趋势及上下数据的相关关系的流体识别模型,来有效克服储层纵向非均质性带来的影响。本文中搭建的流体识别模型主要由6部分组成(图2),包括预处理层、输入层、Bi-LSTM层、全连接层、softmax层及输出层。
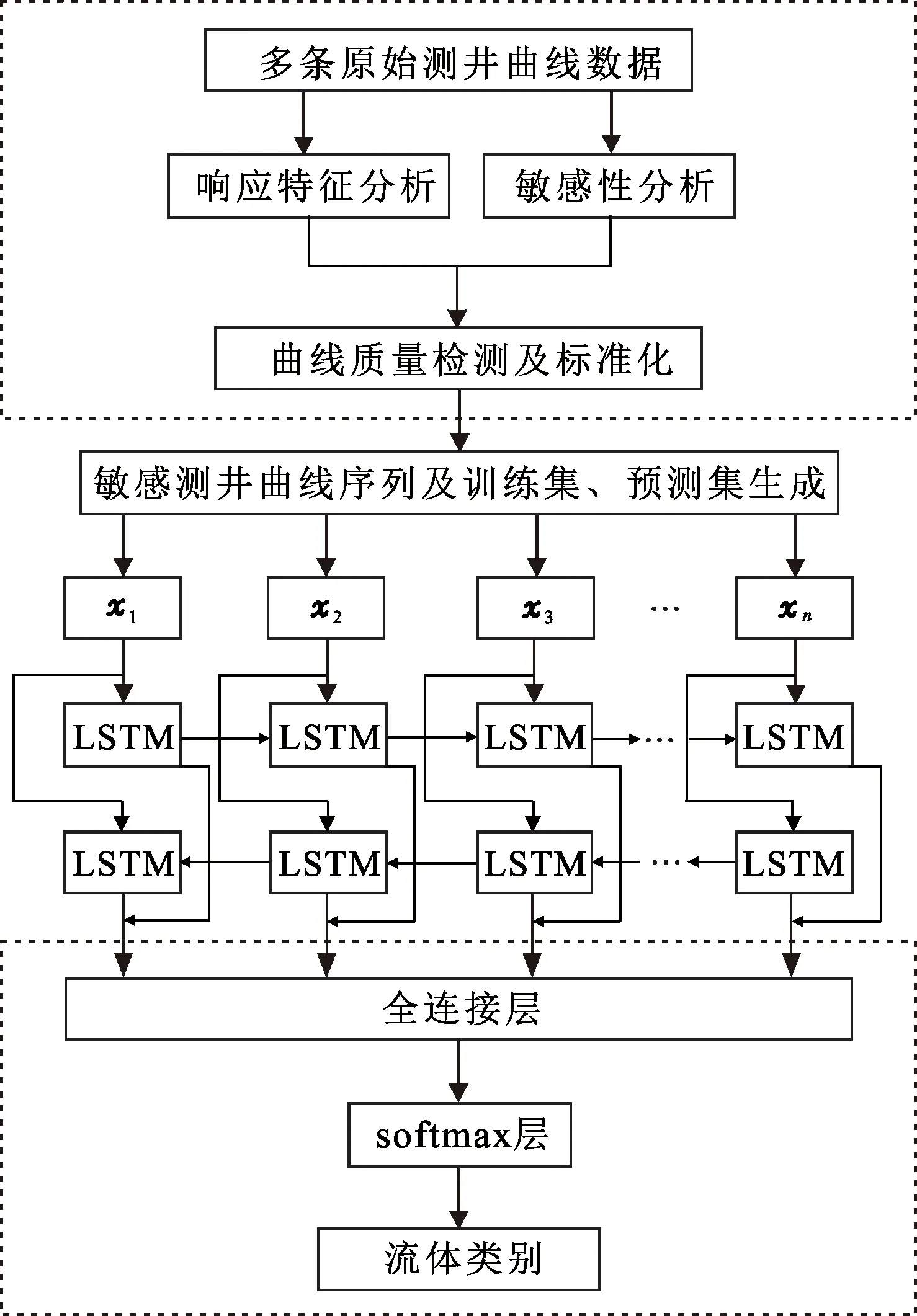
图2 基于Bi-LSTM流体识别模型框架Fig.2 Fluid identification framework of Bi-LSTM neural network
其中预处理层包含流体敏感曲线的选取、质量检测及标准化,保证了模型输入数据的准确性;输入层将常规点对点映射变为序列对点映射,把深度段的连续测井曲线值看作序列数据,形成输入层;Bi-LSTM层是网络的核心部分,该层的上层/下层输出将用作下一层/上一层的输入(前向、后向LSTM网络模型相接),起到有效利用储层上下层信息的作用。经过Bi-LSTM层的多次迭代求解,直到模型收敛,结果作为输入向量进入全连接层,其输出结果经过softmax层后输出为流体类别,形成最终的流体识别模型。
2 马家沟组中组合流体识别难点
研究区块位于鄂尔多斯盆地伊陕斜坡中北部,是含气富集区也是目前勘探的热点地区,由于受构造运动、储集空间类型多样性、天然气成因及来源的差异性的影响,储层非均质性较强,高产井分布范围有限,气水关系复杂且存在高阻出水现象[16]。根据马家沟组450块岩样的岩心物性分析资料,统计分析了孔隙度分布(图3(a))。通过试验结果发现,孔隙度主要分布在0~6%,平均为3.15%。根据岩石薄片资料,研究区储集空间类型多样(图3(b)),主要发育微裂缝、晶间孔和溶孔3种储集空间类型。概括来说,研究区储层致密、具有孔隙空间小、储集空间类型复杂多样等特点,测井曲线受到储集空间类型的影响,流体信号弱,测井响应特征复杂,气水层测井解释难度加大。
为分析不同流体的响应特征,首先,根据研究区试气资料,梳理出6种流体类型,分别为气层、差气层、气水同层、含气水层、水层及干层。其次,为充分放大气层响应特征,提高流体识别精度,根据不同测井的测量原理及对流体的响应特征[17],尝试计算了5个衍生参数,分别为密度孔隙度φD、声波孔隙度φS、三孔隙度差值C、三孔隙度比值B、基于多矿物模型孔隙度φ,计算公式为
(9)
(10)
φN=IH,
(11)
C=φD+φS-2φN,
(12)
(13)
式中,ρ为岩性密度;ρma为石灰岩骨架密度,取2.71 g/cm3;ρf为流体密度,取1 g/cm3;Δtma为石灰岩骨架声波时差,取156 μs/m;Δtf为流体的声波时差,取620 μs/m;IH为含氢指数,等于测量的中子响应值。
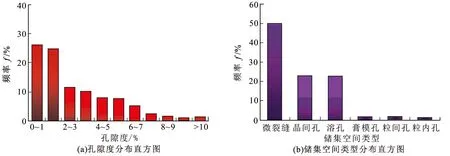
图3 研究区孔隙度及储集空间类型分布直方图Fig.3 Histogram of porosity and pore type distribution
图4是研究区7条常规测井曲线及5个衍生参数对应的不同性质流体响应特征折线图。从7条测井曲线响应值可以看出,对于不同性质的流体,测井响应特征差异不大,总结为以下几个方面:①对流体敏感的电阻率曲线在研究区不同性质的流体识别中,难以直接发挥作用,研究区存在部分高阻水层现象,即水层的电阻率接近甚至高于气层电阻率;②从物性曲线(密度ρ、中子φCNL、声波Δt)响应值来看,水层及气层物性均较好;③部分干层的测井响应为气层特征;④含气水层及气水同层测井响应变化较大,响应特征与气层、差气层及水层交叠,识别难度较大。

图4 研究区不同性质流体典型测井响应折线图Fig.4 Fold Line chart of logging responses of different fluid in study area
根据图4衍生参数在不同性质流体中的响应特征分析,计算得到的衍生参数对研究区气层响应特征的放大能力有限,孔隙度φ及孔隙度差值C可一定程度上区分某一类流体性质,但采用单一参数或常规测井曲线均难以识别研究区流体性质。总结不同流体的响应特征,建立的流体识别线性模型预测精度为61.54%,难以满足生产要求。
在研究区复杂孔隙系统、强储层非均质性的情况下,有必要在确定流体敏感曲线后,建立能充分挖掘储层信息、考虑强非均质性影响的流体识别模型。
3 研究区块模型建立与分析
3.1 敏感曲线选取及特征分析
根据对常规测井曲线及衍生曲线在不同性质流体中的响应特征分析,虽然难以简单利用测井曲线响应值有效识别流体性质,但不同曲线的响应值对不同类型的流体有不同程度的区分,即存在一定的类间差异。例如,密度及深侧向电阻率曲线RLLD对干层敏感,中子、声波、C、φD、φS及φ曲线对差气层敏感,自然伽马GR、浅侧向电阻率曲线RLLS对气水同层敏感。因此筛选确定出10条敏感曲线,包括6条常规测井曲线、4条衍生曲线。
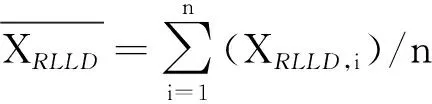

(14)
式中,n为每列的长度;r(RLLD,ρ)为曲线RLLD与ρ的相关系数范围为-1到1,-1表示完全负相关,而值为1表示完全正相关,值为0表示列之间没有关联。
图5为10条曲线间的相关性检验结果,从图中可以看出,由于衍生曲线中的φD、φS为ρ、Δt曲线直接通过线性变换所得,完全线性相关;同样,C由ρ、Δt、φCNL曲线计算而来,与ρ、Δt存在强相关关系;此外,深浅电阻率之间存在正相关关系,而φ与各条原始常规测井曲线之间不存在高度共线性关系。综合10条敏感曲线相似性分析结果,去除高度共线性曲线,最终优选出以常规测井曲线为主的ρ、Δt、φCNL、φ、RLLD、GR 6条曲线输入组合及以衍生曲线为主的φ、C、φCNL、RLLD、GR 5条曲线输入组合来分别建立流体识别模型。由于输入组合不同时,后续训练样本及Bi-LSTM流体识别模型建立过程类似,为减少重复内容,训练样本建立及Bi-LSTM流体识别模型两部分以6条曲线输入组合为例论述。
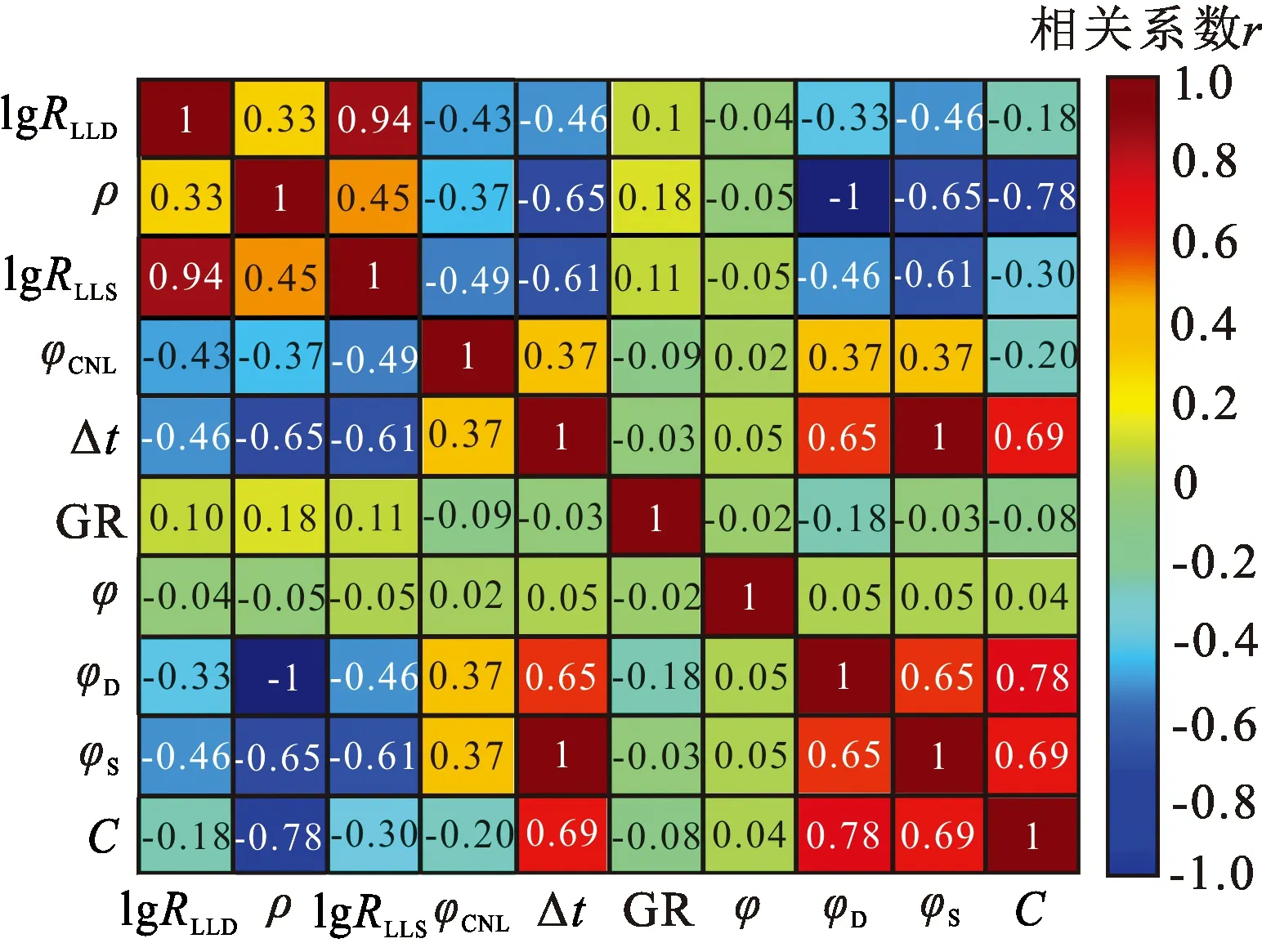
图5 测井曲线及衍生参数相关度热图Fig.5 Heat map of correlation of different logging curves and derivative parameters
3.2 训练样本建立
训练样本建立包括预处理及序列样本生成2部分。预处理包括测井曲线质量检测及曲线归一化。曲线质量检测剔除扩径严重、曲线失真井段,保证了数据的可靠性,曲线归一化消除各类参数量纲差异带来的影响,提高后续模型收敛速度及精度。
序列样本生成包括数据充填及序列提取。首先通过插值进行数据充填,使得生成的序列长度统一。其次,设置序列长度为8个采样(总长度为1 m)的滑动窗,自上而下对31 口井试气层段的测井数据进行提取,形成训练序列数据。根据研究区试气资料,一共生成681组有效深度序列数据,按照训练样本集与验证样本集7∶3的比例,随机抽取其中200组作为验证样本集,其余作为训练样本集。
3.3 基于Bi-LSTM流体识别模型
确定训练样本集以及验证集后,建立基于Bi-LSTM网络的流体识别模型。为了防止过拟合,对Bi-LSTM层中的连接添加Dropout,即将神经网络结构中的隐藏层节点按照给定概率进行丢弃,增加了训练网络的多样化,提高模型的泛化能力。模型内部选用Adam算法,使用交叉熵损失函数,通过不断的迭代更新,观察损失函数变化,直到模型收敛停止,确定最终网络模型。由于循环神经网络的序列输入模式以及内部网络结构,使得网络本身的结构就比较深,所以无需设置过多的Bi-LSTM层。经过多次试验,设置2层Bi-LSTM层,1层全连接层,其他网络结构参数设置为:隐层神经元数100,最小批训练次数16。除此之外,针对学习率对网络的影响,采用动态学习率,将网络训练分为前期及后期两部分,网络训练前期采用较大学习率,随着模型的收敛,后期减小学习率,以使模型更好地收敛,初始学习率设置为0.01。计算机系统环境为Windows 10 64位系统,内存为32 GB,双处理器(Intel(R) Xeon(R) CPU ES-2660 v3 @ 2.60 GHz)。
图6为Bi-LSTM流体识别模型训练过程。从图中可以看出,随着网络的迭代更新,模型复杂度增加,训练样本误差渐渐减小的同时,验证集损失函数整体呈现为先快速下降,后逐渐收敛保持平稳的变化趋势,未出现损失函数值先下降后逐步升高的过拟合现象。模型在迭代到6 500次后,模型收敛,得到最终模型。
4 对比分析
根据敏感曲线选取及特征分析,确定两种不同的输入曲线组合,并分别建立基于Bi-LSTM流体识别模型,其中以常规测井曲线为主的ρ、Δt、φCNL、φ、RLLD、GR 6条曲线输入组合建立的流体识别模型判别精度为91.5%,以衍生曲线为主的φ、C、φCNL、RLLD、GR 5条曲线输入组合建立的流体识别模型判别精度为85.5%。根据两个模型的稳定性及精度,最终采用以ρ、Δt、φCNL、φ、RLLD、GR 6条曲线输入组合建立的Bi-LSTM流体识别模型。
为验证Bi-LSTM模型在测井流体识别问题中的优势,将图2中的Bi-LSTM层换为LSTM层,建立单向LSTM流体识别模型。为充分验证基于序列信息的流体识别模型的应用效果,对比分析包括Fisher判别、支持向量机SVM、贝叶斯3种经典机器学习方法的流体识别精度。此外,分析研究区多口井的流体识别结果与试气结论,从实际运用效果中验证模型的可靠性。为保证对比结果的可靠性,Fisher判别、支持向量机、贝叶斯均采用相同的建模样本集及预测样本集。其中贝叶斯判别采用朴素贝叶斯判别Naive Bayes,判别精确度见表1。从预测精度来看建立的5个非线性模型精度均高于前文中建立的流体识别线性模型,考虑测井序列信息的LSTM模型精度高于其他3种机器学习方法,凸显了一定的模型优势。
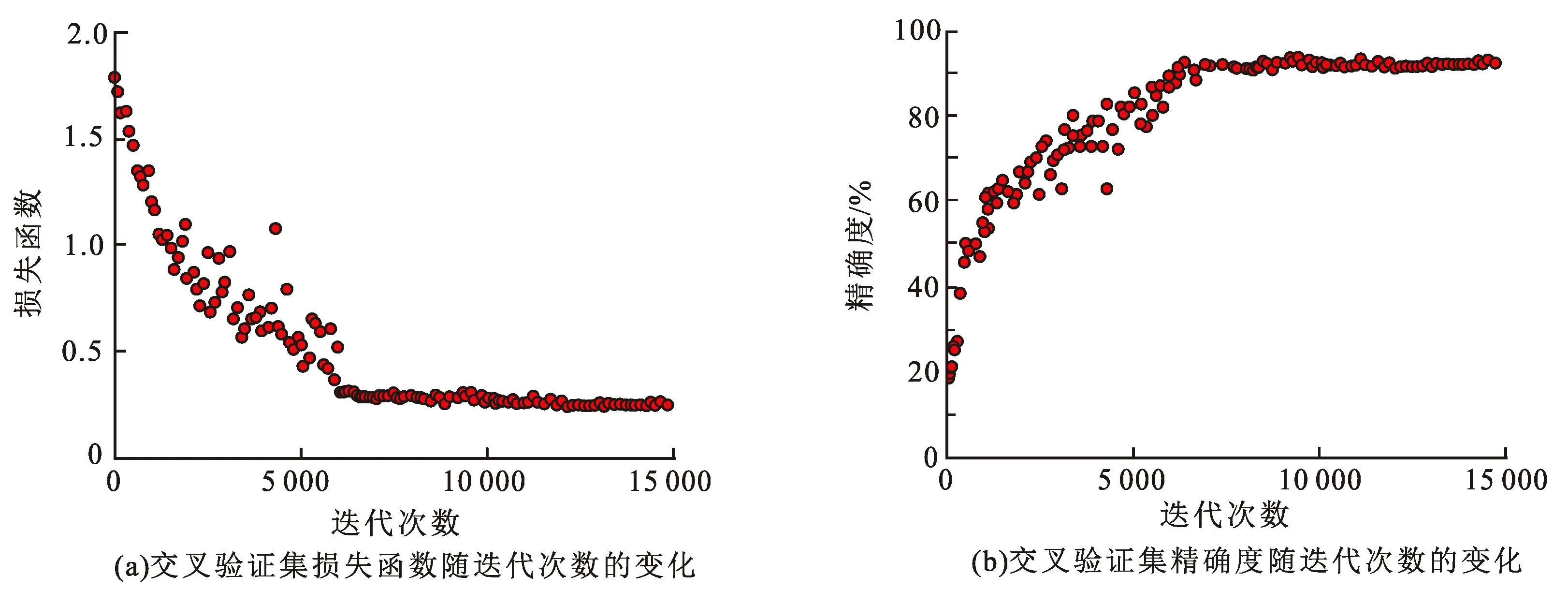
图6 交叉验证集损失函数及精确度随迭代次数的变化Fig.6 Cross validation set loss and accuracy change with number of iterations

表1 不同流体识别模型精度
将建立的Bi-LSTM流体识别模型及单向LSTM、Fisher判别、支持向量机、贝叶斯判别5个流体识别模型应用于研究区预测井中,图7为A井5种流体识别模型流体识别结果。其中3 612~3 614 m为测试层段,日产气5.43×104m3,试气结论为气层,是研究区典型气层。从测井曲线响应特征来看,测试层段物性较好,孔隙度分布范围在7%~9%,基于Bi-LSTM流体识别模型、LSTM流体识别模型及Fisher判别模型均可有效识别气层段,而Bayes模型及SVM模型的判别结果为水层,从识别结果来看,Bi-LSTM流体识别模型除精度优势外,表现出更高的模型稳定性。

图7 A井5种流体识别模型流体识别结果Fig.7 Fluid identification results of 5 fluid identification models in well A
图8为B井5种流体识别模型流体识别结果。3 696.5~3 698.5 m及3 702.5~3 705 m为测试层段,日产气0.084×104m3,日产水26 m3,试气结论为水层。从测井曲线响应特征来看,测试层段电阻率较高,上段深侧向电阻率均值约200 Ω·m,下段深侧向电阻率均值约400 Ω·m,是研究区典型的高阻水层。基于Bi-LSTM流体识别模型、LSTM模型、Bayes判别模型及SVM模型的判别结果为水层,Fisher判别模型在此处难以有效识别水层,判别结果为气水同层及差气层。从两口典型井的判别结果来看,经典机器学习算法的流体识别模型,在对气层及高阻水层的识别上,存在模型偏重,即Fisher判别模型偏重于将具备气层特征的储层识别为气层,Bayes判别模型及SVM模型的判别结果偏重为水层,并未真正挖掘到曲线与流体之间的关系,难以识别疑难层的流体性质。基于连续序列信息的Bi-LSTM/LSTM模型均能充分利用测井响应特征,其中Bi-LSTM流体识别模型精度及稳定性更强,更适用于强非均质性储层中的流体识别问题。

图8 B井5种流体识别模型流体识别结果Fig.8 Fluid identification results of 5 fluid identification models in well B
5 结束语
将Bi-LSTM网络思想引入储层流体识别中,充分利用Bi-LSTM模型的记忆能力,构建出考虑测井曲线的变化趋势及上下数据的相关关系的流体识别模型。模型的设计框架符合循环神经网络模型的设计原理,又充分考虑了测井流体识别问题的特殊性,最终建立了包括预处理层、输入层、Bi-LSTM层、全连接层、softmax层及输出层的6层网络,预处理层中的流体敏感曲线的选取、质量检测及标准化,确保了输入样本的正确性。模型中的Adam算法及超参数的选取,保证了模型在更新迭代中找到最优模型。该模型已在鄂尔多斯盆地马家沟组中应用,与其他4类算法预测结果的对比表明,基于Bi-LSTM的流体识别模型,能有效识别流体性质,提高流体识别符合率。基于Bi-LSTM流体识别模型有望改善复杂储层的流体识别和评价,为复杂储层流体识别提供新思路。

