高强钢组合Y形偏心支撑框架抗震性能混合试验研究

李腾飞，苏明周,2，隋 龑,2，赵 坤，张 琦，王路路

(1.西安建筑科技大学土木工程学院，陕西，西安710055；2.西安建筑科技大学结构工程与抗震教育部重点实验室，陕西，西安710055；3.中国联合工程有限公司第一工业设计研究院，浙江，杭州310052)

近年来，钢结构因其重量轻、强度高、塑性和韧性好、制造安装方便等特点，在建筑领域发挥着越来越重要的作用。偏心支撑钢框架作为一种典型的钢结构体系，兼有中心支撑结构和抗弯框架结构的优点。在罕遇地震作用下，地震能量通过消能梁段的塑性变形来耗散，而其他结构构件仍处于弹性阶段[1]。图1为三种典型的偏心支撑布置形式，分别是Y 形、K 形和D形偏心支撑。尽管Y形偏心支撑的侧向刚度相较于其他两种支撑形式略低，但由于其消能梁段位于框架梁外，因此可以单独设计梁段的截面尺寸和长度，以优化整个结构的性能。此外，在罕遇地震作用下，Y 形偏心支撑框架的塑性变形主要集中在梁段处，而框架梁和楼板的破坏最小，因此在地震后易于修复[2-3]。

图1 典型偏心支撑布置Fig.1 Typical layout of EBF

为了充分利用消能梁段的塑性变形，《建筑抗震设计规范》[4]采用对非耗能构件的内力进行了放大的方式，这往往导致框架梁柱的截面过大，限制了该种结构形式的应用，而本文所介绍的高强钢组合Y形偏心支撑框架便是为了解决这一问题而提出的，即消能梁段采用屈服点较低的普通钢材(如LYP225钢、Q235钢或Q345钢，名义屈服强度分别为225 MPa、235 MPa 和345 MPa)，框架梁、柱采用高强度钢材[5-6]。在罕遇地震作用下，消能梁段完全进入塑性状态以耗散能量，保证结构具有良好的塑性变形和耗能能力，而框架梁和框架柱仍处于弹性状态或部分发展塑性。同时，高强钢的采用可以有效地减小框架梁柱的截面，节约材料和降低成本。

尽管一些学者对Y 形偏心支撑框架结构进行了理论分析和试验研究[7-8]，但针对高强钢组合Y 形偏心支撑框架的研究相对较少。段留省等[9]对高强钢组合Y 形偏心支撑平面试件进行了单调和循环加载试验。王凤等[10]对一个3层高强钢组合Y 形偏心支撑框架进行了拟静力试验，分析了结构的承载能力、延性和破坏模式。然而，拟静力试验无法获得结构在真实地震波作用下的动态响应。连鸣等[11]对一个高强钢组合Y 形偏心支撑框架模型进行了振动台试验。根据相似比例的要求，振动台试验模型的质量通常超过了台面的承载能力，因此学者们采用增大输入加速度的方式来弥补模型的“欠质量”，然而这样的处理方式仍可能导致结构的动态响应(特别是与质量有关的惯性力)失真。

本文采用一种新型的子结构混合试验方法对高强钢组合Y 形偏心支撑框架的抗震性能进行深入研究。混合试验将子结构拟动力试验[12]与通用有限元软件相结合，取整体结构中的易损部分作为试验子结构进行实际试验，结构剩余部分作为数值子结构在有限元软件中进行模拟。混合试验弥补了拟静力试验和振动台试验存在的不足，具有很好的实际应用前景[13-16]。首先，以一个3层3跨的高强钢组合Y 形偏心支撑框架结构为原型，选取底层带有偏心支撑的框架部分作为试验子结构，其余部分作为数值子结构在OpenSees中进行模拟。然后采用子结构混合试验方法进行了一系列试验研究，根据试验结果，验证了子结构混合试验模型的有效性，并对混合试验模型的主要抗震性能指标进行了分析。

1 混合试验模型建立

1.1 原型结构设计

如图2(a)所示，原型结构为一个3层3跨的高强钢组合Y 形偏心支撑框架，结构层高为3600 mm，两个方向跨度为5650 mm，消能梁段长度为700 mm。选取模型底层带有偏心支撑的框架部分作为试验子结构进行实际试验，结构剩余部分作为数值子结构在有限元软件OpenSees中进行模拟，子结构之间的通信选择OpenFresco试验平台。考虑到试验场地、设备性能等限制，将原型结构按1∶2进行缩尺，缩尺后的结构层高为1800 mm，跨度为2825 mm，消能梁段长度为350 mm。框架梁、柱使用Q460钢材，支撑使用Q345钢材，消能梁段使用Q235钢材。构件的具体截面尺寸见表1。试验子结构的钢材材性试验结果见表2。试验模型各构件之间均采用焊接连接，其中消能梁段的上端与梁下翼缘焊接，下端与支撑端部焊接，焊条材料与耗能梁段钢材相适应(见图2(b))。

图2 试验模型示意图Fig.2 Test model

表1 构件截面参数Table 1 Cross sectional dimensions of members

1.2 数值子结构建模

OpenSees作为一款兼具计算效率和计算精度的有限元建模软件，越来越受到研究人员的关注，其最大特点是对用户的开放性，用户可以自定义添加各种新型材料本构，新型单元模块等。本次混合试验便使用OpenSees来进行数值子结构建模。

如图3所示，框架梁柱使用基于力的梁柱单元(force-based beam-column element)，截面使用可以考虑构件强非线性的纤维截面，材料使用可以考虑包辛格效应的Steel02本构模型。Steel02 的具体参数设置见表3，其中屈服强度fy和弹性模量E取为表2材性试验结果的平均值，应变硬化率b，曲线过渡段参数R0、cR1、cR2以及等向强化参数a1-a4均参考OpenSees用户手册[17]建议取值。支撑使用两端铰接的桁架单元(trusselement)。消能梁段的建模是数值子结构建模的关键，本文借鉴文献[18]中建立K 形偏心支撑的思想，使用零长度单元加剪切弹簧的方法来模拟整个消能梁段的剪切变形，其中剪切弹簧材料仍使用Steel02进行模拟，具体参数设置见表4。除了剪切弹簧的屈服剪力Vy对应Steel02的屈服强度fy，剪切线刚度K0对应Steel02的弹性模量E外，其余参数设置与表3一致。模型的整体质量矩阵M见下式：

图3 有限元模型示意图Fig.3 Finite element model

表2 钢材力学性能Table 2 Mechanical propertiesof steel

表3 Steel02参数设置Table 3 Parametersof Steel02

表4 剪切弹簧参数Table 4 Parametersof shear spring

1.3 试验子结构

1.3.1试验加载装置

如何模拟试验子结构真实的边界条件和加载条件一直是混合试验研究中的一个关键问题。本次混合试验所建立的试验子结构为一个由2 榀偏心支撑组成的单层空间钢框架模型，其边界处的自由度模拟即为4个框架柱顶沿不同方向的位移加载模拟。由于子结构边界处共存在6×4=24个自由度，无法使用作动器和千斤顶对所有自由度进行模拟，因此必须对子结构的边界加载做合理的简化。考虑到在水平地震作用下，框架结构在刚性楼板假定下具有良好的整体性，层高处边界节点的水平位移为其主自由度，因此我们仅考虑在竖向重力荷载作用下框架整体的平动自由度模拟。

如图4所示，为了实现试验子结构水平平动加载，参考OpenFresco试验平台提供的双作动器加载模式(two actuators experimental setup)，使用2个100 t MTS电液伺服作动器以及1个层高0.9 m的中心支撑钢框架来实现。一个作动器位于试验子结构层高处，另一个作动器位于加载段框架层高处。在加载的过程中，我们保证两个作动器位移同步且一致，并假设加载段的刚度相对试验子结构为无穷大(实际刚度比为6∶1)，即加载段在加载过程中不会发生变形，便可实现试验子结构边界处的纯平动加载。竖向加载装置主要包括千斤顶以及传递竖向荷载的分配梁。

1.3.2试验单元等效

图4 试验加载装置Fig.4 Loading equipment

为了实现试验子结构与数值子结构之间的数据通信，需要使用OpenFresco中提供的试验单元模块。试验单元是一种特殊的单元，它可以用来表示混合试验模型的试验子结构部分，其恢复力参数不是提前定义好的，而是通过试验时作动器实测得到的试件位移和力的关系，并将其反馈回OpenSees，实现与数值子结构的通信，并进行下一步的动力分析。如图5所示，本次试验使用OpenFresco中的梁柱试验单元(beam column test element)[19]，由于仅考虑单向加载，且试验子结构水平布置规整，试验单元节点处仅包含3个平面内的位移ub,1、ub,2、ub,3以及对应的反力q1、q2、q3。在1.3.1节中，我们将试验子结构空间框架看成一个整体，仅考虑边界处的纯平动自由度，而竖向荷载通过千斤顶来施加。因此，真正需要去控制的便是试验单元节点处的平动自由度ub,1和反力q1。

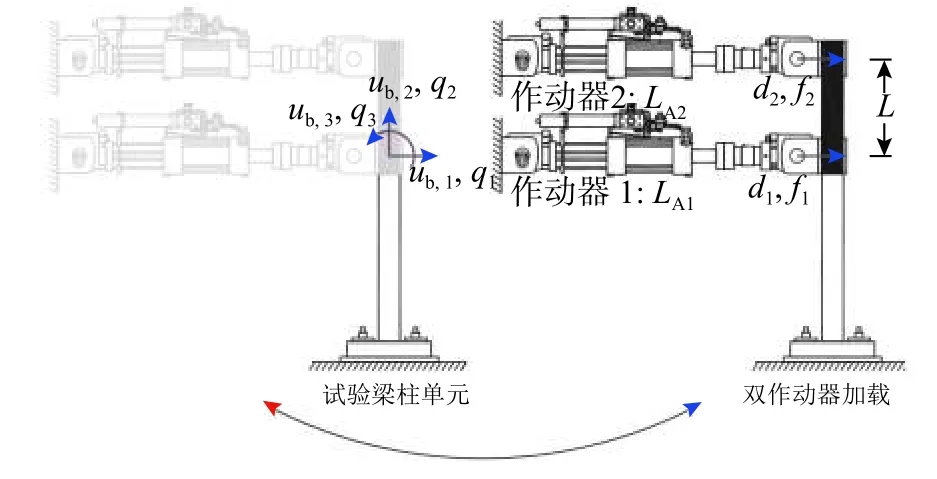
图5 梁柱试验单元与双作动器加载的数据通信[19]Fig.5 Data communication between beam-column test element and two-actuator experimental setup

在混合试验过程中，两个作动器保持等位移的同步加载，即d1=d2，测得的当前步试验子结构反力分别为f1和f2，则试验单元接收到的反馈信号为ub,1=d1=d2，q1=f1+f2。从而实现试验单元与试验子结构加载的等效通信。

1.3.3测量方案

如图6所示，试验子结构的整体侧向位移值、柱脚位移值、消能梁段的转角位移值以及加载段的侧向位移值均通过线位移传感器测量。试验子结构的应变采用电阻应变计测量，应变片布置于柱脚翼缘、支撑翼缘、框架梁翼缘及消能梁段翼缘处，应变花布置于柱脚节点腹板和消能梁段腹板处。

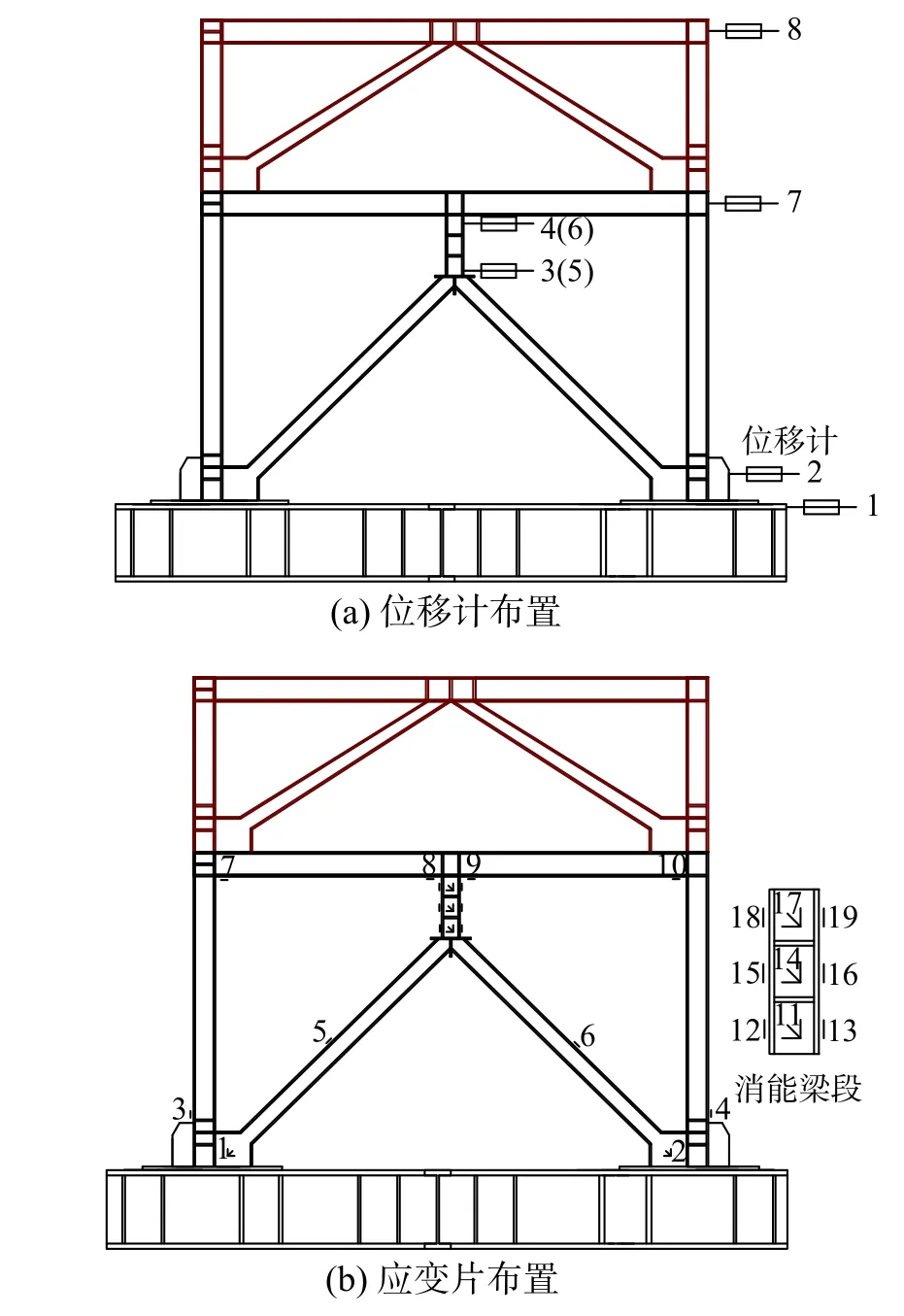
图6 测点布置Fig.6 Instrumentation arrangement of experimental substructure

1.4 荷载工况

原型结构位于抗震设防烈度8 度(0.2g)区，设计地震分组为第二组，Ⅱ类场地。根据《建筑抗震设计规范》[4]，选取El Centro波、Taft 波和兰州波作为原始输入地震波。将3种地震波的加速度反应谱和平均值与标准谱进行比较，如图7所示。具体的加载制度如表5所示。加速度相似比为1.2∶1。在试验开始和每个加载阶段结束后，通过小位移加载获得试验子结构的刚度。结构阻尼采用瑞利阻尼，多遇地震阻尼比为0.045，罕遇地震阻尼比为0.05。

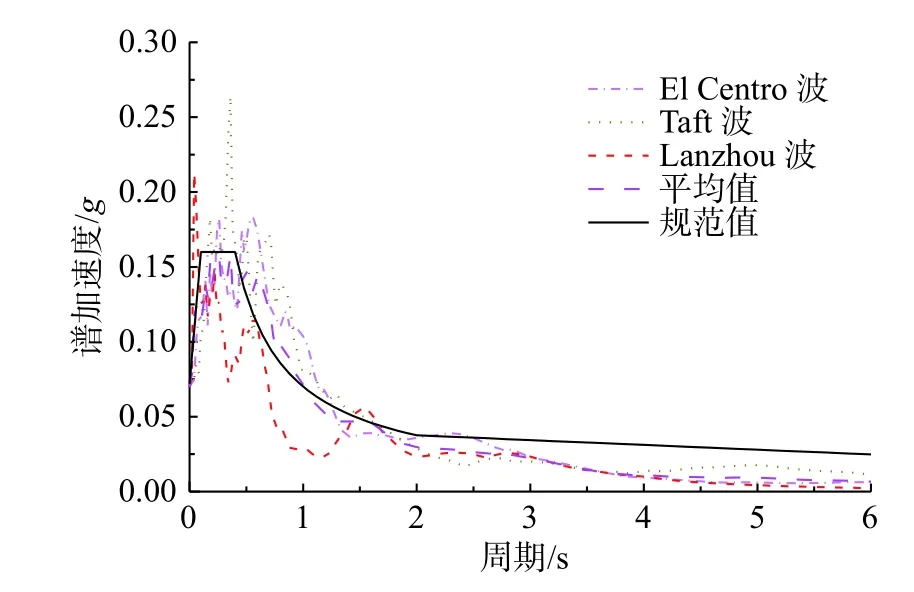
图7 加速度反应谱Fig.7 Acceleration response spectra

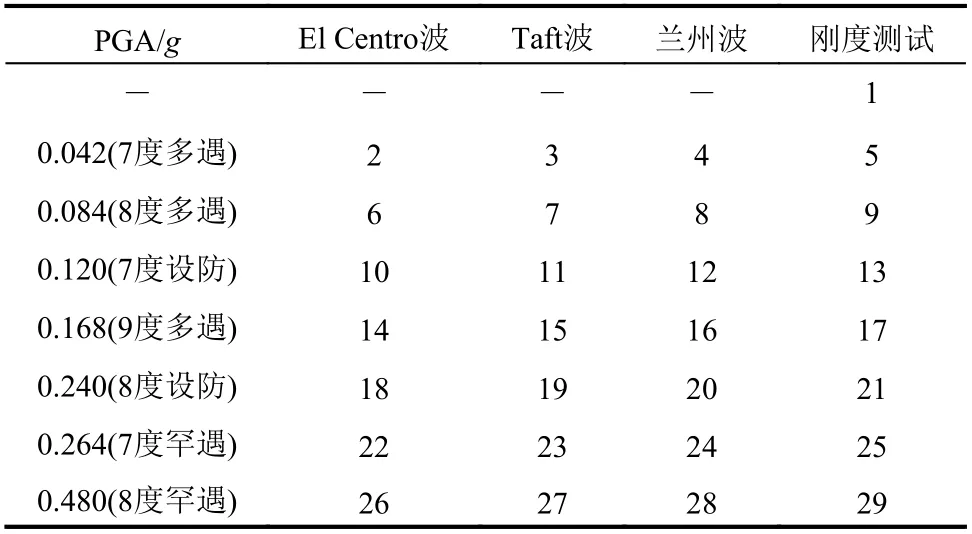
表5 荷载工况序列Table 5 Sequence of hybrid tests

2 混合试验现象

在整个试验过程中，试验子结构并未出现倒塌、失稳等破坏现象，变形主要产生在消能梁段截面处。当PGA 小于0.240g时，由于试件地震响应较小，并未观察到明显现象。当PGA 达到0.240g时，模型第一次出现响声，观察到消能梁段的腹板与翼缘连接处焊缝以及翼缘与框架梁连接处焊缝均出现了掉皮现象(见图8(a)、图8(b))。当PGA 达到0.480g时，消能梁段处焊缝掉皮现象更加明显，消能梁段与支撑连接一侧的腹板区格出现了轻微的应力屈服迹线，而与框架梁连接一侧的翼缘位置也出现了微小的裂缝(见图8(c)、图8(d))。表明在地震波作用下，使用低屈服钢材的消能梁段先发生塑性变形耗散能量，而框架梁柱由于使用高强度钢材仍然保持在弹性范围，符合结构抗震多道设防的理念。

图8 混合试验现象Fig.8 Hybrid test phenomena

3 试验结果分析

3.1 试验结果有效性验证

为了验证混合试验结果的有效性，利用OpenSees建立了全结构的纯数值模型来与试验结果进行比较。如图9所示，以PGA=0.084g的El Centro波作用下，模型一层的位移响应和基底剪力响应时程曲线为例。可以看出，在地震波作用下，混合试验模型的地震响应与纯数值模型分析结果基本吻合，在峰值处稍有误差。

图9 混合试验模型与纯数值模型比较Fig.9 Comparison of structural responses between hybrid test and pure numerical models

3.2 模型整体响应

3.2.1位移响应

图10给出了混合试验模型每一层相对于基础的最大水平位移。可见看出，模型结构在3 种地震波作用下的位移响应均呈倒三角形分布。El Centro波的位移响应最大，兰州波的位移响应最小。在多遇地震作用下，模型各层的相对侧向位移不明显，说明结构整体位移响应较小。当PGA达到0.480g时，各楼层的最大相对位移发生显著变化，且底层增幅最大，说明在罕遇作用下，模型侧移主要集中在底层，这也是本次混合试验选取模型底层作为试验子结构的原因。

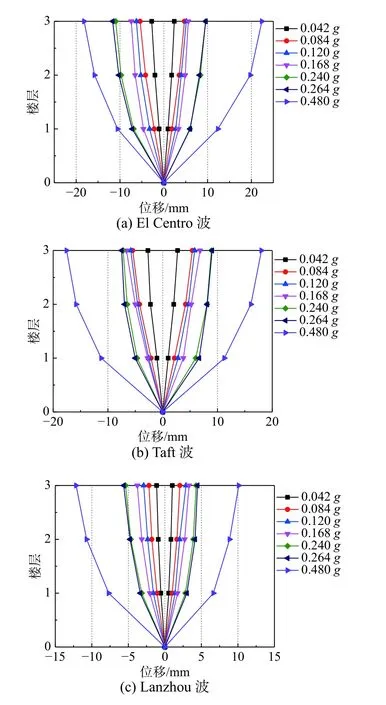
图10 最大位移响应Fig.10 Maximum displacement responses

表6列出了不同加载工况下混合试验模型的最大层间侧移。可以看出，模型最大层间侧移出现在一层。在多遇地震作用下，模型结构的最大层间位移为1/414，满足抗震规范的要求，即多层和高层钢结构的弹性层间位移小于1/250。在罕遇地震作用下，模型结构的最大层间位移为1/145，小于抗震规范对多层和高层钢结构弹塑性层间位移的限值1/50。

表6 最大层间侧移Table 6 Maximum inter-story driftsof hybrid test model

3.2.2加速度放大系数

模型的加速度放大系数(各楼层的峰值加速度与PGA 的比值)如图11所示。可以看出，混合试验模型的加速度放大系数在顶层最大，基本呈倒三角形分布。随着地震波加速度峰值的增大，各楼层的加速度放大系数有明显减小的趋势，说明结构损伤随地震强度的增大而增大，刚度随地震强度的增大而减小。

3.2.3消能梁段转角

图12给出不同加载阶段各层的最大消能梁段转角与相应层的最大层间侧移之间的关系，其中消能梁段转角值根据式(2)求得。可以看出，当PGA 小于0.168g时，最大消能梁段转角和层间侧移近似呈线性变化，表明模型基本处于弹性状态。当PGA 达到0.480g时，由于消能梁段的塑性变形，模型的刚度降低，折线斜率有增大的趋势。模型一层的层间侧移最大，因此相应层梁段的转动也最大。消能梁段的最大转角出现在PGA 为0.480g的El Centro波作用后，为0.0337 rad，小于美国钢结构建筑抗震规范AISC341-16(2016)[20]规定的剪切型消能梁段的转角限值，γp≤0.08 rad。

式中：γ 为消能梁段转角值；l3和l4分别为消能梁段处位移计3和4所测得的位移值；Llink为消能梁段长度，此处取值为350 mm。

3.3 试验子结构

3.3.1刚度退化

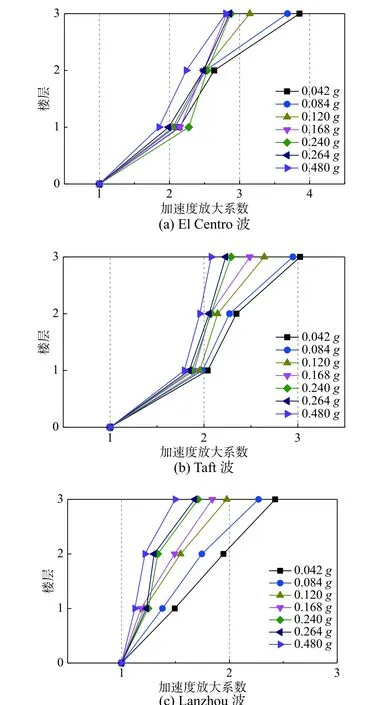
图11 加速度放大系数Fig.11 Acceleration amplification factors

图12 消能梁段转角Fig.12 Graph of link rotation v.s.inter-story drift

在混合试验过程中，作动器测量了试验子结构在各级加载工况后的侧向刚度值。如图13所示，在多遇地震作用下，试验子结构刚度与初始刚度相比变化不大，说明结构仍处于弹性状态，与试验现象一致。当PGA 达到0.480g时，消能梁段处焊缝轻微开裂，模型刚度显著降低，最大刚度退化率达到了-13.846%。

3.3.2滞回曲线

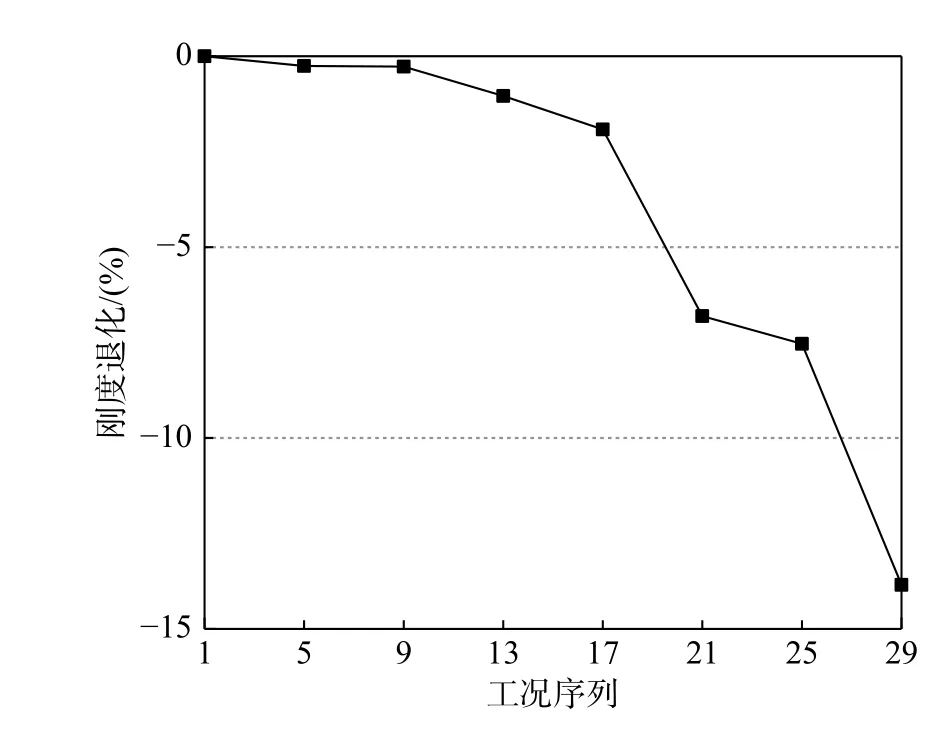
图13 刚度退化Fig.13 Stiffnessdegradation of experimental substructure

图14给出了试验子结构在不同强度El Centro波作用下的基底剪力-顶点位移滞回曲线，其中基底剪力由2个水平作动器的反馈力之和获得。从图中可以看出，当PGA 达到0.084g时，滞回曲线基本为一条直线，表明试验子结构处于弹性状态。当PGA 达到0.240g时，基底剪力与水平位移之间已经有形成滞回环的趋势，表明试验子结构已经由弹性状态向弹塑性状态转变。当PGA 达到0.480g时，消能梁段翼缘与框架梁连接之间的焊缝产生裂缝，试验子结构的非线性特征更加明显，形成了明显的滞回环。

3.3.3累积能量耗散

耗能是反映结构抗震性能的重要指标之一。如图15所示，根据试验子结构的基底剪力和顶点位移滞回曲线，得到了试验子结构在不同El Centro波作用下的累积耗能时程响应。可以看出，当PGA 达到0.084g时，模型的总累积耗能较小，第15 s时的累积耗能为0.26 kJ，表明试验子结构基本处于弹性状态，滞回耗能主要来自弹性应变能，总的累积能量耗散时程响应呈波浪式增长。当PGA 达到0.480g时，结构耗能响应的波动值出现了较大的飞跃，第15 s时的累积耗能为8.92 kJ。消能梁段的塑性变形和焊缝裂缝的增多使结构的塑性损伤不断累积，表明模型从弹性状态向弹塑性状态转变。

3.3.4测点应变

图16显示了在El Centro波作用下试验子结构的测量应变响应。图中的纵坐标相对应变ε/εy为测点实测应变与对应钢材的屈服应变之比。可见，消能梁段腹板的应变值(测点11、测点14、测点17)明显高于翼缘位置的应变值(测点12、测点13、测点15、测点16、测点18、测点19)，说明消能梁段以腹板的剪切变形为主。同时可以观察到，消能梁段位置的所有测点应变(测点11～测点19)始终大于梁柱和支撑位置的应变(测点1～测点10)，这均与我们的结构设计思想相符。

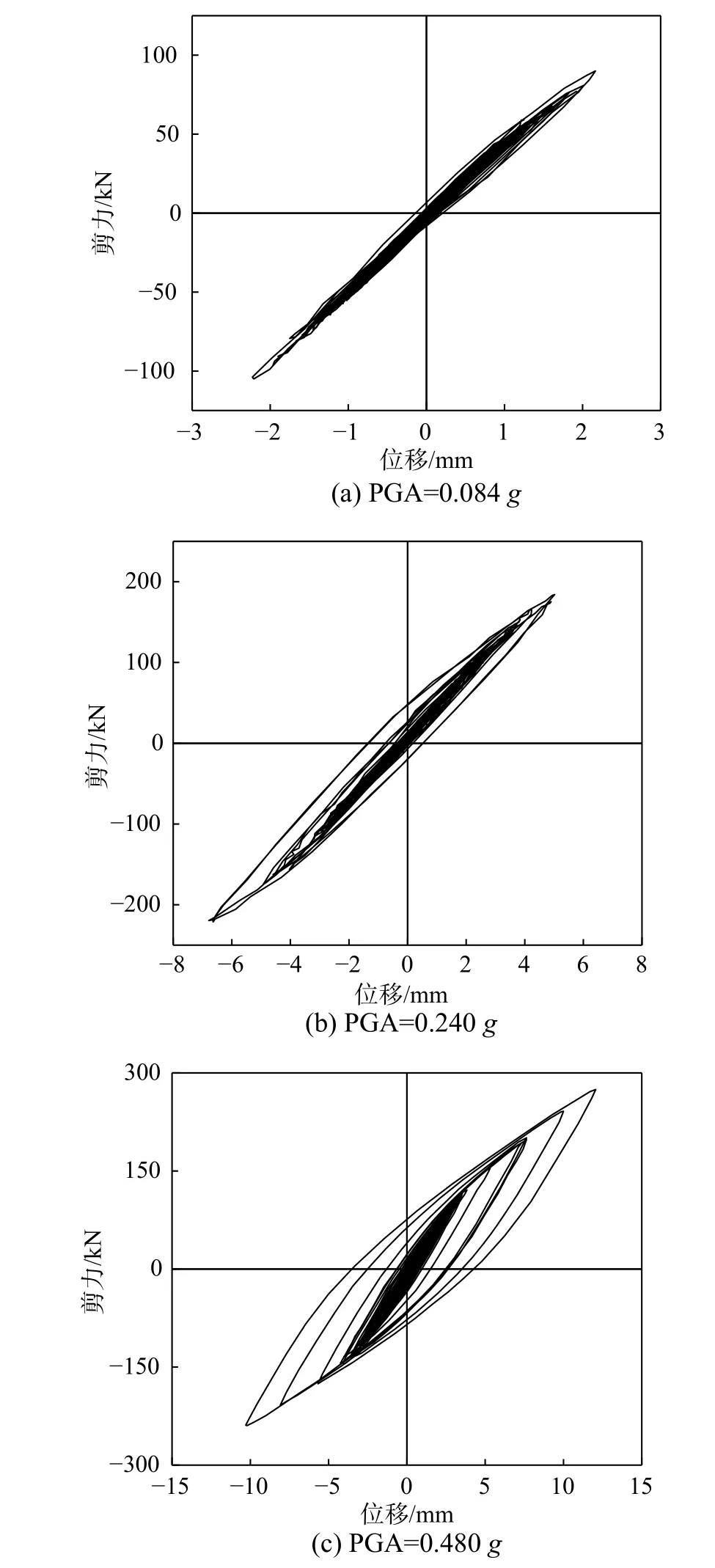
图14 滞回曲线Fig.14 Hysteretic loopsof shear v.s.displacement

随着加速度峰值的增大，各测点的应变值稳步增长，当PGA 达到0.084g时，试验子结构结构 处 于 弹 性 状 态(ε/εy＜1)。当PGA 达到0.240g时，消能梁段腹板的应变值(测点11、测点14、测点17)接近屈服应变，说明结构有进入塑性的趋势。当PGA 达到0.480g时，消能梁段腹板测点的应变值显著增加，超过了屈服应变，且靠近框架梁一侧增幅最大。在高强钢组合Y形偏心支撑框架体系中，由于框架梁柱采用高强钢，消能梁段采用普通钢，在地震波作用下，消能梁段首先发生塑性变形并耗散能量，而框架梁柱仍能保持弹性，从而实现多方面抗震设防的目的。

图15 累积能量耗散Fig.15 Cumulative energy dissipation time-history responses

图16 试验子结构测点应变Fig.16 Variation of strain of experimental substructure

4 结论

本文通过对一个3层3跨的高强钢组合Y 形偏心支撑框架进行子结构混合试验，主要得到以下结论：

(1)在混合试验模型的建立过程中，利用OpenSees建立了混合试验模型的数值子结构，使用OpenFresco提供的试验梁柱单元双作动器加载模式实现了空间框架试验子结构的边界加载和单元等效。与全结构纯数值模型的模拟结果比较可以看出，由OpenSees、OpenFresco和MTS加载设备组成的混合试验系统能够有效地对空间框架子结构模型进行地震响应模拟。

(2)在多遇地震(PGA=0.168g)和罕遇地震(PGA=0.480g)作用下，混合试验模型的最大层间侧移分别为1/414和1/145，符合抗震设计规范对多高层钢框架结构层间侧移的限值。当PGA 小于0.480g时，试验子结构的基底剪力和顶点侧移基本呈线性变化。当PGA 达到0.480g时，由于消能梁段的塑性变形，模型的刚度降低明显。消能梁段的最大转角为0.0337 rad，小于美国钢结构建筑抗震规范AISC31-16规定的极限值。

(3)试验子结构的应变分析表明，消能梁段以剪切变形为主。当PGA 达到0.480g时，消能梁段腹板的应变值超过屈服应变，说明结构已进入塑性阶段，开始耗散地震能量，而框架梁柱仍能保持弹性，实现了结构多道抗震设防的目的。