胶结型含可燃冰砂土剪切特性的离散元模拟

王 璇，徐 明

(清华大学土木工程系，北京100084)

可燃冰的主要成分为甲烷水合物，是由甲烷分子和水分子在高压、低温条件下生成的亚稳态固体物质，广泛分布于深海和常年冻土区域[1]。作为一种燃烧热高、污染少的新型绿色能源，可燃冰在近些年来得到了人们的广泛关注。目前，许多国家已经制定了可燃冰资源开发规划，并开始大力发展可燃冰开采技术[2]。

然而，在深海开采可燃冰过程中极易引发海底坍塌、滑坡，进而诱发地震、海啸等地质灾难[3]，造成巨大的人员伤亡和财产损失。为了进一步完善可燃冰开采技术，避免可燃冰开采过程中灾害的发生，对含可燃冰土体力学特性的深入研究具有非常重要的意义。

可燃冰在砂土颗粒间的分布主要有填充、胶结、包裹、骨架等4种形态[4]，不同的分布形态会使含可燃冰砂土表现出不同的力学性质。对此，学者们已经进行了有限的试验研究。其中，Masui等[5]分别向含冰砂和含水砂中通入甲烷气体，诱导生成填充型和胶结型含可燃冰砂土，并对其实施三轴试验，探究了可燃冰形态差异对于砂土抗剪强度和刚度的影响；Li等[6]通过三轴试验探究了可燃冰饱和度和围压对于填充型含可燃冰砂土内摩擦角与粘聚力的影响；Miyazaki 等[7]通过三轴试验探究了可燃冰饱和度、围压、温度等对于胶结型含可燃冰砂土抗剪强度的影响；Pinkert 等[8]对于剪切过程中胶结型含可燃冰砂土的胶结破坏形式进行了探究。此外，可燃冰仅能在高压、低温条件下保持稳定，在开采过程中极易发生分解生成甲烷气体，因此Hyodo等[9]、Song 等[10]、Zhang等[11]通过试验研究了可燃冰分解对于含可燃冰土体力学性质的影响。上述试验初步揭示了含可燃冰砂土的宏观力学性质，但对于加载过程中土体的微观变化难以进行有效的观测，此外，真实试验受到取样制样难、试验成本高等制约。

离散元法是一种用于反映颗粒材料力学性质和颗粒间相互作用的数值模拟方法，于1979 年由Cundall 等[12]提出，目前在结构、岩土、机械等多个领域得到了广泛的应用[13-15]。近年来，对含可燃冰砂土的离散元模拟已经成为一种新的研究思路。Brugada 等[16]通过在砂土颗粒间生成直径更小的可燃冰颗粒，建立填充型含可燃冰砂土的离散元模型，探究了填充型可燃冰对于砂土力学性质的影响；蒋明镜等[17-19]通过分析前人试验结果并类比水泥、环氧树脂等其他胶结材料，提出了一种含可燃冰砂土微观力学胶结模型的建立方法，并在此基础上使用PFC2D软件，采用在所有颗粒接触处添加平行粘结的方式对胶结型含可燃冰砂土进行了离散元模拟；Xu 等[20-21]利用离散元方法模拟了含可燃冰解离气体砂土的不排水剪切试验。然而，目前已有的成果主要集中在反映含可燃冰砂土的宏观力学性质上，而对于一些宏观现象仍缺乏相应的细微观阐释。此外，目前已有模型往往通过改变粘结强度[17-19]反映可燃冰含量的变化，然而二者之间的联系较为抽象，函数关系难以确定。

本文在前人研究的基础上，提出一种新的胶结型含可燃冰砂土离散元模拟方法，通过在颗粒间添加接触粘结模拟胶结型可燃冰的存在。该方法通过改变添加粘结的数量反映可燃冰含量的变化，使得模型与真实土体之间的对应关系更为直观。随后，本文利用PFC2D软件对上述模型进行了排水剪切试验模拟，通过与Masui等[5]试验对比验证了模型的合理性。在此基础上，本文探讨了宏观力学特性和细观现象之间的对应机理及关联，通过分析粘结断裂、剪切带内外土颗粒运动等细观现象，对偏应力变化、体胀等宏观特性进行了进一步阐释。

1 离散元模拟

1.1 可燃冰胶结模型选取

本文利用PFC2D软件建立可燃冰胶结模型，该模型包括砂土颗粒模型和可燃冰模型两部分。

其中，砂土颗粒选用线性接触模型，法向刚度和切向刚度均为常数。模型不考虑砂土颗粒形状对于土体性质的影响，所有砂土颗粒均采用单个具有单位厚度的圆盘单元来模拟。模型尺寸取为160 mm×80 mm。

对于砂土颗粒间以胶结形态存在的可燃冰，选取PFC2D软件中内置的粘结模型进行模拟。PFC2D中常用的粘结模型包括平行粘结和接触粘结[22]，通过将分别添加上述两种粘结模拟所得的双轴试验曲线与前人真实试验曲线对比，确定最终选用的粘结模型为接触粘结。

可燃冰饱和度SMH指土体中可燃冰体积占土体总孔隙的百分比，它是影响含可燃冰砂土力学性质的一项重要指标。在本胶结模型中，利用颗粒粘结率Rb来反映真实土体中可燃冰饱和度SMH的变化。颗粒粘结率Rb定义如式(1)所示：

式中：Nt表示PFC模型的圆盘单元间接触总数量；Nb表示添加接触粘结的数量。模型中每个接触粘结的添加位置随机，以此模拟天然条件下可燃冰生成位置随机的特点[23]。由于真实土体中可燃冰含量的多少与模型中添加粘结的数量直接相关，因此令模型颗粒粘结率Rb的取值与真实土体中可燃冰饱和度Rb的大小相同，以便直观反映二者之间的对应关系。

1.2 离散元模型建立

为了便于同已有试验数据进行比较，本模型在建模和参数确定过程中均选用Masui等[5]所进行的人工合成胶结型含可燃冰砂土三轴排水试验作为参照。在Masui 试验中，选取初始水饱和度为30%～70%的Toyoura 砂制作样品，对该含水砂土样品施加指定温度和围压，随后通入甲烷气体诱导生成甲烷水合物，诱导完成后在保持围压不变的情况下对试样实施三轴剪切[5]。

对于离散元模型，首先定义上下左右4个方向的墙单元，然后用膨胀法生成20 117个颗粒直径在0.6 mm～1.0 mm 随机分布的圆盘单元，由此得到初始试样。该模型取墙单元刚度与圆盘单元刚度相等，法向刚度为切向刚度的1.5倍。确定圆盘单元摩擦系数、圆盘单元刚度等取值时，选用Masui等[5]试验所得的纯砂应力-应变曲线进行参数标定，调整模型参数使离散元纯砂模型剪切强度、刚度等与真实试验吻合。最终确定墙单元与圆盘单元的详细参数如表1所示。

表1 离散元模型参数取值Table 1 Parameters of DEM model

为模拟Masui 等[5]试验中诱导含可燃冰砂土的生成步骤，在形成离散元初始试样后，利用伺服机制为试样施加指定围压，然后在颗粒间接触处添加接触粘结，用于模拟胶结型可燃冰的存在。

接触粘结的参数包括法向和切向强度，对于本模型中的粘结强度参数，选取Masui等[5]试验中SMH=55.1%的含可燃冰砂土应力-应变曲线进行标定，调整参数使Rb=55.1%时离散元模型抗剪强度与真实试验结果相同，确定模型切向与法向粘结强度均取1.1×104Pa。经过以上步骤所得的离散元模型示意图如图1。

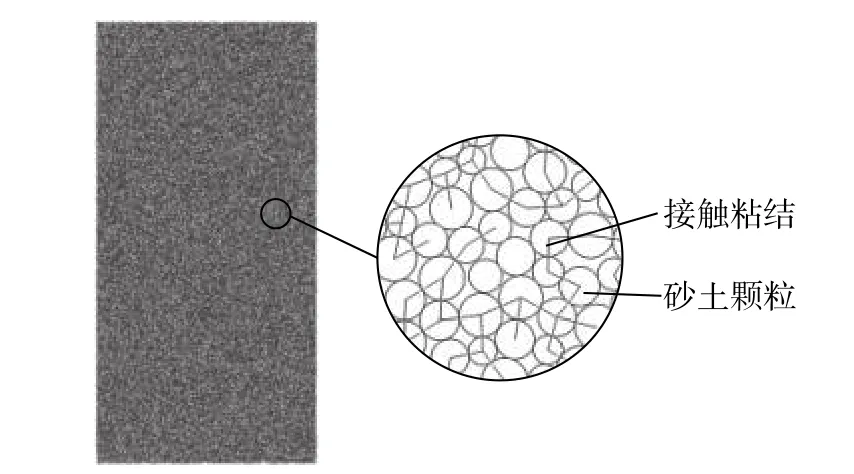
图1 胶结型含可燃冰砂土离散元模型Fig.1 DEM model of cemented hydrate-bearing sands

最后，在保持围压的情况下控制上下侧墙单元的位移，墙单元运动形成对土单元的压力，以此实施对已添加粘结试样的加载，模拟双轴剪切试验过程。离散元模型中不直接模拟水的存在，施加围压和剪切的过程直接作用在土单元骨架上，总应力等于有效应力，从而模拟排水条件。通过实时记录各墙单元的位移值，可计算出加载过程中试样的轴应变和体应变变化；通过实时记录各墙单元所受法向应力，可计算出加载过程中试样的应力变化。

通过改变颗粒粘结率Rb、围压等参数，探究不同条件下胶结型含可燃冰砂土的宏观与细观特性。

2 模拟结果及分析

2.1 宏观力学性质

首先探究模型颗粒粘结率Rb变化对于砂土抗剪强度与体应变的影响。对前文所述的离散元模型施加围压σ3=1 MPa，模拟得不同颗粒粘结率Rb(0%、25.7%、40.7%和55.1%)条件下的胶结型含可燃冰砂土应力-应变曲线如图2所示，体应变曲线如图3所示。图中同时给出了同等试验条件下Masui 等[5]三轴试验的结果对比。

可以看出，通过改变模型颗粒粘结率Rb可以较好地定性反映不同可燃冰饱和度SMH条件下含可燃冰砂土排水剪切力学特性的变化，且具体表现为：

图2 不同颗粒粘结率R b/可燃冰饱和度S MH 下应力-应变关系Fig.2 Stress-strain curveswith different bonding ratios R b/hydrate saturation S MH

图3 不同颗粒粘结率R b/可燃冰饱和度S MH 下体应变关系Fig.3 Volumetric curves with different bonding ratios R b/hydrate saturation S MH

1) 胶结型含可燃冰砂土峰值强度与刚度随SMH/Rb的增大而增大，并在峰值强度后表现出更强烈的应变软化现象；

2)试样加载过程中先发生体缩后发生体胀，SMH/Rb越高，试样的剪胀性越大。

从定量上看，该模型模拟出的土体峰值强度大小与真实试验结果较为吻合，而体应变偏小，造成差异的原因可能包括未考虑砂土颗粒形状影响、模型仅限于二维模拟等。

进一步地，探究排水剪切过程中胶结型含可燃冰砂土内摩擦角φ与粘聚力c值的变化规律。参照Masui 等[5]试验，取离散元模型颗粒粘结率Rb分别为0%、25.4%和34.25%，并对每个Rb取值下的模型分别施加1 MPa、2 MPa、3 MPa 及5 MPa围压进行排水双轴试验模拟，绘制摩尔圆获得破坏包络线，计算得内摩擦角φ与粘聚力c值，试验与模拟结果对比如图4所示。

图4 不同颗粒粘结率R b/可燃冰饱和度S MH下内摩擦角φ及粘聚力c 变化Fig.4 Friction angle φ and cohesion c with different bonding ratios R b/hydrate saturation S MH

对比可知，本文提出的离散元模型模拟结果与Masui 试验[5]结果较为吻合，二者均反映出以下规律：胶结型含可燃冰砂土在排水剪切过程中，随着SMH/Rb的增加，内摩擦角φ大小变化不大，而粘聚力c的值呈显著的增加趋势。由此说明和纯砂相比，胶结型可燃冰主要通过提高砂土的粘聚力进而提高抗剪强度，而其对于内摩擦角的影响较小。

考虑上述现象中可燃冰的存在带来的影响，可以作出如下解释：由于可燃冰主要作为胶结物质存在于砂土颗粒之间，因此仅能提供颗粒与颗粒之间的粘聚作用，可燃冰饱和度越大，颗粒接触处存在胶结物质的比例越高，因此粘聚力c值越高，且初始刚度越大；而可燃冰的存在对土颗粒本身的颗粒咬合、摩擦系数等影响不大，因此可燃冰饱和度变化对于内摩擦角φ的影响较小；此外，含可燃冰砂土在剪切过程中表现出比纯砂更大的剪胀性，其原因是胶结型可燃冰的存在能将多个砂土颗粒粘结成为较大的颗粒簇，在剪切错动中更容易形成较大的孔隙。

2.2 粘结断裂演化

研究表明，胶结型含可燃冰砂土在排水剪切过程中发生可燃冰的破碎或脱粘[8]，而在本离散元模型中对应为接触粘结的断裂。接触粘结的断裂标准为颗粒粘结处受到的切向应力大于切向粘结强度，或者法向应力大于法向粘结强度。为了定量描述加载过程中模型接触粘结断裂的数量变化规律，此处定义粘结断裂率Rbk如式(2)：式中，Nbr为发生剪切后断裂的接触粘结数量。

图5给出了围压σ3=1 MPa，模型颗粒粘结率Rb分别为0%、25.7%、40.7%和55.1%条件下的应力-应变曲线和粘结断裂率Rbk变化曲线对比(当Rb=0%时，模型不添加粘结，故不存在对应的粘结断裂率Rbk变化曲线)。

图5 不同颗粒粘结率R b 下粘结断裂率R bk-轴应变变化关系Fig.5 Relationship between bond breaking ratio R bk and axial strain with different bonding ratios R b

如图5所示，对于不同颗粒粘结率Rb的模型，均在加载至ε1=1%时才开始发生粘结断裂，且其后加载至相同轴应变条件下，Rb越高，土体的粘结断裂率Rbk越高。此外，由图5可以看出模型中粘结的断裂情况与偏应力的变化趋势密切相关。利用该结果可以解释胶结型含可燃冰砂土剪切破坏过程中宏观与细观特性之间的对应关系，其大致可以分为3个阶段：

1)当轴应变小于1%左右时，接触粘结几乎没有发生破坏，粘结断裂率Rbk约等于0，即土体中可燃冰胶结物完好，此时偏应力近似随轴应变的增加而线性增大，该阶段可近似看作弹性阶段，土体尚未发生破坏。

2)当轴应变到达1%～8%左右时，粘结断裂率Rbk进入明显的快速增长阶段，即可燃冰的胶结作用受到大量破坏，此时偏应力先达到峰值并随后开始下降，土体表现出应变软化的特性。当偏应力达到峰值时，Rbk曲线的斜率近似达到最大值。在这一阶段，土体发生剪切破坏。

3)当轴应变达到约8%时，粘结断裂率Rbk开始进入缓慢上升阶段，其增长速度不断下降并最终趋向于0；与此对应，偏应力曲线在这一阶段下降缓慢，至加载结束时，偏应力几乎不再变化。

图6给出了给定颗粒粘结率Rb=55.1%，分别施加围压σ3=1 MPa、σ3=2 MPa 和σ3=3 MPa 时应力-应变曲线和粘结断裂率Rbk变化曲线的对比情况。可以看出，不同围压条件下的模型破坏同样表现为前文所述的3个阶段，且施加围压越大，Rbk越高，即可燃冰胶结物的破坏数量越多。

图6 不同围压下粘结断裂率R bk-轴应变变化关系Fig.6 Relationship between bond breaking ratio R bk and axial strain under different confining pressures

2.3 剪切带内外变化规律

在确定粘结断裂数量的基础上，进一步研究粘结断裂的位置分布规律。以围压σ3=3 MPa，颗粒粘结率Rb=55.1%为例进行分析。图7给出了加载至轴应变ε1=0%、ε1=3.5%、ε1=7%、ε1=14%这4个时刻的模型粘结断裂分布情况，其中灰色短线表示尚未发生断裂的粘结，红色短线表示已经断裂的粘结。由该图可以看出，随着轴应变的增加，发生断裂的粘结数逐渐增多。通过分析不同轴应变时粘结断裂的分布情况，可以大致反映出加载过程中剪切带的形状和形成过程。对于该模型，剪切过程中形成多条呈“X”状交叉的剪切带，粘结的断裂主要发生在剪切带内部。由此可以推断，对于胶结型含可燃冰砂土，排水剪切过程中可燃冰胶结物的破坏并不是均匀分布的，其破坏主要分布于土体剪切带的内部。

由图6可知，围压σ3=3 MPa，颗粒粘结率Rb=55.1%，加载至ε1=14%时，砂土粘结断裂率Rbk仅为20%左右，而曲线增长趋势已非常缓慢。该时刻对应于图7(d)，剪切带内部的绝大部分粘结已发生破坏，其中少量未破坏的粘结可使相邻的几个圆盘单元形成一个较大的颗粒簇，而剪切带外部粘结在加载过程中破坏非常少。图6与图7对比可知，砂土粘结断裂率Rbk的增长主要取决于剪切带内部粘结的断裂情况，当剪切带内部粘结充分破坏时，粘结断裂率Rbk便几乎不再继续增加。

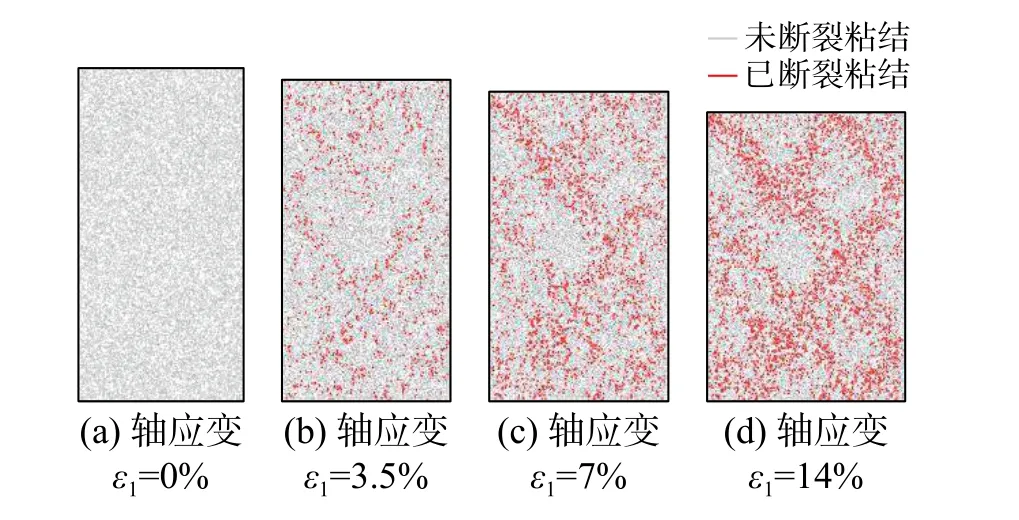
图7 不同轴应变下砂土粘结断裂分布(R b=55.1%)Fig.7 Bond breaking distribution at different axial strains(R b=55.1%)

图8给出了围压σ3=3 MPa，颗粒粘结率Rb=55.1%条件下，加载至轴应变ε1=0%、ε1=3.5%、ε1=7%、ε1=14%这4个时刻砂土颗粒的转动示意图。可以看出，在加载至轴应变大于7%后，剪切带内外颗粒的转角出现明显差异，其中剪切带内部的颗粒转角随轴应变的增加而显著增加，而外部颗粒的转角基本保持在30°以内，未发生明显变化。已有研究表明，纯砂土在剪切过程中颗粒运动存在类似规律，即剪切带内部颗粒转角明显大于剪切带外部[24-25]，结合纯砂运动规律，分析添加粘结后含可燃冰砂土剪切带内外颗粒转角存在差异的原因，可能是由于剪切带内部的粘结发生大量断裂，砂土颗粒失去约束，因此仍能发生自由转动；而剪切带外部的粘结发生断裂较少，砂土颗粒受到粘结的约束，因此颗粒转角较小。

图8 不同轴应变下砂土颗粒转角(R b=55.1%)Fig.8 Rotation of particlesat different axial strains(R b=55.1%)

为了探究离散元模型加载过程中局部孔隙率的变化情况，将模型划分为30×30个大小相等的网格，计算每个网格内砂土颗粒的孔隙率，作为整体模型中该网格位置的局部孔隙率。图9 给出了围压σ3=3 MPa，颗粒粘结率Rb=55.1%条件下，加载至轴应变ε1=0%、ε1=3.5%、ε1=7%、ε1=14%时模型的局部孔隙率变化情况。由图9可以看出，随着轴应变的增加，剪切带外部的孔隙率变化不明显，而剪切带内部的孔隙率有显著增加。造成这一现象的原因可能是在加载过程中，剪切带外部的砂土颗粒受粘结约束较多，呈同一方向的定向运动，因此仍能保持原先的紧密堆积；而剪切带内部的砂土颗粒由于粘结断裂而受约束减少，部分颗粒形成粒径较大的颗粒簇，且剪切过程中颗粒发生相互错动，因此可以形成较大的孔隙，如图10所示，图中箭头表示砂土颗粒位移矢量。

图9 不同轴应变下砂土局部孔隙率(R b=55.1%)Fig.9 Local porosity of sand at different axial strains(R b=55.1%)

图10 剪切带内外颗粒位移对比(ε1=14%)Fig.10 Particle displacement inside and outside shear band (ε1=14%)

在模型划分网格的基础上，在剪切带内外分别取多个大小为3×3网格的测量单元，计算每个测量单元的孔隙率，并分别求出剪切带内部和外部测量单元孔隙率的平均值，用以探究不同颗粒粘结率Rb条件下模型剪切带内外孔隙率变化情况。取围压σ3=3 MPa，颗粒粘结率分别为Rb=0%、Rb=25.7%、Rb=40.7%和Rb=55.1%，加载至轴应变ε1=14%进行分析，结果如图11所示。由图11可知，对于纯砂土(Rb=0%)和含可燃冰砂土来说，加载至该轴应变条件下，剪切带内部孔隙率均明显高于剪切带外部；同时可以看出，加载至该轴应变时，模型颗粒粘结率Rb越高，剪切带内部孔隙率越大，而剪切带外部孔隙率变化不大。这一现象可以较好地印证前文“可燃冰饱和度SMH越高，试样的剪胀性越大”的试验结论，并进一步说明剪切带内部的孔隙率变化是造成试样体胀的主要因素。

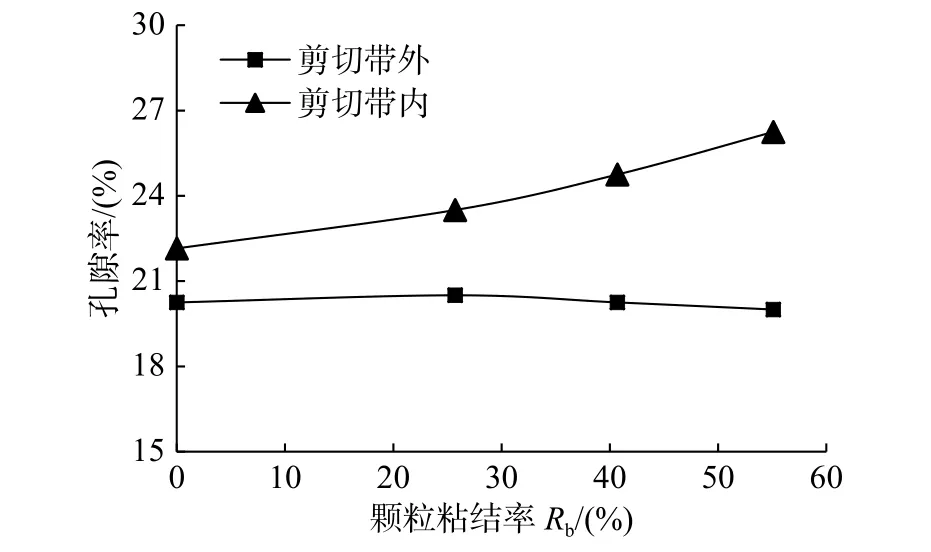
图11 ε1=14%时不同颗粒粘结率R b砂土剪切带内外孔隙率Fig.11 Porosity of sands inside and outside shear band with different bonding ratios R b at ε1=14%

3 结论

本文通过引入颗粒粘结率Rb这一指标来反映可燃冰饱和度SMH变化带来的影响，利用砂土颗粒间添加接触粘结的方式建立了胶结型含可燃冰砂土的离散元模型，并对该模型进行了排水双轴剪切试验的模拟。通过与Masui 等[5]真实试验结果的对比，本文验证了离散元模型的可靠性，并在此基础上对于模拟结果进行了宏观和细观两个层次的分析。分析结果表明：

(1)含胶结型可燃冰砂土的抗剪强度、刚度、应变软化程度、以及剪胀性均随可燃冰饱和度SMH的增大而显著增大；

(2)可燃冰的存在对于砂土抗剪强度的影响主要体现在对粘聚力c的影响上，可燃冰饱和度SMH的增大可导致粘聚力c的增加，但内摩擦角φ的大小几乎不随SMH改变而改变；

(3)加载过程中，模型粘结断裂率Rbk随轴应变的增大而增大，其变化过程大致可以分为3个阶段，且与宏观上偏应力的变化相互对应，密切相关；

(4)在剪切过程中，胶结型含可燃冰砂土在剪切带内外的变化具有明显差异。其中剪切带内部胶结物发生大量破坏，砂土颗粒转动和局部孔隙率明显增加；剪切带外部的胶结物发生破坏较少，砂土颗粒几乎不发生转动。

(5)剪切带内部的孔隙率变化是造成试样体胀的主要因素，加载至相同轴应变时，可燃冰饱和度SMH越高，剪切带内部孔隙率越大。