平行磁化NdFeB钢丝绳无损检测仪开发

路正雄，郭 卫，张传伟，赵栓峰，王 渊

(西安科技大学 机械工程学院，陕西 西安 710054)

0 引 言

钢丝绳由若干钢丝捻制而成，具有高抗拉强度等特点[1]，在矿井提升[2]、斜拉桥[3]、海上油气工业[4]、起重机吊装[5]和电梯提升[6]等行业广泛应用，并且不同应用领域，钢丝绳的规格和特性也不同。钢丝绳在服役过程中，常常处于动载荷或过载荷的状态，并随时间的推移不断磨损或者腐蚀而不断劣化，最终导致钢丝绳产生局部的金属缺失甚至断丝[7]。这些缺陷将导致钢丝绳的机械强度、载荷分担能力以及使用寿命逐渐丧失。然而，各应用领域对钢丝绳使用的安全性要求很高[8]。因此，需要定期有效地检查钢丝绳的健康状况，以避免灾难性事故发生。

现有的钢丝绳无损监测方法有漏磁(MFL)检测方法[9]、声发射检测方法[10]、涡流检测法[11]、X-射线弹测法[12]等。在上述检测方法中，MFL检测方法是目前最为有效的钢丝绳无损检测方法。该方法利用永磁体将钢丝绳磁化使其达到磁饱和状态，此时由于钢丝绳的损伤缺陷使磁通泄露到周围的环境中去，即漏磁。这种漏磁现象被霍尔传感器[13]感应线圈[14]、磁通量闸门传感器[15]等一些磁传感器检测到。

传统的基于MFL法的钢丝绳测试仪由2个完整的圆环形永磁体组成，每个环形永磁体由4个半环磁铁组成，并分别安装在空心铁磁圆柱体轭的两端，然后使用非金属衬套将被检测的钢丝绳密封起来，以此来保护磁铁和检测电路。现有的钢丝绳检测仪均采用4个径向磁化半环磁铁[16]。所有的径向磁化环形磁铁只在固定的几个国家制造，这对径向磁化环形磁铁的使用带来极大的不便，而且增加了检测仪的成本。径向磁化环形磁铁很难实现理想的径向磁化，因为它需要2 500 kA/m量级的高磁化场，峰值磁化电流大约为30 kA[17]。然而，与径向磁化相比平行磁化磁体容易实现而且价格很低，因此，平行磁化磁体比径向磁化磁体更具有利用优势。

针对目前钢丝绳检测仪采用的径向磁化半环磁铁磁化难度高造成的检测仪成本高以及钢丝绳缺陷检测的灵敏度低等问题。采用平行磁化(NdFeB)永磁体代替径向磁化半环磁体，基于MFL原理提出一种利用平行磁化永磁体段构建钢丝绳测试仪的新方法，设计了漏磁信号检测系统，采用BP神经网络对平行磁化NdFeB永磁体构建的钢丝绳无损检测仪的断丝检测精度进行提升。该方法有效地解决了径向磁化技术的不足，降低了技术难度和生产成本，提升了钢丝绳缺陷的监测精度。

1 新型钢丝绳无损检测仪原理

Foster模型是漏磁检测的理论模型[18]，气隙中的磁场强度Hg为均匀分布，磁场强度与到气隙的距离成反比。漏磁通H可以分别表示为

(1)

(2)

式中Hg为磁场强度，T；Hy为气隙在轴向的漏磁通量，Wb；Hx为气隙在径向的漏磁通量，Wb；Lg为气隙的面积,mm2。如果x=0，漏磁通的值为

(3)

由式(3)可知，漏磁通的值与y成反比，与Hg和Lg的乘积成正比。因此，如果保持Hg恒定，漏磁通的值会随着气隙的增大而增大。

由式(3)可知，以下的等式可表示为

(4)

在这种情况下，漏磁通传感器的灵敏度与y2成反比。基于上述漏磁(MFL)原理设计基于平行磁化NdFeB磁体的钢丝绳缺陷检测仪结构，原理如图1所示，其中LF代表钢丝绳局部断丝区域，LMA代表钢丝绳局部材料缺失区域。该钢丝绳无损检测仪由2个安装在铁磁轭中的永磁体环组成，当磁化的钢丝绳插入测试仪时，检测仪会形成包括磁铁、钢丝绳、铁磁轭以及磁铁与钢丝绳间隙的磁回路。被永磁体磁化到饱和状态的钢丝绳，会在缺陷位置处发生磁通量泄漏，泄漏的磁通量可以由霍尔传感器等检测到，进而实现钢丝绳缺陷的诊断。

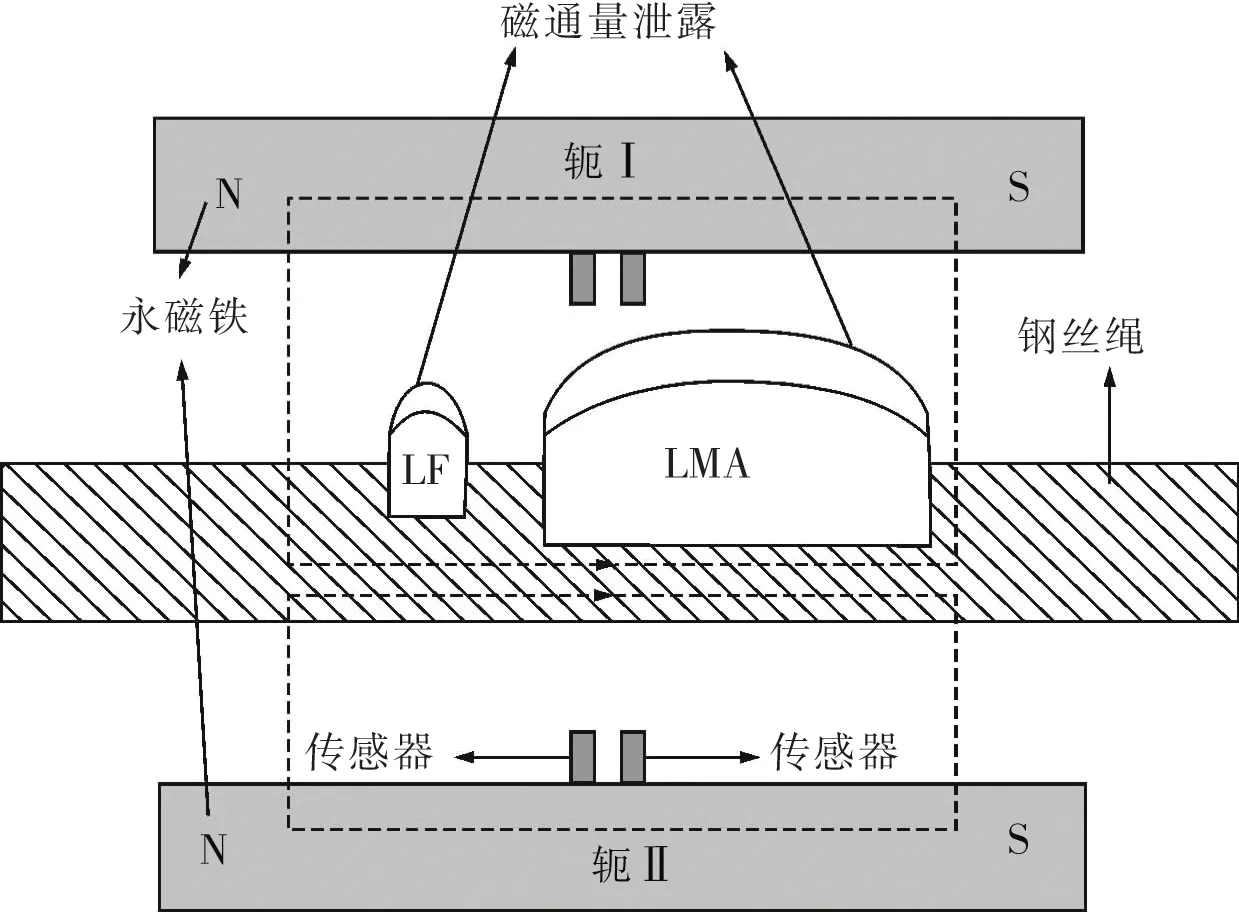
图1 基于MFL的钢丝绳测试仪原理Fig.1 MFL-based wire rope tester

2 平行磁化NdFeB钢丝绳无损检测仪设计与实现

2.1 平行磁化NdFeB磁体装配

平行磁化NdFeB磁体钢丝绳测试仪采用稀土永磁体。首先，用电火花线切割机将未磁化的环形NdFeB磁体切割成16个等弧段；然后，使用磁化器对NdFeB的每个弧段进行平行磁化，其中NdFeB磁体的平行磁化是指使磁体的外表面具有统一极性，内表面具有相反极性，如图2所示。

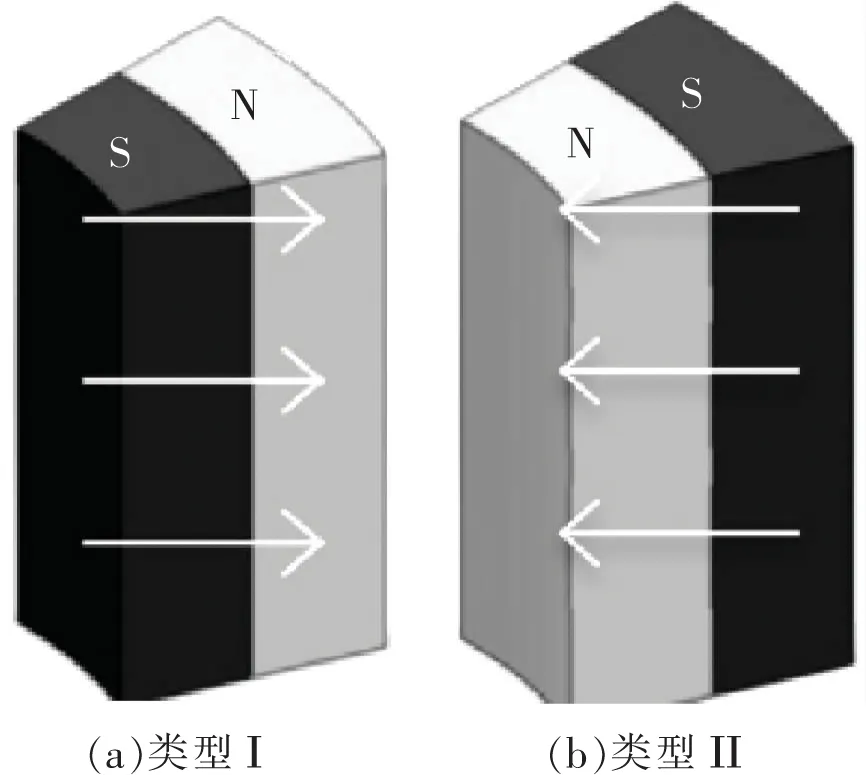
图2 平行磁化NdFeB磁体段Fig.2 Parallely magnetized NdFeB magnet segments

平行磁化NdFeB磁体段有2种类型：类型Ⅰ为北极位于外表面，南极位于内表面(如图2(a)所示)；类型Ⅱ为南极位于外表面，北极位于内表面(如图2(b)所示)。最后，将这些平行磁化的磁铁段组装成如图3所示的圆形环永磁体。在这32个磁铁段中，16个磁铁属于Ⅰ型，其余16个为Ⅱ型。将16块Ⅰ型磁铁段组装成圆环形磁铁1，如图3(a)所示，其他16个Ⅱ型磁铁组装成圆环形磁铁2，如图3(b)所示。将上述2个圆环形磁铁作为相反的偶极子安装在圆柱形轭两端，使检测仪在钢丝绳内部产生大约1.8 T的磁通密度。

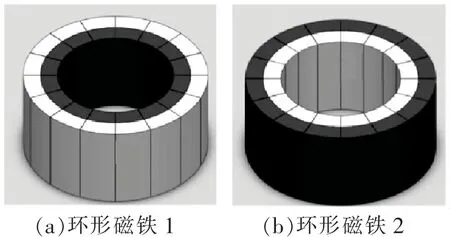
图3 16个平行磁化磁体段组合的径向磁化圆环Fig.3 Radially magnetized circular rings with 16 parallely-magnetized magnet segments

钢丝绳无损检测仪由32个相同的NdFeB磁体段组装而成，且每16个NdFeB磁体段组成一个圆形磁环。组装过程中，各磁铁段的两极之间存在很强的磁力，很难将相邻磁体段组装成环状，而且极易造成磁铁的损坏。若采用手工组装，平行磁化NdFeB磁铁段很容易相互碰撞损坏磁体甚至对人造成伤害。因此，文中设计了一套能够提供磁铁进入磁轭路径的工装夹具，并运用夹具实现了磁体的一体化装配，如图4所示。

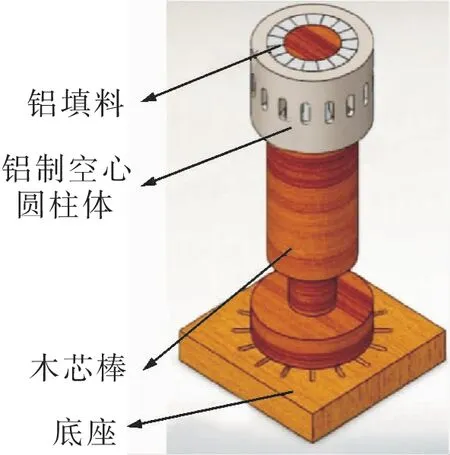
图4 磁体装配Fig.4 A complete result to assemble arc magnets

2.2 新型钢丝绳无损检测仪功能验证

钢丝绳无损检测系统[19]主要由计算机、工作台、采集卡、钢丝绳测试仪、霍尔效应传感器、Labview软件等组成，如图5所示。

图5 钢丝绳无损检测系统Fig.5 Experimental test-rig to test wire rope tester

数据采集卡NI-6024E以每秒30组数据的采样频率，将霍尔效应传感器检测到的模拟信号经PCI接口输入到计算机中，然后通过Labview程序对数据进行分析。用低碳钢直钢丝做钢丝束，人为制作钢丝缺陷并置于试样外层。在检测仪中由于钢丝存在缺陷，磁通会发生泄漏，泄漏的磁通包含3个分矢量分别为钢丝束径向、切向和轴向。其中，局部故障信息包含在漏磁的径向分量中，金属区域的损耗信息包含在漏磁的轴向分量中。因此，可以通过适当改变钢丝绳检测仪中霍尔传感器的方向，来获得LF和LMA信号。

采用灵敏度为-90 mV/mT，量程为0～10 mT的霍尔传感器A采集LF信号。当表面断丝缺陷明显的钢丝绳通过监测仪时，检测信号的时间响应曲线，如图6所示。分析发现：当缺陷明显的钢丝束通过霍尔传感器下方时，信号的幅值上升，缺陷处的最小、最大霍尔电压分别为-80和170 mV，峰值到峰值之间的幅值之差为250 mV。

图6 基于霍尔传感器的LF检测信号Fig.6 LF signal using hall sensor corresponding to broken strand

采用灵敏度为45 mV/mT，量程为0～20 mT的霍尔传感器B采集LMA信号。当有缺陷的钢丝绳通过监测仪时，检测信号的时间响应曲线，如图7所示。分析发现：当含缺陷钢丝束通过霍尔传感器下方时，漏磁信号轴向分量的幅度增大，出现缺陷的最大霍尔电压为-90 mV，偏移电压为-10 mV，相应于缺陷的幅值为80 mV。实验分析表明，新型钢丝绳无损检测仪能够有效的检测钢丝绳的缺陷部位，受损处钢丝绳的漏磁信号幅值变化剧烈，证明该检测仪器的有效性。

图7 基于霍尔传感器的LMA检测信号Fig.7 LMA signal using hall sensor corresponding to broken strand

3 基于BP神经网络的缺陷钢丝绳检测效果对比分析

采用小波变换和BP神经网络，分析新型钢丝绳无损检测仪获取的缺陷钢丝绳漏磁信号，即首先利用小波变换的方法来获得信号特征值，利用BP神经网络来建立损伤识别模型，来完成原始系统和BP神经网络系统中钢丝绳缺陷检测精度的对比分析。

3.1 钢丝绳缺陷信号小波分析

小波分析作为一种信号处理方法，能够有效分析信号的细节，是在时域和频域内分析畸变信号的理论基础[20-22]。设钢丝绳缺陷信号的一个离散样本系列为：f(n)，n=1，2，…，N.令c0(n)=f(n)，则钢丝绳缺陷信号的二进值小波变换为

(5)

式中cj(k)为尺度系数；dj(k)为小波系数；hk-2n为高通滤波器系数；gk-2n为低通滤波器系数。

如果令Hn，k=hk-2n且Gn，k=gk-2n，矩阵H和G满足关系式：H=(Hn，k)和G=(Gn，k)，式(5)表示为

(6)

式中H，G分别为高通和低通滤波器的n次插值，n为正整数。

通过关系式(6)可得

cj(k)=H*cj+1+G*dj+1

(7)

式中H*和G*分别是H和G的关联矩阵。

通过式(7)对获取的原始钢丝绳缺陷信号进行小波重建，用于钢丝绳损伤的定量识别。

3.2 基于BP神经网络的钢丝绳断丝检测模型

BP神经网络模型由3个部分组成，分别为输入层、隐含层、输出层，每层含有不同数量的神经元[23-25]。BP神经网络模型通过比较期望输出值和实际输出值，计算误差值e的标准差σ，当σ小于误差阈值ξ时，输入层与隐含层之间的权重值达到要求，停止训练并得到最终的BP神经网络权值参数。首先在钢丝绳疲劳试验机上制备有效长度为500 mm的25根具有不同断丝缺陷的6×7IWS钢丝绳实验试样，然后运用本研究提出的无损检测仪，任意选取20根含断丝缺陷的钢丝绳进行检测，获取缺陷检测数据用于BP神经网络模型的训练，剩余5根钢丝绳用于获取对比分析数据。

经小波重建后的原始钢丝绳缺陷信号作为输入，设输入层的输入矢量为X=[x1，x2，…，xn]，输入层与输出层的之间的权值为W=[w1，w2，…，wp]，隐含层输出为O=[o1，o2，…，on]，选择激活函数为

(8)

隐含层输出计算公式如下

令隐含层输出O中的元素计算公式为

oi=f(wi×xj+bi)

(9)

令B=[b1，b2，…，bp]，隐含层输出矩阵I计算公式为

O=f(W′×X+B′)

(10)

令输出层权值为Q，Q=[q1，q2，…，qp]，则输出层Y误差E的计算公式为

Y=Q×O

(11)

E=D-Y

(12)

令隐含层与输出层之间的局部梯度G=[g1，g2，…，gn]，输入层与隐含层之间的局部梯度L=(lij)，则权值更新计算公式为

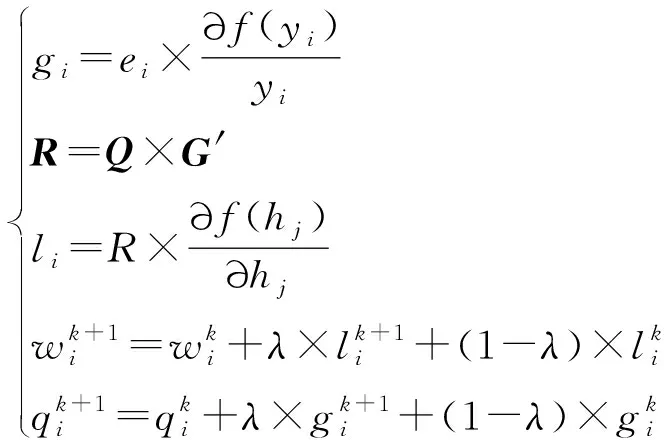
(13)

3.3 实验结果与对比分析

运用BP神经网络对剩余5根待检测的含缺陷钢丝绳进行分析。设学习速度系数为0.05，预期的误差为10-6，实验结果见表1。符号*表示断丝的实际数量是1，但损伤处的漏磁信号太弱而无法被检测识别，斜体加粗表示BP神经网络算法获得的损伤识别结果，具体实验结果对比见表1。

分析表1发现，BP神经网络算法检测的断丝数量相对平均误差为31.5%，断丝位置识别平均误差为22.4%；传统系统的断丝数量相对平均误差为16.7%，断丝位置识别平均误差为10.5%；BP神经网络算法检测精度较传统检测方法提升了13.35%。当断丝数量较少时2种方法的检测精度都较低，随着同一断面附近断丝数量的增加断丝根数和位置检测值越准确。但比较2种方法的检测性能发现，本研究提出的无损检测方法能够在少量断丝情况下更好的识别破损情况。

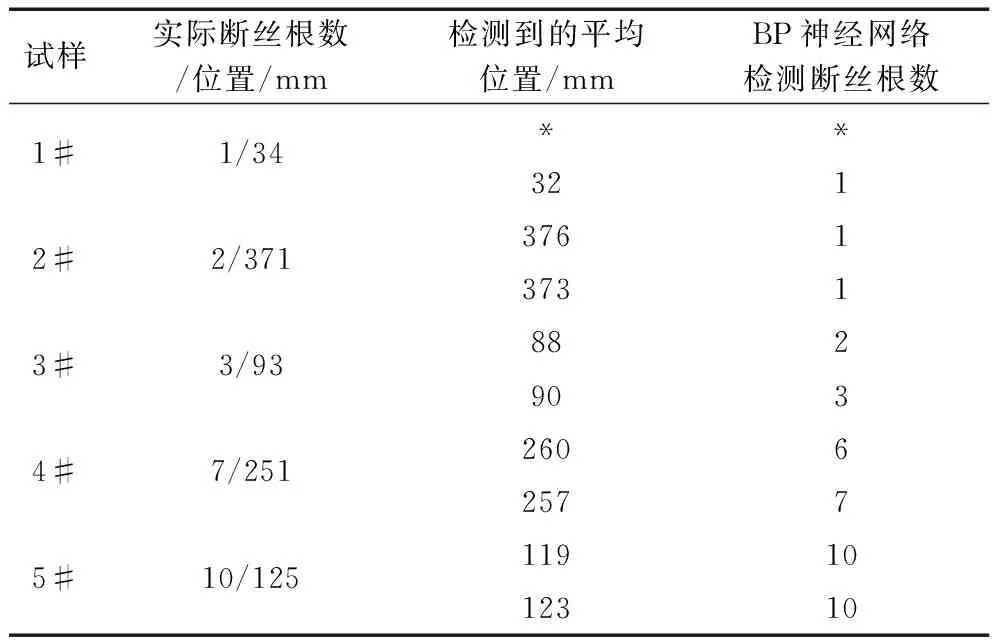
表1 实验数据对比

4 结 论

1)提出一种基于平行磁化NdFeB磁体段的钢丝绳无损检测仪，并验证了其功能的有效性。

2)新型钢丝绳无损检测仪采用的BP神经网络算法，比传统设备的检测算法性能更优。

3)当钢丝绳存在少量断丝时，本检测仪具有更高的诊断精度。