Heston模型下带随机工资的均值-方差DC型养老金计划
李佳奥,常 浩,孙秀秀
(天津工业大学 数学科学学院,天津300387)
养老基金管理是社会保障系统中的一项重要课题.从养老金的给付方式来看,主要分为收益确定型(DB)养老金计划和缴费确定型(DC)养老金计划.在DB型养老金计划中,该计划参与者的养老金给付额是预先确定的,其中不确定性导致的投资风险由养老金管理人来承担.而在DC型养老金计划中,该计划参与者的缴费比率是预先确定的,且养老金的给付额取决于至退休前期间内的缴费及投资收益,其中不确定性导致的投资风险由养老金参与者自己承担.相比之下,DC型养老金计划比较符合养老金计划的管理现状,所以研究和解决各种投资环境下的DC型养老金计划问题具有重要的理论和实践意义.
近年来,许多研究者更关注缴费确定(DC)型养老金的投资问题,并取得了许多重要的研究成果.Vigna和Haberman[1]提出了一类多周期离散时间的养老金投资模型,通过随机动态规划方法得到了最优投资策略.Haberman 和Vigna[2]将Vigna和Haberman[1]的工作拓展到多种风险资产环境下,在三种不同的风险测度下研究了养老金成员的最优投资策略.Deelstra等[3]对随机仿射利率模型下带有最低担保的连续时间养老金投资问题进行了研究,运用鞅方法得到了最优投资策略.Guan和Liang[4]在随机利率和随机波动率框架下研究了带有最低担保的DC型养老金的最优投资策略.Han和Hun[5]在DC养老金计划中考虑了通货膨胀风险的影响,运用动态规划方法得出了最优投资策略.Yao等[6]研究了通胀风险环境下的均值-方差模型,获得了有效策略和有效边界的显性解.常浩等[7]在Yao等[6]市场模型基础上研究了双曲绝对风险厌恶(HARA)效用函数下的最优投资策略,运用随机最优控制和Legendre变换得到了最优投资策略的显式表达式.上述研究成果都假设股票价格波动率是常数,考虑到实际金融市场往往受到许多不确定因素的影响,其波动率往往是随机的.
随机波动率模型比较经典的就是Heston模型,它最早由Heston[8]提出并研究,该模型假设风险资产(股票)的收益率和波动率都是随机的,因而更符合实际金融市场.近年来,许多学者对Heston模型下的DC型养老金问题进行了研究,得到许多重要的研究成果.林祥和杨益非[9]研究了终端财富期望指数效用最大化的最优投资策略问题.肖建武和尹希明[10]针对待遇预定制养老金的资产组合管理问题,应用最优控制理论和Legendre变换,得到了养老基金管理的最优资产配置和最优缴费水平.常浩等[11]对随机利率和随机波动率环境下的DC养老金投资问题进行了研究,得到了最优投资策略的显式解.上述问题均假设缴费率是常数.实际上,养老金成员的缴费率与其工资水平有关,而工资水平在养老金累积阶段往往是随机变化的,因而研究和解决带有随机工资的养老金投资问题具有重要的理论价值和实践意义.
养老基金的投资是一项长期投资,一般需要20~40年,在这么长的时间里养老金计划持有人的工资收入一般是随机变化的.近年来,很多学者对带有随机工资的养老金投资问题进行了研究,取得了比较好的研究成果.张初兵等[12]和 Zhang等[13]对常数方差弹性(CEV)模型下带有随机工资的DC型养老金投资问题进行了研究,分别得到了幂效用和指数效用下最优投资策略的闭式解.Li等[14]进一步在均值-方差准则下研究了DC型养老金计划的时间一致性投资策略和有效边界.这些研究的DC养老金投资问题集中在CEV模型下,而本文是在Heston模型下研究带有随机收入的DC养老金问题.伍慧玲和董洪斌[15]在均值-方差准则下研究了带通货膨胀和随机收入的离散时间多期DC型养老金计划.Wang和Li[16]考虑了利率风险和波动风险,假设养老金计划持有人是模糊厌恶的,研究了一种带有随机缴费情形的DC型养老金计划问题,得到了幂效用函数下的鲁棒最优投资策略.Zeng等[17]假设养老金计划持有人是模糊厌恶的,在Heston随机波动率模型下研究了一种带有随机工资和衍生品的DC型养老金投资问题.
很多学者在研究养老金最优投资问题时,目标都是使终端时刻财富的期望效用达到最大,例如林祥和杨益非[9]和Wang和Li[16]等,没有考虑到终端时刻财富的方差.而方差代表风险,因此同时考虑期望和方差使研究变得更有意义.本文假设工资收入是随机的,在Heston随机波动率模型下研究了一种带有随机工资的DC型养老金投资问题,建立了一种均值-方差模型.运用拉格朗日乘子法和拉格朗日对偶定理得到了有效策略和有效边界的闭式解,并给出数值算例分析了波动参数和工资参数对有效策略和有效边界的影响.
1 养老金投资模型
令(Ω,F,{Ft}t∈[0,T],P)为完备概率空间,其中Ω是实空间,P是概率测度,{Ft}t∈[0,T]表示t时刻的信息流,且t时刻的任何决策都依赖这些信息.[0,T]表示固定的有限投资期长,其中T表示养老金计划成员的退休时刻.本文假定金融市场是连续、无摩擦的且没有交易成本和税收,金融资产允许卖空、且可以以无风险利率进行借贷.假设金融市场包括两种可以连续交易的金融资产:一种无风险资产和一种风险资产.
无风险资产可看作是银行账户,其t时刻的价格记为S0(t),则S0(t)满足下面的微分方程:
(1)
其中:参数r>0是无风险利率.
风险资产可看作是股票,其t时刻的价格记为S1(t),本文假设S1(t)满足下面的Heston随机波动率模型:
S1(0)=s1>0;
(2)
L(0)=l0>0;
(3)
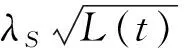
因为养老基金投资是一项长期投资,一般需要20~40 a,在这么长的时间里养老金计划持有人的工资水平一般是一个随机过程,时刻t的工资水平记为C(t),则可假设C(t)满足下面的随机微分方程:
(4)
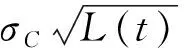
一般来说,养老金计划持有人的缴费率和其工资水平呈正比,我们假设养老金的缴费率是以kC(t)的形式连续地流入养老金个人账户.定义π(t)和X(t)-π(t)分别是投资于股票和无风险资产的资金数量,其中X(t)为养老金账户持有人在时刻t的财富.那么财富过程X(t)可以表示为
dX(t)=(X(t)r+π(t)λSL(t)+kC(t))dt+
(5)
其中:养老金的初始财富为X(0)=x0>0.
定义1(可行策略)一种策略π(t)称为可行的,假如π(t)满足如下条件:
(i)π(t)是Ft-可测的,且满足

(iii)对于任意的初始点(t0,l0,c0,x0),方程(5)的解是唯一的.
本文主要研究累积阶段DC型养老金计划的最优投资策略.假设所有可行策略π(t)形成的集合为Γ,计划持有人的目标是获得一种最优投资组合π(t),使得对于给定的期望财富水平E(X(T))=K,∀K∈,能够最小化持有人所承担的风险
Var(X(T))=E(X(T)-E(x(T)))2=
E(X(T)-K)2
(6)
从投资组合选择的角度来看,上述目标可以归纳为下面的均值-方差模型:
s.t.E(X(T))=K.
(7)
2 最优投资组合
本节应用随机动态规划原理和变量替换方法求解问题(7)的最优投资策略.
引入拉格朗日乘子2λ∈,我们获得如下的目标函数:
E(X(T)-(K-λ))2-λ2,
(8)
令γ=K-λ,我们获得如下的目标函数:
(9)
由拉格朗日对偶定理可得问题(7)和(9)之间的关系如下


(10)
对于固定的常数γ和K,问题(9)等价于下列问题
(11)
定义价值函数J(t,l,c,x)如下
X(t)=x,C(t)=c),
(12)
其中:边界条件为J(Tml,c,x)=(x-y)2
根据随机动态规划原理,假设J(t,l,c,x)∈1,2,2,2([0,T]×+×+×+),则J(t,l,c,x)满足下列Hamilton-Jacobi-Bellman (HJB)方程:
(13)
其中:边界条件为J(T,l,c,x)=(x-γ)2,且A是一种变分算子,由下式确定:
Aπ(t)J(t,l,c,x)=Jt+(rx+π(t)λSl+kc)Jx+
α(δ-l)Jl+(μc+cσCλSl)Jc+
π(t)σLlρJlx+cσCσLlρJlc+π(t)clσCJcx,
(14)
其中:Jt,Jx,Jl,Jc,Jxx,Jll,Jlx,Jcx,Jlc分别表示J(t,l,c,x)关于变量t,l,c,x的一阶和二阶偏导数.
由极值的一阶条件,可得
(15)
将式(15)代入式(14),得到
Jt+(rx+kc)Jx+α(δ-l)Jt+
(16)
由边界条件J(T,l,c,x)=(x-γ)2,我们猜想方程的解如下:
J(t,l,c,x)=f(t,l)(x-D1(t)-D2(t)c)2,
f(T,l)=1,D1(T)=γ,D2(T)=0,
(17)
计算J(t,l,c,x)各阶偏导数如下:
Jt=f1(x-D1(t)-D2(t)c)2-
Jx=2f(2-D1(t)-D2(t)c),Jxx=2f,
Jl=fl(x-D1(t)-D2(t)c)2,
Jll=fll(x-D1(t)-D2(t)c)2,
Jc=-2f(x-D1(t)-D2(t)c)D2(t),
2fl(x-D1(t)-D2(t)c),
Jcx=-2fD2(t),Jlc=
-2f(x-D1(t)-D2(t)c)D2(t).
(18)
将式(18)代入式(16),并应用式
rxx=2rf(x-D1(t)-D2(t)c)x=
2rf(x-D1(t)-D2(t)c)2+2rf(x-D1(t)-D2(t)c)(D1(t)+D2(t)c).
得到
分离变量后,得到下列三个方程:
(19)
(20)
(21)
假设方程(19)的解的形式如下:
f(t,l)=eA1(t)+A2(t)l,A1(T)=0,A2(T)=0
则A1(t)和A2(t)满足如下方程:

时,则有Δ>0,此时A1(t)和A2(t)由下列两式确定:
A1(t)=2r(T-t)+αδm2(T-t)+
(22)
(23)

解方程(20)和(21),可得
D1(t)=γe-r(T-t),
(24)
(25)
进一步可以得到:
定理1 对于固定的常数γ和K∈,问题(9)和(11)的最优投资策略可表达为:
π*(t)=(X(t)-D1(t)-D2(t)C(t))
(-λS-σLρA2(t))+σCC(t)D2(t),
(26)
且价值函数可表达为
J*(t,l,c,x)=f(t,l)(x-D1(t)-D2(t)c)2
(27)
其中:f(t,l)=eA1(t)+A2(t)l,且A1(t),A2(t),D1(t)和D2(t)分别由式(22),(23),(24)和(25)给出.
3 有效边界
本节应用拉格朗日对偶定理推导问题(7)的有效边界.
根据定理1,问题(11)的价值函数为:
J*(t,l,c,x)=f(t,l)(x-D1(t)-D2(t)c)2,
则问题(11)的最小值可写作:
J*(0,l0,c0,x0)=f(0,l0)(x0-D1(0)-D2(0)c0)2
=f(0,l0)(x0-γe-γT-D2(0)c0)2.
因此,问题(9)的最小值可表达为:
(f(0,l0)e-2rT-1)γ2+2(K-Bf(0,l0)e-rT)γ+
B2f(0,l0)-K2,
(28)
其中:B=x0-D2(0)c0.
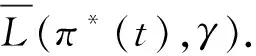
(29)
得到
(30)
综上所述,可以得到问题(7)的有效策略和有效边界如下:
定理2 对于给定的常数K∈,问题(7)的有效策略可表达为
π*(t)=(X(t)-D1(t)-D2(t)C(t))
(-λS-σLρA2(t))+σCC(t)D2(t),
(31)
且有效边界可表达为
(E(X(T))-BerT)2.
(32)
其中:A1(t),A2(t),D1(t),D2(t)分别由式(22),(23),(24)和(25)给出.
备注1. 由定理2,可以得到如下结论:(i)有效策略π*(t)不仅依赖于参数α,σL,μ和σC,而且依赖于参数λS,ρ和T;(ii)有效策略π*(t)依赖于参数波动系数σC,而有效边界Var(X(T))不依赖于参数波动系数σC;(iii)有效策略π*(t)不再是时间t的有界确定函数,而是依赖于瞬时财富水平X(t)和瞬时工资水平C(t).
备注2. 根据式(32),可以得到风险与收益的关系如下:
其中:σ(X(T))表示标准差.从中可以得出如下结论:(i)有效边界在均值-标准差平面内仍然是一条直线;(ii)当σ(X(T))=0,我们可以得到E(X(T))=(x0-D2(0)c0)erT.
同时,根据定理2,还可以得到下列三种特殊情形.

D2(t)C(t))+σCC(t)D2(t).
同时,有效边界(32)退化为
其中:D1(t)和D2(t)分别由式(24)、(25)给出.

(-λS-σLρA2(t)),
同时,有效边界(32)退化为
其中:A1(t)和A2(t)分别由式(22)、(23)给出.
特例3.如果波动率和工资均为常数,即μ=σC=α=δ=σL=0,记L(t)=l0,C(t)=c.则有效策略(31)退化为
同时,有效边界(32)退化为
4 算例分析
本节运用算例分析波动率参数和工资参数对有效策略和有效边界的影响.我们假设金融市场包括一种无风险资产和一种风险资产.不失一般性,假定参数取值如下:
α=6.5,δ=0.035,l0=0.25,r0=0.05,ρ=-0.65,λS=1.5,T=1,x0=100,c0=25,μ=0.06,k=0.15,σL=0.45,σC=0.8,K=130.
4.1 波动率参数和工资参数对有效策略的影响
运用定理2的结论,本文给出了波动率参数和工资参数对有效策略的影响,如图1、2所示.从中可以得出如下一些结论:
1)π*(t)关于参数α递增,而关于参数σL递减 .将方程(3)两边取期望后可得dE(L(t))=(αδ-αE(L(t)))dt,解出E(L(t))=δ+(l0-δ)e-αt,对其两边参数α求导后可得E′(L(t))=-te-αt(l0-δ),当l0<δ(符合实际情况),E(L(t))是递增函数,这使得股票的期望收益率增加,这时投资于股票的数量将增加,而投资于无风险资产的数量将减少;另一方面,在股票的波动模型中,当参数σL增加时,意味着方差的波动风险将增大,为了规避风险,投资人将减少投资到股票的资金数量.
2)π*(t)关于参数ρ递增,而关于参数λS递减.当相关系数ρ从-0.7增加到-0.1时,其负相关性越弱.这说明当波动风险与股市风险处于负相关时,波动风险就越大,股市风险越小,这时投资人应将较多的资金投资于股票.另一方面,当参数λS递增时,工资的增长率随之递增,这导致养老金持有人的缴费率越来越大,财富的增长使得投资人变得比较保守,从而投资到股票的资金数量越来越少.

图1 波动参数λS、ρ、α和σL对π*(t)的影响
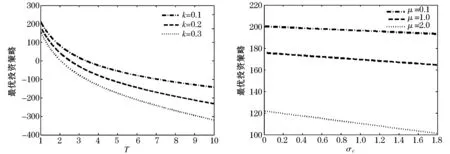
图2 工资参数μ、σC和k对π*(t)的影响
3)π*(t)关于参数μ和σC均递减.当参数μ的值增大时,期望工资水平会随之增加,这使得养老金持有人的缴费率随之增加.缴费率的增长导致财富水平的增长,较高的财富水平将使得投资人变得比较保守,比较愿意将更多资金投资到无风险资产上,而将较少的资金投资到股票上.另一方面,当参数σC的值增大时,工资波动风险将随之增加,这将导致股市波动风险也随之增加.为了规避风险,投资人应将较少的资金投资于股票,而将更多的资金投资于无风险资产.
4)π*(t)关于参数T和k均递减.随着参数k的增加,养老金持有人的缴费率随之增加,这将导致养老金账户有更多的积累,这时的投资人将变得比较保守,为规避风险,投资人比较愿意将更多的资金投资于无风险资产,而将较少的资金投资于股票.另一方面,由于T代表养老金成员的退休时刻,当T增加时,这意味着养老金成员的退休年龄在延迟.考虑到投资有风险等因素,为了确保退休后养老金的按时足额发放,投资人应将较多资金投资于无风险资产,而将较少的资金投资于股票.
4.2 波动率参数和工资参数对有效边界的影响
运用定理2的结论,本文给出了波动率参数和工资参数对有效边界的影响,如图3、4所示.我们可以得出如下一些结论:
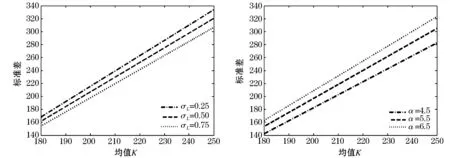
图3 波动参数α和σL对有效边界的影响
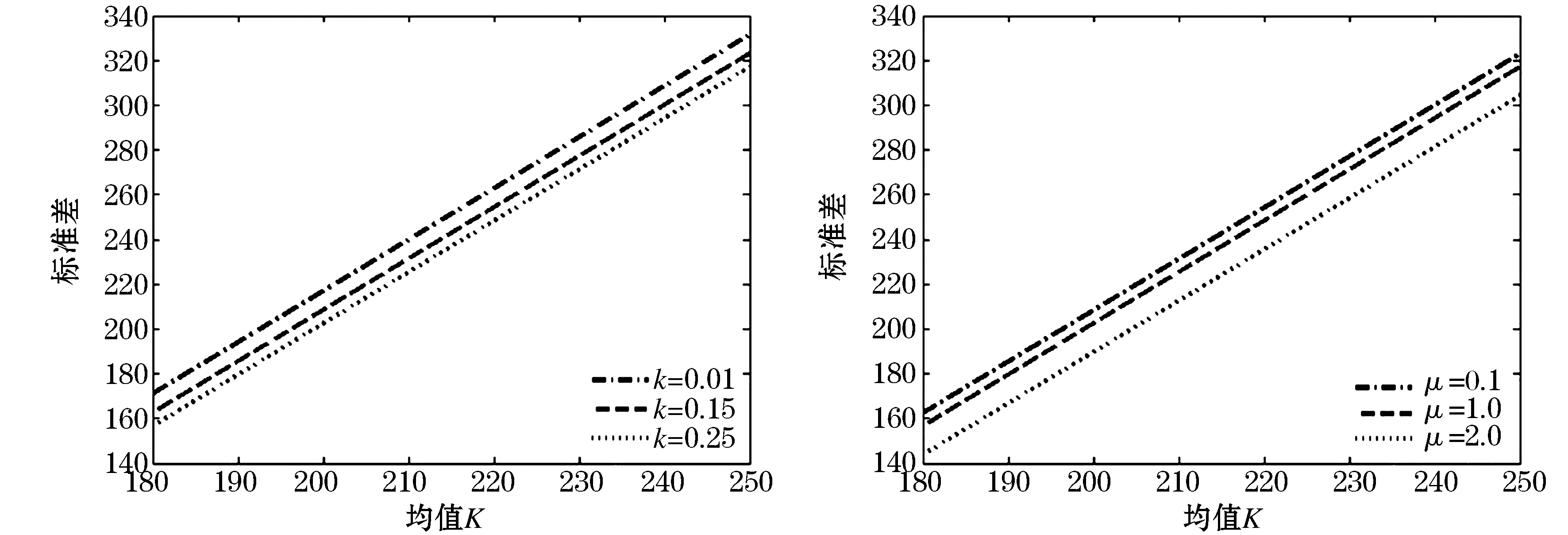
图4 工资参数μ和k对有效边界的影响
1) 对于给定的期望收益E(X(T))=K,标准差σ(X(T))关于参数α递增;换句话说,对于给定的风险水平σ(X(T)),期望收益E(X(T))关于参数α递减.在随机波动率方程(5)中,参数α代表方差波动率的均值回复速度,参数α越大,则说明方差的波动率回归到均值水平的速度越快,这意味着波动率越大,即风险越高.
2) 对于给定的期望收益E(X(T))=K,标准差σ(X(T))关于参数σL递减;或者说,对于给定的风险水平σ(X(T)),期望收益E(X(T))关于参数σL递增.当参数σL的值增大时,虽然方差波动率是增大的,但由于股市波动与方差波动呈现一种负相关关系,因而,股市风险是递减的,即风险水平σ(X(T))也是递减的.
3) 对于给定的期望收益E(X(T))=K,标准差σ(X(T))关于参数μ递减;或者说,对于给定的风险水平σ(X(T)),期望收益E(X(T))关于参数μ递增.当参数μ的值增大时,由4.1知投资于股票的资金数量将随之减少,因而,投资人面临的风险也随之减少.
4) 对于给定的期望收益E(X(T))=K,标准差σ(X(T))关于参数k递减;或者说,对于给定的风险水平σ(X(T)),期望收益E(X(T))关于参数k递增.当参数k的值增大时,养老金持有人的个人账户虽然有更多的积累,但为了规避风险,养老金持有人投资于股票的资金数量将随之减少,因而,投资人面临的风险也随之减少.
4.3 一些比较
为了更准确的分析随机波动率与随机工资对有效策略和有效边界的影响,本节给出了随机波动率下与常数波动率下、随机工资下与常数工资下、随机波动率与随机工资下和常数波动率与常数工资下有效策略和有效边界的一些比较,即根据定理2与特例1~3的相关结论,我们给出了一些比较,如图5~7所示,从中可以得出以下结论:

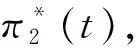
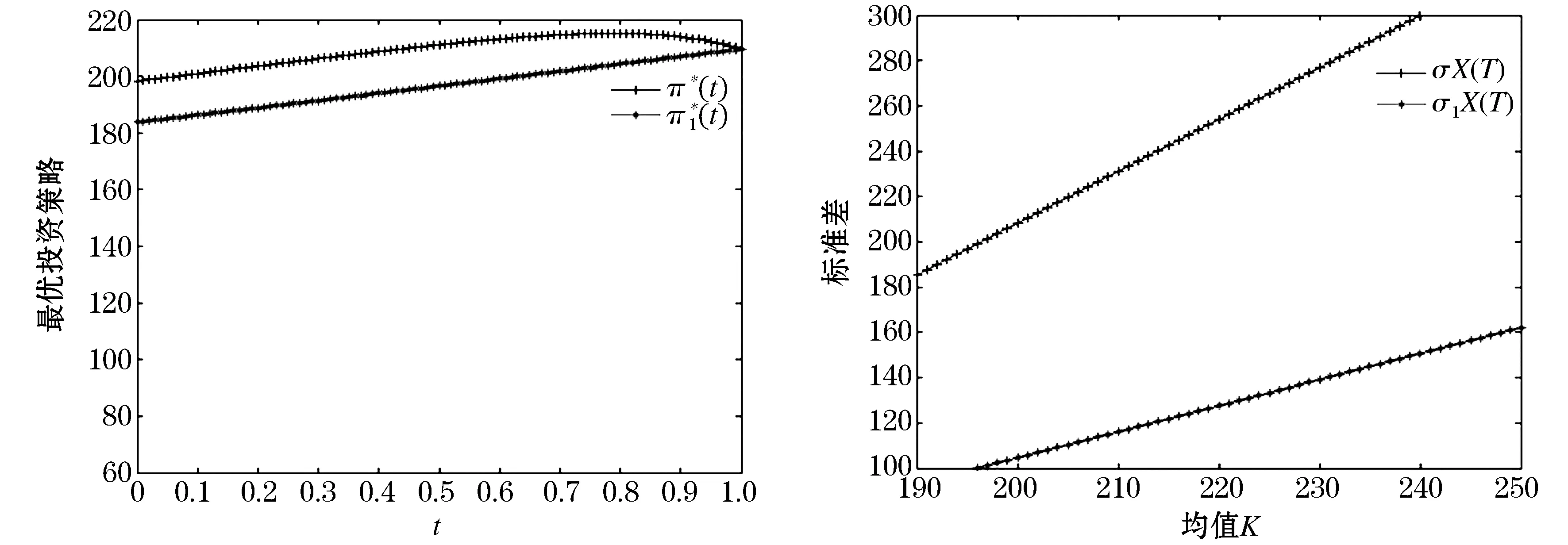
图5 随机波动率下和常数波动率情形下有效策略和有效边界的比较

图6 随机工资下和常数工资情形下有效策略和有效边界的比较

图7 常数工资与常数波动率下和随机工资与随机波动率下有效策略和有效边界的比较

5 结 语
在养老金累积阶段,实现养老金的保值增值有效方法之一是将养老金投资于金融市场,但是投资面临着风险,如何在最大化投资收益的同时最小化投资风险是该课题的重要研究内容.本文假设股票价格服从Heston随机波动率模型,养老金持有人的工资是随机变化的,从而导致缴费率也是随机变化的,建立了一种均值-方差模型,目的是了解基金管理人风险和收益相权衡的决策过程.运用随机动态规划原理和拉格朗日对偶原理,我们得到了有效策略和有效边界的显式解.算例分析了波动率参数和工资参数对有效策略和有效边界的影响.研究表明:有效边界在均值-标准差平面内仍然是一条直线,有效策略仅依赖于瞬时工资水平,而有效边界不依赖于工资水平和波动率水平.
通过数值算例,得到以下结论:1)当均值回复速度α增大时,π*(t)增大,当波动系数σL增大时,相应地π*(t)减小;当λS增大时,有效策略π*(t)随之减小;当相关系数ρ增大时,有效策略*(t)随之增大;2)工资水平的期望增长率μ或波动率系数σC越大,投资到股票中的资金数量π*(t)越小;投资期限T或缴费率k越大,有效策略π*(t)越小;3)对于给定的期望收益水平,均值回复速度α越大,投资人承担的风险σ(X(T))越大;参数σL或μ或k越大,风险水平σ(X(T))越小;4)和常数波动率相比,随机波动率环境下投资人需要将更多资金投资于股票,因而需要承担更多的风险;和常数工资相比,随机工资下投资于股票的资金数量较多,但承担的风险是相同的,即工资的随机变化虽然导致缴费率的随机变化,但并没有增加投资人的风险.

