混合动力汽车耦合系统工作模式分析与动态特性研究

秦鹏飞，颜长征，王若璜，秦 燕

(重庆车辆检测研究院有限公司 国家客车质量监督检验中心，重庆 401122)

混合动力汽车(HEV)能够利用多个动力转化装置的不同耦合关系实现多种工作模式，从而获得最佳的综合性能[1-6]。目前，国内有许多学者对混合动力耦合系统进行了研究[7-8]，但对混合动力耦合机构动态特性的研究却很少。事实上，很多动力耦合设计方案在实际试验和使用中产生了很大的振动，根本无法真正投产。因此，在研究工作模式的基础上，对混合动力汽车耦合机构的动态分析同等重要。

1 耦合系统工作模式分析

本文分析一种基于CVT的并联式单行星排动力耦合系统，如图1所示。其中发动机通过离合器1与行星架6连接，通过离合器2与太阳轮5相连；电机与太阳轮5相连；行星架6中装有制动器3，齿圈7上装有制动器4，动力通过中间齿轮8传至CVT 9的主动轮。

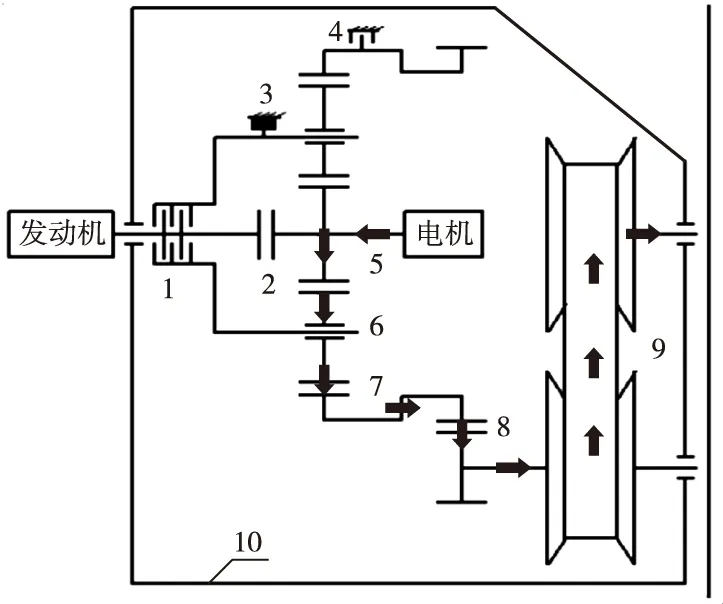
图1 耦合系统结构及纯电动模式功率流示意图

相比于双行星齿轮机构、双电机形式的动力耦合系统，该方案结构紧凑、控制简单，有利于降低成本，且CVT扭矩容量要求低，无低负荷工作状态，传动效率高。通过控制系统中离合器与制动器的接合与分离，可以实现混合动力系统的多种工作模式。

1) 纯电动驱动模式。当车辆处于起步或市区堵车工况下，为避免发动机工作在低效区，采用纯电动驱动。该模式下，图1中的离合器1、离合器2都处于分离状态，制动器3接合，电机根据负载输出功率。纯电动驱动模式下的功率传递路线：电机→太阳轮5→行星架6→齿圈7→中间齿轮8→CVT 9→车轮，其功率流向如图1所示。

2) 发动机单独驱动模式。当车辆以较高车速行驶，所需的功率处于发动机的高效工作区，此时汽车工作在发动机单独驱动模式。该模式下，图1中的离合器1和离合器2都接合，行星齿轮机构5、6、7自锁，作为一个整体运转，电机空转。该模式下的功率传递路线：发动机→行星齿轮机构5、6、7→中间齿轮8→CVT 9→车轮。

3) 行车充电模式。当行车负载较小，达不到发动机的最佳工作负荷时，在发动机运行的同时，电机以发电模式运行，增加发动机的负荷，以提高其效率，以改善经济特性和排放，同时维持电池电量平衡。该模式下，图1中的离合器1和离合器2都接合，行星齿轮机构5、6、7自锁，电机反转发电。该模式下的功率传递路线是在行星齿轮机构处分流，一条路线：发动机→行星齿轮机构5、6、7→电机；另一条路线：发动机→行星齿轮机构5、6、7→中间齿轮8→CVT 9→车轮。

4) 混合驱动模式。当车辆在大负荷工况下行驶，发动机或电机单独驱动无法满足行车功率需求时，两者将同时输出功率，联合驱动。根据不同行车工况，混合驱动分为电机助力和电机调速两种模式：

①电机助力。当汽车在爬坡、超车或加速等大负荷工况下行驶，所需驱动功率远大于发动机的最优功率时，电机补充动力。该模式下，图1中的离合器1和离合器2都接合，行星齿轮机构5、6、7自锁，电机正转输出功率。两者的功率在行星齿轮机构5、6、7上实现耦合。该模式下的功率传递路线：发动机和电机→行星齿轮机构5、6、7→中间齿轮8→CVT 9→车轮。

②电机调速。当汽车高速巡航时，为保持车速，并使得发动机处于稳定工作状态，可利用电机调速。该模式下，图1中的离合器1接合，离合器2分离，电机正转输出较小功率，用于调速。该模式下的主要功率传递路线：发动机→行星架6→齿圈7→中间齿轮8→CVT 9→车轮。

5) 再生制动模式。减速过程中，可利用电机反拖进行动力回收，将车辆动能转化为电能存储至动力电池中。根据减速前的行车状况，再生制动分为有发动机拖动再生制动(B挡)和无发动机拖动再生制动(D挡)两种形式：

①发动机拖动制动(B挡)。当汽车下陡坡时，采用电动机和发动机联合制动。该模式下，图1中的离合器1和离合器2都接合，行星齿轮机构5、6、7自锁，作为一个整体运转。由于汽车行驶惯性，带动行星齿轮机构运转，一部分功率用于克服反拖发动机的阻力；另一部分功率用于电机发电储存至动力电池。B挡制动模式功率传递路线：车轮→CVT 9→中间齿轮8→行星齿轮机构5、6、7→发动机和电机→动力电池。

②无发动机拖动制动(D挡)。该模式可增大能量回收效率。图1中的离合器1和离合器2都分离，制动器3接合，行星架6与机架10连接，制动器4分离。该模式的功率传递路线：车轮→CVT 9→中间齿轮8→行星齿轮机构5、6、7→电机→动力电池。

2 耦合系统动态特性分析

2.1 系统动力学模型建立

整个耦合系统主要包括行星齿轮机构和CVT。由于CVT通常采用成熟产品，不单独开发，所以对于新开发的耦合系统的动态特性主要取决于行星齿轮机构的结构与参数。因此，本文仅研究耦合系统中行星齿轮机构的动态特性。基于集中质量参数法[9]建立以行星架6的转速ωc为动坐标的行星齿轮机构的动力学模型，如图2所示。

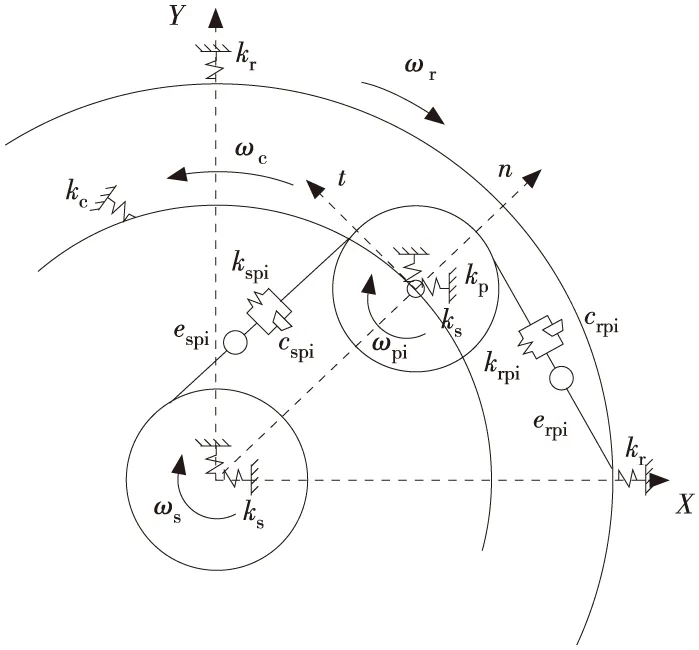
图2 耦合系统动力学模型

其中ks为太阳轮5的支撑刚度，kc为行星架6的扭转刚度，kr为内齿圈7的支撑刚度，kp为行星轮的支撑刚度。kspi、cspi、espi分别为太阳轮与行星轮的啮合刚度、啮合阻尼和啮合误差，krpi、crpi、erpi分别为内齿圈与行星轮的啮合刚度、啮合阻尼和啮合误差。行星齿轮机构力学模型中共有(7+3N)个自由度(N表示行星轮数目)。该机构的广义坐标：

X=(εs,xs,ys,εpi,tpi,npi,εr,xr,yr,εc)T

式中：εs、εpi、εr分别为太阳轮、行星齿轮和内齿圈沿啮合线的微位移；xs、xr分别为太阳轮和内齿圈在水平方向的微位移；ys、yr分别为太阳轮和内齿圈在竖直方向的微位移；tpi、npi为行星齿轮在切向和径向的微位移；εc为行星架沿切向的微位移。

2.2 系统动力学平衡方程

齿轮的制造误差和安装误差所造成的偏心误差是齿轮传动系统产生振动的主要因素[10]。各齿轮的偏心误差对齿轮啮合的激励表现为在啮合线方向上的位移激励，研究时将其转化到齿轮副啮合线上，则行星轮与太阳轮和内齿圈的等效啮合误差分别为espi、erpi：

espi=Espisin(ωt+θspi)-Episin(ωpic+θpi+∂)-
Essin(ωsct+θs-φi+∂)

erpi=Erpisin(ωt+θrpi)-Episin(ωpic+θpi+β)+
Ersin(ωrct+θr-φi+β)

式中：Espi、θspi分别为行星轮与太阳轮的齿频误差和初相位，Erpi、θrpi分别为行星轮与内齿圈的齿频误差和初相位；Epi、Es、Er分别为行星轮、太阳轮和内齿圈的偏心误差，其初相位分别为θpi、θs、θr；ω表示啮合齿频，ωpic、ωsc、ωrc分别为行星轮、太阳轮和内齿圈相对于行星架的转速；∂、β分别为行星轮与太阳轮和内齿圈的啮合角；φi表示共N个行星轮中第i个行星轮相对于第一个行星轮的位置角，φi=2π(i-1)/N。

εpi、εs、xs、ys、tpi、npi、espi在啮合线上的等效合微位移为ζspi，εpi、εr、xr、yr、tpi、npi、erpi在啮合线上的等效合微位移为ζrpi，则：

ζspi=εs-εpi-tpicosα-npisinα+xssin(α-φi)+
yscos(α-φi)-espi

ζrpi=εr-εpi-tpicosβ-npisinβ+xrsin(β+φi)+
yrcos(β+φi)-erpi

从而可得到行星轮分别与太阳轮和内齿圈沿啮合线方向的啮合力Fspi、Frpi，以及啮合阻尼力Dspi、Drpi：

Fspi=kspi·ζspi,Frpi=krpi·ζrpi

根据Lagrange方程，将作用在各个构件上的惯性力、阻尼力与外部激励力组成平衡力系，可以推导出行星机构各个部件的振动微分方程。

太阳轮平衡方程：

(1)

行星轮平衡方程：

(2)

内齿圈平衡方程：

(3)

行星架平衡方程：

(4)

式(1)～(4)中:Ms、Mp、Mr、Mc分别为太阳轮、行星轮、齿圈、行星架的等效质量(M=J/r2，J为相应构件的转动惯量)；ms、mp、mr分别为太阳轮、行星轮、齿圈的(平移)质量；rs、rr分别为太阳轮和内齿圈的基圆半径；rc为行星架的当量基圆半径；Tm、Te分别为电动机和发动机的输入扭矩；Tout为齿圈输出扭矩。

将方程(1)～(4)整理成矩阵形式：

(5)

式中：M、X、C、K(t)、F分别为行星齿轮机构的广义质量矩阵、广义坐标位移矩阵、阻尼矩阵、时变刚度矩阵以及外载荷矩阵，其中外载荷矩阵包括电机扭矩、发动机扭矩、啮合力、啮合阻力，而啮合力与啮合阻力是由偏心误差Epi等引起的。

2.3 系统动态特性

在混合动力汽车各种工况中，混合驱动模式下的行驶功率最大，发动机、电动机输出转速及扭矩较大，造成动力耦合器产生较大的振动。因此，此处对汽车处于混合驱动模式下的行星齿轮机构的动态特性进行分析。该工况下，发动机输入转速n=6 000 r/min，输入功率P=75 kW，电动机输入转速n=8 000 r/min，输入功率P=60 kW，可通过P=T·n/9 549的关系式计算出相应的扭矩。齿轮主要参数如下：太阳轮齿数zs=23，行星轮齿数zp=18，内齿轮齿数zr=58；模数mn=1.75；压力角α=20°；总行星轮个数N=3。在传动软件KissSoft中，输入以上齿轮参数即可获得行星机构中的齿频误差及初相位。太阳轮与行星轮的等效啮合刚度为5.06×108N/m，啮合阻尼为5.06×103，行星轮与内齿圈的等效啮合刚度为5.70×108N/m，啮合阻尼为5.06×103；太阳轮、行星轮与内齿圈的径向支承刚度分别为1×1010N/m；同时考虑各齿轮的偏心误差为10 μm，齿频误差为5 μm。

采用数值分析方法[11-12]，在MATLAB软件中求解微分方程(5)，可得到行星轮系中各个构件在水平、竖直、啮合线方向的位移。其中，沿啮合线方向上的位移较大，各构件沿啮合线方向的位移，即扭振位移，如图3～6所示。由图可知，扭振位移随啮合周期重复波动，其中齿圈扭振位移的振幅最大，达到0.2 mm。这是因为发动机、电机输入的功率，通过太阳轮、行星轮的传递，在齿圈处耦合，形成了系统中最大的扭矩。因此，行星齿轮机构中齿圈的振动将对车辆的振动产生重大的影响。

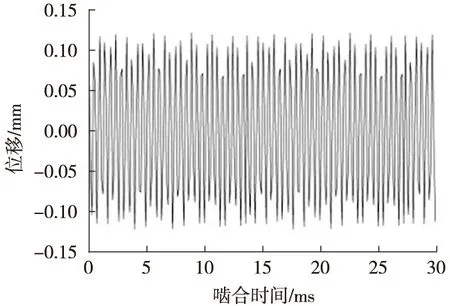
图3 太阳轮扭振位移曲线

图4 行星轮扭振位移曲线

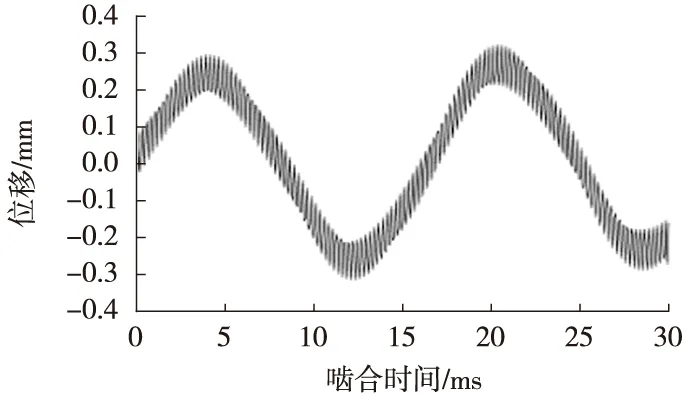
图5 齿圈扭振位移曲线

图6 行星架扭振位移曲线

3 结束语

本文对一种混合动力汽车动力耦合机构的工作模式进行了详细的分析，并针对系统中的行星齿轮机构建立了动力学模型、求解了其动态特性。结果表明，承受最大扭矩的齿圈产生了较大振动。如何通过优化齿轮参数和结构，以改善系统的动态特性值得进一步研究。