基于动态规划的Needleman-Wunsch双序列比对算法的分析与研究*
甘秋云
(福州理工学院计算与信息科学学院,福建 福州 350014)
1 引言
随着人类各项基因组计划的逐渐实施,核酸和蛋白质的数据正呈现指数级增长,如何处理分析庞大的生物数据,成为当今科学家所面临的一项重大的挑战,生物信息学也随之发展。生物信息学是一门将生物学、计算机科学、数学及其他处理技术相结合的学科,在生命科学研究中占有重要的地位,它的主要任务是探寻高效的研究和分析生物数据的工具,找出具有重要价值的生物学知识,从而分析和探究生物数据所蕴含的信息,进一步理解生命和进化关系[1]。
序列比对是生物信息学研究的主要课题之一,是运用特定的算法分析2条或多条序列之间的相似性的过程。通过序列比对,可以判断2条基因序列之间是否具有相似性,进而分析同源性,推导生物进化的过程,它对于发现生物序列中的功能、结构和进化信息都具有重要的意义[2]。
当今,序列比对算法有很多,主要类型有:双序列比对和多序列比对、全局比对和局部比对。典型的全局比对算法是Needleman-Wunsch算法,局部比对算法为Smith Waterman算法。双序列比对算法中较成熟的是基于动态规划的算法,和由此提出的FASTA(FAST-ALL)和BLAST(Basic Local Alignment Search Tool)算法;多序列比对主要用于识别多条序列的公共特征,主要有clustalW算法、MAFFT(Multiple Alignment using Fast Fourier Transform)算法和MUSCLE(Multiple Protein Sequence Alignment)算法[3]。
由于不同的比对算法具有不同的空间复杂度和时间复杂度,因此在序列比对过程中,数据的存储和比对结果的精准度也不同,面对呈指数级增长的生物数据,如何研究并设计一种高效精准的DNA序列比对算法,已经成为生物信息学面临的挑战之一。
2 Needleman-Wunsch算法原理
动态规划是用来求解最优化问题的,并且每一部分的解都是最优的。Needleman-Wunsch算法是由Needleman和Wunsch在1970年提出的,也是沿用至今的序列比对算法之一[4]。
Needleman-Wunsch算法主要通过迭代的方式求出2条序列之间的比对得分,并将得分存入二维得分矩阵M中,运用动态规划算法,采用回溯技术,从而找到序列比对的最佳路径,即序列比对的最优结果。
实现Needleman-Wunsch算法主要有3个步骤:(1)建立一个二维得分矩阵,根据特定的打分规则(采用迭代方式和空位罚分规则)初始化矩阵;(2)通过得分规则和计算公式,计算二维矩阵每个单元Mi,j的相似性得分,并填充矩阵;(3)利用回溯方法找出比对的最佳路径,即最佳比对结果[5]。
(1)假设2条序列分别为序列S和序列T,其碱基序列如表1所示。

Table 1 S and T sequences
本文使用最简单的打分规则,如下所示:
(1)
其中,k1是序列碱基匹配得分,k2是错配时的得分,k3是插入空位的情况得分,Si表示序列S中第i个碱基符号,Tj表示序列T中第j个碱基符号。即:
(2)
(2)计算填充得分矩阵。
根据Mi,j计算公式,通过水平、垂直和对角线3个方向递归计算Mi,j的值。其中,对角线方向的Mi-1,j-1得分加上打分函数score(Si,Tj)的值(若对应碱基相同,score函数得分为1分,不同则为0分),对于垂直或水平方向的元素Mi-1,j或Mi,j-1是加上k3值(若为空位则打分为-1分),递归计算相似性得分,最终取最大值为Mi,j的值。计算代价矩阵的迭代公式如下所示:
(3)
(3)回溯最佳路径。
从得分矩阵的右下角开始,一直回溯到左上角为止的路径,就是Needleman-Wunsch算法求出的序列比对最佳结果。图1所示为序列S和序列T的矩阵计算得分和回溯得到的路径图。

Figure 1 Matrix calculation score and backtracking path
从右下角最后一个单元开始回溯,矩阵单元的回溯路径方向为对角线,表示当前矩阵横轴和纵轴的2个碱基符号在同一个位置配对(包括正确匹配和错配),若路径垂直向上说明该单元纵轴方向序列碱基位置缺失,需要插入一个空位,反之,路径为水平向左表示横轴对应碱基位置插入一个空位。根据回溯路径图1所示的S和T的最佳匹配结果有2种,如图2所示。

Figure 2 Alignment results of sequence S and sequence T
3 算法优化
Needleman-Wunsch算法是目前比较典型的双序列比对算法,虽然可以得到最优的匹配结果,但是该算法也有不足之处。通过分析发现,该算法的时间复杂度和空间复杂度较高,为O(m*n),其中,m和n分别是2条序列的长度。随着日益增长的生物序列数据,高代价的时间和空间开销无疑降低了序列比对的效率[6]。
根据Needleman-Wunsch算法的实现过程可以发现,计算得分并填充矩阵的过程是导致算法时间复杂度较高的主要原因,因此本文主要针对计算得分及回溯过程进行优化。
3.1 计算得分算法的改进
在原有算法中,需要通过双层循环计算得分,根据式(3),在内层循环中需要分别计算对角线、水平和垂直3个方向的得分值分别加上各自的罚分值的总分,再对3个方向的得分进行比较获得最大值作为当前单元的得分并赋值给Mi,j。
假设2条序列分别为S={S1,S2,…,Sn}和T={T1,T2,…,Tm},当2条序列的某对应位置上的碱基相同时,即Si=Tj,在原算法的基础上,只需要将对角线值Mi-1,j-1加上匹配得分score,此时得分为最大值即可作为Mi,j的值,从而省略了对垂直和水平方向的得分计算,减少循环中的计算次数,可有效缩短计算时间。
此外,除了碱基相同时直接将对角方向值加匹配得分score作为Mi,j外,在碱基不同时,改进原算法,在内层循环中,先对3个方向的值进行大小比较,得到最大值,再加上匹配得分即为当前的Mi,j,这样可以进一步减少3个方向的计算次数。图3是改进后算法的得分计算示意图。当对应碱基相同时,Mi,j得分为Mi-1,j-1加上匹配得分k1;当对应碱基不相同时,Mi,j得分为Mi-1,j-1加上给定错配罚分k2,Mi-1,j和Mi,j-1加上空位罚分k3,最终的最大值即为Mi,j得分。

Figure 3 Calculation scheme of score matrix of improved algorithm
改进后的计算得分算法的关键代码如下所示:
for(i=1;i≤S.length();i++){
for(j=1;j≤T.length();j++){
if(S.charAt(i-1)==T.charAt(j-1)){
M[i][j].score=M[i-1][j-1].score+match;
}else{
score=max(M[i-1][j-1]),M[i-1][j],M[i][j-1]);
if(score==M[i-1][j]||score==M[i][j-1])
M[i][j].score=score+gap;
else
M[i][j].score=score+dismatch;
}
}
}
在循环开始前,对矩阵进行初始化,此时M[0][0]=0,为当前矩阵得分最大值;当进入循环结构开始执行计算得分操作时,每次循环都进行了max函数的求解,得到的均为得分结果最大值;当满足循环终止条件时,矩阵的计算得分仍为最大。因此,算法设计上满足循环不变式。
为了进一步验证算法的正确性,对原算法和改进后算法进行不同输入矩阵大小和输出比对时间的对比实验。
改进前计算得分算法输入矩阵行为950,列为1 000,执行原算法计算矩阵单元得分,运行时间为58 ms。改进后计算得分算法输入矩阵行为950,列为1 000,执行改进后的算法计算矩阵单元得分,运行时间为46 ms。
原算法计算得分的时间复杂度度为O(m*n),通过输入矩阵大小,生成对应大小字符序列,使用改进前后的算法分别对数据进行测试,发现改进后算法在时间上少于原算法,验证了改进后算法计算得分的时间效率。
3.2 回溯的改进
填充矩阵得分结束后,需要从矩阵的右下角最后一个单元开始回溯,在回溯过程中需要获取当前得分的来源,从而确定回溯路径。为了节省回溯时的判断时间,本文改进算法在原有算法的基础上,每次计算Mi,j时,只要记录上一行目标单元的后继单元。
根据图1所示的得分矩阵,首先读取M0,0单元得分并存入内存,根据打分规则,当读取M1,1得分为1且得分来源于M0,0时,将M1,1单元作为M0,0的后继节点存入。后继单元的选取采用以下规则:当出现对应同一个位置的碱基相同时(如图1中S1=T1,碱基符号均为A),此时优先获取对角线方向的单元作为后继单元;而对于可能存在的错配或有空位缺失的情况则记录各个方向。例如,图1中M1,1的后继单元包括了M1,2和M2,2,虽然M2,2是序列S和序列T在对应相同位置(即i=j)碱基的比对得分,但是在该对应位置上的碱基符号不一致,因此需要考虑M1,1的所有可能的后继单元,将M1,2和M2,2存入内存。循环执行,在计算得分的同时记录目标得分单元Mi,j,最终构建相关树形结构,通过记录有效路径的得分单元,相较于原算法可以减少回溯的次数。得分单元Mi,j的结构示意图如图4a所示,其中,Si和Tj分别表示对应位置的碱基符号,source记录Mi,j的得分来源单元,index表示当前得分单元的来源方向。index包括垂直向上、水平向左和对角线3个方向,分别以0,1,2表示,如图4b所示。
当获得相关路径的树形结构后,从最后一个节点Mm,n(m,n为序列的长度)开始回溯到起点M0,0位置,所得路径即为最佳路径。虽然前期减少了回溯的次数,但是当序列长度较大时,回溯所消耗的时间仍然较长。因此,进一步改进算法,主要是通过双向搜索的策略,从起点M0,0和终点Mm,n同时搜索,当搜索过程中出现了交点,那么该从起点到终点的路径为当前最优路径,根据节点中的index方向标记可以确定碱基之间的匹配和缺失情况,双向搜索示意图如图4c所示。改进算法在序列数据较大、节点数量较多时可以大大缩短回溯的时间,从而减少了序列比对时间,提高了整体比对效率。

Figure 4 Storage structure of target score unit and scheme of bi-directional search
改进后的双向搜索算法的关键代码如下所示:
voidbi_directionalSearch(){
while(!Queue1.empty())
Queue1.pop();
while(!Queue2.empty())
Queue2.pop();
Matrix[start.state]=1;
Matrix[end.state]=2;
Queue1.push(start);
Queue2.push(end);
While(!Queue1.empty()||
!Queue2.empty()){
if(!Queue1.empty())
directionalSearch_expand(Queue1.true);
if(found)
return;
if(!Queue2.empty())
directionalSearch_expand(Queue2.false);
if(found)
return;
}
}
改进后的算法为得分单元设计了新的数据结构,同时采用双向搜索方式减少了回溯的次数,缩短了比对时间。假设起点到终点的深度为h,每次搜索的分支因子为r,使用队列实现,每访问一个节点信息的同时将当前节点的子节点(即后继节点)依次入队。如果采用单向回溯路径,依次遍历队列中存储的节点,最大搜索的次数达到rh;若采用双向搜索策略,设置2个队列,一个用于存放从起点向终点搜索的节点信息,另一个队列用于存放从终点向起点搜索的节点信息,从起点到终点,或从终点到起点,只有h/2的深度,则最大搜索次数为2*(rh/2),理论上搜索次数明显减少。
为了测试算法理论正确性,初始化矩阵,输入起点坐标和终点坐标,通过对改进前后的算法进行数据测试,输出搜索次数。
改进前回溯算法输入起点坐标(1,1),终点坐标(10,10),执行原算法,搜索次数为10次。
改进后回溯算法输入起点坐标(1,1),终点坐标为(10,10),执行改进后算法,搜索次数为8次。
通过比较,改进后的回溯算法搜索次数小于原算法的,验证了改进后的搜索算法的有效性。
4 实验结果与分析
为了验证改进后的Needleman-Wunsch算法在双序列比对中可以有效缩短比对时间,本文设计了2次序列长度范围相同和不同的比对实验。实验中2条比对序列均从NCBI下载,其中金黄色葡萄球菌(序列大小约2.82 Mb,序列号为NC_007795.1)作为目标序列,银葡萄球菌(序列大小约为2.79 Mb,序列号为NC_016941.1)作为待比对序列。实验过程中,为了模拟序列中碱基的插入缺失,设计程序,从第1个碱基位置开始,随机生成序列长度在450~500 bp的目标序列和5条待比对序列。分别使用改进前和改进后的Needleman-Wunsch算法,依次进行5组比对实验,分别计算2条序列之间的匹配率(即序列相似性,2条序列中相同匹配碱基数量占整条序列的比例),以及序列比对时间。表2是5组比对实验的结果,其中Subject表示目标序列,Query表示待比对序列。如Staphylococcus aurers-457表示金黄色葡萄球菌序列长度为457 bp,Staphylococcus argenteus-466表示待比对的银葡萄球菌序列长度为466 bp。
从表2中可以看到,改进前后的Needleman-Wunsch算法对5组比对序列的比对时间出现了差异。在不改变序列相似性前提下,改进后的算法在比对时间消耗上普遍少于改进前的算法的。图5是改进前后Needleman-Wunsch算法关于5组长度范围相同的序列比对结果的折线图。从图5中可以更加明显地看到,改进后的算法在序列比对上所消耗的时间明显少于改进前的算法的。
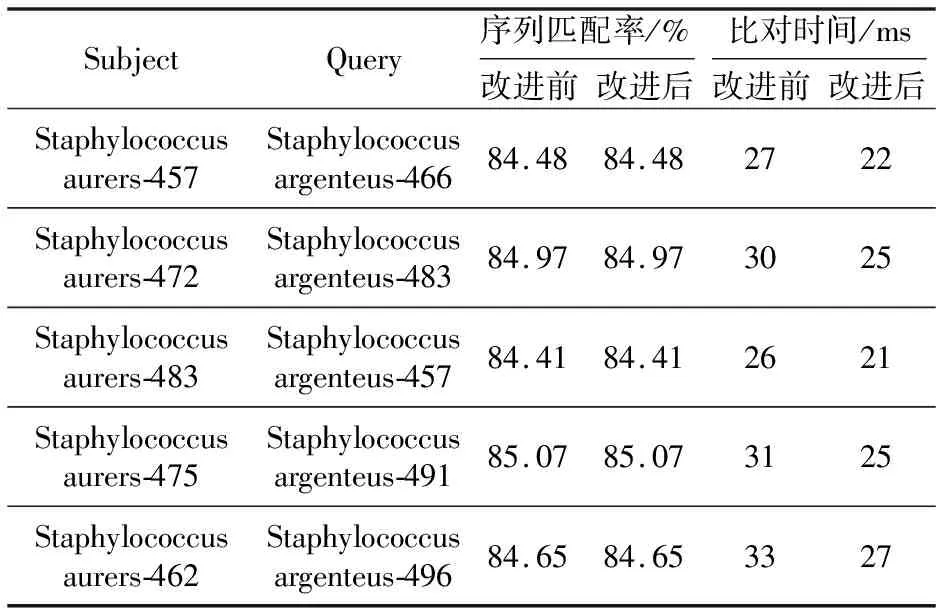
Table 2 Comparison results of 5 groups sequence alignment with the same length range for Needleman-Wunsch algorithm before and after improvement

Figure 5 Time comparison of 5 groups sequence alignment time line graphs with the same length range for Needleman-Wunsch algorithm before and after improvement
为了进一步验证改进后算法的有效性,增加了一组随机生成不同长度范围的序列的比对实验。2条比对序列同样以金黄色葡萄球菌作为目标序列,银葡萄球菌作为待比对序列。生成的5组序列长度分别为1000~2000 bp,2500~3500 bp,4500~5500 bp,6500~7500 bp,8500~9500 bp。表3所示为5组不同长度范围的序列比对结果。
从表3中可以看到,改进前后的Needleman-Wunsch算法对5组不同长度范围的序列的比对时间同样也出现了差异。改进后的算法在序列比对时间上普遍少于改进前的算法的,而改进前后的算法并不影响序列的相似性。图6是改进前后Needleman-Wunsch算法关于5组长度范围不同的序列比对结果的折线图。从图6中可以更加明显地看到,改进后的算法在运行时间上少于原算法的。
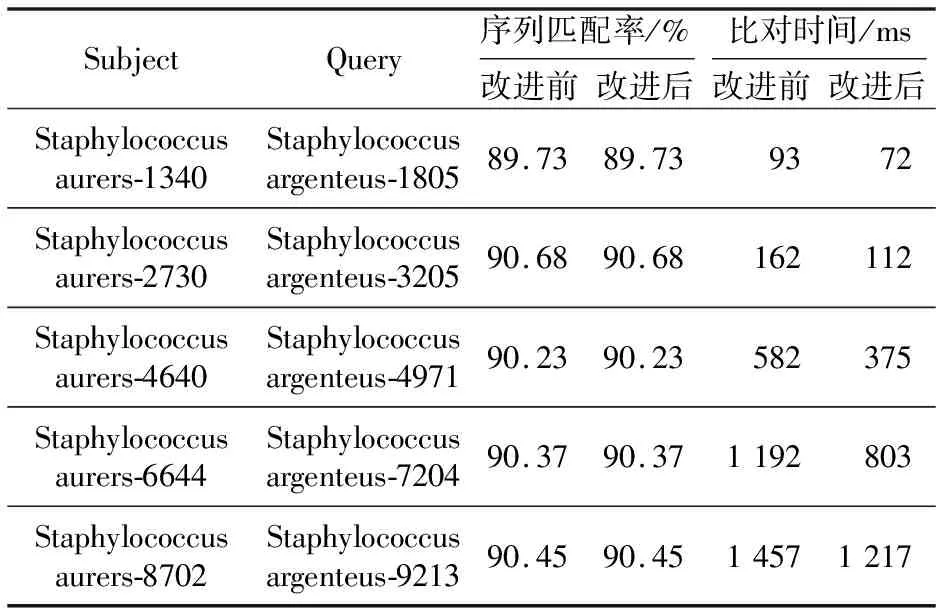
Table 3 Comparison results of 5 groups sequence alignment with the different length range for Needleman-Wunsch algorithm before and after improvement

Figure 6 Time comparison of 5 groups sequence alignment time line graphs with the different length range for Needleman-Wunsch algorithm before and after improvement
通过以上2组实验可以验证改进后的Needleman-Wunsch算法有效地缩短了序列比对时间。为了进一步验证改进后的算法在缩短实际生物全基因组序列的比对时间上同样有效,采用2019年新型冠状病毒和2003年的SARS病毒序列进行比对实验。新型冠状病毒信息从国家生物信息中心(NGDC)下载,SARS病毒信息从NCBI下载,将文本形式的2条基因序列读入程序中并进行测试。实验中,对2种不同病毒的核酸序列同样进行了5次比对测试,最终获得序列比对的平均相似性和平均比对执行时间。表4是改进前后Needleman-Wunsch算法关于新型冠状病毒和SARS病毒全序列的比对相似性和比对运行时间。其中2019-nCov表示新型冠状病毒,序列总长度为29.9 kb,SARS-Cov表示SARS病毒,序列长度为29.7 kb。
从表4中可以看到,改进后的Needleman-Wunsch算法相较于原算法,在全局序列比对下得到的序列相似性为78.6%,与实际公布的序列比对结果相近,说明该算法计算生物序列的相似性是可靠的。实验中,改进后算法在序列比对时间上少于改进前算法的时间,因此,改进后的Needleman-Wunsch算法在不影响序列相似性的前提下,可以有效地缩短序列比对时间,提高比对效率。

Table 4 Results of novel coronavirus and SARS virus sequence alignment for Needleman-Wunsch algorithm before and after improvement
5 结束语
序列比对是生物信息研究中最基础、最重要的研究。通过序列比对可以获取不同生物之间序列的相似性程度,揭示基因序列之间的同源性,探索发现生物序列中的功能、结构和进化信息[7]。
基于动态规划的Needleman-Wunsch双序列比对算法虽然可以获得序列的最优比对结果,但是时间开销和空间开销都较大。伴随着海量生物数据的增长,对序列比对的运行时间的要求也越来越严格。本文改进了Needleman-Wunsch计算得分算法及回溯策略,结合实验验证了算法的有效性。结果表明,改进后的算法在一定程度上缩短了序列比对的时间,提高了比对效率。但是,在序列数据较大的情况下,该算法的空间复杂度较大,且序列比对效率仍然有待提高,在后续的研究中将继续探讨该算法的改进问题,以进一步提高程序运行效率,缩短序列比对运行时间,降低空间复杂度[8]。

