圆柱定子直线超声波电机定子机电耦合模型研究*
陈 强,蒋春容
(南京工程学院电力工程学院,南京 211167)
0 引言
与传统电磁电机相比,超声波电机具有结构简单、定位精度高、低速大推力、无减速齿轮直驱负载、噪声小、摩擦式自锁等优点[1-2]。直线超声波电机除了超声波电机的共同特点外,还具有无需丝杆机构转换直接输出直线运动推力的特性[3-4]。建立数学模型精确地反映超声波电机的运行特性,对于指导电机的结构优化、新型样机制作和控制具有重要的意义。目前,超声波电机的模型研究主要是等效电路模型法[5-6]和理论分析法[7-8]。等效电路模型为近似等效模型,主要为超声波电机的驱动控制提供模型基础,电机设计和结构优化方面不具优势。理论分析法主要是有限元法和动力学模型,有限元法运算量太大需要较长的时间进行运算,动力学模型可通过数学模型直接得到电机的输入输出特性。
本文利用Hamilton能量变分原理对一款大推力圆柱定子直线超声波电机定子进行建模,推导出电机定子的机电能量系统。通过对能量的变分,导出电机定子的运动方程,建立圆柱定子超声波电机的定子机电能量转换模型,对已建立的理论模型进行仿真,并对样机进行实验分析。
1 圆柱定子直线超声波电机机理
圆柱定子结构如图1所示。采用兰杰文振子,八阶弯曲振动和三阶纵向振动复合的振动模态,定子上安装两驱动足交替驱动动子作直线运动。对纵向振动和弯曲振动陶瓷片施加频率相同、相位差90°的激励电源,产生相位差为90°的两种振动模态,使定子驱动足接触面质点产生椭圆运动,从而推动动子滑行。压电陶瓷片分四组,每组两片,从每组陶瓷片中间引出电极接激励电源,陶瓷片与定子匹配块接触面接地。纵振压电陶瓷片为纵向极化,反向极化叠在一起;每片弯振压电陶瓷均分成两部分,且极化方向相反。

(a) 定子结构图

(b) 压电陶瓷片的结构和极化方向图1 定子结构
图2为定子振型,V为纵向振动速度,Vb为弯曲振动速度,T为纵振产生的纵向压力,电机定子固定预紧点位于两种振动模态的共同节面处。

图2 定子振型
2 定子的Hamilton方程
压电振子是微小振动,可线性叠加,由Hamilton能量变分原理可得圆柱定子纵振和弯振的变分方程[9-10]:

(1)

(2)
式中,Lz=Tz-Uz+Ez,Lw=Tw-Uw+Ew,Tz、Uz和Ez分别为定子纵振下的动能、势能和压电陶瓷电场能,Tw、Uw和Ew分别为定子弯振下的动能、势能和压电陶瓷电场能,δWez为纵振下外部施加的电能,δWew为弯振下外部施加的电能。
3 定子纵振模态下建模
纵向振动,应变应力矢量矩阵可以缩减为:
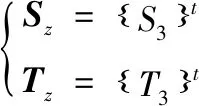
(3)
金属弹性体的劲度常数矩阵缩减为3×3的矩阵[12]:
cs z= {cs33}
(4)
式中,cs33=EYs/(1-μs2),EYs为金属弹性体的弹性模量,μs为金属弹性体的泊松比。
纵向激励电压在压电陶瓷上产生的电场强度为:
Ez=Nφz(z)·Vz/tp=Nez·Vz
(5)
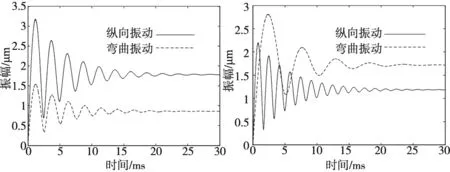
式中,Vz={Vzmaxsinωt},Vzmax为纵向激励电压幅值;Nφz(z)为纵向电势的形函数矩阵,只与电极z方向的值有关。根据图1中的电极设置,电势的形函数矩阵的分量:Nφz(z)=1,其中l2-2 定子纵振瞬时幅值矢量为: U1=Nz·U1z (6) 式中,Nz={cos(3πz/l)},U1z={ξBcos(ωt+π/2)}t,ξB为纵振幅值。电机定子纵振下的动能为: (7) 定子势能由金属弹性体和压电陶瓷两部分组成,定子纵振模态下势能为: (8) 式中,Sz和Tz为纵振下应变矢量和应力矢量,Sz=Nzs·U1z,Nzs=∂Nz/∂z。由第二类压电方程,可得: (9) 纵振压电陶瓷的电场能: (10) 纵向激励外部施加电能的变分: (11) 式中,qz为纵向激励施加在电极上的电荷矢量。 Vz仅对纵振压电陶瓷片作用,超声波电机定子的纵振能量为: (12) 电机定子纵振能量的变分为: (13) 将式(11)和式(13)代入将式(1),根据δU1zt与δVz为两个相互独立的变分,得到电机定子纵振仿真模型为: (14) 实际电机定子振动系统会有阻尼存在,对式(14)添加阻尼项Cz,得到电机定子纵振的振动方程: (15) 弯振可忽略振动引起的纵向变形,振动后定子横截面仍为圆形,如图3所示,θ为横截面变形前后夹角: (16) 式中,ξA为弯振幅值,α→0,tanα≈α,可得: α=sin(9πz/l)(9πξA)/(2l) (17) 图3 定子弯曲振动示意图 由于圆柱定子轴对称性和定子横截面保持为圆形,弯振应变应力矢量矩阵可以缩减为: (18) (19) 式中,U2={u,v}t,u、v分别为定子各点在x、z方向的位移。弯曲激励电压在压电陶瓷上电势为: φw=Nφw(z)·Vw (20) 式中,Vw={Vwmaxsinωt},Vwmax为激励电压幅值;Nφw(z)为弯振电势的形函数矩阵。根据图1中的电极的设置,电势的形函数矩阵的分量为: (21) 弯振激励电压在压电陶瓷上产生的电场强度为: Ew=New·Vw (22) 式中,New=Nφw(z)/tp。 定子各点在x、z方向的位移分别为: u(x,z)=-ξAcosωtcos(9πz/l)+x·sinθcosωt≈ -ξAcos(9πz/l)·cosωt (23) v(x,z)=xcosθcosωt≈9πξAxsin(9πz/l)cosωt/l (24) 则可得: U2=Nw·U2w (25) 将式(25)代入式(19)得: Sw=Nws·U2w (26) 电机定子弯振下的动能: (27) 定子势能由金属弹性体和压电陶瓷两部分组成,定子弯振模态下势能为: (28) 弯振压电陶瓷的电场能为: (29) 外部施加电能的变分: (30) 式中,qw为弯曲激励施加在电极上的电荷矢量。 Vw仅对弯曲振动压电陶瓷片作用,超声波电机定子的弯振能量为: (31) 参照纵振仿真模型求取,弯振仿真模型为: (32) 对式(32)添加阻尼项Cw,得到电机定子的弯振振动方程: (33) (34) 阻尼系数为: c1=ηc0 (35) 式中,η为阻尼比。本文所研究电机,纵振阻尼比为η0, 弯振阻尼比为η1。 利用Matlab/Simulink建模仿真,并进行实验分析。电机结构参数:定子长度l为282 mm,定子中间匹配块横截面外半径R1为10 mm,定子中间匹配块横截面内半径R2为3.25 mm,压电陶瓷的厚度tp为2 mm,压电陶瓷横截面外半径r1为10 mm,压电陶瓷横截面内半径r2为4 mm,l1为129 mm,l2为137 mm,定子金属弹性体材料的密度ρs为2780 kg/m3,定子金属弹性体材料的杨氏模量EYS为7.3×1010N/m2,定子金属弹性体材料的泊松比μs为0.31,压电陶瓷材料的密度ρp为7500 kg/m3,阻尼比η0和η1均为0.2%。 施加电压值为400 V,振幅随频率变化如图4所示, 图4a为纵向振动振幅随频率变化曲线,图4b为弯曲振动振幅随频率变化曲线。当激励电压频率为谐振频率时振幅最大,越接近谐振频率点振幅越大。从图中可知29.8 kHz最接近纵向振动谐振频率,30.6 kHz最接近弯曲振动谐振频率。 (a) 纵向振动 (b) 弯曲振动图4 定子振幅和频率关系 起动过程中,电机定子振幅变化曲线如图5所示,激励电压幅值为400 V。当加上激励电压之后,电机定子的振幅需要从0升至稳定值。电机定子并不是瞬间达到工作的最大值,而是在起动过程中,电机定子的振幅从零振荡升至稳定值,当激励电压频率越接近谐振频率则振荡越小,激励电压频率等于谐振频率时起动过程没有振荡。 (a) 激励电压频率为29.8 kHz (b) 激励电压频率为30 kHz (c) 激励电压频率为30.2 kHz (d) 激励电压频率为30.4 kHz (e) 激励电压频率为30.6 kHz图5 起动过程中电机定子振动振幅 图6为实验样机,图7为样机驱动电压和动子速度曲线,定子预压力为30 N,驱动电压频率为25.2 kHz,驱动电压和动子速度成正比,工作频率误差主要是电机加工导致[3]。由图7可见,驱动电压和动子速度近似成正比,驱动电压越大,动子速度越大,这主要是由于驱动电压增大时,定子的振幅随之增大,从而使定子对动子的驱动速度变大导致的。 图6 实验样机 图7 电机速度-驱动电压曲线 本文利用Hamilton能量变分原理建立了圆柱定子直线超声波电机定子的机电能量转换模型,并利用Matlab/Simulink对机电能量转换模型进行了求解,对定子的振动性能进行了仿真分析。分析结果表明:当激励电压频率为谐振频率时振幅最大,越接近谐振频率点振幅越大;在起动过程中,电机定子的振幅从零振荡升至稳定值,当激励电压频率越接近谐振频率则振荡越小,激励电压频率等于谐振频率时起动过程没有振荡。制作了样机,对样机进行了实验验证,结果表明 驱动电压和动子速度近似成正比。本文建立的机电能量转换模型较为精确地给出了电机定子的机电耦合特性,对电机设计以及电机控制有一定的指导意义。3.1 定子纵振模态下动能
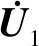
3.2 定子纵振模态下势能
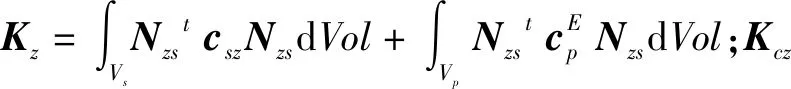
3.3 纵振压电振子电场能
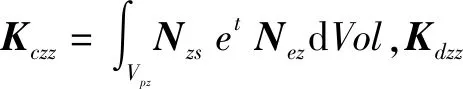
3.4 纵向激励外部施加的电能
3.5 纵振仿真模型
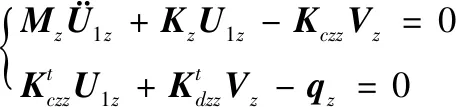
4 定子弯振模态下建模

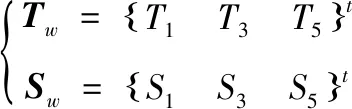

4.1 定子弯振模态下动能



4.2 定子弯振模态下势能

4.3 弯振压电振子电场能

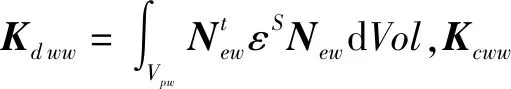
4.4 弯曲激励外部施加的电能
4.5 弯振仿真模型

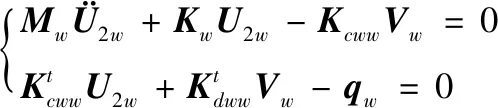

5 仿真与实验分析




6 结论

