基于NMPC的仿人攀爬机器人运动优化*

马 斌

(重庆工商大学机械工程学院，重庆 400067)

0 引言

机器人不仅在工业领域得到了广泛的认可，而且在人类生活领域也发挥着重要作用。人形机器人的形状类似人类，因此它们对人类较为友好，可以使用为人类设计的系统。这是人形机器人被期望积极参与人类生活空间的原因之一[1]。为了在这样的生活空间中成功地工作，人形机器人必须能够表现得与人类相似。由于这个原因，人形机器人的行走和奔跑运动已经得到了深入的研究[2]。攀爬运动的控制方法也可以潜在地应用于崎岖地形环境下的运动。

攀爬墙体是通过在肢体和地形特征之间产生接触力来完成的，例如突出物、洞和裂缝，这些统称为“支撑物”。以往的方法需要两个步骤才能完成爬升运动[3]。在第一步中，确定仿人机器人的可能路径。在第二步中，确定肢体跟踪路径所需的运动。Almonacid M等提出的路径规划方法[4]，首先探索每个肢体适用的支撑物组合，然后寻找从开始到目标的一系列可行的支撑物组合。接着在考虑机械约束的同时，生成肢体轨迹以遵循上一步中找到的路径。换言之，传统的控制方法一步一步地分别产生路径和运动。因此，不能实现攀爬运动的整体优化以最大化攀爬效率。

为解决这一问题，本文提出了一种控制方法，能够同时优化攀爬路径和运动，使攀爬运动变得更加流畅、实时性更高。将仿人机器人的攀爬任务视为一个考虑机械约束的NMPC问题[5]，并使用基于墙体图的状态相关权重和势函数。在现有方法中，当墙体的信息发生变化(例如检测到新的支撑物)时，机器人必须停止爬升并生成新的路径[6]。相比之下，在提出的方法中，如果计算速度足够高，则可以实时处理墙体信息的变化。但是，使用具有多个支撑的复杂墙体模型来计算控制输入需要花费大量的时间。因此，为了减少计算成本，还提出了一种视距评估方法，以便从所有可用的信息中选择必要的信息。

1 系统建模

1.1 仿人机器人模型

图1 十自由度连杆 仿人机器人模型

研究采用了一个在垂直平面上具有10个自由度和10个连杆的机器人模型，如图1所示。假设机器人仅在垂直平面上移动得足够慢。因此，只考虑运动学模型而不考虑动力学模型。每个连杆的端坐标用Qi=(Qi,x，Qi,y)表示。并且机器人的右手、左手、右脚和左脚的端点坐标分别表示为q1、q2、q3和q4=(Q3、Q5、Q8和Q10)。正方向定义为逆时针方向[7]。相对角度矢量φ定义为：

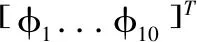
(1)

式中，φi为与根连杆的相对角度。但是，φ1和φ2是从水平轴到Q0的相对角度。将连杆i的坐标系到绝对坐标系的齐次变换矩阵定义为Ti(φ,Q0)。

(2)

式中，Q0为连接杆件1和6的关节坐标，且被定义为机器人的中心；Qi为每个连杆的端点坐标；φ为相对姿态角；li为连杆i的长度；mi为连杆i的重量。机器人中心和每个肢体末端的垂直速度表示为：

(3)

机器人在保持平衡的同时，通过每个关节和手动致动器在支撑物上产生支撑力和扭矩来攀爬力和扭矩的平衡方程[8]表示如下:

(4)

(5)

(6)

式中，g为重力加速度；Qg,i为每个连杆的质心坐标，。fi,x为每个肢体qi(i=1,...,4)端点在水平方向上的支撑力；fi,y为每个肢体qi(i=1,...,4)端点在垂直方向上的支撑力；τi为每个肢体qi(i=1,...,4)的端点产生的扭矩。

1.2 墙体模型

假设墙体是垂直平面，并将其设置为xy平面。y轴正方向被视为垂直正方向。假设当每条肢体的端点处于保持状态(支撑物上)时，机器人可以产生夹持力。墙体上每个点(x,y)在y轴方向上可以产生的最大夹持力表示为：

(7)

式中，fpi,y为在支撑i处沿y轴方向可以产生的最大夹持力，其坐标点是(xi,yi)。我们称这个函数为最大夹持力函数。图2给出了该函数的一个示例。类似地，在支撑i处x轴方向的最大夹持力和最大扭矩分别由fpi,x和τpi表示。还考虑了最大持力函数Fmax,x(x,y)和Tmax(x,y)。

图2 最大夹持力函数

2 提出的控制方法

2.1 非线性模型预测控制

本文采用实时最优控制中的NMPC来处理非线性的、有约束的控制问题。Kayode owa等[5]对NMPC的多种应用案例有详细的解释说明。Yu M等[9]已经考虑了将攀爬任务定义为NMPC的基本思想，但是其设置非常简单。而在本文将对基于NMPC的仿人攀爬机器人运动进行更加详细的分析。

在NMPC中，非线性系统的状态描述方程为：

(8)

式中，x(t)为状态向量，u(t)为输入向量，p(t)为给定时变参数。考虑从当前时间t到有限未来时间t+T的性能指标J。NMPC中最优控制输入为uopt(t)(t≤τ≤t+T)，同时考虑如下约束条件：

C(x(τ),u(τ),p(τ))=0

(9)

可见最优控制输入uopt(τ)取决于当前时间t和状态x(t)，因此，它可以表示为uopt(τ;t,x(t))。将最优控制输入的初始值用作时间t处的实际控制输入。

u(t)=uopt(t;t,x(t))

(10)

这样，在每个采样时间，通过求解直到有限未来的最优控制问题来计算控制输入。采用Continuation/GMRES算法作为实时数值优化方法实现求解线性方程组。对于NMPC来说，只要计算成本不是太高，任何求解大规模非对称稀疏线性方程组的最常用方法都可以应用到该问题中。

2.2 控制模型

为了让人形机器人使用NMPC实现攀爬运动，设状态x为：

(11)

且设输入u为：

(12)

式中，f为夹持力；d为伪输入集合，由伪输入di(i=1,...,12)组成。

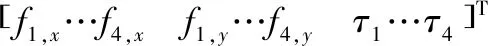
(13)

然后，状态方程表示为：

(14)

由每个肢体qi端点产生的夹持力fi,x、fi,y和扭矩τi的约束条件为：

-fmaxi,x≤fi,x≤fmaxi,x

(15)

-fmaxi,y≤fi,y≤fmaxi,y

(16)

-τmaxi≤τi≤τmaxi

(17)

其中，

fmaxi,x=Fmax,x(qi)

(18)

fmaxi,y=Fmax,y(qi)

(19)

τmaxi=Tmax(qi)

(20)

可以使用伪输入di将上述方程转换为如下情况：

(21)

(22)

(23)

上述3个方程和方程(4)～方程(6)是NMPC中的约束条件。

2.3 路径和运动的综合优化方法

(1)性能指标：攀爬性能指标J表示如下：

(24)

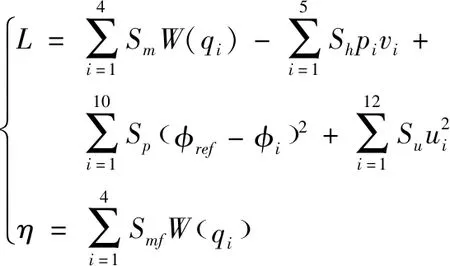
(25)

式中，Sm,Sh,Sp,Su,Sd,Smf为权重；W为势函数；pi为变权重；φref为参考姿态角。L(x(τ),u(τ))和η(x(t+T))的第一项通过势函数W引导机器人的肢体攀爬，这将在本节后面解释。L(x(τ),u(τ))L(x(τ),u(τ))的第二项中变权重pi定义为:

(26)

式中，vref为目标爬升速度。pi代表了每个肢体的实际位置和目标位置之间的差异。例如，如果肢体长时间停留在一个保持状态，pi值会增加，因此该肢体会被引导到y轴正方向。L中第一项和第二项之间的大小变化，会导致在夹住一个支撑和释放另一个支撑之间的切换，并提示应该选择哪些肢体释放它们的支撑。L的第三项稳定机器人的姿势，第四项使输入变小。L的第五项确保伪输入是正的[10]。通过引入这一项，可以唯一地确定满足约束条件(式(21)～式(23))的解(fi,di)。

(2)最大夹持力函数：公式(7)中定义的函数Fmax,x(x,y)、Fmax,y(x,y)和Tmax(x,y)是不连续的。NMPC数值优化中不连续函数的处理比较困难，因此将最大持力函数近似化为以下提出的连续函数：

(27)

(28)

(29)

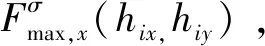
为了满足上述两个目标，引入了两个新参数：σJ和σC。在每个肢体产生的夹持力最大值fmaxi,x,fmaxi,y、扭矩最大值τmaxi以及势函数W表示如下：

(30)

(31)

(32)

(33)

(3)视距评估：如果墙体上有许多支撑，则最大持力函数(式(27)～式(29))会导致相当高的计算成本。这是因为随着支撑数量的增加，最大保持力函数变得复杂。为了避免这个问题，引入了视距评估。

假设NMPC的时域长度小于从当前时间到机器人完成攀登的时间长度。在这种情况下，运动只能预测和优化到特定的未来时间。因此，即使使用所有的墙体信息来优化运动，其中一些信息也不会影响最优解。此外，由于NMPC本身是一种计算量大的控制方法，因此很难将视界长度延长到机器人完成攀爬的时间。注意到，即使在有限的信息范围内，也可以根据所有的墙体信息计算出控制输入。这个范围被定义为“视距”范围。除了时域长度外，它还取决于模型的状态或参数。在本研究中，以机器人的中心坐标Q0、速度v和相对姿态角φ作为确定视距评估的参数。这样，通过减少需要评估的信息量来减少计算时间。

为了将支撑限制在视距范围内，将式(28)～式(29)中的最大夹持力函数替换为：

(34)

(35)

(36)

式中，I为由视距范围内的支撑组成的评估集。从定义来看，I⊂H。让视距范围成为以机器人Q0为中心的圆形范围。评估半径由该圆的半径表示。两种墙体模型如图3所示。左边的例子是式(27)～式(29)中最大夹持力函数的一个示例，它用连续函数来近似。右边的是式(34)～式(36)中最大保持力函数的一个示例，它仅限于视距范围。

(a) 具有连续函数的墙体模型 (b) 具有视距范围的墙体模型图3 墙体模型

随着函数的变化，在每个肢体产生的夹持力最大值fmaxi,x,fmaxi,y、扭矩最大值τmaxi以及势函数W替换如下：

(37)

(38)

(39)

(40)

3 实验及结果分析

3.1 仿真设置

利用计算机数学软件Maple，在Visual Studio 14.0编译环境中使用C语言对提出的控制方法进行了机器人行为模拟。

表1列出了与机器人相关的参数。这些参数都是无量纲的。机器人在仿真开始时的初始姿态如表2所示，此时机器人是静止的，机器人的中心坐标Q0位于原点(0,0)。假设此姿势为稳定姿势，则性能指标中参考姿势角φref的值将设置为与初始姿势角度相同的值。与墙体相关的参数如表3所示，与性能指标相关的参数(例如权重)如表4所示。

表1 机器人参数

表2 初始姿势参数

表3 墙体参数

表4 性能指标参数

初始姿态和支撑布置情况如图4中Time0所示。仿真的计算条件如表5所示，参考了文献[10]的设置经验。

图4 攀爬行为结果(Case 4)

表5 仿真的计算条件

3.2 仿真结果

从图4可以看出，机器人能够根据墙体信息实现支撑选择和爬墙支撑切换，验证了提出控制方法的可行性。Case 1、Case 2、Case 3和Case 4更新一次控制输入的计算时间分别为12.4、15.2、18.5和19.5 ms。这些结果表明，随着评估半径的减小，计算时间也随之减少。这是因为用于仿真的墙体信息量随着评估半径的减少而减少。

3.3 真实案例测试

选择近藤公司的KHR-3HV型仿人机器人对提出控制方法进行了实际攀爬测试。该仿人机器人没有特殊的抓握机构，而是采用角托架作为手，符合本文模型设定。此外，设计了一个攀爬的简易墙体，由多孔木墙制成。支撑物是由金属环制成的。同仿真实验一致，也使用了不同的评估半径来执行仿人攀爬机器人行为控制。同仿真一样，图5给出了Case 4的实际行为结果。每个Case均执行10次并取平均获得攀爬全过程的时间。结果显示，Case 1、Case 2、Case 3和Case 4的时间排序与仿真结果一致。相比于Case 4(154 s)，Case 1(97.9 s)的攀爬时间减少了36.4%，验证了提出控制方法的有效性。

图5 实测攀爬行为结果

4 结论

本文提出了一种基于NMPC的仿人机器人攀爬控制方法。该方法能够在考虑机械约束的情况下实现路径和运动的综合优化，并通过使用视距评估在线配置性能指标来减少计算时间。与将墙体上的所有支撑都纳入视距范围的情况相比，攀爬时间减少了36.4%。使用状态相关权重的性能指标不仅可以应用于机器人的攀爬控制，还可以应用于其他NMPC问题。此外，该视距评估方法还可以应用于具有复杂环境下的机器人或者车辆控制问题。但是，真实实验中每种Case的计算时间都略长于控制输入的更新周期。后续将考虑使用高性能的计算机或开发一种新的方法来更有效地确定评估范围以便解决这个问题。