黏滞阻尼器位移损失对结构减震性能的影响研究

冉田苒， 石 诚， 张同亿， 张娜彬， 黄 明

(中国中元国际工程有限公司， 北京 100089)

0 引言

在实际工程设计中，由于阻尼器与主体结构连接的支撑刚度是有限的(量级在105kN/m)，阻尼器位移在刚度上的损失(简称刚度位移损失)不可避免。而阻尼器的位移损失直接影响减震效果。因此，有必要研究位移损失在不同结构类型中、不同地震作用下对减震效果的影响规律，进而寻求如何使减震结构在不同地震作用下达到最优减震率。这对减震结构设计的优化具有重要意义。

关于支撑刚度对消能减震结构减震效果的影响，已有学者对其进行过研究。欧进萍等[1]指出，当结构振动频率和耗能器黏滞阻尼系数一定时，存在最佳的支撑刚度，使得减震效果达到最佳。蒋通等[2]指出，支撑与非线性阻尼器的串联刚度越大，消能结构位移和剪力的减震效果越好。

虽然业界普遍得出了可以通过调整支撑刚度来提高减震效果的结论，但是，对于不同地震作用、不同阻尼系数、不同结构类型下，应用黏滞阻尼器的消能减震结构的减震效果变化规律和支撑刚度、位移损失之间的关系，尚缺少深入的论证与总结[3-9]。

本文从黏滞阻尼器减震结构的附加阻尼比公式出发，引入位移损失，进行了基于单自由度体系的理论推导和基于实际工程的模型实例验证。

1 理论推导

带黏滞阻尼器结构的单自由度基本体系(简称基本体系)如图1所示(ks为主体结构刚度；C为阻尼器的阻尼系数；α为阻尼器的阻尼指数)，因为主要研究对象为阻尼器的附加阻尼，故设定原结构无模态阻尼。

(1)

式中：kb为支撑刚度；kd为阻尼器Maxwell模型串联刚度；ke为等效串联刚度(kd与kb串联的刚度)。

图1 黏滞阻尼器减震结构的基本体系

根据《建筑消能减震技术规程》(JGJ 297—2013)[10]中附加阻尼比ζ的计算公式，可以得到基本体系中附加阻尼比ζ的计算公式为：

(2)

式中：λ为阻尼指数的函数；F为阻尼器的最大阻尼力；d为阻尼器最大位移，按式(3)计算；Fs为结构的最大楼层剪力；ds为结构的最大楼层位移。

d=ds-d损

(3)

式中d损为阻尼器的有效位移损失，其由刚度位移损失和变形模式损失两部分组成，由此可假定：

(4)

式中：μ为损失系数，由于阻尼器出力在时程过程中是不断变化的，因此引入系数μ对最大阻尼力进行修正；ηd为变形模式损失率，即由于“弯曲型”变形造成的位移损失率。

将式(3)，(4)代入式(2),可得：

(5)

因为有：

Fs=ksds

(6)

将式(6)代入式(5)，可得：

(7)

设：

(8)

将式(8)代入式(7)，可得：

(9)

可见，附加阻尼比ζ是变量x的一元二次方程，且开口向下。因此，ζ存在最大值。当ζ取最大值时，有：

(10)

将式(8)代入式(10)，变换形式写为：

(11)

式中xop为令附加阻尼比ζ取得最大值的x值。

令：

(12)

(13)

式中：d损ke为最大刚度位移损失，即对应于最大阻尼力的等效串联刚度上的位移损失；ηke为刚度位移损失率，即对应于最大阻尼力的等效串联刚度上的位移损失与结构最大层间变形之比。

将式(13)代入式(7)有：

(14)

当ζ取最大值时，有：

(15)

式中ηke-op为最优损失率，即令附加阻尼比ζ取得最大值的刚度位移损失率。

由式(15)可知，最优损失率ηke-op只与变形模式损失率ηd和损失系数μ有关。ηd，μ的取值范围应在0和1之间,ηd的取值与结构类型有关，μ的取值与结构地震响应有关。关于ηd，μ的具体取值问题将另行研究，在此不做深入探讨。

将式(15)代入式(14)，可得最优附加阻尼比为：

(16)

由式(15)可知，当阻尼指数一定时，最优附加阻尼比ζmax与等效串联刚度和结构刚度的比值(简称损失刚度比，定义为y=ke/ks)和变形模式损失率ηd有关。y越大，ηd越小，则ζmax越大。

假定阻尼指数不变(α=0.2)，附加阻尼比随刚度位移损失率ηke变化的曲线如图2～ 4所示，分别研究了损失刚度比y、变形模式损失率ηd、损失系数μ对附加阻尼比随ηke变化规律的影响。

由图2～4可以看出：1)随损失刚度比y增大，最优损失率ηke-op不变，最优附加阻尼比ζmax增大；2)变形模式损失率ηd越大，则ηke-op越小，ζmax越小；3)损失修正系数μ越大，则ηke-op越小，ζmax越小。

2 实际工程模型

本文采用的模型来自新疆某医院工程，采用ETABS软件建模[11]。框架结构模型和框剪结构模型概况如表1和图5、图6所示。抗震设防烈度为8度(0.2g)，场地特征周期为0.45s。阻尼器支撑采用人字撑形(简称人字撑)布置与墙式布置(图7，8)。人字撑截面为□300×300×12，侧向刚度为2.95×105kN/m；支撑墙截面厚度为300mm，宽度4 100mm，剪跨比小于1。

图2 损失刚度比y对ζ-ηke曲线变化规律的影响(ηd=0，μ=1)

图3 变形模式损失率ηd对ζ-ηke曲线变化规律的影响(y=1, μ=1)

图4 损失系数μ对ζ-ηke曲线变化规律的影响(y=1, ηd=0)

图5 框架结构模型

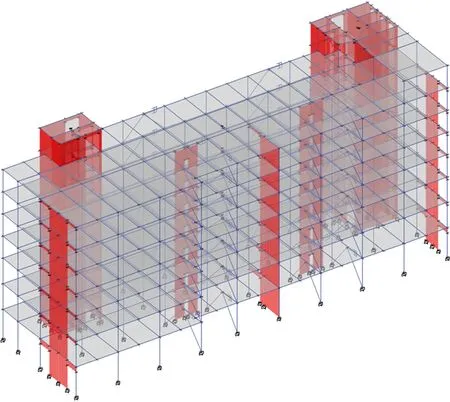
图6 框剪结构模型

图7 框架结构模型阻尼器布置

模型概况 表1

图8 框剪结构模型阻尼器布置

算例的地震激励采用两条天然波(天然波1、天然波2)和一条人工波，其多遇地震反应谱如图9所示。分别计算不同地震作用、不同阻尼系数下减震结构的最大层间位移角减震率θ(简称减震率θ，框架结构基于第2层，框剪结构基于第5层)，并用1节理论推导的结论对其进行分析。减震率θ的定义如下：

(17)

式中：d有控为有控结构的层间位移角；d无控为无控结构的层间位移角。

图9 地震波反应谱

3 计算结果

固定阻尼指数α不变(α=0.3)时，分别计算框架结构、框剪结构在小震、中震、大震作用下X向减震率θ随阻尼系数C的变化。计算结果如图10，11所示。

由图10，11可以看出，随阻尼系数C的增加，减震率θ呈现先增大后减小的规律。小震、中震、大震作用下，最优减震率θmax对应的阻尼系数C逐渐增加，但θmax基本保持不变。框剪结构的θmax明显小于框架结构的θmax。

减震率θ随地震作用的变化趋势和阻尼系数C有关。当阻尼系数C较小时，减震率θ随地震作用的增大而减小(小震下减震率θ最大)；随阻尼系数C的增加，其规律逐渐过渡到减震率θ随地震作用的增大先增后减(中震下减震率θ最大)，直至减震率θ随地震作用的增大逐渐增大(大震下减震率θ最大)。

图11 框剪结构模型减震率θ随阻尼系数C的变化规律

可以看出，在进行减震结构设计时，若仅追求小震作用下减震率θ最大，则中震、大震作用下的减震率θ将递减，可能造成减震结构在中震、大震作用下的安全储备减少。因此，应综合小震、中震、大震的减震效果进行设计。如将小震、中震的减震率θ调节至近似，此时虽然小震作用下的减震效果不是最优，但中震、大震作用下的减震效果增强，提高了结构在中震、大震作用下的安全储备。

4 计算结果分析

在单自由度体系的理论推导中，主要依靠附加阻尼比ζ来评价减震效果，而附加阻尼比ζ和减震率θ为正相关。因此，可以用附加阻尼比ζ的变化规律对减震率θ的变化规律进行分析。

4.1 阻尼系数对减震率的影响分析

当地震作用不变时，随阻尼系数C增加，阻尼器出力F显著增大，而结构位移响应ds的变化相对而言并不显著。因此，由式(13)可知，刚度位移损失率ηke随阻尼系数C增大而增大，逐渐接近最优减震率ηke-op，直至越过ηke-op。因此减震率θ随阻尼系数C增大呈现先增大后减小的趋势。

当地震作用增加时，由于结构位移响应ds增加，需要更大的阻尼器出力F才能使ηke达到ηke-op，故小震、中震、大震作用下最优减震率θmax对应的C逐渐增大。

由式(16)可知，最优阻尼比ζmax与地震作用无关。实际工程算例中，小震、中震、大震作用下的最优减震率θmax基本不变，与式(16)相契合。

同样由式(16)可知，损失刚度比y越小、变形模式损失率ηd越大，则最优阻尼比ζmax越小。这解释了算例计算结果中框剪结构的最优减震率θmax相对框架结构较小(框架结构θmax为50%左右，而框剪结构θmax为30%左右)的原因，即：框剪结构相对框架结构的y较小，ηd较大。本例中，框剪结构的各层平均损失刚度比y为0.37，而框架结构的各层平均损失刚度比y为1.64。

图12 C较小时，地震作用变化对应的损失率及附加阻尼比变化

图13 C适中时，地震作用变化对应的损失率及附加阻尼比变化

图14 C较大时，地震作用变化对应的损失率及附加阻尼比变化

4.2 地震作用对减震率的影响分析

根据式(13)，对于黏滞阻尼器的刚度位移损失率，有：

(18)

式中:w为结构的振动响应圆频率;v为阻尼器的速度;d为阻尼器的位移。

随地震作用的增加，结构位移响应ds增加，但对于非线性黏滞阻尼器(0<α<1)，阻尼器出力F随ds的增加并不明显。因此，由式(18)可知，随ds增加，非线性黏滞阻尼器的刚度位移损失率ηke将减小。

以上述框架结构模型为例，用支撑的总侧向刚度除以结构层侧移刚度的平均值，可以得到其各层平均损失刚度比y=1.64。假定损失系数μ=0.7，变形模式损失率ηd=0.3，可以根据式(14)画出对应的单自由度体系的附加阻尼比ζ随刚度位移损失率ηke变化的曲线，如图12～14所示。

由4.1节中的论述可知，刚度位移损失率ηke与阻尼系数C正相关。因此，当阻尼系数C较小时，小震下的刚度位移损失率ηke将小于最优损失率ηke-op。此时，随地震作用增加，刚度位移损失率ηke减小，逐渐远离最优损失率ηke-op，附加阻尼比ζ随地震作用的增大而减小，如图12所示。

当阻尼系数C逐渐增大时，小震作用下的刚度位移损失率ηke逐渐增大，直至大于最优损失率ηke-op。此时，随地震作用增加，刚度位移损失率ηke减小，逐渐接近最优损失率ηke-op，直至小于最优损失率ηke-op，最后逐渐远离最优损失率ηke-op，附加阻尼比ζ随地震作用的增大先增大后减小，如图13所示。

当阻尼系数C足够大时，大震下的刚度位移损失率ηke将大于最优损失率ηke-op，此时小震、中震、大震作用下，刚度位移损失率ηke将一直处于逐渐接近最优损失率ηke-op的过程中，附加阻尼比ζ随地震作用的增大而增大，如图14所示。

5 结论

本文通过引入基于单自由度基本体系的位移损失理论推导和基于实际工程的参数数值分析，得到的主要结论如下：

(1)在基本体系中，存在最优损失率ηke-op，使得当刚度位移损失率ηke=ηke-op时，附加阻尼比ζ取得最优值ζmax。ηke-op的取值与损失刚度比y、变形模式损失率ηd有关。

(2)最优附加阻尼比ζmax与损失刚度比y和变形模式损失率ηd有关。损失刚度比y越大，变形模式损失率ηd越小，则最优附加阻尼比ζmax越大。

(3)实际工程算例中，随阻尼系数C的增加，减震率θ先增大后减小。最优减震率θmax随地震作用变化不明显。框剪结构的θmax明显小于框架结构的θmax。

(4)当阻尼系数C较小时，附加阻尼比ζ随地震作用的增大逐渐减小；当阻尼系数C适中时，附加阻尼比ζ随地震作用的增大先增大后减小；当阻尼系数C较大时，附加阻尼比ζ随地震作用的增大逐渐增大。

(5)实际工程算例中得到的减震率θ变化规律，均与基本体系中附加阻尼比ζ的变化规律相契合。可基于式(14)～(16)推断减震率θ的变化规律。

(6)在进行减震结构设计时，应综合小震、中震、大震作用下的减震效果进行设计，保证减震结构在中震、大震作用下的安全储备。避免因片面追求小震下的减震效果而导致中震、大震作用下的安全储备降低。