7A04 铝合金矩管压弯构件稳定性有限元分析
刘佳钰,吴沛峰,张 成,胡耀伟,张若瑜,3
[1.中国市政工程华北设计研究总院有限公司,天津市300074;2.天津大学建筑工程学院,天津市300072;3.滨海土木工程结构与安全教育部重点实验室(天津大学),天津市300072]
0 引 言
铝合金材料具有耐腐蚀、密度小、加工性能好、维护费用低和易于再生等优点,早在20 世纪初就已经应用于国外的桥梁结构,因此国外对铝合金构件稳定性方面的研究较为成熟,各国规范比较完善。进入21 世纪,铝合金在国内的桥梁结构中也逐渐得以应用,且多以桁架结构为主。相比于钢和混凝土组合桥梁,铝合金桥梁具有经济美观、施工速度快、防腐蚀性能好、可循环利用等优点。然而目前国内对铝合金压弯构件稳定承载力研究较少,并以6 系铝合金为主。郭小农等[1]进行了6061-T6 铝合金偏心受压试验,拟合出了计算三类截面偏压构件弯曲失稳的公式。张铮等[2-3]对H 形截面压弯构件的平面内、平面外承载力进行研究,提出了压弯构件稳定承载力的计算公式。翟希梅等[4-5]进行了箱形截面和L 形截面6082-T6 铝合金偏心受压试验,并与中欧规范进行对比,结果表明规范计算公式相对保守,对中国规范L 形截面计算公式进行了修正。李剑彬等[6]对6061-T4 铝合金方管压弯构件平面内稳定性进行有限元分析,基于参数化分析建议对规范中计算公式的修正系数进行了修改。王元清等[7-8]对7A04 铝合金L 形截面柱和大截面角形柱进行轴压整体稳定性能试验研究,结果表明我国规范过多考虑局部屈曲对构件的影响,从而低估了其稳定承载力。现阶段对于铝合金桥梁的设计,《铝合金结构设计规范》(GB 50429—2007)推荐的5 系和6 系铝合金,其设计强度不超过200 MPa,低于Q235 钢材的设计强度,材料强度较低。作为Al-Zn-Mn-Cu 超硬铝系高强度合金,7A04 高强铝合金抗拉强度可达600 MPa,接近Q420 钢材的材料强度,但密度仅是钢材的1/3。因此,7A04 高强铝合金可以有效减小构件截面,减轻结构自重,更符合桥梁结构的材料要求。目前仅有对7A04 轴压构件稳定性的研究,缺少对7A04 压弯构件的研究。本文以7A04 铝合金矩管为研究对象,建立偏心受压有限元模型,分析初始缺陷幅值对于模型稳定承载力的影响,并通过已有轴压试验对有限元模型进行验证。在此基础上,考虑长细比、高宽比和荷载偏心率的不同进行参数化分析,获取压弯构件稳定承载力模拟数据,并与规范进行对比,对规范中压弯构件稳定承载力计算公式进行修正。
1 有限元模拟
1.1 建立有限元模型
基于王衬心的7A04 轴压稳定性试验[9]建立有限元模型,以两端铰接的圆管为研究对象,截面直径为70 mm 和75 mm,厚度为5 mm。材料本构关系采用Ramberg-Osgood 模型[10],即,式中:ε 为应变;σ 为应力;E 为弹性模量;f0.2为屈服强度;n 为应变硬化指数。Ramberg- Osgood 模型与材性试验结果吻合较好,适用于描述7A04 铝合金的本构关系[11]。其中的n 以传统两点法确定,即n=ln 2/ln(f0.2/f0.1),式中f0.1为以塑性应变0.1%规定的非比例延伸强度。模型采用S4R 壳单元,加载方式采用位移加载,非线性屈曲分析时引入初始缺陷,采用通用分析步进行分析,得到稳定承载力。
1.2 验证有限元模型
为验证有限元模型,选用文献[9]提供的9 个7A04铝合金圆管轴压试验数据进行对比验证。采用文献中提供的材性试验数据,弹性模量取 72 195.5 MPa、屈服强度为505.61 MPa、极限强度为572.25 MPa、应变硬化指数为33.75。
图1 为有限元分析结果与文献[9]中试件破坏形态的比较,结果表明有限元模型破坏形态为整体弯曲失稳,与试验结果相吻合。图2 为数值计算结果与文献[9]中试验荷载- 位移曲线的对比,可以看出数值计算的荷载- 位移曲线与试验曲线吻合良好。表1 为数值计算稳定承载力与试验测得的稳定承载力的比较。由表1 可见,两者的平均误差为0.92%,最大相对误差为4.07%。通过以上对比可知,两者结果相近,表明有限元模型模拟7A04 铝合金圆管轴压试验效果良好,建模方法合理,因此可以继续进行7A04 铝合金方管压弯承载力的有限元分析。

图1 有限元分析与试验的破坏形态对比
2 参数化分析
由于目前缺乏7A04-T6 铝合金方管压弯构件的试验结果,合理的数值模拟结果能够为稳定承载力公式提供依据。因此进行参数分析,考虑长细比λ、偏心率e′和偏心方向的影响,获得相应的数值计算结果。有限元模型的材料属性采用文献[11]中的材性试验结果,研究对象为铝合金挤压型材构件,残余应力影响忽略不计。初始缺陷取L/1000(涵盖铝合金构件的几何缺陷和力学缺陷)[3],符合《铝合金建筑型材》(GB/T 5237—2017)中的要求,构件参数设置见表2。
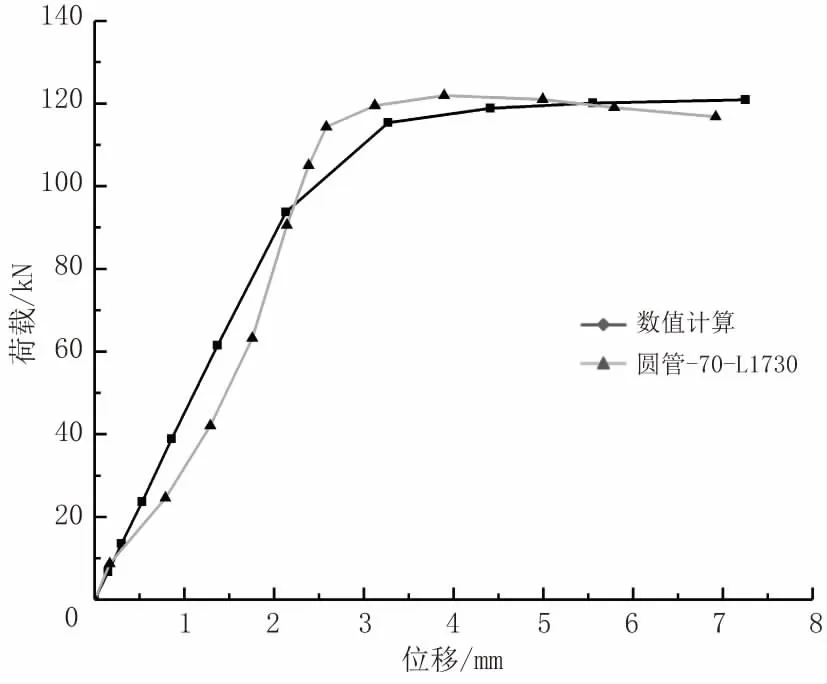
图2 数值计算与试验荷载- 位移曲线对比
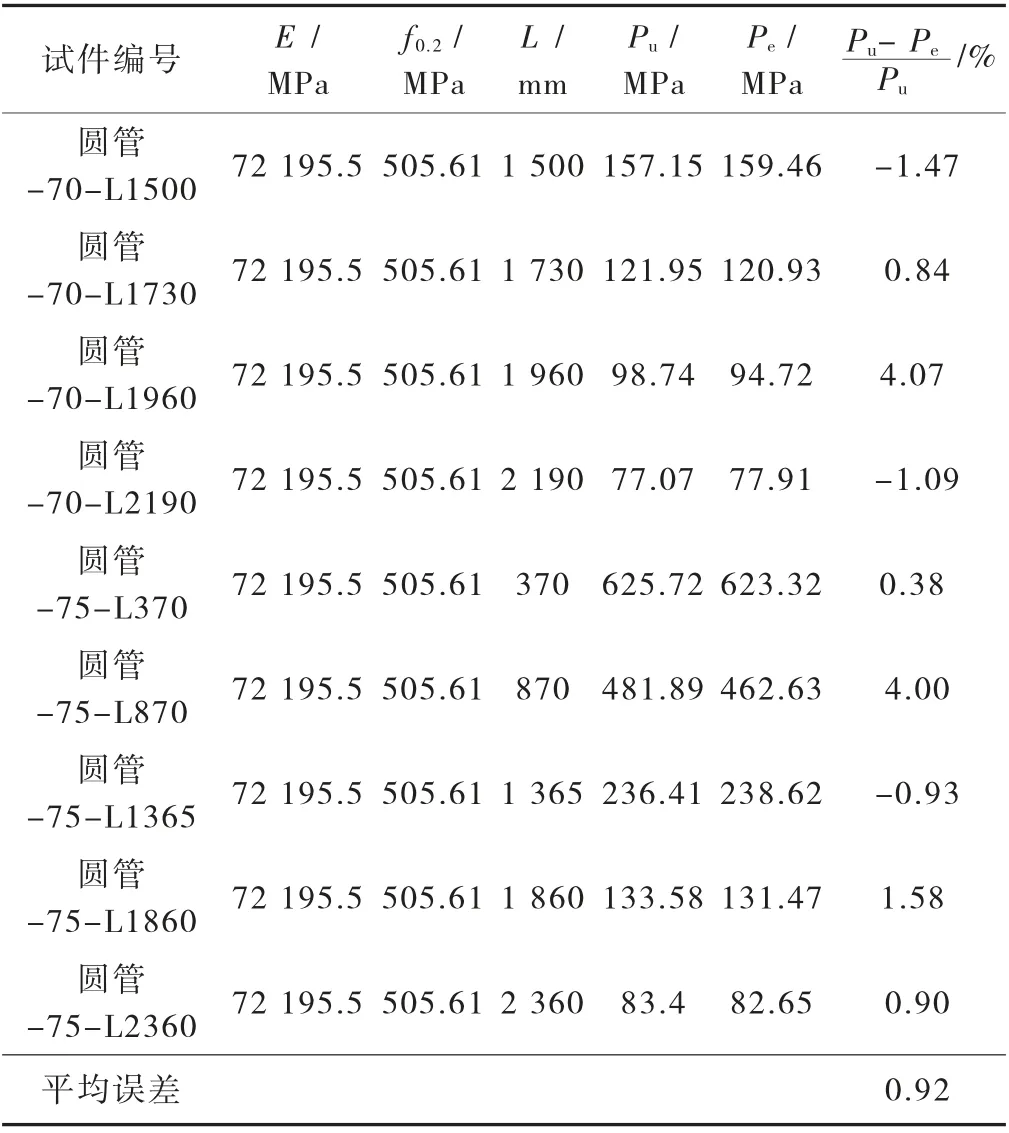
表1 数值计算结果与试验承载力对比
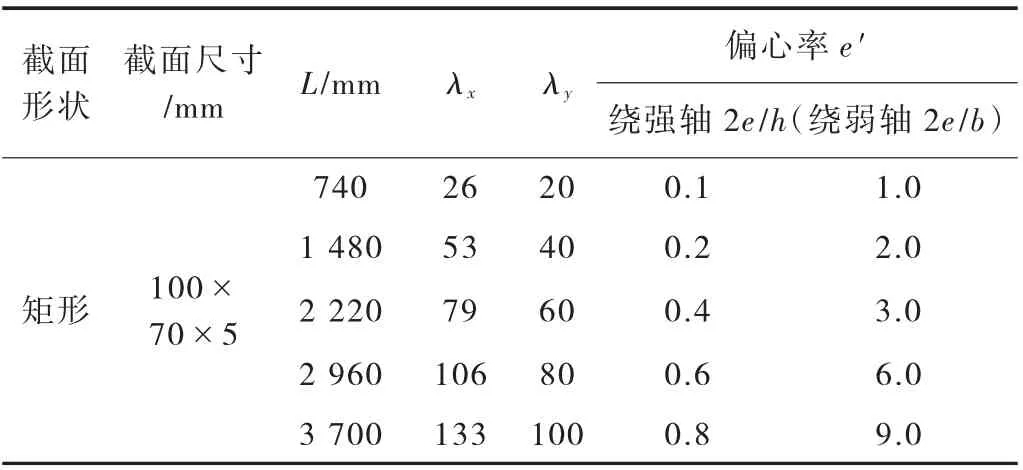
表2 构件参数
初始弯曲方向均为绕弱轴弯曲。由于压弯构件存在轴力N 和弯矩M,两者相互关联,需要研究相关曲线的变化。不同长细比下的绕弱轴偏心的相关曲线见图3,不同长细比下绕强轴偏心的相关曲线见图4。图中纵坐标y=N/(φNy),Ny= f0.2A;横坐标x=M/(φbM*),M*= f0.2W1x,其中N 为数值计算的极限轴力;M 为极限弯矩;A 为截面面积;W1x为弯矩作用平面内的弹性界面模量;φ 为轴心受压稳定系数;φb为受弯构件整体稳定系数。结果表明:矩形构件绕弱轴偏心时发生平面内失稳,相关曲线近似于直线;矩形构件绕强轴偏心,λy=20 时全部发生平面内失稳;当λy=40 时,偏心率e′<0.2 发生平面内失稳,e′>0.2 发生平面外失稳;当λy=60 时,e′<1.0发生平面内失稳,e′>1.0 发生平面外失稳;当λy=80时,e′<2.0 发生平面内失稳,e′>2.0 发生平面外失稳;当λy=100 时,e′<6.0 发生平面内失稳,e′>6.0发生平面外失稳。λy在[20,60]范围内,相关曲线变化明显;λy在[80,100]范围内,相关曲线基本重合。
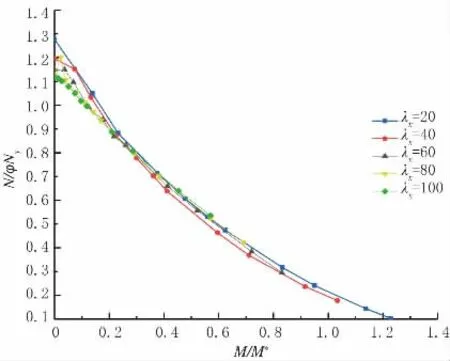
图3 构件绕弱轴偏心相关曲线
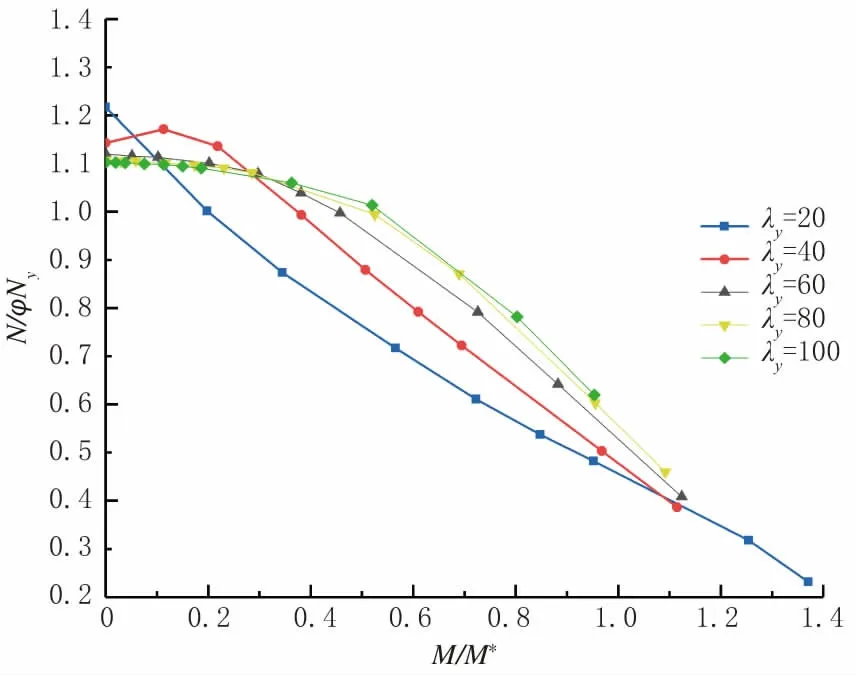
图4 构件绕强轴偏心相关曲线
3 压弯构件稳定承载力计算方法
3.1 《铝合金结构设计规范》计算方法
《铝合金结构设计规范》(GB 50429—2007)(以下简称《规范》)中压弯构件稳定性承载力计算公式为:
矩形截面为双轴对称截面,故稳定计算系数由式(3)进行计算。
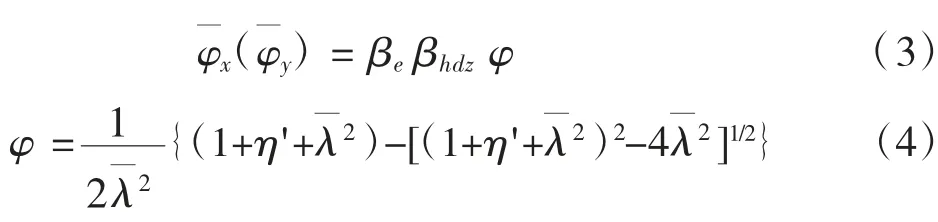
式中:βe为考虑局部屈曲影响系数,本文取1.0;βhdz为焊接缺陷影响系数,本文取1.0;为正则化长细比;η' 为构件几何缺陷系数,η'=α(-),本文α=0.2,=0.15。
3.2 《规范》计算值与数值模拟值的对比
有限元分析结果表明:矩形铝合金压弯构件绕弱轴发生平面内失稳,平面内稳定承载力低于平面外稳定承载力,用式(1)进行计算;绕强轴的构件存在平面内失稳与平面外失稳,稳定承载力采用式(1)与式(2)中较小值进行计算。将有限元分析结果与《规范》计算结果进行比较,平面内公式对比结果见图5,平面外公式对比结果见图6。由图5、图6 可知,数值模拟值全部位于《规范》公式计算值上方,表明《规范》中压弯构件建议计算公式对于7A04-T6铝合金压弯构件计算结果相对保守,适用性较差,需要进行修正与改进。
4 结 论
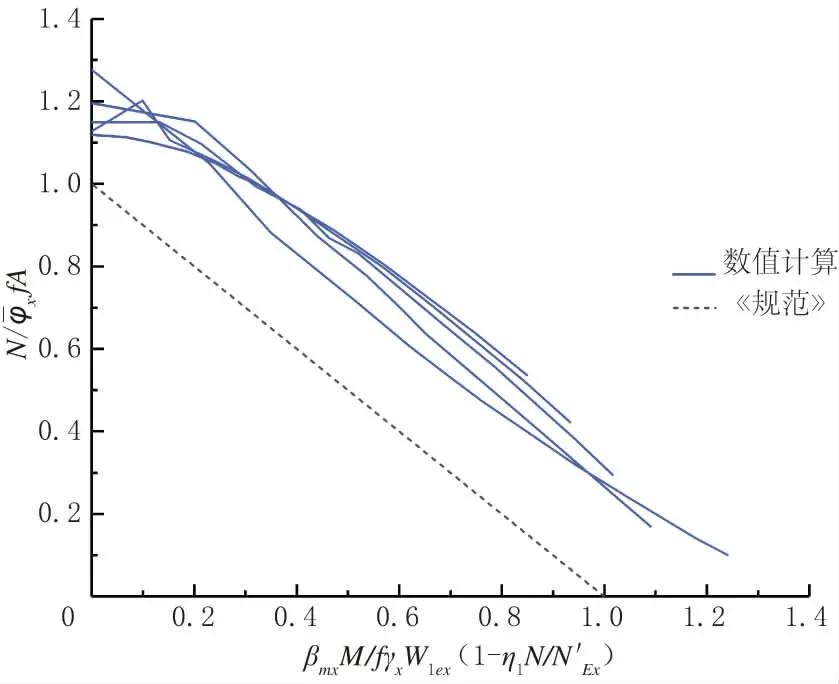
图5 平面内公式对比结果
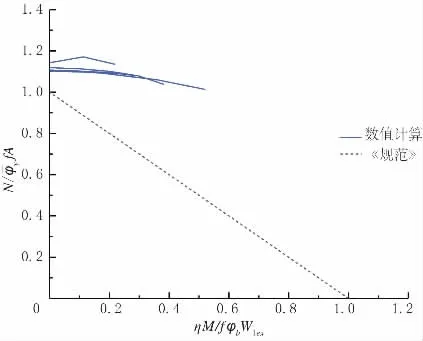
图6 平面外公式对比结果
(1)利用Abaqus 软件,验证了有限元模型的可行性,在此基础上分析出7A04-T6 铝合金矩形压弯构件稳定承载力、失稳模态和变形性能。
(2)进行参数分析,得到压弯构件绕弱轴偏心和绕强轴偏心的相关曲线,在不同长细比下绕弱轴偏心的相关曲线基本重合,绕强轴偏心的相关曲线在λ<60 时变化明显,在λ>60 时基本重合。压弯构件绕弱轴偏心全部发生平面内失稳;对于绕强轴偏心小长细比的压弯构件,在小偏心的情况下会发生平面外失稳,而大长细比构件在大偏心的情况下也会发生平面外失稳。
(3)将数值计算结果与《规范》计算结果进行对比得到相关曲线,结果表明数值计算结果高于《规范》计算结果。说明《规范》建议公式保守,不适用于7A04-T6 铝合金压弯构件的计算,需要进行改进和修正。

