1960～2019年静海高温天气变化特征分析及日高温概率模型

年飞翔， 王丹丹

(1.天津市气象信息中心，天津 300000；2.天津市静海区沿庄镇综合服务中心，天津 300000)

引 言

联合国政府间气候变化专门委员会(IPCC)2013年发布的评估指出，1880～2012年全球平均气温上升了大约0.85℃，1983～2012年的30年间气温连续刷新了最高纪录[1]。在全球气候变暖及国内城市化程度不断加深的背景下，区域范围内极端天气事件发生的频率和强度不断增加。其中，高温天气事件严重影响了居民的日常生活和身体健康，许遐祯等[2]的研究表明，持续的高温热浪可导致人群超额死亡率>20%。同时，高温天气对交通出行、环境空气质量、农业生产等都有严重的影响。研究表明，当气温高于28℃时，事故密度随温度的增加明显增大(潘娅英等[3])；周湘婷等[4]的研究表明，夏季持续高温干旱对PM2.5质量浓度有显著影响；气候变暖背景下，虽然作物生长季的热量资源增多,但高温热害、干旱灾害发生更频繁使热资源的有效性降低[5]。

目前，国内外不同领域的学者对高温天气均有研究，研究主要可以分为3个方向。第一方向为对高温天气变化趋势、时空特征的研究，如IPCC对全球气候变化的评估，严中伟等[6]对中国近几十年极端气候变化的研究，谈建国等[7]对我国主要城市高温热浪时空分布特征的研究。第二个方向为对高温天气产生原因的研究，如Hadley环流强度与中国东部气温相关性的研究[8]，我国北方地区夏季气温异常原因的研究[9]。第三个方向为高温天气事件对各领域活动影响的研究，如陈超等[10]对四川省水稻高温热害风险及灾损进行评估评估，构建了高温热害风险模型；赵琳等[11]分析了海南省不同人群对高温热浪及其影响的适应。

已有对高温天气变化趋势、时空特征的研究多采取对极端最高气温、高温日数和高温热浪指标等变化趋势及危害特征的分析[12～16]，或联合多个极端高温指标对极端高温天气变化进行研究[17]，但对每日高温天气发生概率的研究较少。因此，有必要研究每日高温天气发生概率，以期制定合理应对高温天气的策略，最大程度减小高温天气可能带来的风险与灾害。本文以天津静海为例，研究近60年高温天气事件的变化特征，每日高温发生的统计概率，构建日高温概率模型，为制定减小高温影响、防止高温灾害措施提供参考。

1 资料与方法

1.1 资料

所用资料包括1960～2019年天津市静海国家气象站日最高气温资料。

1.2 高温日和高温热浪

根据中国气象局高温预警发布标准，定义日最高气温大于等于35℃的天气为高温日，n个连续高温日为1次高温天气过程，连续3天以上的高温天气过程称之为高温热浪或高温酷暑。

1.3 Mann-Kendall(MK)趋势检验

Mann-Kendall(MK)检验的目的是统计评估变量随着时间变化是否有单调上升或下降的趋势。单调上升(下降)的趋势意味着该变量随时间增加(减少)，但此趋势可能是、也可能不是线性的。MK检验不要求数据是正态分布，也不要求变化趋势一定是线性的，同时也不受少数异常值的干扰[18-19]。计算方法如下：

(1)

(2)

其中Sn是第i时刻数值大于j时刻数值个数的累计数。E(Sn)，var(Sn)是累计数Sn的均值和方差，计算方法如下：

(3)

(4)

1.4 Levenberg-Marquardt 算法

Levenberg-Marquardt 算法是一种非线性优化方法，即寻找使得目标函数值最小的变量的方法，该方法是D.W.Marquardt在 K.Levenbevg的研究基础上发展而来的[20-21]。该方法是对梯度下降法和Gause-Newton法加以改进的一种方法，通过在高斯牛顿法的迭代公式中引入阻尼因子μ来调节算法的特性，迭代公式如下：

(5)

x为参数向量，f(x)为求极小值的目标函数， Jf为函数f(x)的一阶偏导矩阵，I为单位向量。

阻尼因子μ>0能保证系数矩阵正定，从而确保迭代的下降方向；当μ很大时，该方法接近梯度下降法；当μ很小时，则接近高斯牛顿法，从而使得接近解时快速收敛。在本研究函数拟合中，通过该算法得到使函数计算值与实际值之间误差最小时的参数。

2 结果与分析

2.1 高温日数年际变化

对近60年逐日最高气温进行统计发现，年高温日数平均值为10.3天；年高温日数最多为31天，出现在1997和2000年；年高温日数最少为2天，出现在1979年。 1960年以来出现40摄氏度以上高温日数为6天，其中最高温度为41.6摄氏度，出现在2000年7月1日。由图1年高温日数变化趋势线可知，1960年以来静海年高温日数总体呈上升趋势，利用Mann-Kendall法对高温日数做进一步趋势检验(图1(b))发现，静海1964年至2000年间除1972、1974、1975三年外，UF曲线值均小于0，年高温日数呈下降趋势。其中，1964～1990年UF值均未超过0.05显著水平临界值，年高温日数下降趋势未达到显著水平；1991～1996年UF值在0.05显著水平临界值上下波动，年高温日数下降趋势基本达到显著水平；1997年开始UF值快速增加，下降趋势减弱。2001年开始UF值大于0，年高温日数表现出上升趋势。2014年UF、UB曲线在两临界线之间存在交叉，表明年高温日数的突变时间从2014年开始，此后，年高温日数呈现明显的上升趋势。通过计算每20年的年平均高温日数发现，1960年至1979年年高温日数平均值为8天，1980年至1999年年高温日数平均值为9.6天，2000年至2019年年高温日数平均值为13.7天，近20年年高温日数增加明显。同时，利用Mann-Kendall法对年最高气温做趋势检验发现(图1(c))，1964～2001年UF值小于0，表明1964～2001年静海年最高气温呈下降趋势；2002年以后UF值大于0，年最高气温变为上升趋势；但相较于年高温日数，年最高气温的UF、UB曲线在两临界线之间存在多处交叉，没有出现明显的突变点。

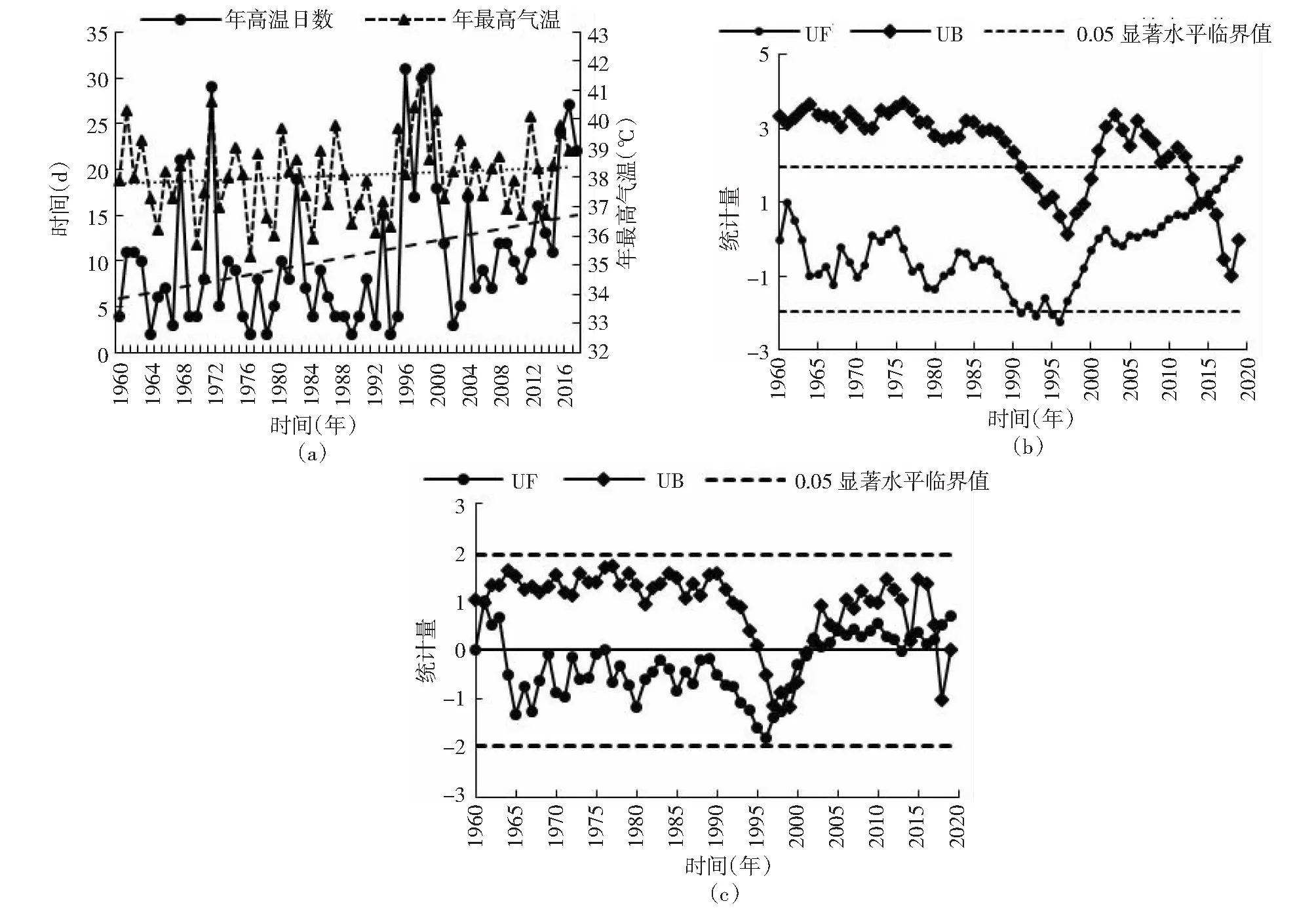
图1 年最高气温、年高温日数年际变化(a)及Mann-Kendall统计曲线(b、c)

2.2 高温天气过程持续时间年际变化

对近60年静海逐日最高气温进行统计发现，日最高气温超过35℃的高温天气共出现627天，共374次高温天气过程，其中最短持续时间为1日，最长持续时间为9日。1960年以来，静海发生的高温天气过程中持续1日的高温天气过程共232次，年均出现3.9次，占比最高，为62%；占比第二的为持续2日的高温天气过程，共发生85次，年均出现1.4次，占总高温天气过程的22.7%；持续3日及以上的高温天气过程共发生57次，年均出现次数约为1次，占总高温天气过程的15.3%。如表1所示，1960年以来静海共出现高温热浪23次，其中持续时间为9日的高温热浪共2次，分别出现在1997年7月20日至28日、1999年6月24日至7月2日；出现持续时间为8日的高温热浪过程1次，时间为1999年7月23日至30日；出现持续时间为6日和7日的高温热浪各2次，出现持续时间为5日和4日的高温热浪分别为7次、9次。统计可知，1960年至1979年高温热浪共发生3次，1980年至1999年发生6次，2000年至2019年发生14次，近20年高温热浪发生次数增加明显。

表1 1960至2019年静海高温热浪发生日期及持续时间

2.3 高温开始及结束时间的年际变化

了解高温开始和结束时间对高温天气气候预报、高温灾害防治、农作物栽培管理都有重要意义。从图2中可以看出，静海高温日开始时间最早出现在5月7日，最晚出现在7月20日，平均出现时间为6月13日；高温日结束时间最早出现在6月20日，最晚出现在9月8日，平均出现时间为7月30日。静海高温日开始时间及结束时间年际间变化均较大，高温日开始时间标准偏差为13天，结束时间标准偏差为18天，高温日结束时间年际间变化大于开始时间年际间变化。图中趋势线可以看出，近60年高温日开始时间有提前的趋势，气候倾向率约为1.4d/10a；高温日结束时间有明显推迟的趋势，气候倾向率约为4.8d/10a，说明静海可能出现高温日的时间区间越来越长。

2.4 日高温发生概率及模型模拟

通过统计静海近60年某日最高气温超过35℃的发生次数，计算得到某日最高气温超过35℃的频率，即一年中某日最高气温超过35℃的发生概率。静海近60年5月7日以前及9月8日以后均未出现日最高气温大于35℃的天气，一年中日最高气温可能超过35℃的时间为5月7日至9月8日，在此时间段内随时间推移每日高温发生概率整体表现出先增高后降低的特点。每年6月中旬至7月中旬为日高温发生概率相对较高的时段，其中6月16日、6月24日、7月4日为60年中高温发生统计概率最高的3天，同时受到夏季降水影响该时段内每日高温发生概率波动较大，而其他时段日高温发生概率变化趋势则较稳定。

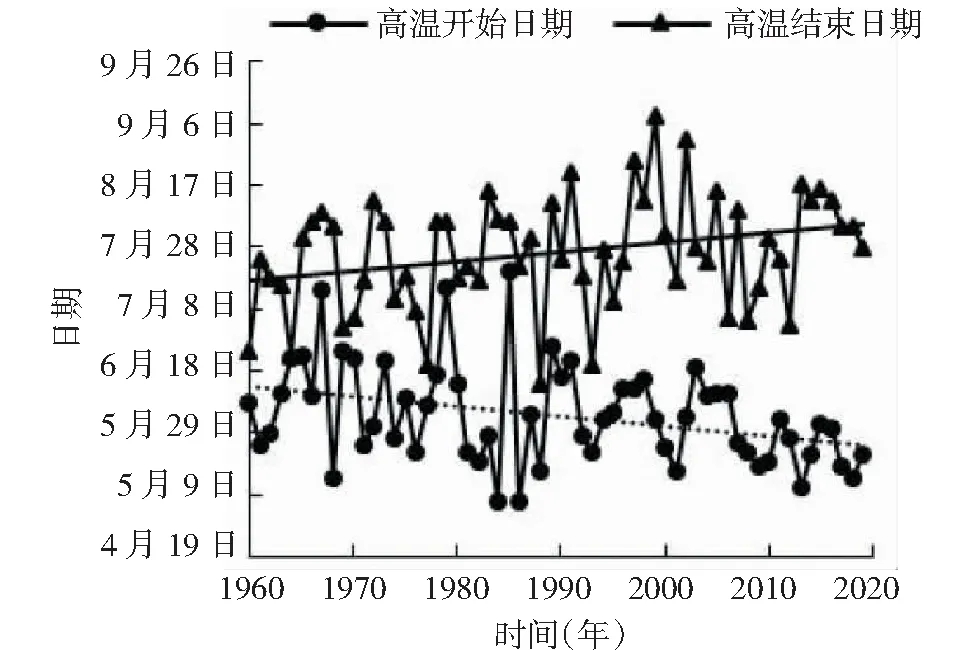
图2 1960至2019年静海高温开始及结束时间的年际变化

模拟模型可以通过提取系统或过程的特性，用数学方程定量表示系统结构与功能随时间变化规律，从而简化实际问题，使系统或过程更便于研究与应用。构建每日高温发生概率的模型可以更加直观描述其变化规律，对于高温预报、高温灾害风险评估、农业生产均有重要作用。通过上文分析可知，从高温开始发生起，日高温发生概率变化特点与“钟型”曲线相似，因此本文通过下式函数(模型1)对日高温发生概率进行模拟：

(6)

其中pi为日高温发生概率；x为可能发生高温时段内的天数，历史上最早出现高温的日期为1；α、β、γ为模型参数。

利用Levenberg-Marquardt 算法对模型函数进行拟合，使模型均方误差达到最小，得到模型的最优参数如下表2。从图3中模拟值1可以看出，模型曲线较好的表现出了日高温发生概率随时间的变化趋势，但是在每年6月中旬至7月中旬日高温发生概率相对较高且概率波动较大的时段，模型无法模拟概率波动的规律，只能表现其平均状态。由于日高温发生概率的波动主要受到降水的影响，而降水由气候背景和天气系统决定，因此通过引入主要气候背景和天气系统的发展变化规律即可进一步细化日高温发生概率的变化特点。

表2 模型参数表1

傅里叶的研究表明，任何连续周期信号都可以由一组适当的正弦曲线组合而成。虽然正弦曲线无法组合成一个带有棱角的信号。但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别。数学家傅里叶发现：任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。假设日高温概率为一组周期变化的气候背景或天气系统影响及噪声的叠加，每一个周期变化的气候背景或天气系统的影响均可由适当的正余弦曲线来表示。因此，日高温概率函数可以用傅里叶级数来表示，其指数形式为：

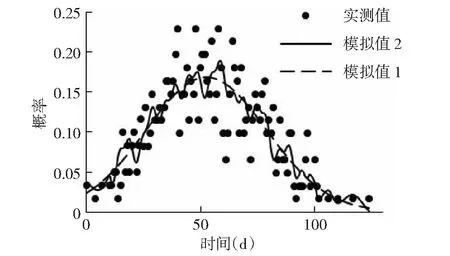
图3 实测值与模型模拟值对比

(7)

P为高温概率，t为时间，F为系数，i为虚数单位，T为周期，n=1，2，……∞。

日高温概率函数的傅里叶级数实值形式(三角级数)可以写成：

(8)

其中αn和βn是实频率分量的振幅，C为常数，其他同上式。

由欧拉公式可以将公式(8)中的一组正余弦函数表示成与模型1相同的指数形式，保留其年际变化特征，公式如下：

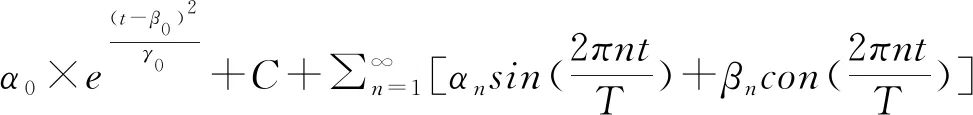
(9)

α0、β0、γ0为模型参数，其他同上式。

理论上越多的频率分量越能准确的表达概率的变化规律，但是较多的频率分量并不利于实际使用，因此通过对日高温发生概率的时间序列进行傅里叶变换找出其振幅较高频率，过滤振幅较低的频率及噪声，并选取除以年为周期的分量外的其他振幅最高的4种频率fi(周期1/fi)进一步模拟日高温概率函数。由于相同周期余弦函数可以表示成相位不同的正弦函数，可以将公示(9)简化成如下形式(模型2)：

(10)

(11)

α、C为模型参数，f为频率，i=1，2，3，4，其他同上式。

利用Levenberg-Marquardt 算法对模型函数进行拟合，使模型均方误差达到最小，得到模型的最优参数如表3。

表3 模型参数表2

由图3中模拟值2可以看出，模型2在整体趋势上同实际值及模型1相同，即模型函数中的低频分量能较好的反映日高温概率在年尺度上的变化特点。同时，由于模型2增加了4个正弦函数，模型中的高频分量对短周期的天气系统变化有了更好的模拟能力，丰富了模型对细节的表达能力，使其更加符合日高温概率的实际变化情况。

3 结 论

本文对近60年静海逐日最高气温进行了统计，分析了高温日数年际变化、高温天气过程及持续时间变化、高温开始及结束时间的年际变化、日高温发生概率，构建了日高温发生概率模型，结论如下。

3.1 近60年静海年高温日数平均值为10.3天，最早出现高温的日期为5月7日，最晚出现高温的日期为8月25日，日最高温度为41.6℃，出现在2000年7月1日。Mann-Kendall趋势检验结果表明，1960年至1996年静海年高温日数呈下降趋势， 1997年开始年高温日数呈上升趋势，但均未达到显著的水平。同时，利用Mann-Kendall检验表明，1960年以来静海年最高气温无明显的上升的趋势。

3.2 近60年静海共发生374次高温天气过程，其中最长持续时间为9天，分别出现在1997年7月20日至28日、1999年6月24日至7月2日。所有高温天气过程中持续一天的占比最高，为62%，年均出现3.9次；近20年高温热浪发生次数较前两个20年增加明显。

3.3 静海高温日开始时间最早出现在5月7日，最晚出现在7月22日，平均出现时间为5月29日；高温日结束时间最早出现在6月20日，最晚出现在9月16日，平均出现时间为8月5日。近60年高温日开始时间有提前的趋势，气候倾向率约为1.4d/10a；高温日结束时间有明显推迟的趋势，气候倾向率约为4.8d/10a。

3.4 每年6月中旬至7月中旬为静海日高温发生概率相对较高的时段，其中6月16日、6月24日、7月4日为60年中高温发生统计概率最高的3天。“钟型”曲线模型较好的表现出了日高温发生概率随时间的变化趋势，但对日高温发生概率相对较高且概率波动较大的时段模拟能力不足；通过分解日高温发生概率各频率分量，改进后的模型提升了对概率波动的模拟能力。