军民融合PPP模式的演化博弈及动态仿真研究
徐 刚,何文刚,马大来,石良娟,何 岚
(重庆理工大学 管理学院,重庆 400054)
一、引言
军民融合发展作为一项国家战略,担负着推动军队现代化建设和经济发展的重担,现阶段已进入到深度融合、实现跨越式发展的关键时期。党的十九大报告指出:“深化国防科技工业改革,形成军民融合深度发展格局,构建一体化的国家战略体系和能力。”2017年11月,国务院印发《关于推动国防科技工业军民融合深度发展的意见》,该战略聚焦核心技术突破和重大基础设施建设,需大量资金作为保障[1]。然而我国国民经济增速由高速转为中高速增长,使财政压力增大,国防费用支出空间变小[2]。在我国深化军队改革、周边安全形势严峻的新形势下,军民融合资金问题严重制约该战略发展,“十三五”规划纲要已明确提出要“探索建立军民融合项目资金保障机制”。2016年6月,中共中央、国务院、中央军委印发的《关于经济建设和国防建设融合发展的意见》指出:要发挥市场作用,注重运用市场手段优化军地资源配置,积极引导经济社会领域的多元投资、多方技术、多种力量更好服务国防建设,促进国防建设成果更好服务经济社会发展,实现经济建设和国防建设综合效益最大化。政府与私人部门合作的PPP模式在我国发展势态好、增长快、优势大、前景广、能兼顾经济和社会效益[3],具有利用新技术、机制创新、引进管理经验和创新融资方式的职能[4-5],适应军民融合发展创新需求、适用军民融合多个领域[6]、能提高民参军的积极性[7]。目前以PPP模式推进军民融合仍面临挑战,但却是解决军民融合项目资金问题的有效措施,意义重大[8]。
近年来,学者们对于军民融合领域资金保障问题进行了较多研究。一是多元化融资机制方面。张燕等基于军工企业发展资金、社会资源配置需求和国家政策角度,认为我国军工企业发展必然采取多元化融资策略[9];纪建强等认为变革后的国防科技工业融资机制仍不完善,提出构建军民融合融资机制和采取多种融资手段的建议[10];林颖等提出构建军民融合发展基金支持体系以满足军民融合领域资金需求[11];董小君等分析了我国军民融合金融支持体系的现状,提出构建包含分阶段实施、拓宽融资渠道、完善保障机制等多元化资金支持体系[12];周全等认为金融能促进军民产业融合,结合国外经验提出发展多层次金融资本市场、完善保障和运行机制等建议[13]。二是军民融合PPP模式应用方面。陈胜探究了军民融合发展应用PPP模式的可行性,认为PPP模式应用到军民融合发展中既可行又有效[14];刘尚希等认为以PPP模式推动军民融合,有利于军事和经济发展,但推广应用存在一些待完善的问题[8];冯海斌等分析了军事装备基地维修服务PPP模式采购的有利条件和重大作用,构建了军事装备维修领域PPP模式的基本框架和运作流程[15];肖月鑫等探索了军事物流基地建设中应用PPP模式的框架构想及支撑机制,并基于我国当前现状提出相应建议[16];位珍珍介绍了PPP模式的内涵和在国防项目中的应用模式,总结英国国防PPP模式案例的成功经验为我国军事院校改革提供参考[17]。
演化博弈理论假定博弈双方是有限理性的,它将博弈分析和动态演化过程结合起来探索群体动态演化过程和演化稳定策略。目前,演化博弈研究比较成熟,多位学者使用该理论研究PPP模式和军民融合相关问题。徐刚等构建网信军民融合信息共享博弈模型,研究信息共享因素和奖惩机制对军民双方信息共享行为的影响[18];方炜等基于演化博弈理论研究了军民融合协同创新过程中的协同合作稳定性问题[19];蒋铁军等运用演化理论构建了互补性技术合作博弈模型,分析军民技术合作演化博弈过程[20]。杨晓东等构建政府群体和投资群体演化博弈模型,研究用PPP模式绿色改造老旧建筑的问题[21];程敏等结合系统动力学和演化博弈方法研究了邻避设施PPP项目中博弈主体的行为策略和影响因素[22]。
以上研究对于丰富军民融合理论和实践做出了一定贡献,但也存在不足:(1)研究多集中于从宏观层面研究军民融合融资机制,较少从微观层面研究PPP模式的影响因素及影响程度;(2)研究方法均为定性分析,缺乏定量研究方法。因此,本文以军民融合领域融资主体为研究对象,构建军民行为策略博弈模型,并使用系统动力学方法对双方行为趋势进行仿真和分析,探究军民融合PPP模式中军口单位和民口单位的演化博弈过程、影响因素和影响程度。本文内容有利于丰富军民融合PPP模式相关理论研究,为军民融合领域制定金融服务政策和“民参军”政策提供了参考。
二、军民融合PPP模式应用范围
PPP英文全称是Public-Private Partnerships,中文译为公私合伙制,指公共部门与私人部门建立合作关系来提供公共产品或服务的一种方式。合作双方具有“利益共享、风险分担、伙伴关系”的特点。PPP模式的本质是吸纳社会优质资本与技术,在公共财政资金短缺或不擅长的领域,发挥其在资本、技术和管理等方面的相对优势。它通过与公共部门合作提供公共产品或服务,与军民融合具有内在一致性。提供准公共产品的军民融合项目可以由国家财政和民间资本共同承担,此类项目既能满足军事效益,也能兼顾社会经济效益,但突出公共性和涉及国家重大安全的核心军事能力建设项目不适用于PPP模式。
PPP模式适用的范围包括:一是不涉及核心军事能力建设,但具有民用转化与市场应用潜力的国防科研项目和创新型技术;二是可共建共用的军民两用基础设施,如军民两用码头、军民两用机场、军民两用实验室、城市管网建设等;三是装备联合维修保养;四是训练设施共建共用;五是融合式保障服务。无论经济、政治还是军事方面,国防军工领域引入PPP模式都有积极意义。经济方面:能缓解公共财政压力,提高资金使用效率;丰富国防军工领域融资手段,打造国民经济发展新引擎;可以避免基础设施重复建设,提升基础设施使用效率。军事方面:引入市场机制,改善国防设施服务水平和效率,促进管理体制改革与创新;提供项目资金支持,保障国防和军队安全,使军队专注于核心军事能力建设。
三、问题描述与模型假设
(一)问题描述
在适用PPP模式的军民融合项目中,军口单位积极引进民口单位参与国防军工项目,可降低项目建设、管理和维护等成本,转移风险给民口单位。拥有先进技术、充裕资金、丰富管理运维经验的民口单位参与军口单位项目,可获得额外收益,同时需要投入建设、运营等成本和分担项目风险。军口单位和民口单位都是有限理性的,双方根据自己的利益诉求,经过博弈做出最佳策略选择。
(二)模型假设
军口单位、民口单位在军民融合项目中均有两种策略选择。假设民口单位参与项目策略的概率为x(0≤x≤1),不参与项目策略的概率为(1-x);军口单位引进民口单位策略的概率为y(0≤y≤1),不引进民口单位策略的概率为(1-y)。针对双方合作过程中的相互关系及影响因素进行具体分析,本文假设如下:
假设1:项目未采取PPP模式时,民口单位从事以往经营范围内业务时的基本收益之和为ω1(ω1>0),军口单位项目的军事及非军事基本收益之和为ω2(ω2>0)。项目采取PPP模式时超额收益为ω(ω>0),民口单位收益共享比例系数为λ1(λ1>0),军口单位的收益共享比例系数为λ2(λ1+λ2=1)。
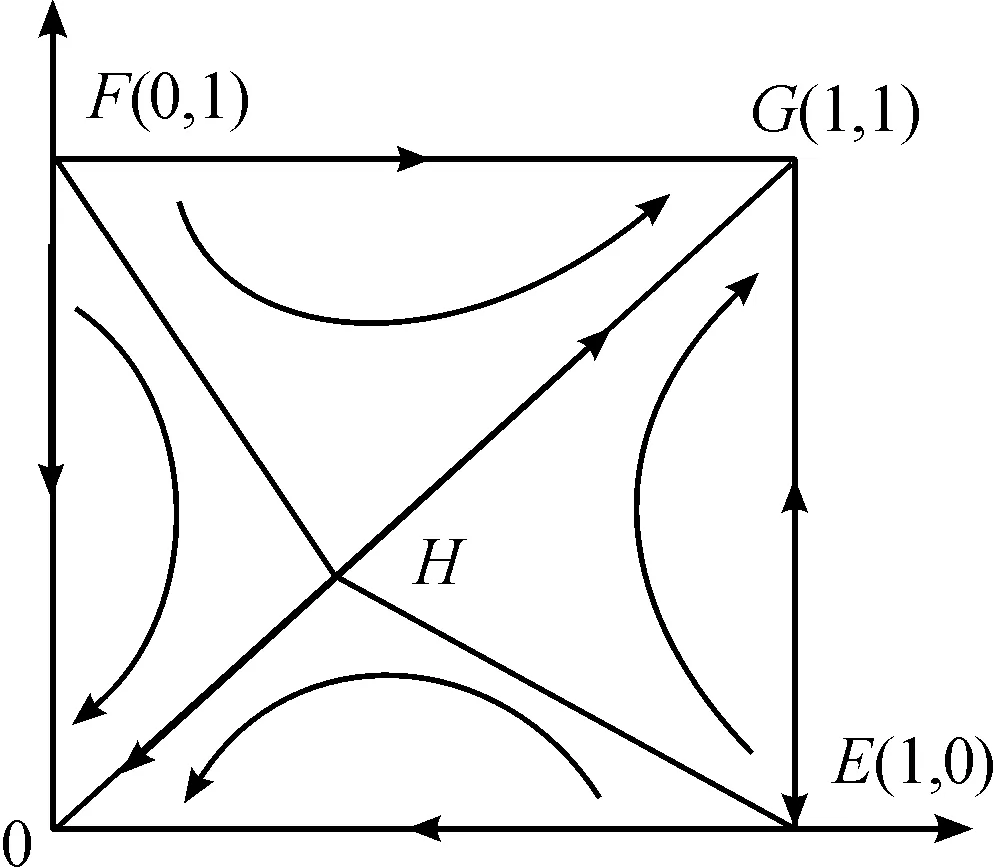
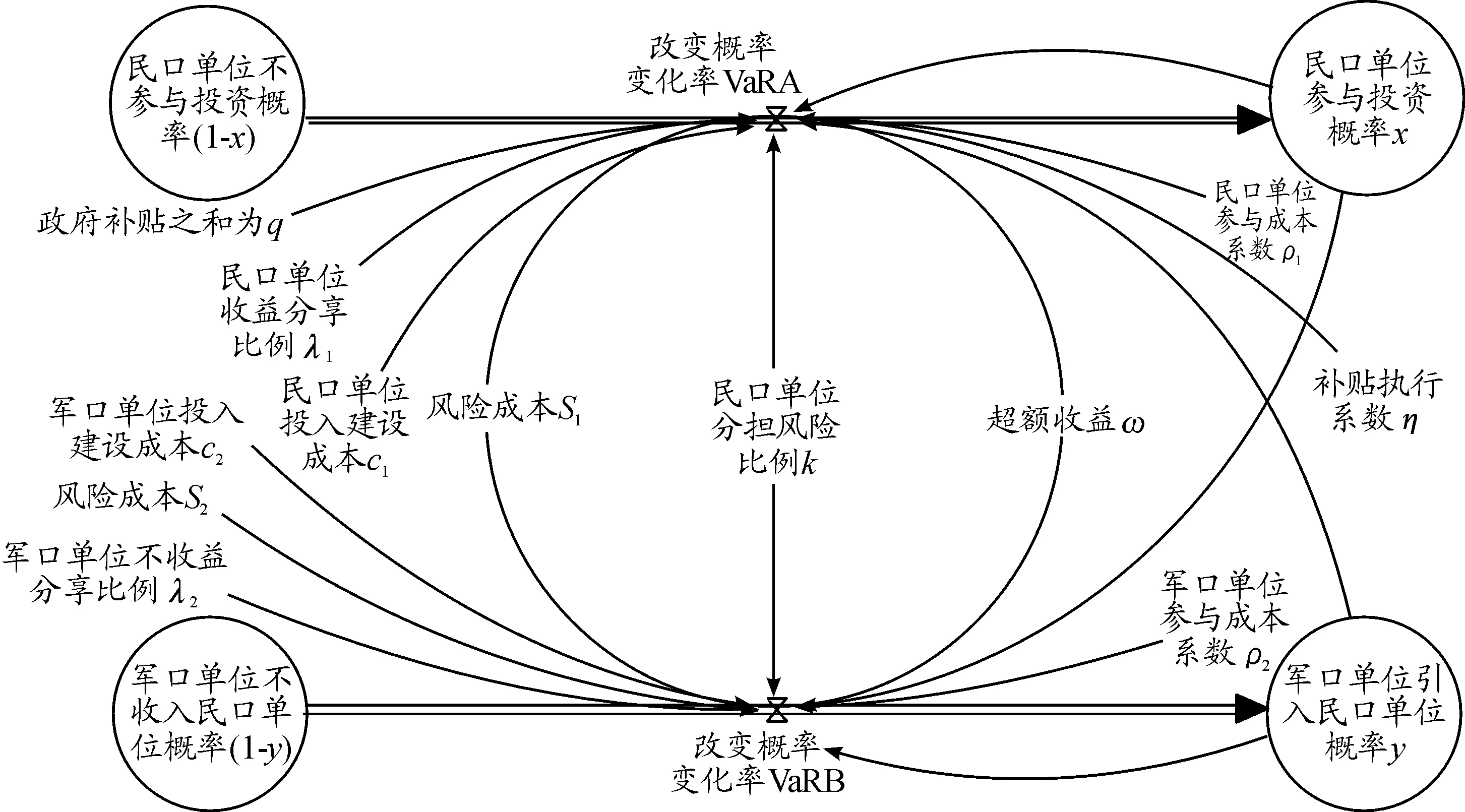
假设2:PPP项目需投入建设、运营、维护等成本,总和记为c(c=c1+c2)。在评估是否采取PPP模式参与项目前,军民双方中考虑采取PPP模式的一方需要投入人力、物力、财力等参与成本。民口单位参与成本系数为ρ1(0<ρ1<1),参与成本为ρ1c1;军口单位参与成本系数为ρ2(0<ρ2<1),参与成本为ρ2c2(0<ρ2c2<ρ1c1)。若项目采取PPP模式时,民口单位分担项目成本c1(c1>0),军口单位分担项目成本c2(0 假设3:PPP项目周期长、投资规模大、参与方多、不确定性高,导致参与主体在合作过程中需要面对巨大的的项目整体风险。Li等基于英国成功PPP项目的分析,认为合适的项目风险分担比例是项目成功的关键因素之一[23]。汪国懋认为合作双方共同承担PPP项目风险,虽使风险更高但能比一方独立承担项目获得更多收益[24]。本文假设双方在签订项目合同时商定项目风险分担比例,项目中后期根据实际情况协商调整。设PPP模式下项目整体风险成本之和为s1,民口单位的风险分担比例系数为k(0 假设4:民口单位参与军民融合PPP项目可获得各级政府政策规章倾斜、税收优惠、专项资金支持等补贴,其和记为q。η(0≤η≤1)表示补贴执行系数,故民口单位获得政府补贴为η×q。 根据问题描述和模型假设得到军口单位和民口单位的收益矩阵,如表1所示。 表1 军口单位和民口单位收益矩阵 当民口单位选择参与项目时的收益为: U11=y[ω1+λ1ω+ηq-c1(1+ρ1)-ks1]+(1-y)[ω1-ρ1c1]= y[(λ1ω+ηq)-(ks1+c1)]+(ω1-ρ1c1) (1) 当民口单位选择不参与项目时的收益为: U12=yω1+ω1(1-y)=ω1 (2) 因此,民口单位的平均收益为: U1=xU11+(1-x)U12=xy[(λ1ω+ηq)-(c1+ks1)]+(ω1-xρ1c1) (3) 则民口单位参与军民融合PPP项目时的复制动态方程为: (4) 同理可得,军口单位引进民口单位参与项目时的复制动态方程为: (5) 演化系统平衡点稳定性可由该系统雅克比矩阵的局部稳定性分析得到。根据Fridman方法,分析判断军口单位和民口单位复制方程所组成系统的稳定性。令A=λ1ω+ηq,B=(s1k+c1),C=λ2ω+c2,D=-s2+s1(1-k),可得其雅克比矩阵为: (6) 雅克比矩阵行列式的值为: (1-2x)(1-2y)[y(A-B)-ρ1c1][x(C-D)-ρ2c2]-xy(1-x)(1-y)(A-B)(C-D) (7) 雅克比矩阵行列式的迹为: (8) 当均衡点使得detJ>0且trJ<0时,均衡点处于局部稳定状态。由detJ和trJ的表达式可知,其值取决于A和(B+ρ1c1)以及C和(D+ρ2c2)的相对大小。因此,分以下4种情况讨论: ① 当A>(B+ρ1c1)且C>(D+ρ2c2),即民口单位和军口单位采取PPP模式的收益均大于成本时,系统稳定状态见表2。 表2 系统稳定性情况1 ② 当A>(B+ρ1c1)且C<(D+ρ2c2)时,即民口单位采取PPP模式的收益大于成本、军口单位采取PPP模式的收益小于成本时,系统稳定状态见表3。 表3 系统稳定性情况2 ③ 当A<(B+ρ1c1)且C<(D+ρ2c2)时,即民口单位和军口单位采取PPP模式的收益均小于成本时,系统稳定状态见表4。 表4 系统稳定性情况3 ④ 当A<(B+ρ1c1)且C>(D+ρ2c2)时,即民口单位采取PPP模式的收益大于成本且军口单位采取PPP模式的收益小于成本时,系统稳定状态见表5。 表5 系统稳定性情况4 通过以上分析可以看出:系统是否处于稳定均衡状态,取决于双方采取PPP模式参与项目的收益和成本,只要其中一方的项目收益小于项目成本时(系统稳定性情况2、3、4),系统收敛于唯一稳定均衡点(0,0),即民口单位∶军口单位={不参与,不引进};仅当双方的项目收益大于项目成本时,双方才会采取合作策略。除了采用detJ和trJ判别均衡点的局部稳定性,还可以运用动态演化相图分析系统收敛于稳定均衡点的变化趋势。图1为系统动态演化相图,描述了PPP项目合作中的动态演化过程。 图1 条件1情况下系统动态演化过程 当初始状态处于区域EHFG时,系统将收敛于稳定的均衡点G,即军民双方合作完成项目;当初始状态处于EOFH时,即民口单位不参与、军口单位选择不引进民口单位参与项目策略。同时,通过EOFH的面积可描述长期均衡策略的概率,具体表示如下: EOFH的面积越大,系统收敛于稳定均衡点G的概率越大,反之收敛于稳定均衡点O的概率越大。 用VensimPLE 5.9建立军民融合PPP项目的演化博弈SD模型,其结构和变量名称如图2所示。 图2 军口单位和民口单位的演化SD模型 系统动力学模型能研究动态反馈系统活动[25],应用领域广泛[26]。仿真运行是为了验证演化博弈模型结果的正确性和有效性。鉴于PPP模式在我国应用时间短和国防军工领域保密严格,模型相关参数既无专业数据库支撑,也难以通过调研等方式获得。对于数据缺失的问题,李天博等认为重要参数影响演化趋势,改变参数能揭示群体间博弈规律[27];Sterman认为仿真的有用性在于可以在一定程度揭示事物的规律而非完全符合现实[28];Wu Desheng等指出系统动力学模型结构的正确性比参数值选择更重要[29]。本文结合PPP模式的特点及博弈条件,对模型中变量进行赋值。参数初始值设置如下:q=1.2,λ1=0.7,λ2=0.3,c2=0.9 ,η=1,ρ1=0.4,ρ2=0.7,c1=2.3,ω=7,s1=3.6,s2=0.4。民口单位作为投入成本大,在项目中主要负责项目建设、运营、维护,风险管理能力和意识比军口单位强,故令k=0.7。以上参数初值设置符合条件1。 (1)军口单位和民口单位初始演化过程 考虑实际情况中项目实施、政策生效时间,设置模型初始时间为0,结束时间为15,演化博弈过程时间单位设为年,时间步长为0.5,可以更好地观察双方的趋势变化。x和y分别代表参与项目、引进民口单位策略的初始概率。为了直观观察军民双方在不同初始状态下的策略概率变化情况,改变双方初始策略概率进行仿真分析。设军口单位引进民口单位策略的初始概率为y=0.5,分别将民口单位参与项目的初始策略x设为20%、40%、70%、90%(分别对应后续图中编号为1、2、3、4的4条曲线)时,观察双方群体的策略概率变化情况,演化结果如图3和图4所示。再令x=0.5,其他参数不变,同理得到演化结果如图5和图6所示。 图3 x初值对民口单位的影响 图4 x初值对军口单位的影响 图5 y初值对军口单位的影响 图6 y初值对民口单位的影响 通过图3—图6可以看出:当y或x的初值固定时,军口单位和民口单位参与PPP项目的演化趋势受其初值影响显著。y初值固定,当x初值较大时,其值会收敛到1,且y受其影响同步收敛到1;当x初值较小时,其值会收敛到0,且y同步收敛到1。当x的初值固定时,亦有相同变化趋势。通过比较图6和图4,图5和3可以看出:在双方初始意愿相同的情况下,军口单位趋于1的速度快于民口单位。同时,仿真结果还表明:x初值越大,x、y收敛于1的速度越快;反之则慢。 结论1:军民双方初始意愿对博弈稳定策略有正向影响。若x或者y初值较小的情况即军口单位或民口单位的积极性不高时,双方难以达成合作;在双方初始意愿均较高的情况下,军口单位比民口单位更快趋于采取PPP模式。 (2)改变收益 不改变其他参数情况下,按照表2的条件将ω=7调整到ω=8,双方的演化博弈结果如图7、图8所示。通过比较图7与图3可以看出:当项目收益增大时,x=0.2的曲线趋于0的速度放缓;x=0.4的曲线趋向发生改变,最终以较快速度趋向于1;x=0.7和x=0.9的曲线以更快的速度趋于1。比较图8与图5可以看出:当收益增大时,y值较大的两条曲线收敛速度加快;y=0.4的曲线从趋于0转向以较快速度趋于1;y=0.2的曲线收敛方发生改变,接近趋于1。 图7 ω=8时民口单位演化结果 图8 ω=8时军口单位演化结果 结论2:项目收益对博弈稳定策略有正向影响。当项目收益较大时,民口单位和军口单位改变策略的概率增加,双方积极采取PPP模式建设项目,符合演化博弈结果分析。 (3)改变风险分担比例系数和风险成本 保持其他参数不变,将k=0.7调整到k=0.6,得到双方的演化博弈结果如图9、图10所示。通过与图9、图10的比较发现:当民口单位风险分担系数减小即军口单位风险分担系数增大时,双方演化趋势变化不显著。x、y初值较大的曲线均趋于1,初值为0.7的曲线趋势由0趋于1。同理,将s1=3.6调整到s1=2,双方的演化博弈结果如图11、图12所示。通过与图1、图5的比较发现:当风险成本降低后,所有曲线均以较快速度趋于1。 图9 k=0.6时民口单位演化结果 图10 k=0.6时军口单位演化结果 图11 s=2时民口单位演化结果 图12 s=2时军口单位演化结果 结论3:风险成本对博弈稳定策略有负向影响,项目风险分担比例系数对博弈稳定策略影响不显著。PPP项目风险成本大小难以估量。当风险成本降低时,双方的收益才有保障,双方采用PPP模式参与项目的积极性提高。此结论符合演化博弈的推导分析。 通过调整重要参数的大小,对比分析双方采用PPP模式建设项目的演化趋势,可以看出仿真结果与动态演化过程(图2)一致。军民双方是否采取PPP模式,受到军民双方初始意愿、项目收益的正向影响和项目风险成本的负向影响,风险分担比例系数对演化稳定策略影响不显著。项目收益和风险成本参数大小直接影响演化稳定策略的收敛速度和方向,收益与成本之差决定其演化方向。只有军民双方合作收益均大于成本时,双方才会采取PPP模式。 实现军民深度融合,必须走多元化融资道路,兼具融资功能的PPP模式是最有效的措施之一。本文构建了军民双方演化博弈模型,并与SD模型结合来分析演化稳定策略变化过程,结论及对应建议如下: (1)军民双方初始意愿对于军民双方合作有正向影响。军民融合进入发展的关键时期,军口单位采取PPP模式的意愿比以往更强烈,此时应该关注如何提高民口单位参与意愿。首先,国家应该完善顶层设计、军民融合法律法规。其次,地方主管部门应积极落实各项相关政策、及时协调军民纠纷,持续优化PPP模式所处的经济环境、社会环境,营造PPP模式适宜的经营环境。在拥有法律保障和良好经营环境中,军民双方采取PPP模式参与军民融合项目的信心和积极性将大幅提高。 (2)项目收益对于军民双方合作有正向影响,是项目成功的最关键因素之一。基于此,第一,军口单位在考虑项目引进民口单位之前,应做好项目设计、项目可行性研究等工作;第二,民口单位在参与PPP项目前,要充分进行市场调研、慎重考虑PPP运作模式、精细设计盈利模式;第三,采取PPP模式的军民融合项目具有准公共产品的属性,在不影响国家安全和人民生活情况下,各级政府应允许民口单位进行收益调整(如价格调整)。最后,军口单位、地方政府应建立民口单位激励和退出机制,根据民口单位的表现予以经营权、管理方式等权限下放甚至项目收益的让渡,同时将优质PPP项目纳入各级政府PPP项目库。 (3)项目风险对于军民双方合作有负向影响,是项目成败的另一个关键因素。一方面,双方在项目准备阶段做好风险识别工作、在项目实施运营阶段做好沟通协商以降低成本;另一方面,需要成立第三方PPP项目管理公司,协同军口单位加强对民口单位的监管,避免风险失控。(三) 军口单位和民口单位收益矩阵

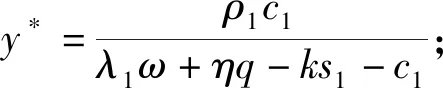




四、演化博弈SD模型及仿真分析
(一) 建立SD模型
(二) SD模型仿真分析
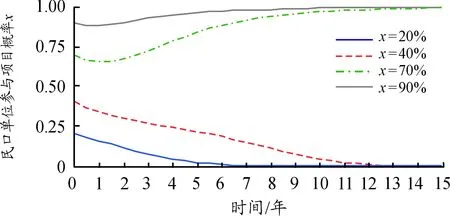
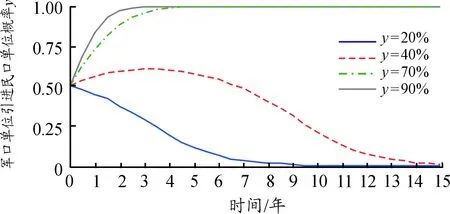
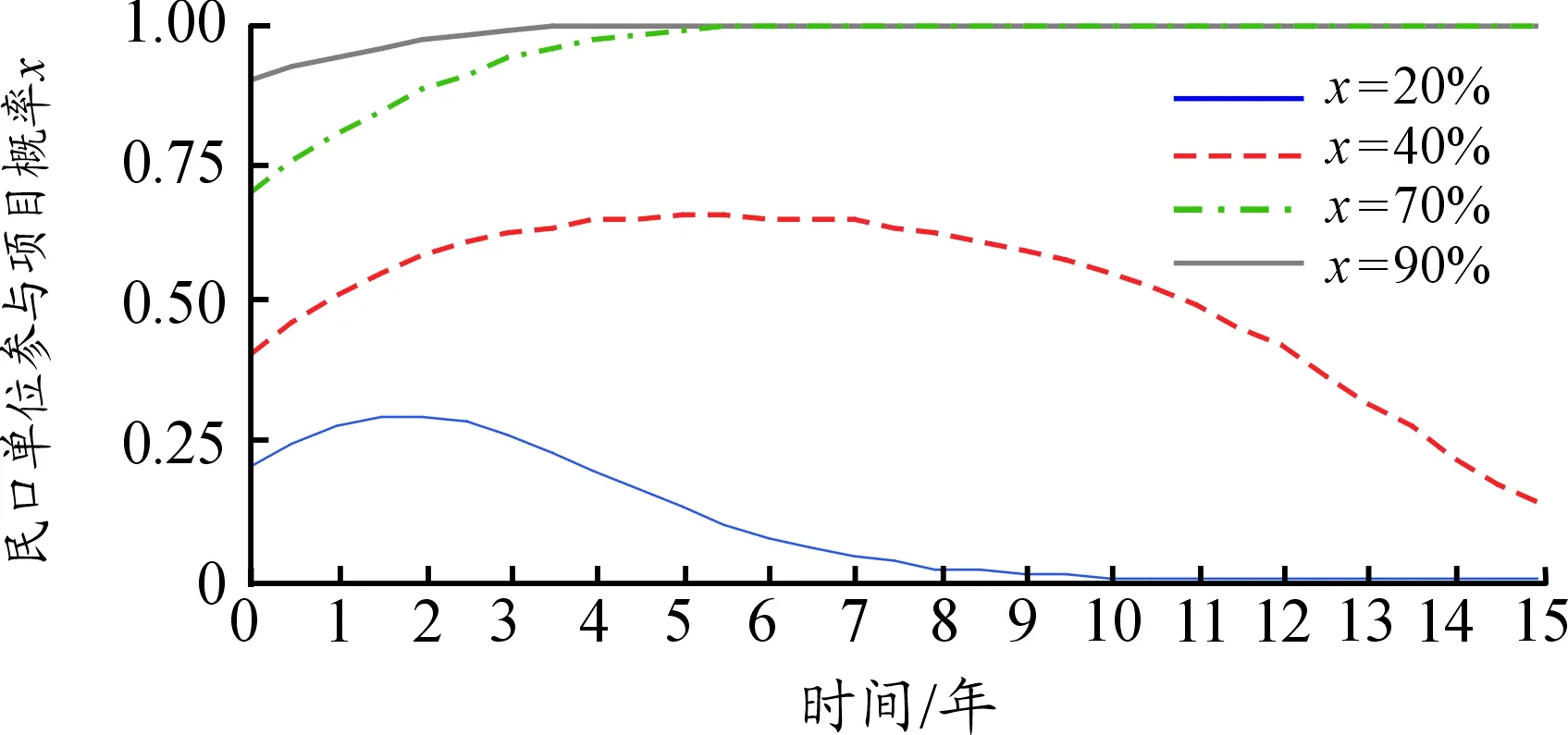

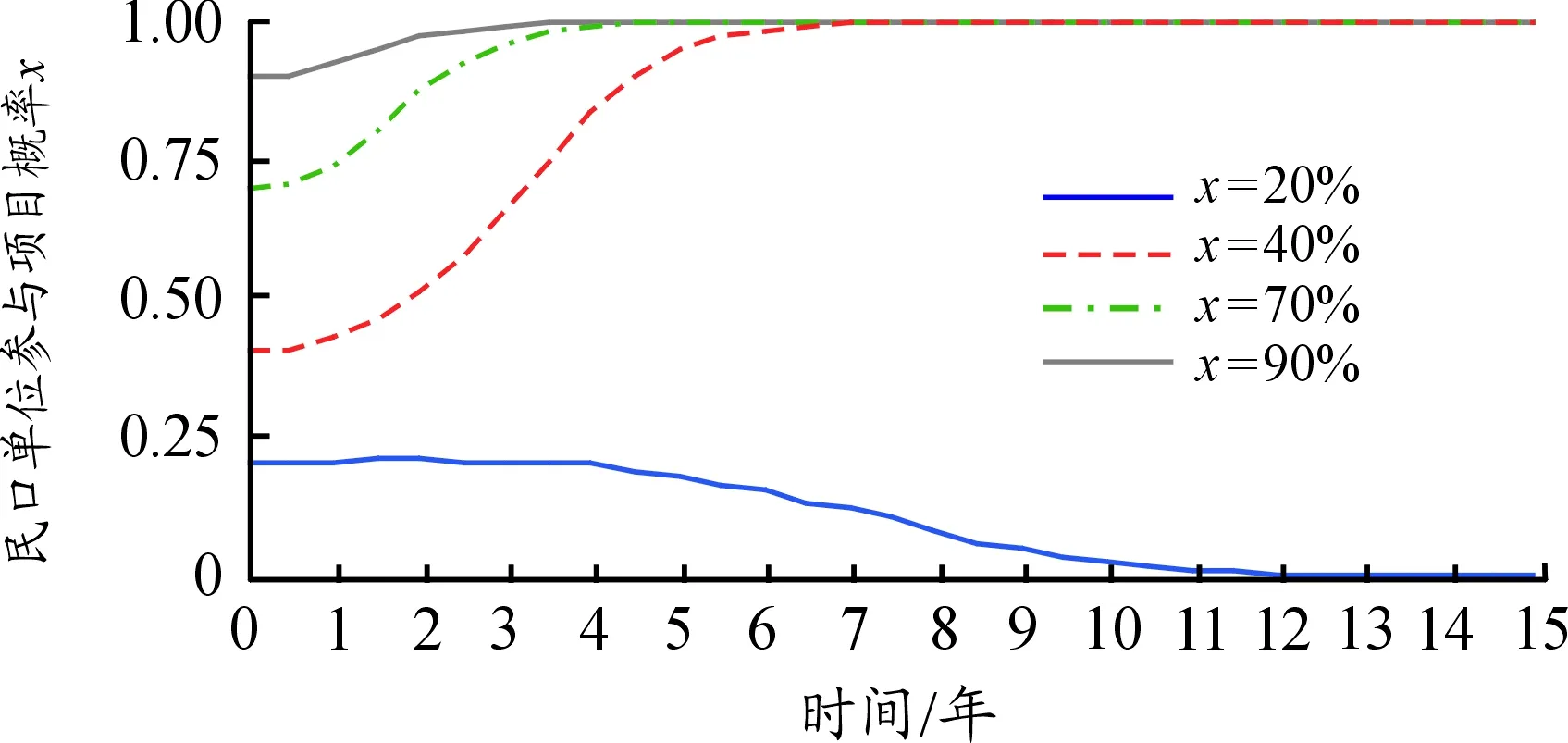
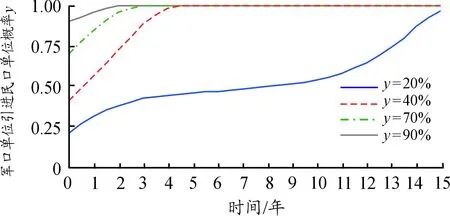
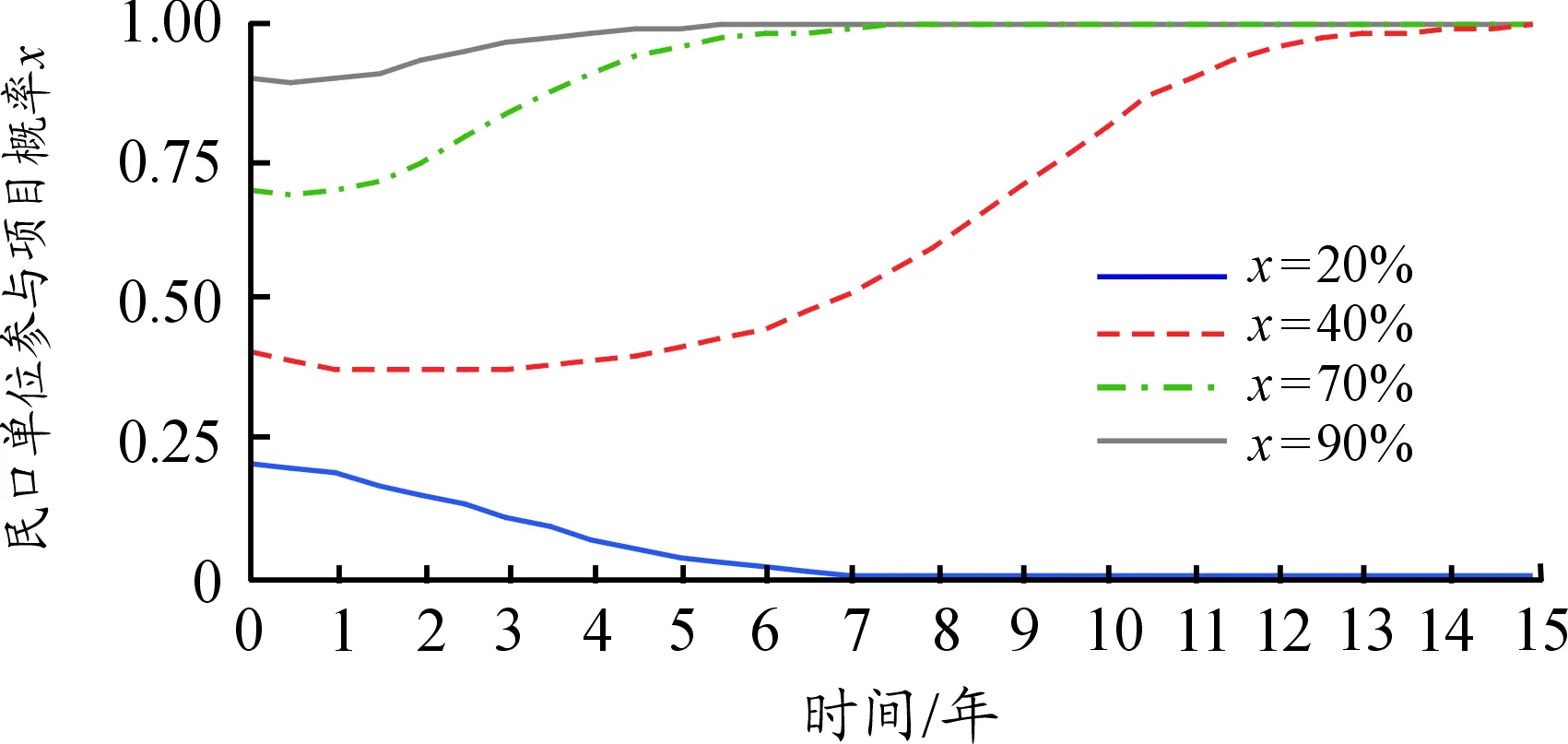
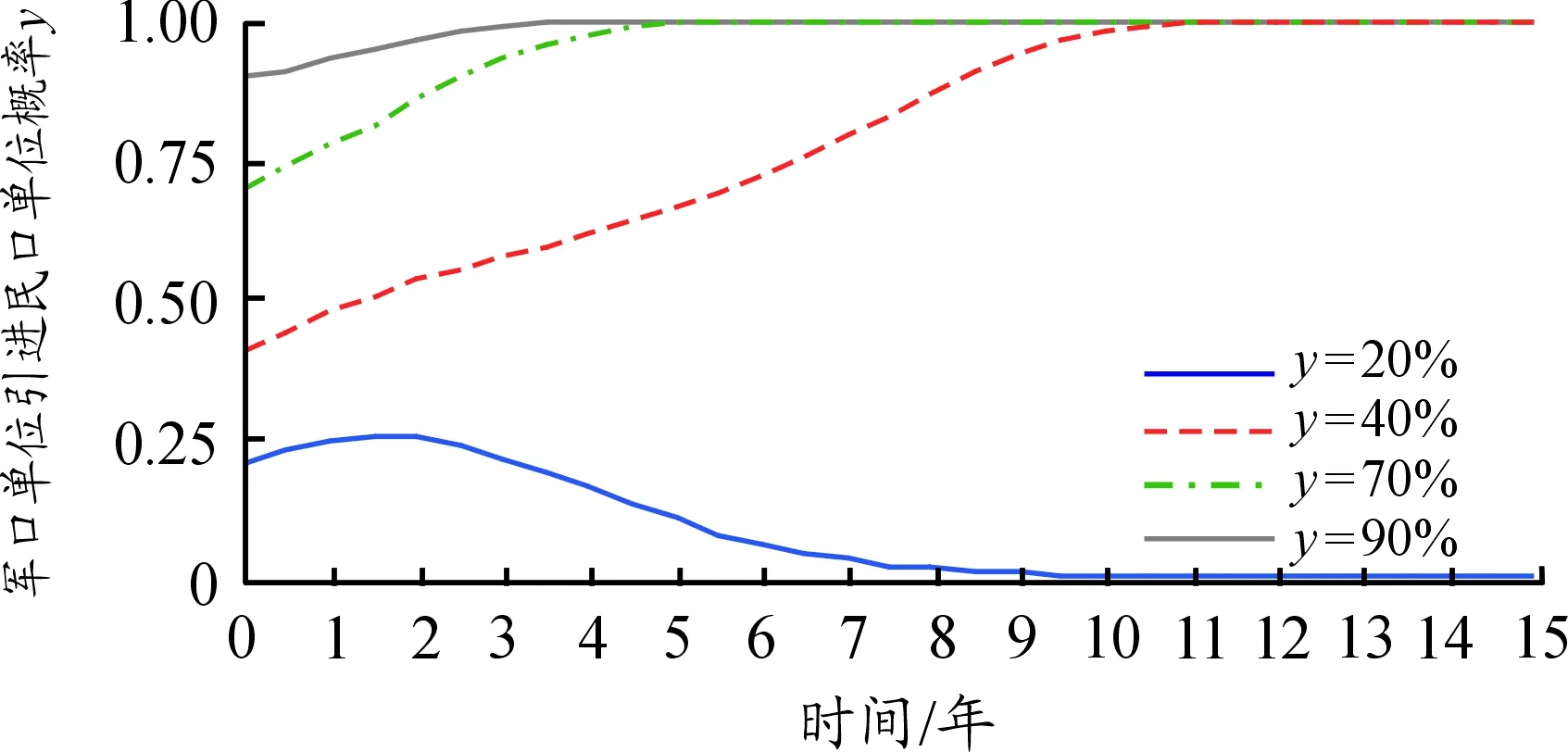
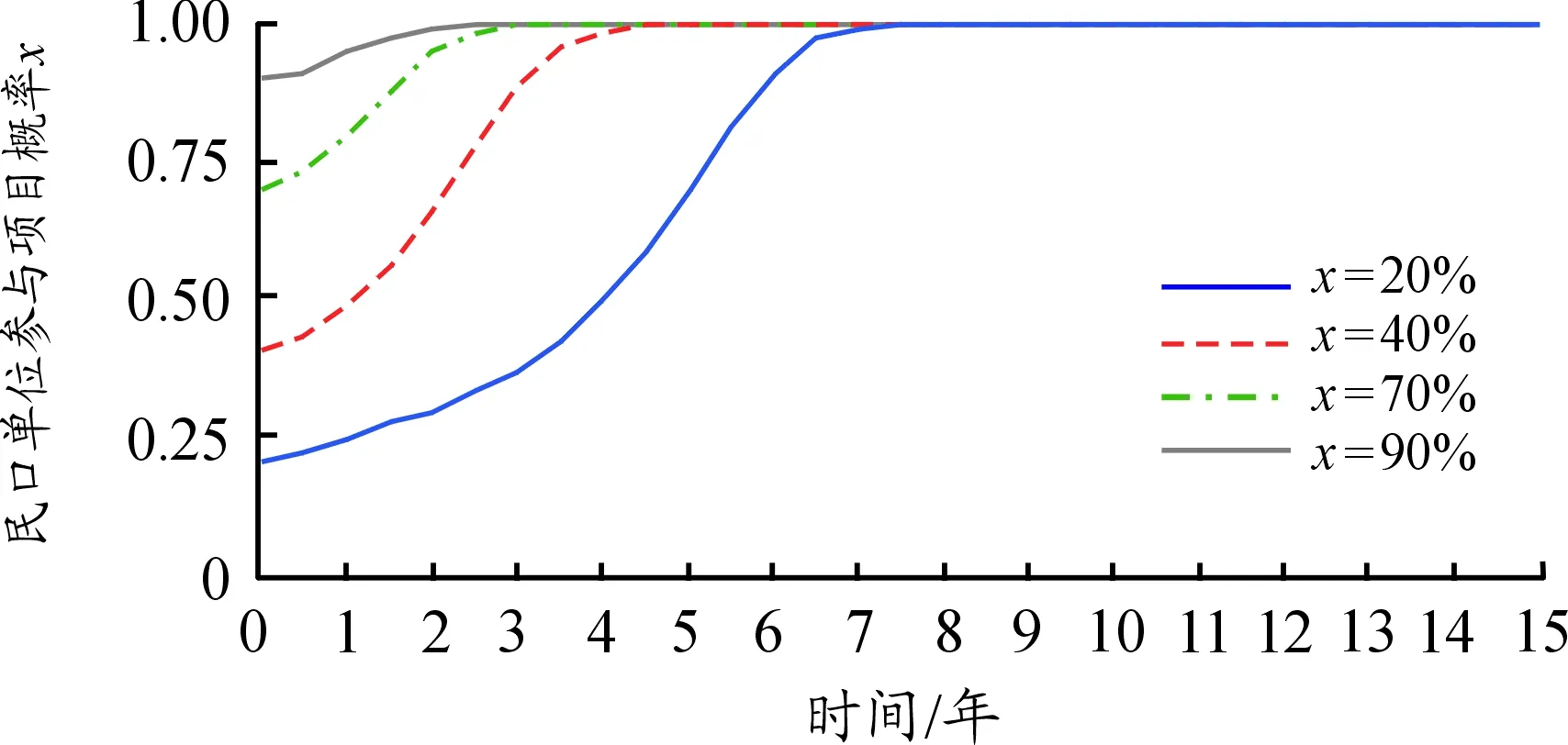

(三) 仿真结果
五、结论与政策建议

