基于准静态法的舱段极限强度研究
黄鎏炜 夏劲松
(1.中国船舶及海洋工程设计研究院 上海200011;2.中国船舶科学研究中心 无锡214082)
引 言
大型船舶长期在海面上航行、工作状态下有极大概率会遇到极端环境,主要由风浪流引起的极限环境会对船体造成极大的损伤,一旦超过船体能承受的最大承载能力,可能对船体以及人员安全造成无法挽回的损失。而极限强度是评判船体能否适应恶劣海洋环境的一个重要指标,因此为了更好地保障船体和人员安全,需要精确评估船舶的极限强度。
随着计算机技术的蓬勃发展,目前,船舶设计的大量计算直接依靠计算机,快速又精准,有限元法也因此发展起来。作为船体极限强度评估的一个重要工具,众多学者使用大型通用有限元软件来计算船舶极限强度,对于船舶强度计算贡献很大。王泽平等[1]运用ABAQUS软件模拟船的舷侧受到撞击的场景,并且对含有液舱围护系统的LNG船进行极限强度分析,得到船体在没有达到极限状态时,围护不会失效的结论。孙斌等[2]以双层底游船搁浅于礁石的场景为背景,通过改进Simth法,提出了针对此场景的船舶受损后极限强度的解析计算预报方法,得出与台礁碰撞不会使船底板发生撕裂,只会发生塑性形变,评估方法准确性较好,对船舶双层底耐撞性结构设计具有一定指导意义。徐海军[3]针对与日俱增的船舶搁浅事故,提出船舶设计应当以安全性为首要因素开展船舶极限强度分析。胡胜谦等[4]基于CRS编制的船体梁极限强度的简化逐步破坏法和有限元法两种方法分析船体极限强度,得出前者更加准确快速地计算出极限弯矩。房长帅等[5]站在质量规范的角度提出要对结构的极限强度作为关键的质量标准。罗文俊和王德禹[6]通过改进AK-MCS方法用来分析船舶极限强度可靠性,能够更加精准地评估船舶在航行过程中局部危险区域的失效概率。张平等[7]针对铝合金悬挂式整体壁板板格长宽比特别大的特点,建立此类板格的非线性有限元模型,进行纵向,横向和剪切载荷作用下的极限强度计算,并与多本规范中板格极限强度的计算公式进行比较,在此基础上提出适用于路和津悬挂式整体壁板板格的极限强度计算公式。
通过长期研究发现,只要模型网格类型网格尺寸合理,材料属性配置正确,并充分考虑影响极限强度的各种因素,都能较准确地计算船体极限强度。[8-9]
本文基于准静态分析(动态显式法)[10]对船体舱段进行非线性有限元分析,比较不同时间步长条件下舱段极限强度变化趋势,研究不同材料模型对舱段极限强度的影响规律,并揭示舱段失效机理,为后期船舶结构极限强度研究提供技术支撑。
1 准静态法简介
准静态法从本质上说是一个结构动态求解的过程。在有限元数值计算过程中,用中心差分的方法对运动方程进行显式时间积分,应用一个增量步的动力学条件计算下一个增量步的动力学条件。当增量步开始时(t时刻),计算加速度为:
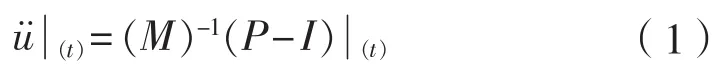
然后对加速度在时间上采用中心差分进行积分,在计算速度的变化时假定加速度为常数。应用这个速度的变化值加上前一个增量步中点的速度来确定当前增量步中点的速度:

速度对时间的积分加上在增量步开始时的位移以确定增量步结束时的位移:

准静态法采用中心差分法进行显式时间积分不存在收敛性问题,能够很好地求解复杂结构崩溃问题。图 1为基于准静态法开展非线性有限元计算的流程图。

图1 基于准静态法的非线性有限元计算流程
2 舱段模型范围
船体舱段结构为2层甲板、单底,舱段总长3.40 m、总宽约3.26 m、型深约2.40 m。图 2为舱段结构图,图 3为舱段结构板厚示意图。
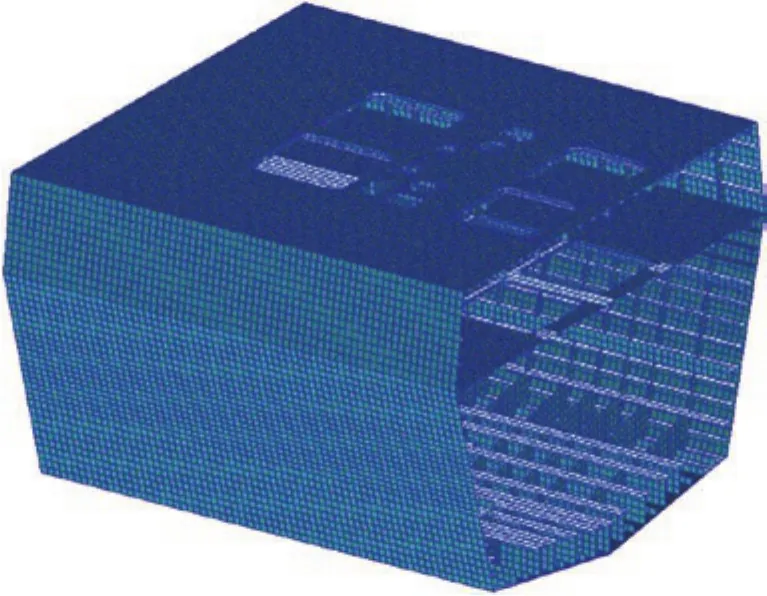
图2 舱段结构图

图3 舱段结构板厚示意图
3 边界条件及载荷施加
本次数值仿真计算中坐标系定义为:x轴沿船长方向,指向艏部为正;y轴沿船宽方向,指向左舷为正;z轴沿型深方向,向上为正,坐标原点在125号。
模型两端建立相应的独立点,采用多点约束进行边界条件的定义,边界条件为一端释放y向转角和x向位移,其他方向固定,如图 4所示。根据此边界条件,在两端的y方向分别施加转角位移,由于本船静水中为中垂状态,在波浪中航行时,其中垂状态较为危险,因此施加转角位移使其产生中垂状态,研究该状态下的极限承载能力。

图4 数值仿真中多点约束边界
4 极限强度数值仿真
图 5给出了舱段的极限强度数值仿真等效应力应变关系,图 6给出了舱段的极限强度数值仿真弯矩-曲率曲线。

图5 数值仿真中等效应力应变关系
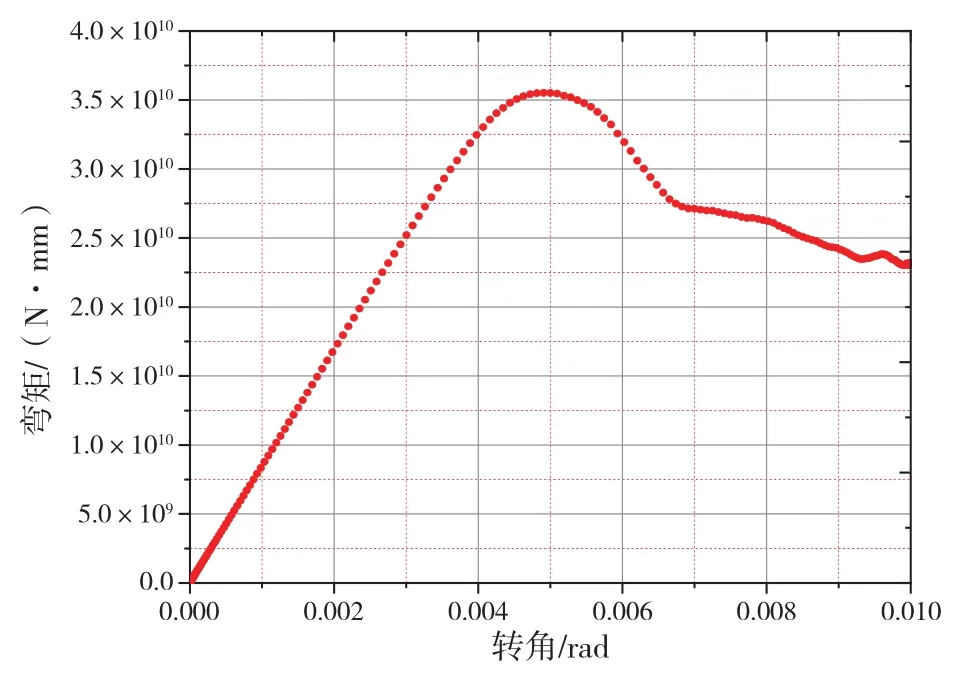
图6 舱段弯矩-曲率曲线
通过图 6可以看出,当弯矩达到极限前,弯矩曲率基本为线性状态,当舱段的极限弯矩达到3.55×1010N·mm时,转角位0.004 9 rad(极限状态);随着转角的增大,弯矩下降。
图 7和图 8给出了01甲板和1甲板的应力云图。
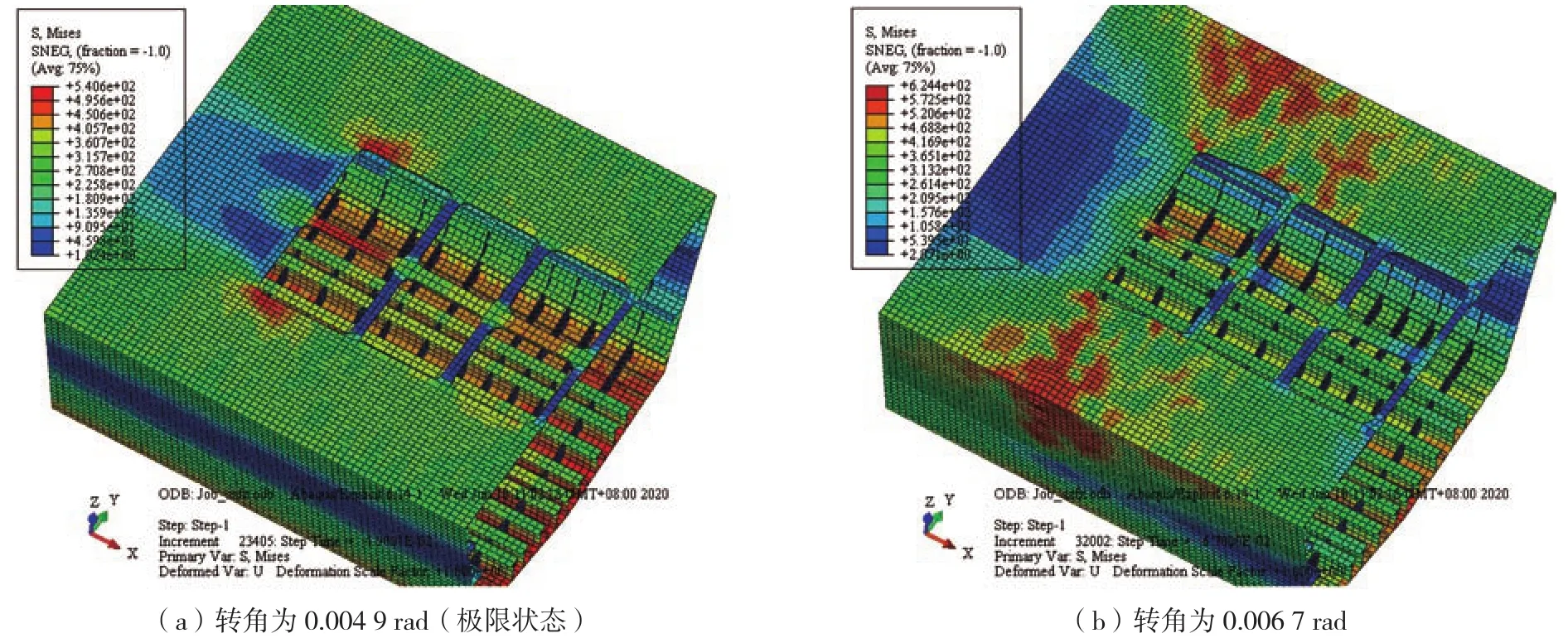
图8 1甲板应力云图
通过图 7可以看出:当载荷达到极限状态时,01甲板的边板、开口边板(船舯)和舷侧列板已经发生塑性变形,达到了屈服极限;当转角为0.006 7 rad时,01甲板的边板、开口边板(船舯)和舷侧列板已经发生失效变形。
通过图 8可以看出:极限状态下1甲板开口角隅区域、开口边板(船舯)发生了局部屈服;当转角达到0.006 7 rad时,1甲板的边板、开口边板(船舯)和舷侧列板已发生塑性变形。
5 时间步长对极限承载能力的影响
本节分析不同的时间步长对舱段模型极限强度的影响分析,下页图9为不同时间步长下的弯矩-曲率曲线。由图 9可知:当时间步长为0.05时,极限弯矩为2.91×1010N·mm;当时间步长为0.10时,极限弯矩为2.79×1010N·mm;当时间步长为0.15时,极限弯矩为2.74×1010N·mm;当时间步长为0.20时,极限弯矩为2.71×1010N·mm;当时间步长为0.25时,极限弯矩为2.69×1010N·mm。
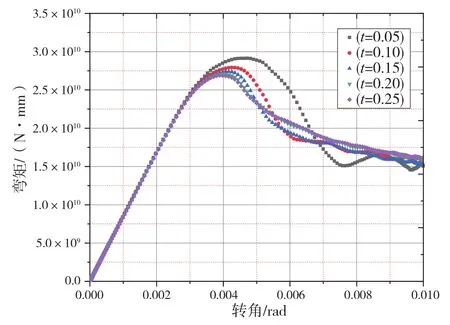
图9 不同时间步长下的弯矩-曲率曲线
随着时间步长的增加,极限强度值越来越小,但趋于稳定;在线弹性阶段,弯矩曲率曲线完全一致。由线弹性阶段结束致极限状态,弯矩值随着时间步长的增加而减小;由极限状态致后屈曲状态,弯矩值随着时间步长的增加而增大。
6 材料模型对极限承载能力的影响
本节主要进行了材料模型对舱段模型极限强度和舱段失效模式的影响分析。主要包括以下3种材料模型:
(1)屈服强度为390 MPa的理想弹塑性模型;
(2)屈服强度为540 MPa的理想弹塑性模型;
(3)屈服强度为528 MPa的简化材料模型。
材料模型见图 10,图 11给出了3种材料模型下的弯矩-曲率曲线。
通过计算得出,屈服极限为390 MPa理想弹塑性材料的极限弯矩为2.79×1010N·mm;屈服极限为540 MPa理想弹塑性材料的极限弯矩为3.54×1010N·mm;屈服极限为528 MPa简化材料的极限弯矩为3.51×1010N·mm。通过对比可以看出:对于理想弹塑性材料,随着屈服极限的增大,极限弯矩增大。
下页图 12给出了屈服极限为390 MPa理想弹塑性舱段模型失效过程。

图10 材料的本构模型
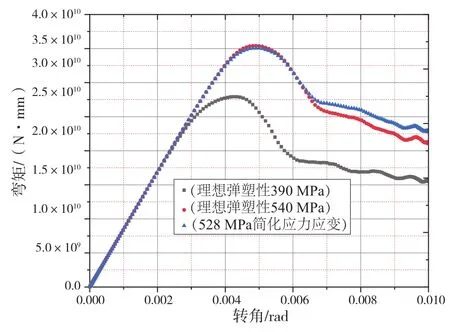
图11 3种材料模型下的弯矩-曲率曲线
当载荷达到1.38×1010N·mm时,01甲板开口角隅开始屈服,见图12(a);当载荷达到1.73×1010N·mm时,01甲板中纵桁屈服,见图12(b);当载荷达到2.27×1010N·mm时,01甲板板架屈服,见图12(c);当载荷达到2.39×1010N·mm时,01甲板舷顶列板开始屈服,见图12(d);当载荷达到2.49×1010N·mm时,1甲板角隅开始屈服,见图 12(e); 当载荷达到 2.79×1010N·mm 时,整体结构形成塑性铰,达到了舱段的极限状态,见图12(f);1甲板板架屈服,见图12(g);01甲板和1甲板舷侧结构发生侧倾失效,见图12(h);整个舱段结构的失效模式,见图12(i)。
下页图 13给出了屈服极限为540 MPa理想弹塑性舱段模型失效过程。

图12 理想弹塑性(屈服极限390 MPa)

图13 理想弹塑性(屈服极限540 MPa)
当载荷达到1.92×1010N·mm时,01甲板开口角隅开始屈服,见图13(a);当载荷达到2.39×1010N·mm时,01甲板中纵桁屈服,见图13(b);当载荷达到3.13×1010N·mm时,01甲板板架屈服,见图13(c);当载荷达到3.3×1010N·mm时,01甲板舷顶列板开始屈服,见图13(d);当载荷达到3.4×1010N·mm时,1甲板角隅开始屈服,见图13(e);当载荷达到3.54×1010N·mm时,整体结构形成塑性铰,达到了舱段的极限状态,见图13(f);1甲板板架屈服,见图13(g);01甲板和1甲板舷侧结构发生侧倾失效,见图13(h);整个舱段结构的失效模式,见图13(i)。
图 14给出了简化真实材料(屈服极限528 MPa)情况下的舱段模型失效过程。
我国自20世纪70年代开始对图书馆自动化系统进行研究,主要是对国外引进的系统进行研究与改进,在随后的几十年间,紧跟国外最新发展趋势。陈伟(2005)在《国内外图书馆自动化系统发展现状与趋势》一文中提到,尽管国内图书馆集成管理系统在开发与研究上获得了不小的进展,但由于技术与规模的限制,在功能上仍与国外图书馆集成管理系统有一定的差距[11]。而对于国外的产品,贾西兰等(2016)在 《“互联网+图书馆”思维下的下一代图书馆服务平台》中指出,虽然国外图书馆集成管理系统已经相对成熟,但无法满足我国图书馆特有的本地化需求,对于中国用户来说还有很多的地方需要改进、拓展、完善、汉化[12]。
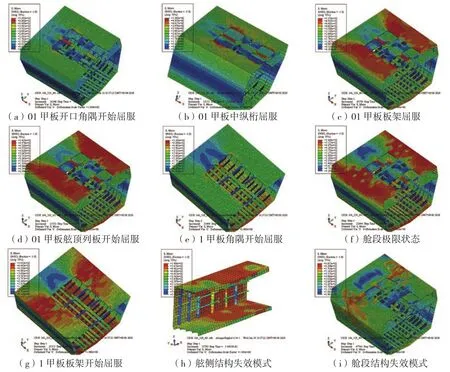
图14 简化真实材料(屈服极限528 MPa)
当载荷达到1.86×1010N·mm时,01甲板开口角隅开始屈服,见图14(a);当载荷达到2.38×1010N·mm时,01甲板中纵桁屈服,见图14(b);当载荷达到3.14×1010N·mm时,01甲板板架屈服,见图14(c);当载荷达到3.29×1010N·mm时,01甲板舷顶列板开始屈服,见图14(d);当载荷达到3.34×1010N·mm时,1甲板角隅开始屈服,见图 14(e); 当载荷达到 3.51×1010N·mm 时,整体结构形成塑性铰,达到了舱段的极限状态,见图14(f);1甲板板架屈服,见图14(g);01甲板和1甲板舷侧结构发生侧倾失效,见图14(h);整个舱段结构的失效模式,见图14(i)。
通过上述的分析可以看出,极限弯矩随着屈服极限的增大而增大。通过第39页图 11可以看出:对于屈服极限为540 MPa的理想弹塑性,以及屈服极限为528 MPa、根据真实材料曲线简化得到的应力应变曲线的舱段模型而言,两者的极限弯矩基本相同,且弹性阶段和塑性阶段变化趋势基本一致。
通过对比屈服极限为390 MPa和540 MPa的理想弹塑性材料模型计算结果可以看出,对于屈服极限为390 MPa的失效顺序是:01甲板开口角隅开始屈服甲板中纵桁屈服甲板板架屈服(2.27×甲板舷顶列板开始屈服(2.39×甲板角隅开始屈服(2.49×1010N·mm)舱段极限状态(2.79×1010N·mm);对于屈服极限为540 MPa的失效顺序是:01甲板开口角隅开始屈服甲板中纵桁屈服(2.39×甲板板架屈服(3.14×1010N·mm)甲板舷顶列板开始屈服1甲板角隅开始屈服舱段极限状态(3.54×1010N·mm)。
对于屈服极限为528 MPa根据真实材料曲线简化得到的应力应变曲线的舱段模型失效顺序是:01甲板开口角隅开始屈服甲板中纵桁屈服甲板板架屈服甲板舷顶列板开始屈服甲板角隅开始屈服舱段极限状态(3.51×1010N·mm)。
通过对比可以发现3种材料的失效模式和顺序一致。
7 结 论
本文基于准静态法(动态显示法)对船体舱段进行了非线性有限元分析,比较不同时间步长条件下舱段极限强度变化趋势,研究了不同材料模型对舱段极限强度的影响规律,并揭示了舱段失效机理,主要得出以下几点结论:
(1)通过数值仿真计算发现,由于舱段极限状态下失效主要发生在开口区域,属于该跨范围内的失效;
(2)在线弹性阶段,弯矩曲率曲线完全一致。由线弹性阶段结束致极限状态,弯矩值随着时间步长的增加而减小;由极限状态致后屈曲状态, 弯矩值随着时间步长的增加而增大。
(3)通过计算分析,给出了不同屈服极限下的理想弹塑性材料模型的失效模式以及极限弯矩,同时对比分析了相同屈服极限下的理想弹塑性模型和真实材料简化得到的材料模型的失效模式及极限弯矩,且失效顺序一致。

