三次函数引思考 回归教材探本源
周翔 郑传远

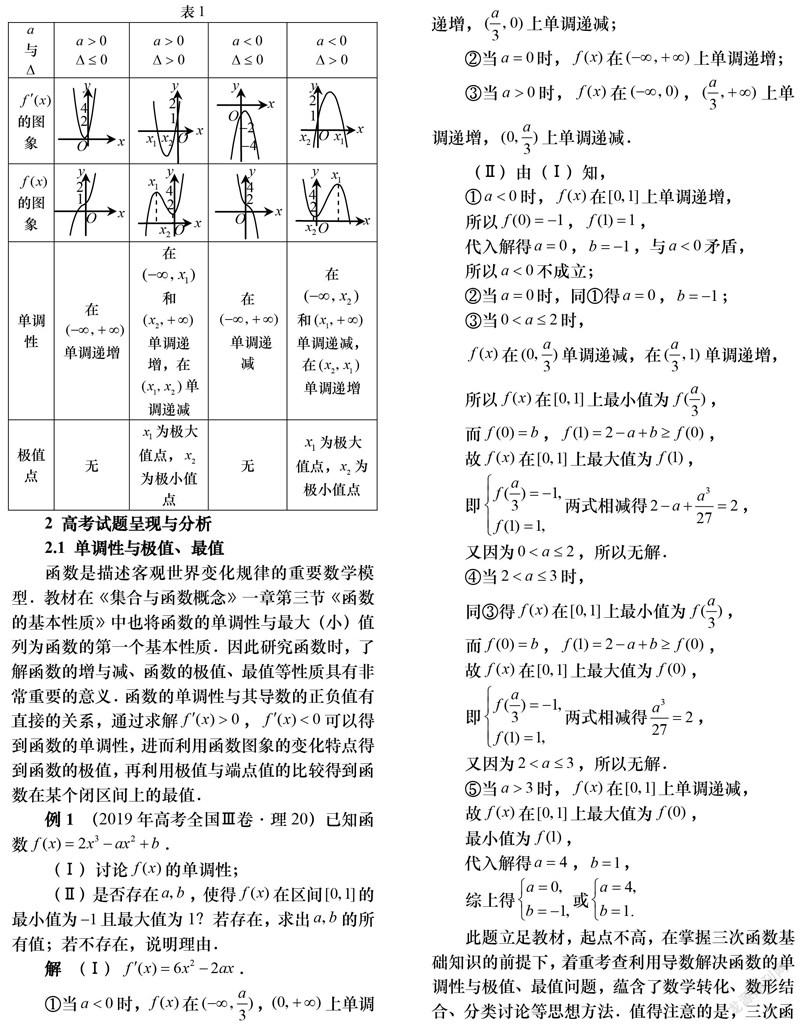

三次函数是高中数学重要的函数模型,频繁见于选修2-2《导数及其应用》,无论在例题教学,还是课后习题,都出现大量以三次函数模型为载体的问题.回顾高考,三次函数模型已经连续两年出现在导数解答题中.显然,三次函数已经成为高考命题的一个热点和亮点.本文从教材的一道课后习题出发,追根溯源,就利用导数研究三次函数问题的特点做出分析,并在此基礎上给出教学建议.
导数题中不等式证明问题通常都是综合利用导数研究极值、最值结论和不等式的放缩结果,在证明过程中,可以适当地使用证明的分析法、综合法、反证法等,对学生的综合能力要求较高,特别是数学运算和逻辑推理能力,同时还需要有较强的创新意识.此类考题具有良好的选拔功能.
3若干教学启示
3.1回归教材:实基础
导数的应用是高中数学的核心内容之一,也是高考的重点与热点.从近几年高考试题来看,以三次函数模型为载体的导数解答题出现的频率越来越高,由于此类问题在教材中有相应的原型,这就要求我们在平时的教学中应注重回归教材,夯实基础,跳出题海战术,回归学科内涵,而非一味地好高骛远.
3.2关注本质,把握规律
回归数学本质是高考命题的必然趋势,因此,关注数学本质应是教学上的重中之重.关注知识的本质特征,关注知识间的内在联系,关注公式定理的形成过程,应成为教学过程中的核心内容.通过对近几年高考试题的分析可以发现,导数的应用立足于教材,着重考查利用导数解决函数的单调性与极值、最值、零点、恒成立、不等式证明等问题,蕴含了转化与化归、分类讨论、数形结合、函数与方程等思想方法.看起来花样繁多,但万变不离其宗,如果能从基本的数学模型入手,深刻理解其图象的特征及基本性质,再借助于数学思想方法,就可以轻易破解此类问题.
3.3落实课堂,培育素养
导数的应用问题常出现在试卷的压轴位置,主要考查学生的运算与逻辑推理能力.在实际教学过程中,教师往往更加关注与指数、对数有关的导数问题,却忽略了一些更为常见或简单的函数模型.而近几年的高考题,反复出现了利用导数研究三次函数的问题,因此,教师在教学过程中,要避免过度变式,应更注重教材内容的深层挖掘,强调知识的应用,鼓励学生勤动手、勤反思,多运算、多思考,培育学生的直观想象、逻辑推理、数学运算等数学学科核心素养.
总之,利用导数研究三次函数的高考试题,依据学业质量标准和课程内容,以素养为落脚点,考查学生对基础知识和基本方法的掌握程度,考查学生对重要数学思想方法的理解程度,考查学生在日常学习中数学活动经验的积累程度,对教学发挥了正确的导向作用.

