光学超分辨平面超构透镜研究进展
周 毅,梁高峰,温中泉,张智海,尚正国,陈 刚
光学超分辨平面超构透镜研究进展
周 毅1,2*,梁高峰1,2,温中泉1,2,张智海1,2,尚正国1,2,陈 刚1,2
1重庆大学光电工程学院,重庆 400044;2重庆大学光电技术及系统教育部重点实验室,重庆 400044
从光学自身机理上突破光学理论分辨率极限,实现远场超分辨光学点扩散函数,进而实现超分辨聚焦和超分辨成像,在激光加工、超分辨光学显微和超分辨望远等系统有着重要应用前景。近年来,光学超构表面的发展使得在亚波长尺度上实现光场振幅、相位及偏振的独立调控成为可能,为研制新型的超分辨平面超构透镜提供了更加灵活的手段。本文介绍了基于光学超构表面的超分辨平面超构透镜、相关测试技术方面几年来的研究进展,并讨论了该领域面临的问题和未来的研究重点和方向。
光学超分辨;超振荡;平面透镜;超构表面
1 引 言
由于衍射效应限制,传统光学系统无法突破分辨率理论极限0.5/(为波长,NA为数值孔径)[1]。超分辨光学成像技术的突破将引领光学显微、光学遥感、深亚波长光刻、超高密度数据存储等军民相关领域的技术革命,具有重大的科学意义和应用价值。如何突破衍射极限制约,实现超分辨光学成像已成为光学领域的重要研究课题[2]。近年来,已发展出了多种超分辨光学显微技术。受激发射损耗荧光显微技术[3],可实现1 nm的单荧光分子定位精度,其不足是需要荧光标记和图像重建;基于结构光照明的超分辨显微技术可实现/5空间分辨率[4],然而其需要附加特殊光照明和图像重建;近场光学显微技术[5]通过检测样品表面倏逝波,实现超分辨率光学成像;基于表面等离子激元的近场聚焦透镜可实现22 nm空间分辨率[6],但近场成像仅局限于样品表面;负折射率超构透镜已有实验验证,但其加工难、光损耗大,无法实现远场成像[7]。如何实现无需图像后续处理的无标记远场超分辨光学成像是光学研究领域的重大挑战,亟待开展基于新原理、新结构、突破衍射极限的远场成像器件相关基础理论和关键技术研究。基于亚波长结构波前调控的新型远场微透镜已有报道,但其设计仍基于传统透镜相位分布[8-10]和光线汇聚原理[11],无法突破衍射极限。光学超振荡是一种利用空间频率较低的平面波,实现局域空间快速振荡的特殊光学现象[12]。以式(1)为例,函数()由max个谐波叠加而成,第个谐波的频率为0、复振幅为a,最高谐波频率为max0。通过选择适当的复振幅,()的局部振荡(实线)可远快于最高频率谐波(虚线),如图1所示。原则上超振荡场的分辨率没有理论极限[13],这为突破衍射极限的远场超分辨聚焦/成像提供了崭新的途径。

2 亚波长光场调控
光场调控通常是指对光波电矢量的振幅、相位和偏振等进行调控。早期的超分辨透镜通常采用简单的二值振幅和二值相位调控方式对入射光场进行调控,以实现出射光场特定的相干叠加,形成超振荡光场。这种调控方式比较简单,对于器件加工也相对容易,然而这极大地降低了器件对光场的调控能力,进而制约了超分辨透镜的性能(如效率、旁瓣抑制等)[13-14]。近年来,光学超构表面的发展,为在亚波长尺度对光场的振幅、相位及偏振调控提供了有效的手段[15‒20]。相对于金属超构表面,全介质超构表面具有振幅透射率高等特点[21-22],这对于聚焦效率本身相对较低的超分辨透镜极其重要。对于全介质超构表面,通常折射率越大,其效率就会越高,同时高折射率材料还有利于降低超构表面器件的加工深宽比,降低加工难度。因此,针对不同的光学波段,通常采用折射率大、消光系数小的介质作为超构表面的结构材料。例如在550 nm以下的短波长,可以选用TiO2[23],其折射率可达到2.5;而在550 nm以上的光波段,可以采用-Si[24],其折射率高达3.0;而在红外波段和太赫兹波段,可以选择Si[25‒28],其折射率达到了3.4。对于相位调控最常使用的是几何相位超构表面,其本质上是一个亚波长尺度的半波片,基本形貌可以是立方形或是椭圆柱形。通过优化其长、宽和高,可以使光波在沿长和宽两个偏振方向的相位差为π,同时使两种偏振的振幅透射率一致,进而形成一个亚波长尺度的半波片超构表面单元结构。当入射光波为圆偏振光时,出射光场通常包含与入射圆偏振正交的交叉圆偏振态及与入射光波相同的圆偏振态。当半波片超构表面单元结构的性能越接近理想半波片时,未被调制的入射光含量越小,在理想情况下出射光场只包含交叉圆偏振光场。当旋转几何相位超构表面单元结构时,出射的交叉圆偏振态的附加相位是旋转角度的两倍。利用这一特性,可实现对入射圆偏振光0~2π的连续相位调控。全介质超构表面,不但能够控制出射光场的相位,而且可以用于偏振态的控制[29-30]。在线偏振光入射条件下,可以利用半波片的性质,通过旋转半波片超构表面单元结构,使得出射线偏振射光的偏振方向发生旋转,从而在亚波长尺度下,实现空间局部任意偏振方向的控制,由此用于矢量光场(角向偏振和径向偏振等)的产生。除了半波片外,类似地,还可以构建具有四分之一波片性能的超构表面[31],在圆偏振光入射条件下,可以通过旋转四分之一波片实现出射线偏振方向的控制。进一步,可以通过优化设计多个具有不同初始相位的四分之一波片或二分之一波片,让其初始相位涵盖0~2π范围,则可以实现相位和偏振两者的同时独立调控[32]。未来超构表面将进一步向多维度光场操控发展[33]。
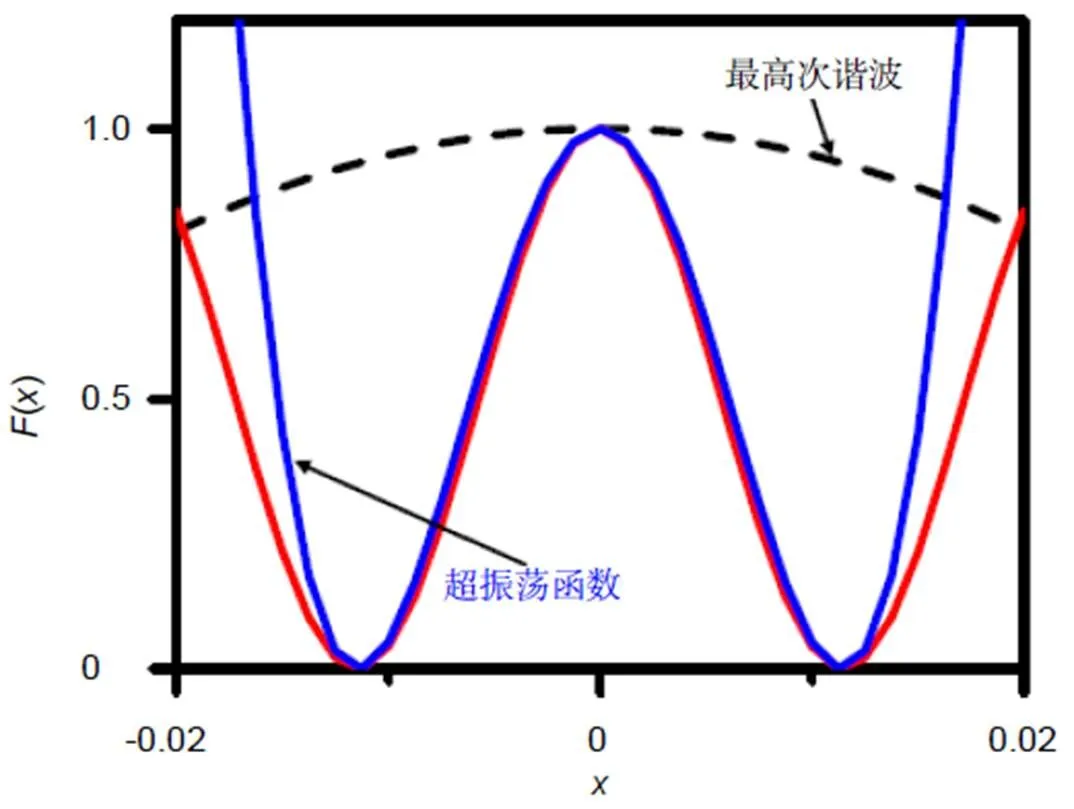
图1 超振荡函数示意图。一个采用Nmax个谐波构建的超振荡函数, 在空间局部位置其空间变化远远高于最高次谐波[12]
3 标量超分辨平面超构透镜
常见标量光场包括线偏振光场、圆偏振光场和椭圆偏振光场,在这类光场聚焦形成焦斑中心位置,偏振方向通常与入射偏振态相同。而在偏离中心的位置,通常包含有与传播方向一致的纵向偏振分量。当透镜数值孔径较小时,通常这种纵向偏振分量较小而可以忽略。当透镜数值孔径较大时,这一分量的存在将会导致整体聚焦光斑光场尺寸的扩大。然而,在很多实际应用场合,例如光学显微、望远系统,由于放大导致的光杠杆效应[34],这一分量不会出现在系统最终形成的成像光场内。因此,在研究标量超分辨平面超构透镜的时候,通常只考虑聚焦光场中的横向偏振分量。普通的标量超分辨平面超构透镜已有大量报道[35‒41],以下我们仅重点针对标量超分辨平面超构透镜色差和轴外像差矫正进行介绍。
3.1 消色差超分辨平面超构透镜
超构表面透镜作为一种衍射光学器件,与其它衍射透镜一样,其自身也存在着严重的色差。尽管这类透镜能够工作在较宽的光学波段,然而色差的存在严重制约了其在光学聚焦和成像当中的应用。特别是对于光学超分辨平面超构透镜,如何在实现超分辨点光学扩散的同时,消除平面超构透镜的色差还面临着诸多挑战。
3.1.1 多波长消色差超分辨平面超构透镜
类似于传统的消色差透镜,在若干个离散分布的波长上实现色差的矫正,相对而言比较容易实现。因此,早期报道的消色差超分辨平面超构透镜大多针对多个波长进行色差矫正。
2017年,新加坡南洋理工大学和英国南安普顿大学联合公开报道了一种三色消色差超分辨平面超构透镜[42],该透镜设计基于二值振幅调控,透镜半径为20 µm,焦距为10 µm,对应的数值孔径和衍射极限分别为=0.894和FWHMDL=0.559(0.5/)。针对每个波长满足的光场分布目标函数,通过多目标粒子群优化算法[43]进行多波长消色差优化设计。利用金属环带结构(金属环带振幅透射率为0,无金属的环带透射率为1),实现对入射光场二值振幅调控。实验表明,在可见光波段实现了R=405 nm、G=532 nm和B=633 nm三个波长的消色差超分辨聚焦。在共同的焦距位置处,均形成了横向尺寸小于传统光学衍射极限的超分辨聚焦光场。其三个波长焦斑尺寸分别为0.457R、0.445G和0.54B。与传统消色差透镜不同,除了在焦平面位置存在明显的聚焦光斑外,该透镜在光轴上其他位置也存在明显的焦斑。这是因为在其优化设计中并未能对轴向光场分布进行约束。该文献还报道了近红外波段的2波长消色差超分辨平面透镜。利用该方法,还可以实现4个波长的多波长消色差超分辨平面超构透镜设计。由于仅仅采用二值振幅进行超分辨平面透镜设计,其设计自由度低,极大地限制了多波长消色差性能,同时也会降低超分辨聚焦的效率。
采用几何相位超构表面,通过旋转可以实现对交叉正交圆偏振光场0~2π的连续相位调控。几何相位与入射波长无关,常应用于宽带平面超构透镜设计。2019年湖南大学报道了一种基于几何相位超构表面的多波长消色差超分辨平面超构透镜理论设计和仿真结果[44]。透镜半径为10 µm,焦距为10 µm,对应的数值孔径和衍射极限分别为=0.707和FWHMDL= 0.707。针对473 nm、532 nm和632.8 nm等3个波长,对TiO2几何超构表面进行优化设计,振幅透射率大于0.823。类似地,采用多目标优化模型对器件进行优化设计。通过对比二值相位(0和π)调控和4值相位(0、π/2、π和3π/2)调控,发现随着相位调控的自由度增加,在实现消色差的基础上,可以进一步实现焦平面超分辨聚焦光场横向尺寸的压缩,并有效地提高了消色差超分辨平场超构透镜的聚焦效率。其焦斑横向尺寸达到0.510、0.530和0.499,而聚焦效率在532 nm和632.8 nm两个波长处,相对于二值相位调控提高了约2倍。

图2 全介质超构表面。(a) TiO2几何相位超构表面[23];(b) Si半波片超构表面[30];(c) SiNx四分之一波片超 构表面。采用不同尺寸的四分之一波片超构表面覆盖0~2π相位范围,实现独立的相位调控和偏振调控[32]
2020年,该研究组进一步提出了一种基于连续相位调控的消色差超分辨平面透镜设计方法[45]。所提出的透镜相位分布由三部分组成,包括一个连续变换的传统平面超构透镜相位、一个二值相位模板和一个色散项。通过优化设计,使TiO2超构表面单元结构满足特定的色散关系。并通过粒子群优化算法,针对492 nm、512 nm、532 nm、552 nm、572 nm和592 nm等6个独立波长,对该相位模板和透镜色散项进行优化,最终实现多波长消色差超分辨平面超构透镜设计。该透镜半径和焦距分别为15 µm和100 µm,对应的数值孔径和衍射极限分别为=0.148和FWHMDL=3.37。理论仿真表明,在焦平面上焦斑横向尺寸分别为衍射极限的0.794、0.796、0.799、0.780、0.815和0.788倍。进一步的仿真表明,除了在设计波长处,该透镜在482 nm~592 nm约110 nm的带宽范围内的其他4个波长,也能够实现消色差超分辨聚焦。然而,受限于超构表面单元结构的色散能力,该方法难以实现大数值孔径的消色差超分辨平面超构透镜。2020年,中国科学院光电技术研究所基于类似方法[46],实现了多波长消色差超分辨平面透镜,并通过理论仿真验证了其超分辨成像功能。
2021年,重庆大学报道了一种基于光全息的多波长消色差超分辨平面超构透镜设计方法[47]。针对个独立波长λ(=1,…,),利用粒子群优化算法,分别设计个具有共同焦距的超分辨透镜,其对应的复振幅透射函数为T(,,;λ)。利用全息原理,将这个透镜融合到一个总的相位分布中,得到消色差超分辨透镜的复振幅透射率(,,)=∑cT(,,;λ),并进一步通过粒子群优化算法,对权重系数c进行优化,确保焦平面的聚焦光斑强度最大。针对520 nm、555 nm、632.8 nm、660 nm和690 nm,分别基于32值(2π/32,=0,…,31)相位调控,独立设计6个半径为42.7 µm,且具有相同焦距=12.7 µm的超分辨透镜,对应的数值孔径高达=0.96。利用上述方法进一步优化设计,同时为了便于实验实现,对复振幅进行了振幅二值化处理,最后完成了消色差超分辨平面透镜的设计和制备,并在实验上获得的焦斑横向尺寸分别为0.458、0.419、0.408、0.43和0.477。同时,理论仿真表明,在510 nm~590 nm和620 nm~700 nm范围内,该透镜具有连续宽带消色差超分辨聚焦能力。
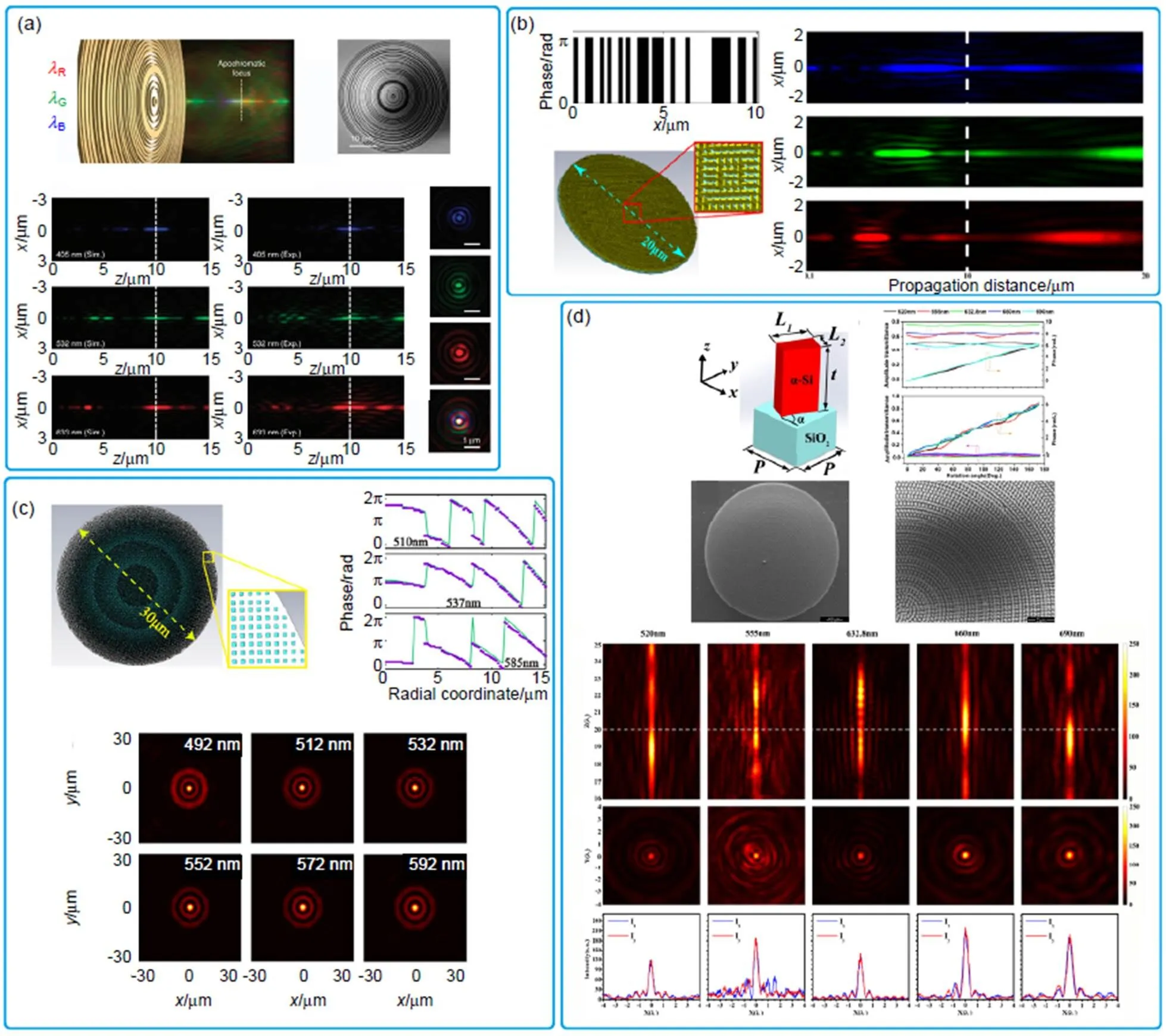
图3 多波长消色差超分辨超构透镜及聚焦实验、仿真结果。(a) 基于金属环带结构二值振幅调控的多波长消色差超分辨超构透镜及聚焦实验结果[42];(b) 基于多值相位调控的多波长消色差超分辨超构透镜及聚焦理论仿真结果[44];(c) 基于连续相位调控和色散调控多波长消色差超分辨超构透镜及聚焦仿真结果[45];(d) 基于全息方法的多波长消色差超分辨超构透镜及聚焦实验结果[47]
3.1.2 宽带消色差超分辨平面超构透镜
近年来,色散型超构表面[48]的出现,为平面超构透镜消色差提供了新的途径。利用超构表面色散工程,可以实现宽带连续消色差超构透镜。然而,受限于衍射效应,这些宽带连续消色差超构透镜无法突破衍射极限实现超分辨聚焦。针对上述问题,2019年,重庆大学提出了一种基于振幅调控和色散调控的宽带消色差超分辨平面超构透镜设计方法[49]。通过仿真发现,基于双曲面相位分布的传统超构透镜,当中心位置挡光时,其聚焦光场的横向偏振分量的横向尺寸会随挡光圆盘半径增加而减小。当数值孔径为0.95时,其极限横向尺寸可以达到0.38。基于这一特性,结合色散调控,利用色散型双条形结构,通过无需优化的消色差平面超构透镜设计方法[50],根据其群延迟大小,将具有不同群延迟的几何相位超表原子,从透镜中心向外排布。在中心位置采用透射率较低的超原子以实现振幅调控,进而实现整个器件宽带消色差超分辨聚焦功能。所报道的器件直径为10.22 mm,焦距为40.39 mm,其对应的数值孔径和衍射极限分别为=0.126和FWHMDL=3.983。在太赫兹波段111 µm~131 µm实现了连续宽带消色差超分辨聚焦,其焦斑尺寸3.617~3.764,小于相应的衍射极限。同样地,由于受限于色散型超原子集有限的群延迟范围,其难以实现大数值孔径或大口径的宽带连续消色差超分辨平面超构透镜。2021年,中国科学院光电技术研究所提出了一种宽带消色差超分辨超构透镜[51],其相位包括三个部分:针对中心波长传统聚焦透镜相位分布、二值相位滤波器和与色散有关的相位项。其中第一个相位分布用于实现光场聚焦、第二个相位用于实现超分辨,而色散项关系到透镜的色差消除。前两项通过几何相位实现,而色散项通过采用具有不同尺寸的几何相位超构表面单元,利用其传播相位,针对给定的多个波长,通过优化设计实现色差的消除。针对可见光范围内424.52 nm、444.66 nm、466.80 nm、491.26 nm、518.42 nm、548.77nm、582.89 nm、621.53 nm 和665.66 nm等9个波长进行消色差超分辨聚焦器件优化设计,透镜的数值孔径为0.16,理论仿真表明该透镜在400 nm~700 nm波长范围内,其焦斑半高全宽约为衍射极限0.66倍。

图4 基于振幅调控和色散调控的连续宽带消色差超分辨平面超构透镜[49]。(a) 实现相位调控和色散调控的双条形Si超表面结构;(b) 通过降低双曲面相位分布透镜中心区域的振幅透射率实现超分辨聚焦;(c) 消色差超分辨聚焦理论仿真结果;(d) 透镜的光学照片;(e) 透镜的消色差超分辨聚焦实验结果
目前,无论是超分辨平面超构透镜还是传统的消色差平面超构透镜,主要还是针对焦点处的色差矫正,并未考虑轴外色差和几何相差的矫正。在未考虑结构色散的消色差超分辨平面透镜设计中,往往是通过牺牲聚焦效率和轴向分辨率,来实现不同波长在设定焦平面上的超分辨聚焦;基于色散工程的宽带连续消色差超分辨平面透镜,由于受加工深宽比限制,其色散型超原子集有限的群延迟范围难以实现大数值孔径或大口径器件。实现宽带连续消色差的一种可行途径,就是结合传统折射型透镜和平面超构透镜,利用传统透镜的介质色散和平面超构透镜结构色散异号的特性,实现色差的矫正;同时,利用平面超构透镜波前调控功能,实现整个透镜的超分辨功能。
3.2 平场超分辨平面超构透镜
目前报道的大多数光学超分辨超构透镜在设计中,通常仅考虑了在正入射条件下焦点处的焦斑横向尺寸,往往忽略了轴外像差的矫正。因此,当入射角度发生较小(0.1°左右)的偏离时,其轴外聚焦光斑呈现迅速的恶化,导致透镜无法实现超分辨聚焦。然而,轴外像差的矫正,直接影响到平面超构透镜成像、光学扫描等,对于超分辨平面超构透镜的实际应用至关重要。通过对平面超构透镜的相位分布进行设计,可以实现宽角的一维傅里叶变换透镜,其角度范围可达到±60°[52];通过优化孔径光阑,可以使平面超构透镜实现宽角的一维平场聚焦,其角度范围为±40°[53];对双面超构透镜的入射透镜和聚焦透镜的相位分布进行优化[54-55],在数值孔径分别为0.44和0.45的条件下,可以分别实现±25°和±60°(0.45)的宽角平场聚焦平面超构透镜。2017年,中国科学院光电技术研究所提出了一种基于对称变换的宽角平面透镜[56],在数值孔径为0.89的情况下,其入射角可以高达80°。2021年,该研究所提出了一种高效率的流线型超构表面,在大角度下仍然具有极高的效率,并基于这种流线型超构表面,研制出了一种视场角高达178°的红外超构单透镜[57]。然而,这些传统平面超构透镜的聚焦光斑尺寸均无法突破光学衍射极限。由于超分辨平面超构透镜的设计无法采用现有的光学商业软件,因此对于平场超分辨平面超构透镜的设计很难直接使用常规设计手段,这极大地增加了平场超分辨平面超构透镜的设计难度。
2020年,重庆大学报道了一种高数值孔径平场超分辨平面超构透镜[58],其工作波长为=632.8 nm,采用基于准连续相位调控的单透镜结构,32个相位在0~2π范围内等间隔取值,相位调控通过-Si几何相位超构表面实现。该透镜半径为240,焦距为=60,数值孔径高达0.97,对应的衍射极限为FWHMDL=0.515。通过优化透镜相位分布,在入射角为±2°范围内,均可以在焦平面上实现超分辨聚焦,焦斑尺寸保持在0.45以下,且随着角度变化波动较小。焦斑在焦平面上偏移量与入射角度呈较好的线性关系,最大偏移量达到4。相较于具有相同参数的正入射超分辨聚焦平面超构透镜(超分辨聚焦工作角度范围仅为±0.3°),所报道的高数值孔径平场超分辨平面超构透镜,在±2°范围内,强度变化较小,旁瓣无明显增加。在实验上获得的焦斑横向尺寸在0.42~0.467范围内。同时,理论和实验研究发现,这种透镜其聚焦光场焦深较大,沿传播方向呈现光针形状,并且在焦深范围内(2~10)其横向尺寸大都小于衍射极限。进一步的研究表明,如果采用带孔径光阑的超分辨平面超构透镜,通过同时优化孔径光阑大小和透镜相位分布,可将超分辨聚焦工作角度范围进一步增加到±4.5°,同时进一步压缩焦斑横向尺寸至0.42以下。
2021年,中国科学院光电技术研究所提出了一种宽角平场超分辨平面超构透镜[59],其设计是基于传统衍射受限的超构表面双透镜[55-56]。首先通过优化前透镜(轴外相差矫正透镜)与后透镜(聚焦透镜)的相位分布,实现衍射受限的宽角聚焦功能;然后,在前透镜相位基础上叠加一个附加二值相位(0或π)滤波器相位模板,通过对模板相位分布进行优化,实现宽角超分辨聚焦。按入射孔径和后焦距计算,该透镜数值孔径约为0.447,对应的衍射极限为FWHMDL=1.136(0.719 µm)。其相位调控通过TiO2几何相位超构表面实现,通过CST仿真表明该透镜在入射角为±25°范围内,均能够实现超分辨聚焦。其焦斑横向尺寸在方向在0.750.78范围内变化,而在方向(偏转方向)其焦斑尺寸在0.7720.931内变化,且方向的焦斑尺寸随着角度增大而增大,直至超过衍射极限。
如何在压缩点扩散函数的前提下,大幅提升视场角,特别是实现大数值孔径宽角平场超分辨平面透镜,在成像和显微等应用方向具有重要的意义。这也对超构表面的角度不敏感性提出了很高的要求。通常随着入射角度的增大,超构表面的振幅、相位调控功能都会偏离正入射情形,这也为宽角超分辨平面超构透镜的设计提出了挑战。而由于超分辨衍射器件设计的特殊性,其通常需要大量耗时的衍射计算,计算量随着透镜尺寸的增加呈平方量级增加。随着焦斑尺寸的深度压缩,超构表面单元出射光场的准确分布以及超构表面单元之间的耦合无法忽略,这无疑将进一步增大平场超分辨平面超构透镜的设计难度。

图5 平场超分辨平面超构透镜及聚焦实验、仿真结果:(a) 基于连续相位调控的高数值孔径单透镜及 实验与理论仿真结果对比[58];(b) 基于二值相位超分辨模板的双透镜及仿真结果[59]
4 矢量超分辨平面超构透镜
矢量光场是指同一时刻在同一波阵面上不同位置的偏振态分布各不相同的光场,偏振态方向随着空间位置而变化。常见的矢量光场有径向偏振光场和角向偏振光场,其偏振方向分别是由光束中心指向径向方向和沿圆周方向。由于矢量光场独有的聚焦特性,其可以用于产生多种特殊光场分布,如纵向偏振聚焦光场、二维空心聚焦光场、三维空心聚焦光场等,这些光场在粒子操控[60-61]、粒子加速[62]、超分辨显微[63-64]、超高密度光数据存储[65]、超分辨光刻[66]等方向有着重要的应用前景。采用矢量超分辨平面超构透镜,容易实现复杂的超分辨光场。
4.1 基于振幅-相位调控的矢量超分辨平面超构透镜
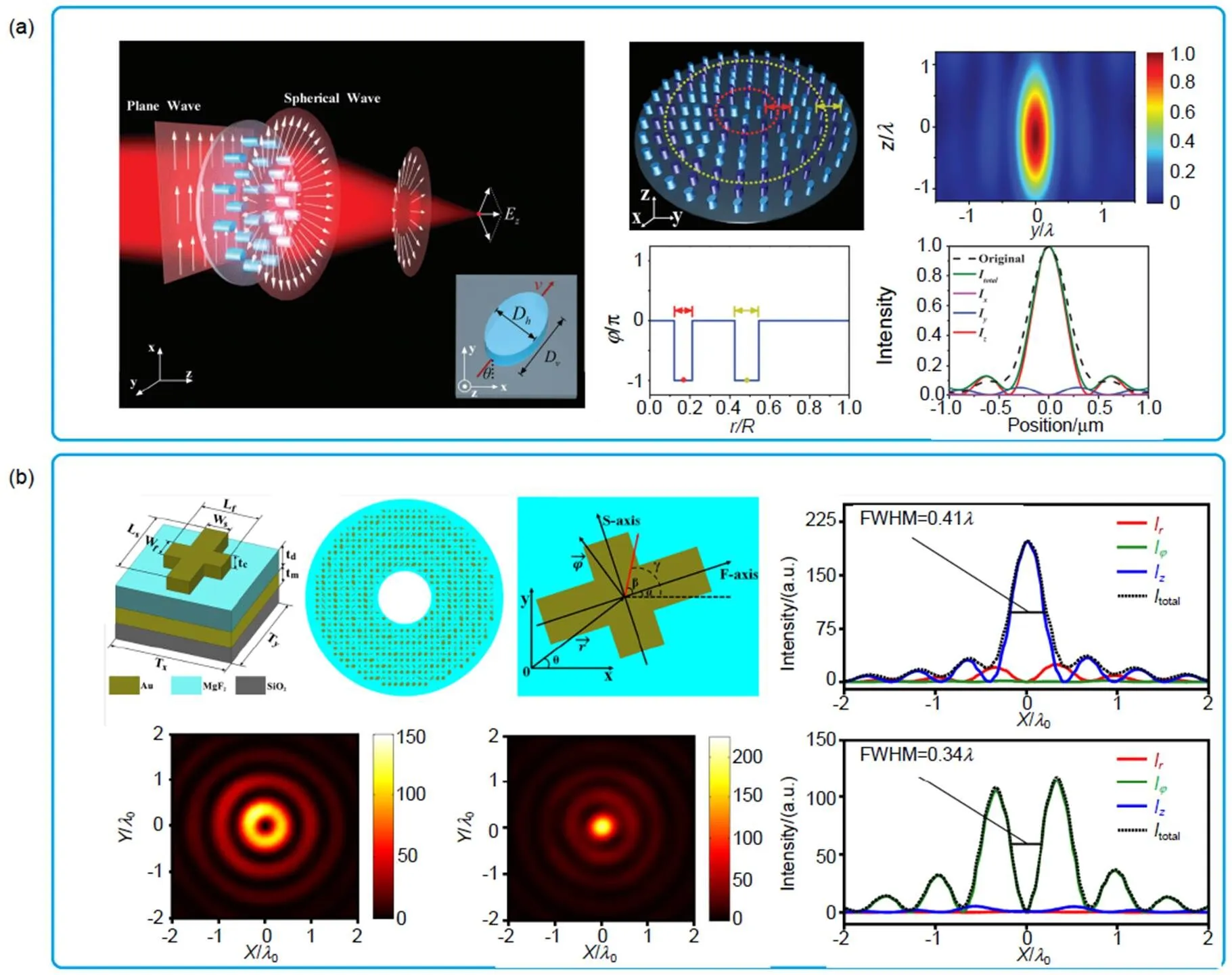
采用振幅相位调控是实现矢量超分辨平面超构透镜的最简单途径。在这种情况下,入射光束通常是由偏振转换片,将圆偏振光或是线偏振光,转化成为径向偏振光和角向偏振光;然后通过振幅-相位偏振调控,来实现对矢量光场超分辨聚焦。基于二值相位调控和二值振幅调控,重庆大学先后报道了径向偏振超分辨聚焦平面超构透镜[67]、角向偏振超分辨聚焦平面超构透镜[68-69]、角向偏振光针超分辨聚焦平场超构透镜[70]和三维空心光场超分辨聚焦平场超构透镜[71]。这种二值相位调控的矢量超分辨平面超构透镜结构简单易于加工,但在使用时需要将矢量光束中心与平面超构透镜中心同轴对准。而且简单的二值相位或二值振幅调控,极大地限制了器件对矢量光场调控的能力和器件的性能。

图6 三维空心光场矢量超分辨平面超构透镜及聚焦实验、仿真结果。(a) 基于二值相位调控的矢量超分辨平面超构透镜及其理论仿真和实验结果对比[71];(b) 基于角向偏振和径向偏振二值-相位独立调控的矢量超分辨平面超构透镜及其理论仿真结果[72]
采用超构表面,可以实现不同偏振态光场的独立调控,有利于提升矢量超分辨平场超构透镜的性能。2019年,重庆大学提出了一种能够实现径向偏振光和角向偏振光独立调控的三维空心球超分辨平面超构透镜[72]。采用4种超构表面单元结构,其快轴和慢轴的绝对相位差分别为(0,0)、(0,π)、(π,0)和(π,π),可对径向偏振和角向偏振态进行独立的二值相位调控,由此实现了径向偏振超构透镜与角向偏振超构透镜的空间重叠以及径向偏振聚焦功能和角向偏振聚焦功能的集成。通过独立设计径向偏振聚焦光场和角向偏振聚焦光场,使得三维空心聚焦光场的横向尺寸和轴向尺寸实现最优化。该透镜数值孔径为0.946,采用FDTD进行仿真发现,在设计波长=632.8 nm下,聚焦光场内径横向半高全宽为0.33、纵向半高全宽为1.33。相对于简单的二值调控方法[71],其横向半高全宽得到了极大地压缩。进一步的数值仿真研究发现,该器件在612.8 nm~652.8 nm范围内,均能产生三维空心超分辨聚焦光场,实现了宽带聚焦。
4.2 基于相位-偏振调控的矢量超分辨平面超构透镜
采用相位-偏振独立调控超构表面,可实现波前调控功能和偏振转换功能的集成,并实现矢量偏振光束与超构透镜的自对准,极大降低矢量超分辨平面超构透镜使用难度。
2018年,南开大学和山西大学共同提出了一种基于二分之一波片全介质超构表面的准连续相位调控矢量光场产生与波前调控平面超构透镜[73]。该透镜由30种具有不同尺寸和不同初始相位的二分之一波片全介质椭圆柱作为基本单元,其初始相位等间隔分布在0~2π之间。利用二分之一波片对线偏振入射光的偏振连续调控功能,通过旋转二分之一波片超构表面单元结构,实现出射偏振方向的连续调控;并利用30个不同初始相位的二分之一波片全介质椭圆柱,实现相位的准连续调控。进而在亚波长尺度下实现相位和偏振的独立调控。该透镜相位分布由两个相位分布相加构成,包括通常使用的双曲面透镜相位分布和二值相位模板(0和π)相位分布。通过优化二值相位模板的相位分布,实现超分辨聚焦。该透镜数值孔径约为=0.96,理论仿真表明在870 nm~1130 nm波长范围内均能实现超分辨聚焦,而聚焦光斑强度随着波长的改变,有明显的变化。
2019年,重庆大学提出了一种基于四分之一波片超构表面的准连续相位调控矢量光场产生与波前调控平面超构透镜[74]。该透镜由32个“十”字形超构表面单元结构所构成,每个结构单元具有不同的初始相位,等间隔分布在0~2π之间。利用四分之一波片对圆偏振光的偏振转换功能,这些四分之一波片超构表面单元结构可以将入射圆偏振光转化成为线偏振光,并可以通过旋转四分之一波片实现出射线偏振光方向的偏转;同时,可以利用32个四分之一波片的初始相位,实现对光场的相位调控;进而在亚波长尺度下实现相位和偏振的独立调控。直接采用常用的双曲面相位分布形式,分别设计了两个数值孔径为0.96的径向偏振聚焦超构透镜和角向偏振聚焦超构透镜。通过FDTD仿真发现,两个透镜在1490 nm~1700 nm波长范围内均能实现超分辨聚焦,而且均表现出消色差能力。特别是角向偏振聚焦超构透镜,在上述整个波长范围内均实现了消色差超分辨聚焦,形成的角向偏振空心焦斑内径半高全宽均小于0.34。而径向偏振聚焦超构透镜在1490 nm~1590 nm和1590 nm~1700 nm两个波长范围分别具有宽带消色差超分辨聚焦性能,其聚焦光斑尺寸在0.38~0.45范围内变化。
尽管上述两类超构透镜可以实现独立的连续偏振调控和准连续的相位调控,然而由于涉及的超构表面尺寸变化较大,存在一定的加工难度。为了解决这一问题,2020年,重庆大学提出了一种基于单个二分之一波片超构表面的矢量超分辨平面超构透镜[75]。该透镜充分利用了二分之一波片的连续偏振调控和二值相位调控特性。在线偏振光入射情况下,旋转二分之一波片,则出射光为线偏振光,而且其线偏振方向随着波片旋转而发生偏转,偏振方向偏转角为波片旋转角的两倍;当旋转角度大于180°时,可以看作是出射线偏振方向旋转了2×(-180°),而相位改变为π。由此,可以采用单个二分之一波片超构表面单元结构,实现独立的连续偏振调控和二值相位调控,这极大地降低了器件的加工难度。该透镜半径为158 µm,焦距为63.3 µm(@632.8 nm),对应的数值孔径和衍射极限分别为=0.93和FWHMDL=0.538,其能将入射线偏振光转化成为角向偏振光并聚焦成为角向偏振的超分辨空心焦斑。实验表明,该器件在518 nm~683.5 nm波长范围内均能实现超分辨聚焦,其对应的空心焦斑内径半高全宽在0.355~0.49范围内变化。
4.3 其他超分辨透镜
目前大多数报道的超分辨透镜都是工作在空气环境下,为了进一步提高超分辨透镜的绝对分辨率,通常可以采用类似的传统透镜方法,即采用水或者油等作为工作介质,以进一步对焦斑的绝对尺寸进行压缩。2021年,太原理工大学和暨南大学提出了一种具有环境鲁棒性的液侵超临界透镜[76],该透镜设计在折射率分别为1.0、1.33和1.51的空气、水和油环境,透镜采用二值振幅设计,数值孔径为0.83,在入射波长为632.8 nm条件下,其聚焦光斑尺寸在三种介质中均能保持317±7 nm,约为衍射极限的0.69倍。通常超分辨透镜,都可以工作在不同的工作介质之中,当最小特征尺寸大于一个波长的时候,通常改变传播介质不会对传播光束的角谱有太大改变,即光场的空间频谱不会有太大改变,因此表现出焦斑尺寸对工作介质环境的鲁棒性;而工作折射率的改变,仅仅是改变焦点位置,通常随着介质折射率的增大,焦距增大。实际上,可以专门针对水环境和油环境对超分辨透镜进行优化设计,以极大提升超分辨透镜的绝对分辨率。2020年,暨南大学针对超分辨透镜聚焦旁瓣较大的问题,提出了一种两个对称的月牙形金属孔透镜[77],通过优化其几何尺寸和间隔,产生超分辨聚焦光场,理论仿真表明,在沿镜像对称轴方向无大的旁瓣。实验上,当焦斑尺寸为0.36时,沿该方向旁瓣与主瓣强度比约在10%以内。然而在其他方向,巨大的旁瓣依然无法消除。同时由于采用两个小孔实现聚焦,不利于超分辨透镜聚焦效率的进一步提高。
5 超分辨聚焦光场表征技术
5.1 数字相机接触式探测
聚焦光场测量最简单的方法,就是直接采用探测器阵列。特别是当相机光敏感元尺寸远小于波长的情况下,可以直接采用相机获取超分辨聚焦光场的空间强度分布。文献[78]报道了采用太赫兹微测辐射热测定焦平面阵列,测量由全介质超构透镜产生太赫兹亚波长紧聚焦光斑。超构透镜的数值孔径为0.95,聚焦光场的波长为118.8 µm,其焦斑尺寸在和两个正交方向分别为0.45和0.61,方向的焦斑尺寸小于衍射极限,而方向的焦斑尺寸大于衍射极限,其原因是由于入射光的偏振方向为方向,紧聚焦形成的纵向偏振聚焦光场导致焦斑方向变大。实验中所采用的焦平面阵列单元尺寸为17 µm×17 µm,仅为波长的0.143倍,完全可以满足对应波长下的超分辨光场的直接测量。其最大优点是测试速度快,但无法区分测量光场三个正交偏振分量,而且其是一种接触式测量方法。
5.2 刀口光场扫描及重建
刀口法是采用边缘平整的刀口,并结合光电探测器,对光场的强度分布进行逐点扫描,最后利用相应的重构算法对被测量的光场强度进行重建[79]。该方法是一种接触式测量方法,一方面刀口本身会对光场产生衍射作用,同时探测器也是与被检测光场直接接触。因此,为了减小刀口本身对光的衍射效应的影响,通常需要将刀口本身做薄,并且需要尽可能减小刀口边沿的粗糙度。将刀口直接制作在探测表面,可以降低由于刀口衍射带来的误差[80-81]。光场强度重构,通常采用Radon逆变换[82]来实现。由于是一种接触式测量,刀口的厚度和粗糙度引起的边缘散射以及空间扫描分辨率等对光场强度重建结果影响较大,特别是在超分辨光场测量当中,通常其测量结果有着明显的变形。由于采用逐点扫描方式,也极大地制约了其光场表征速度。同时,其只能对光场的总强度进行表征,不能区分各偏振分量的强度分布。
5.3 纳米探针光场扫描
纳米光纤探针通常用于近场光场分布的测量[5],可以将近场光转变成为可以传播的光,进而将光场能量耦合入探针,并通过光纤导入探测器进行测量。对于传播场的测量,仍然可以采用这种方式。然而,这种探针通常具有较强的偏振选择性[34, 83],仅能对与探针端面平行的电场分量进行耦合,但无法区分该面内偏振的具体方向。其空间分辨率主要取决于探针的孔径,分辨率可以高达30 nm[84]。由于其是一种接触式测量,而探针所采集信号微弱,并且具有很强的偏振选择性,因此很容易导致所测量光场结果与实际光场分布的偏离。同时由于其属于逐点扫描探测,因此测量速度慢,容易受到外界震动干扰。
5.4 基于偏振转换的共聚焦光场扫描
聚焦光场中的纵向偏振分量测量一直是聚焦光场的测试难点,特别是如何实现一种非接触式光场测量方法尤其重要。2013年法国贝桑松大学提出了一种基于偏振转换和空间模式滤波的共聚焦纵向偏振光场强度分布测量方法[85]。其测试系统是在一个共聚焦显微构架上,采用小数值孔径(=0.1)物镜替代显微筒镜,并在两个物镜之间加入偏振转换片(径向偏振-线偏振)和线偏振片。将第一个物镜(=0.8)准直后的光束进行偏振转换和选择,即将准直光束中的径向偏振分量转化成为线偏振分量,并通过线偏振片控制出射光束的偏振成分(仅让原入射光中的径向偏振分量通过)。在第二个物镜(=0.1)的焦平面上形成特定的横向模式。最后利用单模光纤的横向模式滤波功能,仅让原入射光中的径向偏振分量进入光纤,并通过光电探测器测量其强度。通过移动被检测光场,进行逐点扫描,就可以对第一个物镜焦平面上光场的纵向偏振分量分布进行绘制。类似地利用该系统,还可以对光场中的纵向偏振磁矢量进行测量。该方法的最大优点是实现了纵向偏振分量的非接触测量。然而,由于需要逐点扫描,其测量速度极慢,难以应用于实时的光场测量。
5.5 基于光学显微的聚焦光场直接成像
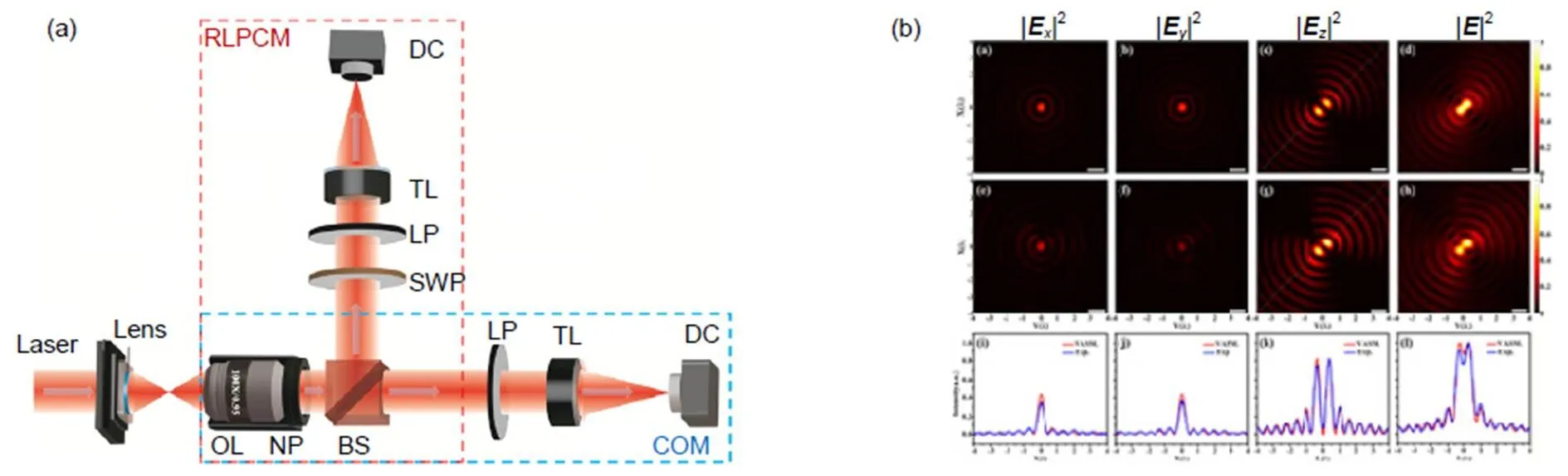
通常认为由传播波形成的超分辨聚焦光场,可以采用传统光学显微系统进行表征。该方法最大的优点是非接触式测量,不会对被检测光场产生影响。同时,借助于数字相机,可以实现对超分辨聚焦光场的快速测量。在可见光波段,由于相机像素尺寸远远大于光波长,为了准确地反映超分辨光场分布,必须采用大数值孔径、高放大倍率显微系统。然而,高放大倍率带来的偏振滤波效应,使得聚焦光场中的纵向偏振分量无法通过传统显微系统成像[34, 86]。因此,传统显微系统光学系统,通常应用于聚焦光场中的横向偏振分量强度空间分布的测量。尽管其已经成功地应用于各种横向偏振超分辨光场的测量,然而其合理性并未有严格的理论证明。2021年,重庆大学提出了一种传统光学显微系统光场测量模型[87],基于矢量角谱衍射方法[5],证明了在无限远光学显微系统筒镜后焦平面获得光场强度分布,与其物镜前焦平面上的聚焦光场横向偏振光强度分布具有相同形式,仅仅是简单的横向放大,其放大倍数即为显微系统的放大倍数。在此基础上,针对聚焦光场中的纵向偏振强度分布测量,进一步提出了一种基于偏振转换光学显微的聚焦光场纵向偏振分量强度分布直接显微成像理论模型和实现方法[87]。该方法是在传统的大数值孔径、高放大倍率的无限远光学显微系统的物镜和筒镜之间,沿光路传播方向以此放入偏振转换片和线偏振片,其中偏振转换片将经过物镜准直后的光场中的径向偏振分量转化为线偏振分量,而后续的线偏振片仅允许由径向偏振光转化成的线偏振光通过筒镜。通过理论证明,此时在筒镜后焦平面获得光场强度分布,与其物镜前焦平面上的聚焦光场纵向偏振光强度分布具有相同形式,仅仅是简单的横向放大,其放大倍数即为显微系统的放大倍数。

图8 基于光学显微的聚焦光场直接成像[87]。(a) 系统结构原理图;(b) 线偏振(45°)聚焦光场聚焦光场各分量和总光场强度的理论(第一行)与实验(第二行)结果对比
基于上述理论,采用两套相同的高数值孔径、高放大倍率无限远光学显微系统(共用一个显微物镜),分别构成横向偏振分量强度分布表征模块和纵向偏振分量强度分布表征模块。该系统已经成功地应用于标量光场聚焦光斑和矢量偏振聚焦光斑测试[87],其测试结果与理论仿真结果高度吻合。通过在物镜上加装单轴纳米位移定位系统,可以实现对聚焦光场中三个偏振分量空间三维分布的快速测量。在横向偏振分量强度测量中,还可以增加四分之一波片,通过测量斯托克斯参数,进而实现三维矢量光场的全偏振参数测量。
这些表征技术各有自身的优缺点。基于显微系统表征方法,受显微系统数值孔径的限制,难以实现对数值孔径大于显微系统数值孔径的超分辨透镜聚焦光场进行准确的测量,通常这可能会导致焦斑测量尺寸的扩大或无法观测。此时,可以采用纳米探针光场扫描方式进行光场表征。当聚焦光斑尺寸远大于数字相机像元尺寸时,如果不考虑偏振测量问题(特别是纵向偏振),可以直接采用数字相机对光场进行直接表征。同时,目前的光场测量中主要是针对电场分量,而较少考虑磁场分量,相关技术也亟待进一步开展研究。
6 超分辨透镜应用
超分辨光学器件已经成功地应用于超分辨光学显微[88‒90]和超分辨望远[91]等,下面我们将对超分辨透镜应用的最新进展进行总结。
6.1 超分辨透镜直接成像
针对超分辨光学成像,2018年开放大学、南安普顿大学和南洋理工大学等共同提出了一种超分辨成像透镜的设计方法[92]。该方法利用圆长椭球函数[93]作为基函数,利用其带宽有限特性等,对超分辨透镜的视场范围和点扩散函数尺寸进行独立设计。并通过数值仿真验证了所设计透镜的超分辨成像性能,通过优化视场和点扩散函数尺寸,成像分辨率达到了0.4。
6.2 超分辨光学共聚焦显微
提高相位调控的空间分辨率和相位调控自由度,有利于实现超分辨器件焦斑的深度压缩。2019年,南洋理工大学和南安普顿大学共同提出了一种超高有效数值孔径的超分辨聚焦超构透镜[94]。针对近红外波长=800 nm,采用8种“V”形纳米孔结构,实现[0,π)之间的8个等间隔相位调控,其单元尺寸仅为0.375。该透镜实现了半高全宽为0.33的超分辨聚焦光斑,有效数值孔径达到1.52。利用该透镜作为共聚焦显微系统的照明透镜,通过移动样品实现了超分辨共聚焦扫描成像,可以清晰分辨直径为160 nm、间隔280 nm双孔结构。2020年,南安普顿大学和南洋理工大学共同报道了一种基于超分辨透镜的共聚焦显微非标记生物成像[95-96],该系统采用了两个空间光调制器,在波长=488 nm实现了直径为0.4的超分辨照明焦斑,采用扫描镜实现了30帧/秒的成像速度,每帧像素为512×512,相对于传统的明场显微成像分辨率提高了1.5倍,而照明光强相对于传统荧光显微降低了1~2个数量级。该系统进一步采用了偏振增强技术[97-98],实现透明生物样品的超分辨显微成像。2020年,西北工业大学采用一种台阶式多值相位调控方式,实现了尺寸为毫米级的超分辨透镜[99]。采用该透镜聚焦光斑作为荧光显微的照明光斑,提高了传统荧光光学显微的分辨率。但由于所采用工艺限制,其台阶环带宽度为5 µm,远大于工作波长,导致其难以实现亚波长量级的超分辨聚焦,其焦斑理论尺寸为1.12(小于对应的瑞利衍射极限0.61/=1.36,但略大于阿贝衍射极限0.5/=1.118)。

图9 超分辨透镜应用。(a) 超分辨透镜直接成像理论仿真[92];(b), (c) 超分辨透镜应用于非标记超分辨光学显微[94-96];(d) 基于超振荡干涉仪的超精密位移测量[100]
6.3 超分辨光尺
超分辨光场的形成,通常伴随着局部π相位跳变,这种局部相位跳变导致了巨大的局域波矢,同时这种局部跳变也将这种巨大的局域波矢限制在极小的空间区域。在近红外波段和可见光,这一区域仅在几个纳米左右。而其局域波矢空间分布的自相关函数在很小的距离范围内以指数衰减,理论上可以达到0.19 nm的空间分辨率。可以利用这一极小的区域作为光尺的“刻度”,实现高精密的位移测量。基于这一原理,南洋理工大学和南安普顿大学共同提出了一种纳米级光尺测量方法[100]。该测量技术采用了一种基于几何相位超构表面的集成化微型干涉板[101],集成了一个超振荡透镜和一个参考光束产生器。由超振荡透镜产生的超振荡光场与参考光形成的干涉条纹可以通过一个显微系统获取。根据干涉条纹,通过计算得到超振荡透镜所产生超振荡光场的空间相位分布(其中包括了相位跳变的超振荡区域),进而可以得到空间局部波矢的空间分布,即超分辨光尺的“刻度”。通过观察“刻度”移动,便可以得到相应的位移量。理论上该技术位移分辨力可以达到/4000,但由于纳米机械运动、像元尺寸等因素影响,实验上仅实现1.5 nm的分辨力。同时该研究还展示了二维位移测量,其位移分辨率达到了2.2 nm。
7 总结与展望
光学超分辨超构透镜为从器件层面突破衍射极限瓶颈、研制新型的远场超分辨成像系统提供了一种崭新的途径,相关理论和技术已经在超分辨成像和超分辨显微中得到了应用。特别是近年来,随着光学超构表面的发展,极大地推动了光学超分辨超构透镜相关研究。然而,光学超分辨超构透镜的发展还存在诸多问题有待进一步深入研究。尽管在理论上可以实现任意小的焦斑,然而目前实验报道的焦斑尺寸仅仅在0.3这一水平。这一方面受限于目前的设计手段,特别是衍射计算的准确性;另一方面在设计中目前还无法准确获取器件表面实际光场分布,特别是超构表面单元结构之间的耦合。这导致了理论设计和实际情况之间的差异,特别是当焦斑尺寸小于0.3时,这些因素的影响将无法忽略。同时,随着焦斑尺寸减小,通常对波前调控的空间分辨率就越高,这对于单元尺寸有限的超构表面超分辨透镜无疑将是一种挑战。一种可能的解决途径是采用连续面形变化介质曲面,然而,这将极大地增加依赖于衍射计算的超分辨透镜设计难度。如何快速、准确地实现衍射计算(特别是曲面衍射),也是超分辨超构透镜面临的难题,特别是对于非圆对称的目标光场,大尺寸透镜、平场透镜等设计难度极大。对于消色差超分辨超构透镜,目前最大的难点就是如何在实现宽带超分辨消色差的同时,有效地提高透镜的数值孔径和口径,单纯采用色散型超构表面难以满足大数值孔径和大口径超分辨超构透镜消色差对群延迟范围的要求。一种可能的途径,就是结合传统介质透镜和超构表面,利用材料色散补偿结构色散,结合超分辨透镜设计,实现大数值孔径、大口径宽带消色差超分辨超构透镜。目前的超分辨平场超构透镜,还未能有效地解决焦斑尺寸和视场角之间的矛盾,即便在较小的视场角下,也未能实现超振荡聚焦。特别是对于单透镜而言,由于设计自由度小,难以实现超分辨轴外相差的消除,其一种可能的途径是采用超构透镜组。在超分辨光场测试方面,如何实现超大数值孔径(数值孔径接近于1,但有效孔径远超1)超分辨透镜聚焦光场的快速测试,仍然具有挑战,尽管光学显微方法可以实现快速的超分辨光场测试,然而当超分辨透镜的数值孔径大于光学显微物镜数值孔径的时候,将导致超分辨光场细节的消失。可能的解决途径是采用超构透镜实现数值孔径为1的物镜(空气中)来取代传统物镜,使显微系统能够接收来自大数值孔径超分辨超构透镜的所有出射光场。尽管面临诸多挑战,超振荡光学器件在远场超分辨显微、成像和超高密度数据存储等方面,已初步显示出良好的应用前景。随着光学超振荡、超振荡光学器件及系统相关理论和技术研究的不断深入,有望在光学器件层面突破衍射极限制约,推动超分辨显微、超分辨成像、光学纳米操控、纳米光学加工、超高密度数据存储、激光聚焦等技术进一步发展。
[1] Lipson S G, Lipson H, Tannhauser D S.[M]. New York: Cambridge University Press, 1995.
[2] Gan F X, Wang Y. Breaking through the optical diffraction limits, developing the nano-optics and photonics[J]., 2011, 31(9): 0900104.
干福熹, 王阳. 突破光学衍射极限, 发展纳米光学和光子学[J]. 光学学报, 2011, 31(9): 0900104.
[3] Li S, Kuang C F, Ding Z H,A review on concept and development of stimulated emission depletion microscopy (STED)[J]., 2013, 22(2): 103–113.
李帅, 匡翠方, 丁志华, 等. 受激发射损耗显微术(STED)的机理及进展研究[J]. 激光生物学报, 2013, 22(2): 103–113.
[4] Dan D, Lei M, Yao B L,. DMD-based LED-illumination Super-resolution and optical sectioning microscopy[J]., 2013, 3(1): 1116.
[5] Novotny L,Hecht B.[M]. 2nd ed. Cambridge: Cambridge University Press, 2012.
[6] Pan L, Park Y, Xiong Y,. Maskless plasmonic lithography at 22 nm resolution[J]., 2011, 1(1): 175.
[7] Zhang X, Liu Z W. Superlenses to overcome the diffraction limit[J]., 2008, 7(6): 435–441.
[8] Aieta F, Genevet P, Kats M A,. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces[J]., 2012, 12(9): 4932–4936.
[9] Ishii S, Shalaev V M, Kildishev A V. Holey-metal lenses: sieving single modes with proper phases[J]., 2013, 13(1): 159–163.
[10] Saxena S, Chaudhary R P, Singh A,. Plasmonic micro lens for extraordinary transmission of broadband light[J]., 2014, 4(1): 5586.
[11] Dong J J, Liu J, Hu B,. Subwavelength light focusing with a single slit lens based on the spatial multiplexing of chirped surface gratings[J]., 2014, 104(1): 011115.
[12] Huang F M, Chen Y F, de Abajo F J G,. Optical super-resolution through super-oscillations[J]., 2007, 9(9): S285–S288.
[13] Huang F M, Zheludev N I. Super-resolution without evanescent waves[J]., 2009, 9(3): 1249–1254.
[14] Wen Z Q, He Y H, Li Y Y,. Super-oscillation focusing lens based on continuous amplitude and binary phase modulation[J]., 2014, 22(18): 22163–22171.
[15] He Q, Sun S L, Xiao S Y,. High-efficiency metasurfaces: principles, realizations, and applications[J]., 2018, 6(19): 1800415.
[16] Chen S Q, Li Z, Zhang Y B,. Phase manipulation of electromagnetic waves with metasurfaces and its applications in nanophotonics[J]., 2018, 6(13): 1800104.
[17] Luo X G. Subwavelength optical engineering with metasurface waves[J]., 2018, 6(7): 1701201.
[18] Neshev D, Aharonovich I. Optical metasurfaces: new generation building blocks for multi-functional optics[J]., 2018, 7: 58.
[19] Su V C, Cheng H C, Sun G,. Advances in optical metasurfaces: fabrication and applications [Invited][J]., 2018, 26(10): 13148–13182.
[20] Pu M B, Guo Y H, Ma X L,. Methodologies for on-demand dispersion engineering of waves in metasurfaces[J]., 2019, 7(14): 1801376.
[21] Lin D M, Fan P Y, Hasman E,. Dielectric gradient metasurface optical elements[J]., 2014, 345(6194): 298–302.
[22] Jahani S, Jacob Z. All-dielectric metamaterials[J]., 2016, 11(1): 23–36.
[23] Khorasaninejad M, Chen W T, Devlin R C,. Metalenses at visible wavelengths: diffraction-limited focusing and subwavelength resolution imaging[J]., 2016, 352(6290): 1190–1194.
[24] Arbabi A, Horie Y, Bagheri M,. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission[J]., 2015, 10(11): 937–943.
[25] Arbabi E, Arbabi M, Kamali S M,. Multiwavelength polarization-insensitive lenses based on dielectric metasurfaces with meta-molecules[J]., 2016, 3(6): 628–633.
[26] Jia D L, Tian Y, Ma W,. Transmissive terahertz metalens with full phase control based on a dielectric metasurface[J]., 2017, 42(21): 4494–4497.
[27] Jiang X, Chen H, Li Z Y,. All-dielectric metalens for terahertz wave imaging[J]., 2018, 26(11): 14132–14142.
[28] Chen H, Wu Z X, Li Z Y,. Sub-wavelength tight-focusing of terahertz waves by polarization-independent high-numerical-aperture dielectric metalens[J]., 2018, 26(23): 29817–29825.
[29] Hu Y Q, Wang X D, Luo X H,. All-dielectric metasurfaces for polarization manipulation: principles and emerging applications[J]., 2020, 9(12): 3755–3780.
[30] Dong Y, Xu Z J, Li N X,. Si metasurface half-wave plates demonstrated on a 12-inch CMOS platform[J]., 2020, 9(1): 149–157.
[31] Kruk S, Hopkins B, Kravchenko I I,. Invited Article: broadband highly efficient dielectric metadevices for polarization control[J]., 2016, 1(3): 030801.
[32] Chen C, Gao S L, Xiao X J,. Highly efficient metasurface quarter-wave plate with wave front engineering[J]., 2021, 2(3): 2000154.
[33] Zhang Y B, Liu H, Cheng H,. Multidimensional manipulation of wave fields based on artificial microstructures[J].-, 2020, 3(11): 200002.
[34] Grosjean T, Courjon D. Polarization filtering induced by imaging systems: effect on image structure[J]., 2003, 67(4): 046611.
[35] Rogers E T F, Zheludev N I. Optical super-oscillations: sub-wavelength light focusing and super-resolution imaging[J]., 2013, 15(9): 094008.
[36] Chen G, Wen Z Q, Wu Z X. Optical super-oscillation and super-oscillatory optical devices[J]., 2017, 66(14): 144205.
陈刚, 温中泉, 武志翔. 光学超振荡与超振荡光学器件[J]. 物理学报, 2017, 66(14): 144205.
[37] Berry M, Zheludev N, Aharonov Y,. Roadmap on superoscillations[J]., 2019, 21(5): 053002.
[38] Chen G, Wen Z Q, Qiu C W. Superoscillation: from physics to optical applications[J]., 2019, 8: 56.
[39] Rogers K S, Rogers E T F. Realising superoscillations: a review of mathematical tools and their application[J]., 2020, 2(4): 042004.
[40] Zheludev N I, Yuan G H. Optical superoscillation technologies beyond the diffraction limit[J]., 2022, 4(1): 16–32.
[41] Wang H T, Hao C L, Lin H,. Generation of super-resolved optical needle and multifocal array using graphene oxide metalenses[J]., 2021, 4(2): 200031.
[42] Yuan G H, Rogers E T F, Zheludev N I. Achromatic super-oscillatory lenses with sub-wavelength focusing[J]., 2017, 6(9): e17036.
[43] Jin N B, Rahmat-Samii Y. Advances in particle swarm optimization for antenna designs: real-number, binary, single-objective and multiobjective implementations[J]., 2007, 55(3): 556–567.
[44] Tang D L, Chen L, Liu J J. Visible achromatic super-oscillatory metasurfaces for sub-diffraction focusing[J]., 2019, 27(9): 12308–12316.
[45] Chen L, Liu J, Zhang X H,. Achromatic super-oscillatory metasurface through optimized multiwavelength functions for sub-diffraction focusing[J]., 2020, 45(20): 5772–5775.
[46] Lu X J, Guo Y H, Pu M B,. Switchable polarization-multiplexed super-oscillatory metasurfaces for achromatic sub-diffraction focusing[J]., 2020, 28(26): 39024–39037.
[47] Dai X M, Dong F L, Zhang K,. Holographic super-resolution metalens for achromatic sub-wavelength focusing[J]., 2021, 8(8): 2294–2303.
[48] Chen W T, Zhu A Y, Sanjeev V,. A broadband achromatic metalens for focusing and imaging in the visible[J]., 2018, 13(3): 220–226.
[49] Zhao F, Li Z P, Dai X M,. Broadband achromatic sub-diffraction focusing by an amplitude-modulated terahertz metalens[J]., 2020, 8(21): 2000842.
[50] Zhao F, Jiang X, Li S,. Optimization-free approach for broadband achromatic metalens of high-numerical-aperture with high-index dielectric metasurface[J]., 2019, 52(50): 505110.
[51] Lu X J, Guo Y H, Pu M B,. Broadband achromatic metasurfaces for sub-diffraction focusing in the visible[J]., 2021, 29(4): 5947–5958.
[52] Liu W W, Li Z C, Cheng H,. Metasurface enabled wide-angle fourier lens[J]., 2018, 30(23): 1706368.
[53] Kalvach A, Szabó Z. Aberration-free flat lens design for a wide range of incident angles[J]., 2016, 33(2): A66–A71.
[54] Groever B, Chen W T, Capasso F. Meta-lens doublet in the visible region[J]., 2017, 17(8): 4902–4907.
[55] Arbabi A, Arbabi E, Kamali S M,. Miniature optical planar camera based on a wide-angle metasurface doublet corrected for monochromatic aberrations[J]., 2016, 7: 13682.
[56] Pu M B, Li X, Guo Y H,. Nanoapertures with ordered rotations: symmetry transformation and wide-angle flat lensing[J]., 2017, 25(25): 31471–31477.
[57] Zhang F, Pu M B, Li X,. Extreme-angle silicon infrared optics enabled by streamlined surfaces[J]., 2021, 33(11): 2008157.
[58] Zhang Q, Dong F L, Li H X,. High-numerical-aperture dielectric metalens for super-resolution focusing of oblique incident light[J]., 2020, 8(9): 1901885.
[59] Li Z, Wang C T, Wang Y Q,. Super-oscillatory metasurface doublet for sub-diffraction focusing with a large incident angle[J]., 2021, 29(7): 9991–9999.
[60] Zhan Q W. Trapping metallic Rayleigh particles with radial polarization[J]., 2004, 12(15): 3377–3382.
[61] Liu W, Dong D S, Yang H,. Robust and high-speed rotation control in optical tweezers by using polarization synthesis based on heterodyne interference[J]., 2020, 3(8): 200022.
[62] Gupta D N, Kant N, Kim D E,. Electron acceleration to GeV energy by a radially polarized laser[J]., 2007, 368(5): 402–407.
[63] Kozawa Y, Matsunaga D, Sato S. Superresolution imaging via superoscillation focusing of a radially polarized beam[J]., 2018, 5(2): 86–92.
[64] Yu W T, Ji Z H, Dong D S,. Super-resolution deep imaging with hollow Bessel beam STED microscopy[J]., 2016, 10(1): 147–152.
[65] Jiang Y S, Li X P, Gu M. Generation of sub-diffraction-limited pure longitudinal magnetization by the inverse Faraday effect by tightly focusing an azimuthally polarized vortex beam[J]., 2013, 38(16): 2957–2960.
[66] Gan Z S, Cao Y Y, Evans R A,. Three-dimensional deep sub-diffraction optical beam lithography with 9 nm feature size[J]., 2013, 4: 2061.
[67] Yu A P, Chen G, Zhang Z H,. Creation of sub-diffraction longitudinally polarized spot by focusing radially polarized light with binary phase lens[J]., 2016, 6: 38859.
[68] Chen G, Wu Z X, Yu A P,. Generation of a sub-diffraction hollow ring by shaping an azimuthally polarized wave[J]., 2016, 6: 37776.
[69] Wu Z X, Jin Q J, Zhang K,. Binary-amplitude modulation based super-oscillatory focusing planar lens for azimuthally polarized wave[J]., 2018, 45(4): 170660.
[70] Chen G, Wu Z X, Yu A P,. Planar binary-phase lens for super-oscillatory optical hollow needles[J]., 2017, 7(1): 4697.
[71] Wu Z X, Jin Q J, Zhang S,. Generating a three-dimensional hollow spot with sub-diffraction transverse size by a focused cylindrical vector wave[J]., 2018, 26(7): 7866–7875.
[72] Wu Z X, Zhang Q, Jiang X,. Broadband integrated metalens for creating super-oscillation 3D hollow spot by independent control of azimuthally and radially polarized waves[J]., 2019, 52(41): 415103.
[73] Zuo R Z, Liu W W, Cheng H,. Breaking the diffraction limit with radially polarized light based on dielectric metalenses[J]., 2018, 6(21): 1800795.
[74] Li Y Y, Cao L Y, Wen Z Q,. Broadband quarter-wave birefringent meta-mirrors for generating sub-diffraction vector fields[J]., 2019, 44(1): 110–113.
[75] Wu Z X, Dong F L, Zhang S,. Broadband dielectric metalens for polarization manipulating and superoscillation focusing of visible light[J]., 2020, 7(1): 180–189.
[76] Zhang Z X, Li Z Y, Lei J,. Environmentally robust immersion supercritical lens with an invariable sub-diffraction-limited focal spot[J]., 2021, 46(10): 2296–2299.
[77] Hu Y W, Wang S W, Jia J H,. Optical superoscillatory waves without side lobes along a symmetric cut[J]., 2021, 3(4): 045002.
[78] Chen H, Wu Z X, Li Z Y,. Sub-wavelength tight-focusing of terahertz waves by polarization-independent high-numerical-aperture dielectric metalens[J]., 2018, 26(23): 29817–29825.
[79] Dorn R, Quabis S, Leuchs G. Sharper focus for a radially polarized light beam[J]., 2003, 91(23): 233901.
[80] Kitamura K, Sakai K, Noda S. Finite-difference time-domain (FDTD) analysis on the interaction between a metal block and a radially polarized focused beam[J]., 2011, 19(15): 13750–13756.
[81] Yang L X, Xie X S, Wang S C,. Minimized spot of annular radially polarized focusing beam[J]., 2013, 38(8): 1331–1333.
[82] Born M, Wolf E.:,[M]. New York: Cambridge University Press, 1999.
[83] Novotny L, Hecht B.[M]. 2nd ed. Cambridge: Cambridge University Press, 2012.
[84] Baumgartl J, Kosmeier S, Mazilu M,. Far field subwavelength focusing using optical eigenmodes[J]., 2011, 98(18): 181109.
[85] Ecoffey C, Grosjean T. Far-field mapping of the longitudinal magneticand electric optical fields[J]., 2013, 38(23): 4974–4977.
[86] Liu T, Yang S M, Jiang Z D. Electromagnetic exploration of far-field super-focusing nanostructured metasurfaces[J]., 2016, 24(15): 16297–16308.
[87] Gao J, Yan S K, Zhou Y,. Polarization-conversion microscopy for imaging the vectorial polarization distribution in focused light[J]., 2021, 8(7): 984–994.
[88] Rogers E T F, Lindberg J, Roy T,. A super-oscillatory lens optical microscope for subwavelength imaging[J]., 2012, 11(5): 432–435.
[89] Qin F, Huang K, Wu J F,. A supercritical lens optical label-free microscopy: sub-diffraction resolution and ultra-long working distance[J]., 2016, 29(8): 1602721.
[90] Matsunaga D, Kozawa Y, Sato S. Super-oscillation by higher-order radially polarized Laguerre-Gaussian beams[C]//, 2016.
[91] Wang C T, Tang D L, Wang Y Q,. Super-resolution optical telescopes with local light diffraction shrinkage[J]., 2015, 5: 18485.
[92] Rogers K S, Bourdakos K N, Yuan G H,. Optimising superoscillatory spots for far-field super-resolution imaging[J]., 2018, 26(7): 8095–8112.
[93] Karoui A, Moumni T. Spectral analysis of the finite Hankel transform and circular prolate spheroidal wave functions[J]., 2009, 233(2): 315–333.
[94] Yuan G H, Rogers K S, Rogers E T F,. Far-field superoscillatory metamaterial superlens[J]., 2019, 11(6): 064016.
[95] Rogers E T F, Quraishe S, Chad J E,. New super-oscillatory technology for unlabelled super-resolution cellular imaging with polarisation contrast[J]., 2017, 112(3): 186A.
[96] Rogers E T F, Quraishe S, Rogers K S,. Far-field unlabeled super-resolution imaging with superoscillatory illumination[J]., 2020, 5(6): 066107.
[97] Le Gratiet A, Dubreuil M, Rivet S,. Scanning Mueller polarimetric microscopy[J]., 2016, 41(18): 4336–4339.
[98] Mehta S B, Shribak M, Oldenbourg R. Polarized light imaging of birefringence and diattenuation at high resolution and high sensitivity[J]., 2013, 15(9): 094007.
[99] Li W L, He P, Yuan W Z,. Efficiency-enhanced and sidelobe-suppressed super-oscillatory lenses for sub-diffraction-limit fluorescence imaging with ultralong working distance[J]., 2020, 12(13): 7063–7071.
[100] Yuan G H, Zheludev N I. Detecting nanometric displacements with optical ruler metrology[J]., 2019, 364(6442): 771–775.
[101] Yuan G H, Rogers E T F, Zheludev N I. “Plasmonics” in free space: observation of giant wavevectors, vortices, and energy backflow in superoscillatory optical fields[J]., 2019, 8: 2.
Recent research progress in optical super-resolution planar meta-lenses
Zhou Yi1,2*, Liang Gaofeng1,2, Wen Zhongquan1,2, Zhang Zhihai1,2, Shang Zhengguo1,2, Chen Gang1,2
1College of Optoelectronic Engineering, Chongqing University, Chongqing 400044, China;2Key Laboratory of Optoelectronic Technology and Systems Ministry of Education, Chongqing University, Chongqing 400044, China
(a) The direct imaging of focused optical field based on the optical microscope; (b) The diagram of the system layout
Overview:Due to the optical diffraction limitation, conventional optical systems can hardly achieve a resolution less than 0.5/, whereis the wavelength of the light source and NA presents the numerical aperture of the objective. Breaking through the theoretical resolution limit in the optical mechanism and realizing super-resolution optical point-spread-function is important in achieving super-resolution focusing and imaging, which have great potential applications in laser processing, super-resolution microscopy and telescope systems. Many ideas have been provided before to surpass the theoretical resolution limit, such as stimulated emission depletion (STED), single-molecule localization (SML), and structured illumination microscopy (SIM), but most of these will require labeling the samples and thus causes changes of the molecule behaviors. Negative-index super lens, which has been proposed to reconstruct and capture evanescent fields, has not yet been applied as a practical imaging technique because of substantial technological challenges. In recent years, with the development of optical metasurfaces, it is possible to achieve independent control of the amplitude, phase, and polarization of the optical field on the sub-wavelength scale, which in turn provides a more flexible means for the development of a new type of super-resolution planar super-lens. Optical super-oscillation, which has been exploited worldwide recently, is a phenomenon that a band-limited wave to oscillate locally much faster than the highest Fourier component of the signal. In principle, a super-oscillatory lens could produce a focus of any prescribed size, which can be potentially used in super-resolution microscopy, high-resolution laser manufacturing, and telescopes. This article reviews the recent research progress of super-resolution planar metalenses based on optical metasurfaces and related testing techniques. We introduce different methods to produce multiple-wavelength achromatic super-resolution metalenses and corresponding focusing results, as well as the continuous broadband achromatic super-resolution metalenses. Meanwhile, we explain the ways to design vectorial super-resolution meta-lenses, such as by phase and polarization manipulations and show the corresponding results. A new idea using an optical microscope to directly image the focused optical field is elaborated and compared with other existing methods. Finally, we present the typical applications of super-resolution metalenses in some areas such as confocal microscopy, micro/nano fabrication and nanometic displacement detection. The problems faced in this field and future research priorities and directions are also discussed in this review paper.
Zhou Y, Liang G F, Wen Z Q,Recent research progress in optical super-resolution planar meta-lenses[J]., 2021, 48(12): 210399; DOI:10.12086/oee.2021.210399
Recent research progress in optical super-resolution planar meta-lenses
Zhou Yi1,2*, Liang Gaofeng1,2, Wen Zhongquan1,2, Zhang Zhihai1,2,Shang Zhengguo1,2, Chen Gang1,2
1College of Optoelectronic Engineering, Chongqing University, Chongqing 400044, China;2Key Laboratory of Optoelectronic Technology and Systems Ministry of Education, Chongqing University, Chongqing 400044, China
Breaking through the theoretical resolution limit on the optical mechanism and realizing super-resolution optical point-spread-function is important in achieving super-resolution focusing and imaging, which have great potential applications in laser processing, super-resolution microscopy, and telescope systems. In recent years, with the development of optical metasurfaces, it is capable to achieve independent control of the amplitude, phase, and polarization of the optical fields on the sub-wavelength scale, which in turn provides a more flexible means for the development of a new type of super-resolution planar super-lens. This article reviews the recent research progress of super-resolution planar meta-lenses based on the optical metasurfaces and related testing techniques. It also discusses the problems faced in this field and future research priorities and directions.
optical super-resolution; super-oscillation; planar lens; metasurface
10.12086/oee.2021.210399
O436.3
A
National Natural Science Foundation of China (61927818, 61575031) and National Program on Key Basic Research Project (2013CBA01700)
* E-mail: yi_zhou@cqu.edu.cn
周毅,梁高峰,温中泉,等. 光学超分辨平面超构透镜研究进展[J]. 光电工程,2021,48(12): 210399
Zhou Y, Liang G F, Wen Z Q,Recent research progress in optical super-resolution planar meta-lenses[J]., 2021, 48(12): 210399
2021-11-18;
2021-12-09
国家自然科学基金资助项目(61927818,61575031);国家重点基础研究发展计划资助项目(2013CBA01700)
周毅(1991-),男,博士,主要从事超分辨光学显微成像技术和光学相干断层成像技术(OCT)的研究。E-mail:yi_zhou@cqu.edu.cn

