基于ARIMA-RNN组合模型的云服务器老化预测方法
孟海宁,童新宇,石月开,朱磊,冯锴,黑新宏
(1.西安理工大学计算机科学与工程学院,陕西 西安 710048;2.陕西省网络计算与安全技术重点实验室,陕西 西安 710048)
1 引言
软件老化是影响软件系统可靠性的潜在因素,当长期运行的软件系统存在软件老化现象时,系统将出现性能下降、异常和错误增加,甚至死机[1]。软件老化是由操作系统可分配资源匮乏、碎片化严重以及内部错误积累(如内存泄漏和未释放的文件资源)造成的,而这些错误在软件测试阶段难以检测和消除[2]。云计算系统的体系结构复杂,系统内计算资源的申请和释放较为频繁,且云系统长期运行为云用户提供服务,因此云系统更容易出现软件老化现象,影响系统可用性和可靠性。
为了避免软件老化,Huang 等[3]提出了软件再生。它是一种主动预防性的容错技术,通过重置软件系统内部状态,防止系统未来发生重大故障。该过程通过有计划地重启系统,清理系统运行环境,使系统恢复到初始健康状态。然而软件再生操作将带来额外的系统开销,因此需要选择最佳时机进行软件再生。
为了减少软件再生给系统带来的时间和资源消耗的成本,学者们对软件老化趋势进行预测,计算老化阈值,在系统重大故障发生之前对系统进行软件再生。其中,Okamura 等[4]构造了基于马尔可夫链的响应时间序列,评估分布式服务器系统的软件老化趋势。Matos 等[5]针对Eucalyptus 云系统老化现象,提出了基于多阈值的时间序列预测方法,该方法求解得到最优再生时机,可减少系统停机时间并提高系统可靠性。Islam 等[6]针对亚马逊EC2云系统,采用神经网络和线性回归的方法,预测系统资源使用情况,为资源配置策略提供参考依据。Langner 等[7]发现运行于同一个基于内核的虚拟机(KVM,kernel-based virtual machine)之上的3 个虚拟机(VM,virtula machine)的CPU 占用率逐步升高,物理内存和交换区使用量逐渐消耗,继而出现VM 上HTTP 请求响应缓慢,最终导致整个系统老化。Kousiouris 等[8]采用人工神经网络的方法,预测云系统中VM 的性能。郑鹏飞等[9]提出运用多元时间序列模型分析软件老化的方法。林已杰等[10]针对服务器软件老化现象,提出了一种基于BP 神经网络和马尔可夫模型结合的方法对服务器关键资源进行预测。
综上所述,大多数学者关注时间序列分析或智能算法来预测软件老化趋势。时间序列分析法采用自回归移动平均(ARMA,autoregressive moving average)、粒子滤波等模型进行趋势预测[11-13],模型简单,但所需数据量大且对于波动较大的数据预测精度较低。智能算法包括神经网络、支持向量机等[14-15],该类算法在预测时间序列数据时,预测精度不高且收敛较慢。因此,仅采用单一模型进行软件老化预测,很难获得比较精确的预测结果。
本文探究基于OpenStack[16-17]的云服务器系统的软件老化问题,为实现软件再生机制提供理论依据。本文将整合移动平均自回归(ARIMA,autoregressive integrated moving average)模型与循环神经网络(RNN,recurrent neural network)模型结合,得到ARIMA-RNN 组合模型,对云服务器系统老化趋势进行预测。该方法克服了ARIMA 模型对波动较大的数据预测精度较低的局限性,解决了RNN模型预测收敛速度慢的问题,最终实现对云服务器系统的老化预测。此外,本文设计了负载实验方案,模拟云服务器系统实际工作状况,选择云服务器的性能服务参数响应时间和系统参数CPU 使用率作为衡量系统老化的重要指标,验证软件老化现象的存在,并预测系统老化趋势。
2 ARIMA-RNN 组合模型预测方法
基于ARIMA-RNN 组合模型的云服务器老化预测方法的工作流程包括4 个基本步骤:数据预处理、ARIMA 模型构建及数据拟合、RNN 模型构建,以及ARIMA-RNN 组合模型构建及数据预测。
2.1 数据预处理
对云服务器进行老化预测前,需对数据进行归一化预处理。这是因为云服务器系统性能参数的时间序列数据分布不均匀且数据变化幅度(标准差)较大,数据中含有奇异样本数据,预测时会减慢网络的学习和收敛速度。因此本文采用归一化处理方法,将云服务器原始数据映射到[−1,1],使预测模型收敛速度快,映射转换过程如式(1)所示。

其中,xmax是数据的最大值,xmean是数据的平均值,X是原始时间序列数据,X˙是预处理后的时间序列数据。
2.2 ARIMA 模型构建及数据拟合
构建ARIMA 模型时,需确定ARIMA 模型中的参数p、d、q。首先,通过单位根检验方法,对序列数据进行平稳性检验,若序列数据为非平稳时间序列则需反复进行差分处理,直到差分后的时间序列平稳为止。然后,计算自相关和偏自相关函数,确定自回归项p和移动平均项q的取值范围。最后,采用赤池信息量准则(AIC,Akaike information criterion)对p和q的取值进行最佳估计,计算对应ARIMA 模型的AIC 值,从而得到最佳ARIMA 模型。其中AIC 值反映了数据的拟合效果,AIC 值越小,则数据拟合效果越好。采用ARIMA 模型的数据预测过程如图1 所示。
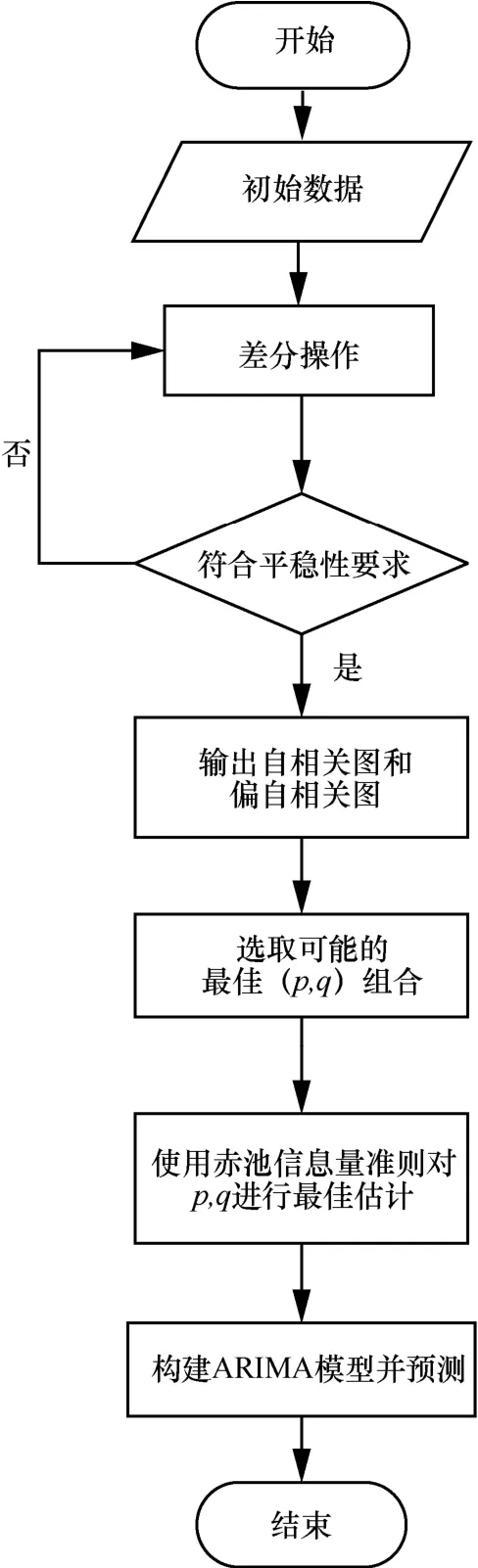
图1 ARIMA 模型预测流程
2.3 RNN 模型构建
1) RNN 隐藏层数
首先,RNN 与前馈神经网络(FNN,feedforward neural network)结构相似,具备与FNN 相似的数据拟合能力。其次,Hornik 等[18]已证明FNN 只需具备单个隐藏层和有限个神经元,即能较高精度地拟合任意复杂度的函数。因此本文将RNN 模型的隐藏层数设置为1。
2) RNN 输入层节点数
RNN 模型利用历史数据x(t−1),x(t−2),…,x(t−n)对x(t)进行预测(其中x(t)为时刻t的数据值,n为历史数据的个数)。因此,RNN 模型中输入层节点的数量由选取的历史数据个数决定。灰色关联分析法[19]是衡量序列数据相关程度的方法,灰色关联系数越大,则序列数据的相关性越强。本文采用灰色关联分析法,计算序列数据中每个数据与若干历史数据的平均相关性,确定与x(t)相关性较强的历史数据作为RNN 模型的输入,从而确定RNN 网络输入层节点个数,具体过程如算法1 所示。
算法1时间序列数据灰色关联分析法
输入经预处理的时间序列数据
输出时间序列数据中t时刻的值与历史值的平均相关系数

3) RNN 隐藏层节点数
本文采用经验法确定神经网络隐藏层节点数,经验法如式(2)所示。
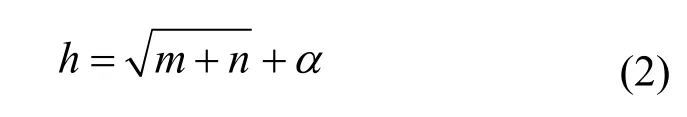
其中,h为RNN 模型中隐藏层神经元的个数,m为输入层神经元的个数,n为输出层神经元的个数,α∈{0≤x≤10,x∈Z} 。
2.4 ARIMA-RNN 组合模型构建及数据预测
ARIMA-RNN 组合模型的拓扑结构如图2 所示,预测过程如算法2 所示。ARIMA-RNN 组合模型的输入数据由两部分构成:ARIMA 模型对x(t)的预测值和x(t)的历史数据x(t−1),x(t−2),…,x(t−n)。RNN 模型训练过程中,误差函数采用均方误差(MSE,mean square error)函数,如式(3)所示。

图2 ARIMA-RNN 组合模型拓扑结构

其中,ytrue为实际输出,ypredictive为期望输出。
算法2ARIMA-RNN 组合模型预测算法
输入预处理的时间序列数据与ARIMA 模型预测值
输出预测结果
步骤1使用大小为m(m 步骤2将ARIMA 模型预测得到的数据通过式(1)映射到区间[−1,1]。 步骤3将步骤2 得到的序列数据截断,从第m个时刻开始取值,即α={αm,αm+1,…,αN},使截断后的ARIMA 预测数据与步骤1 的标签数据y={y m,ym+1,…,yN}相对应。 步骤4将步骤3 得到的数据加入步骤1 数据集的特征向量,得到Xt=[xt−1,xt−2,…,x t−m,αt],t=m,m+1,…,n,则ARIMA-RNN 模型的数据集为{Xt,yt|t=m,m+1,m+2,…,N}。 步骤5初始化RNN 各个权重矩阵和偏移向量的值。 步骤6计算数据集特征向量Xt在ARIMARNN 组合模型中的输出值。 步骤7依据式(3),计算步骤6 中得到预测序列与期望序列之间的误差,利用反向传播算法调整各个权重矩阵和偏移向量的值,使误差达到最小。 步骤8判断训练次数是否达到最大值或误差达到阈值,若是则保存调整好的权重矩阵和偏移向量,转步骤6 并输出预测结果;否则转至步骤7。 基于ARIMA-RNN 组合模型的云服务器老化预测方法在预测时间序列数据时,将ARIMA 模型的预测值和t−1,t−2,…,t−d时刻的历史数据作为RNN 模型的输入特征向量。首先通过ARIMA 模型对序列数据进行预测,ARIMA 模型预测方法的时间复杂度为O(n) ;然后将特征矩阵X(维度为[n,d])输入RNN 模型,与RNN 的隐藏层权重矩阵(维度为[d,w1])相乘,则时间复杂度为O(ndw1);最后将相乘结果与输出层权重矩阵(维度为[w1,1])相乘,则时间复杂度为O(nw1)。所以总的时间复杂度为 因此本文提出的ARIMA-RNN 组合模型的时间复杂度为O(n),即线性时间复杂度。 为探究基于OpenStack 云服务器的软件老化现象,实验中设计负载发生方案模拟云服务器的实际负载,并收集云服务器的资源和性能数据,作为研究软件老化的实验数据。通过对云服务器的资源和性能数据进行老化预测,为软件再生机制的部署提供理论依据。 本实验基于OpenStack 框架和QEMU/KVM 管理程序,实验系统由一台云服务器、一台MySQL数据库服务器及一组模拟客户端组成,如图3 所示。云服务器配置环境为Intel(R)Core(TM)i5-4590 CPU 四核3.3GHz、8GB RAM,操作系统为18.04.1-Ubuntux86_64,云服务器虚拟机上运行的操作系统为Redhat 7.3_64。云服务器端部署了一个基于Webbench 基准测试的Web 网站系统。在客户端编写负载脚本,依照Webbench 规范向云服务器发送网站商品查询的请求,同时监控并收集云服务器的性能参数和服务参数。实验以响应时间作为老化特征参数,实验样本数据为2 230 个,采样时间间隔为3 s。 图3 实验平台 首先,检验云服务器系统是否存在软件老化。响应时间的数据变化反映了云服务器系统运行性能表现状况,若响应时间随着系统运行时间的增长而增加,则可认定系统处于老化状态[20]。为了分析云服务器系统的老化状态,本文采用线性回归方法拟合响应时间数据的变化趋势,得到参数w=0.017,b=−0.71。原始序列数据和线性回归趋势如图4 所示,可以看出,云服务器在工作负载整体恒定的情况下,随着时间的推移,服务器的响应时间逐步上升,验证了云服务器出现软件老化现象。 图4 云服务器响应时间数据趋势 其次,实验中应用ARIMA-RNN 组合模型进行预测,将响应时间数据集划分为训练集和测试集(其中训练集为前80%的数据集,测试集为后20%的数据集)。采用组合模型进行二步老化预测,第一步采用ARIMA 模型对响应时间t时刻的数据值做出预测,第二步将ARIMA 模型预测结果值和t时刻之前的响应时间数据一并输入到RNN 模型,得到响应时间t时刻的最终预测值。 用ARIMA 模型对响应时间预测时,首先,采用单位根检验方法,对响应时间的序列数据进行平稳性检验,确定ARIMA 模型中参数d的值。经过一次差分处理后,单位根检验结果如表1 所示。表1中统计量值为−20.567 5,小于3 个置信度(1%,5%,10%)的临界统计值,P=0,表示拒绝原假设,因此ARIMA 模型差分系数d=1。 表1 单位根检验结果 其次,通过偏自相关和自相关分析,确定自回归项p和移动平均项q的取值范围。如图5 所示,偏自相关分析显示滞后阶数为1~12 阶时,偏自相关系数超出了置信边界,滞后阶数大于12 阶后偏自相关系数缩小至接近0。自相关分析显示滞后阶数大于5 阶后,自相关系数处于置信区间。因此p的值可能为11 或12,q的值可能为5 或7。 图5 偏自相关和自相关分析 最后,依据AIC 准则对待选参数p和q进行最佳估计。将响应时间数据作为输入,用p和q的可能值构建ARIMA 模型,分别计算模型对应的AIC值,如表2 所示。可以看出,ARIMA(12,1,7)的AIC值最小,因此,选择ARIMA(12,1,7)模型对响应时间进行预测,预测结果如图6 所示。 表2 ARIMA 模型的AIC 值 此外,图7 给出了响应时间实际值的变化率,即响应时间随时间序列数据的斜率变化曲线,其值越大表示响应时间变化越明显。时间序列数据为0~500 时,响应时间变化率较小,表明该段序列数据变化较为平缓;时间序列数据为1 000~1 500 时,响应时间变化率较大,表明该段序列数据变化剧烈。图8 给出了ARIMA 模型对响应时间进行预测的绝对误差。可以看出,波动平缓的数据(时间序列数据为0~500)预测绝对误差较小,而波动剧烈的数据(时间序列数据1 000~1 500)预测绝对误差较大。因此,可以判断对于波动剧烈的时间序列数据,用ARIMA 模型预测效果较差。 图6 ARIMA 模型预测结果 图7 响应时间实际值的变化率 图8 响应时间预测绝对误差 综上,由于云服务器系统性能数据和资源数据具有突发性、变化剧烈以及周期性的特点,对于变化剧烈的时间序列数据,用ARIMA 模型预测效果较差。因此仅采用单一的ARIMA 模型对云服务器进行老化预测,效果并不理想。 构建ARIMA-RNN 组合模型,需确定RNN 网络结构。首先,采用算法1 计算响应时间序列数据的相关性,如图9 所示,平均相关系数呈波动下降的趋势,当历史数据个数为10 时数据的相关性最强,因此ARIMA-RNN 组合模型的输入层节点数为10。然后,根据式(2)得到隐藏层节点数的最佳取值区间,并经过反复实验测试,得到隐藏层节点数最优值为20。此外,本实验RNN 网络中激活函数选取tanh 函数,该函数值域为[−1,1],对于特征相差大的数据处理效果较好。 图9 响应时间序列数据的相关性 然后,使用ARIMA-RNN 组合模型、ARIMA模型[21]以及RNN 模型[22]对响应时间进行预测,预测结果如图 10(a)所示。训练数据集区间为[0,1784],测试数据集区间为[1 785,2 230]。由于数据量大且数据变化较为剧烈,为了显示清晰每隔50 个数据点输出结果。可以看出,ARIMARNN 组合模型拟合效果最好。3 种模型的预测结果误差对比情况,如图10(b)所示。可见ARIMA模型和RNN 模型各有优势,在数据较平稳的区间数据,如0~500 区间数据,ARIMA 模型的预测精度优于RNN 模型预测精度;而在数据波动较为剧烈的区间数据,如1 500~2 000 区间数据,RNN 模型预测精度优于 ARIMA 模型。ARIMA-RNN 组合模型结合了这两者的优势,预测精度最高。 本文从预测精度、预测收敛速度及可扩展性3 个方面,对本文所提预测方法进行性能评价。首先,在评判算法预测精度方面,采用均方根误差RMSE、平均绝对误差MAE 及平均绝对百分比误差MAPE作为评价指标,计算式如下所示。 其中,n为数据样本的个数,ypredictive为预测序列数据,ytrue为实际序列数据。 图10 响应时间预测及误差对比 使用ARIMA-RNN 组合模型、ARIMA 模型[21]和RNN 模型[22],对响应时间数据进行预测精度对比,如表3 所示。ARIMA-RNN 组合模型的RMSE、MAE 和MAPE 值均最小,其次是RNN模型,ARIMA 模型预测误差最大。而ARIMA-RNN 组合模型相较ARIMA 模型和RNN模型,RMSE 分别降低了83.90%和76.61%,MAE分别降低了86.10%和74.24%,MAPE 分别降低了81.23%和71.47%。可见,本文所提ARIMA-RNN组合模型,在预测云服务器性能数据时比ARIMA模型和RNN 模型的预测精度更高。原因是本文针对OpenStack 云服务器的系统性能参数在运行时的数据变化特点,设计ARIMA-RNN 组合模型进行系统老化预测,克服了ARIMA 模型对于波动较大数据预测精度较低的局限性,因而提高了预测精度。 表3 各模型误差对比 其次,在评价预测收敛速度方面,将本文所提的ARIMA-RNN组合模型与RNN模型进行了对比,网络训练过程的收敛趋势如图11 所示。本文基于ARIMA-RNN 组合模型的预测方法,在模型训练过程中,当训练次数为10 时,均方误差MSE 值已小于0.0015,之后收敛趋于稳定,相较RNN 模型预测方法,本文基于ARIMA-RNN 组合模型的预测方法收敛速度更快且误差更小。原因是本文预测方法在RNN 网络训练前,采用灰色关联分析方法,将相关性分析后的时间序列数据作为模型输入再进行预测,减少了相关性较差数据的输入,从而提高了预测收敛速度。 图11 模型训练收敛趋势对比 最后,在评价预测方法的可扩展性方面,使用ARIMA-RNN 组合模型、ARIMA 模型和RNN 模型,对云服务器的CPU 使用率时间序列进行预测并对比,如图 12 所示。从图 12 可以看出,本文ARIMA-RNN 组合模型,较单一的ARIMA 模型和RNN 模型,具有更好的预测效果。 图12 CPU 使用率预测及误差对比 综上,云服务器处于动态变化的复杂环境中,系统性能参数的时间序列波动变化,本文针对数据波动平缓和剧烈2 种情况,结合ARIMA 模型和RNN 模型,预测云服务器系统的老化趋势,预测精度更高,同时,采用灰色关联度分析法,计算时间序列数据的相关性,预测收敛速度更快。 软件老化问题一直受到学术界和工业界的关注。软件老化预测及分析可以保障云服务器系统可靠运行,降低系统风险和损失。针对收集到的OpenStack云服务器性能数据,本文提出一种基于ARIMARNN 组合模型的预测方法,对云服务器的性能资源进行老化预测,并验证了软件老化现象的存在。实验结果表明,ARIMA-RNN 组合模型提高了预测精度和收敛速度,为云服务器再生部署提供了参考依据。 下一步将研究预测模型对于数据变化情况下的敏感性问题,使数据出现急剧变化时,仍能获得较为精确的预测结果。2.5 时间复杂度分析

3 实验结果与分析


3.1 ARIMA 模型预测结果及分析




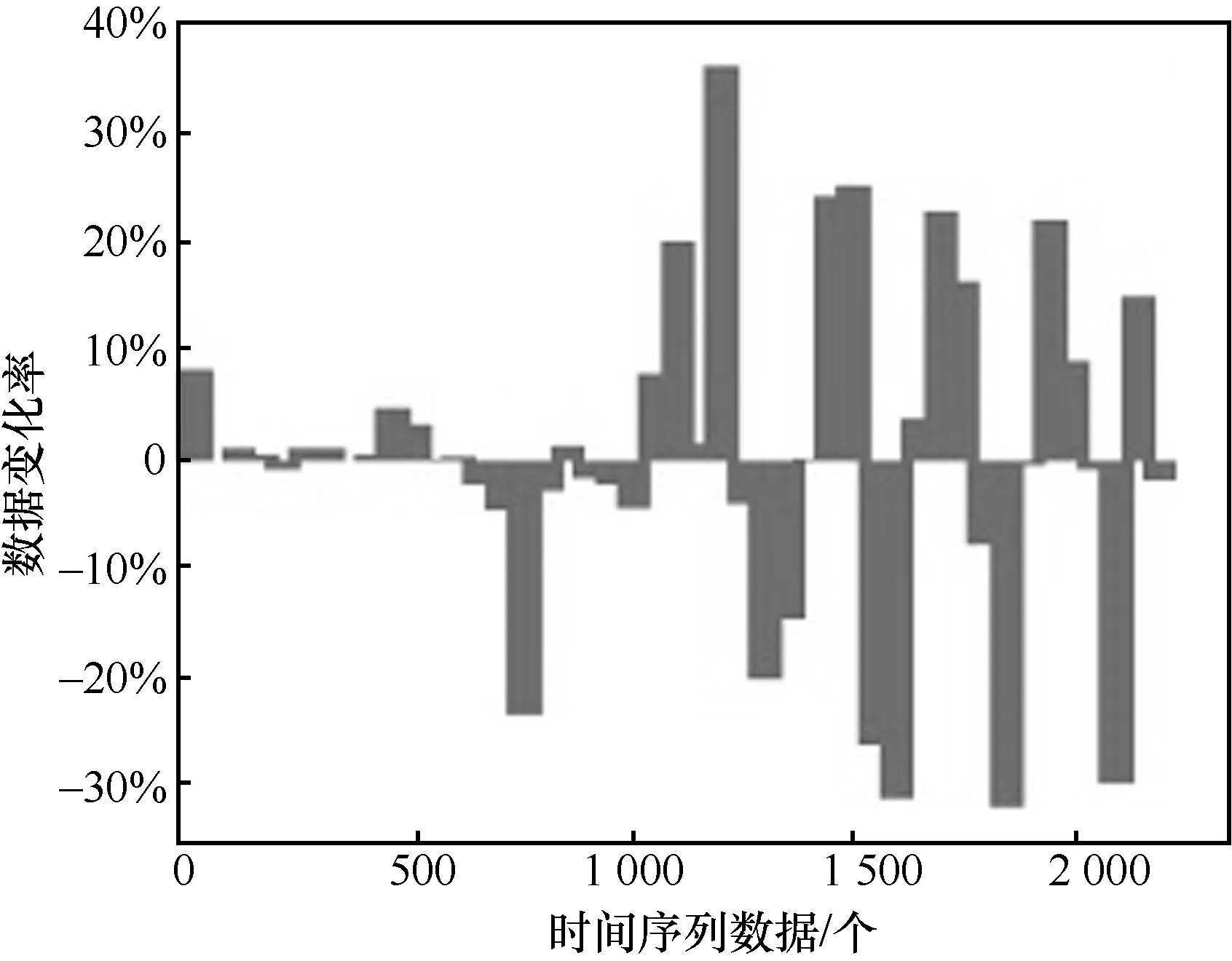

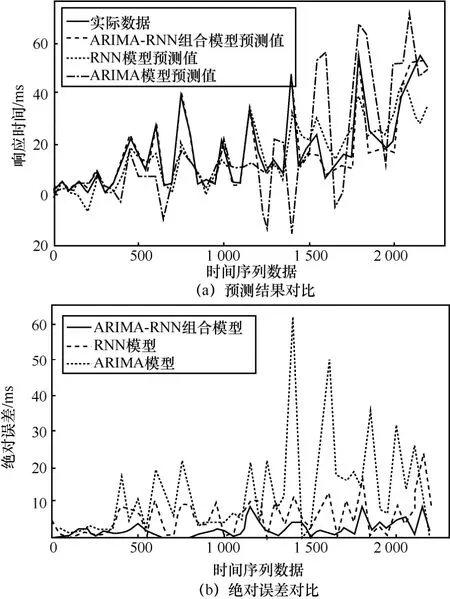
3.2 ARIMA-RNN 组合模型预测结果及分析

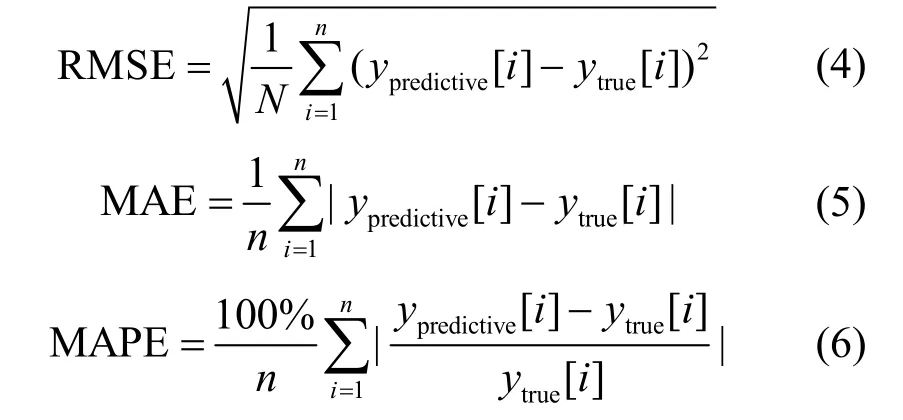
3.3 预测性能评价



4 结束语

