制造云服务组合中支持服务关联的QoS感知评估模型

谢晓兰，曾兰英，翟青海

（1.桂林理工大学广西嵌入式技术与智能系统重点实验室，广西 桂林 541004；2.桂林理工大学信息科学与工程学院，广西 桂林 541004）

1 引言

随着制造业的发展，传统制造模式难以满足客户复杂多样的需求，制造资源和制造能力未能有效利用，以至于不少制造企业面临资源瓶颈和资源闲置问题[1]。基于此，李伯虎院士提出了“云制造”的概念[2]，将制造云平台作为云制造系统的中间媒介连接用户和服务提供商，改变了制造资源和制造能力的流通方式。但由于制造规模扩张，单一的服务资源不能完成复杂的制造任务，因此需将制造云平台中具有不同功能的制造资源服务以组合的方式形成随需求即时变换的松耦合制造云服务应用，从而满足整个制造生命周期中的各个功能需求[3]。

服务质量（QoS,quantity of service）作为衡量服务组合好坏的非功能需求指标，是制造云服务组合的重要筛选方式。在满足功能需求的情况下，如何从海量功能相似但QoS 不同的制造云服务中挑选出较好的服务组合是首要问题[4]。通常采用建立QoS 评估模型并结合群体智能算法等优选方式进行问题求解，得到最佳服务组合。

陈友玲等[5]建立了服务需求方和服务提供商的双侧约束，通过服务质量计算模型对制造云服务组合进行综合评估，并采用改进的i-NSGA-II-JG 算法进行求解。Lu 等[6]提出了一种利用分布式知识进行制造云服务能力评估和推荐的系统框架，并基于Web 的系统形式实现了该方案。Afshin 等[7]提出了一种基于Agent 的混合方式实现服务组合，通过识别QoS 参数和粒子群算法来选择优质服务，提升了组合资源和等待时间方面的性能。Li 等[8-9]考虑了服务调用顺序以及服务之间的时间关系，以资源服务链的方式对服务顺序组合进行描述，并提出了资源服务链组成算法进行方案求解。

以上关于制造云服务组合的研究大部分都是在基于服务独立、不存在任何依赖关系的前提下展开的，但在实际制造生产工作流程中，制造云服务之间或多或少存在各种关联关系，如接口关联（InC,interface correlation）、业务实体关联（BuC,business-entity correlation）和统计关联（StC,statistical correlation）等。若忽略实际制造过程中关联关系对QoS 的影响，会过滤掉一些较好的服务组合方案。

有不少学者对服务关联进行了探索。Tao 等[10]着重研究了2 个服务间的商业实体关联关系，并阐述了相应的QoS 描述模型。Lina[11-12]在分析服务间存在关联的基础上，研究了一种剔除冗余服务的服务选择方法，提高了选择效率。Xu 等[13]和田思思等[14]建立了基于关联关系的云制造服务聚合模型（CMSA-CA,correlation aware cloud manufacturing service aggregation），并采用改进的离散蜂群算法（IDBA-Pareto,improved discrete bees algorithm based on Pareto）得到非劣服务组合解集。Liu 等[15]建立了含有3 种关联的综合QoS 相关性模型，并基于该模型应用了基于案例库的并行最大最小蚂蚁系统（PMMAS-CL,parallel max-min ant system based on case library）算法求解。

以上研究对服务组合关联的QoS 感知时效性未能有良好体现，因此本文在前人的基础上进一步对业务实体关联和统计关联进行研究，提出了支持服务关联的QoS 感知评估模型。在业务实体关联中考虑了服务提供商的合作时长，有效区分企业合作的好坏。在统计关联中充分挖掘服务组合历史记录信息，利用“分时有效”的思想预测得到当前时间的QoS，并结合关联规则评估中相关性度量参数KULC（kulczynski）和不平衡因子（IR,imbalance ratio）[16]形成动态变化量以保证统计关联的时效性。最后建立了多目标优化模型，使用含有关联分析的NSGAII（non-dominated sorting genetic algorithm II）进行求解，筛选出了制造云环境下较优质的服务组合解集。本文的主要工作和贡献如下。

1) 主要分析了业务实体关联和统计关联，并提出了相应的服务描述模型和计算方式。将企业合作时间引入业务实体关联中区分合作优劣；在统计关联中，利用关联规则相关性度量参数KULC 和IR评估服务组合的关联强度，并结合时间衰减函数得到的QoS 预测值动态调整统计关联的QoS 变化量，使服务组合QoS 更能贴合实际制造环境。

2) 建立了支持服务关联的QoS 感知评估模型，并利用基于Pareto 最优解的NSGAII 多目标优化算法进行问题求解。将服务关联分析引入算法中，通过全局约束进行寻优限制，得到非劣服务组合解集，有助于服务需求方做出更合理的决策。

2 问题描述与模型介绍

2.1 制造云服务组合流程

在给出定义之前，对所涉及的部分符号表示及含义进行说明，如表1 所示。

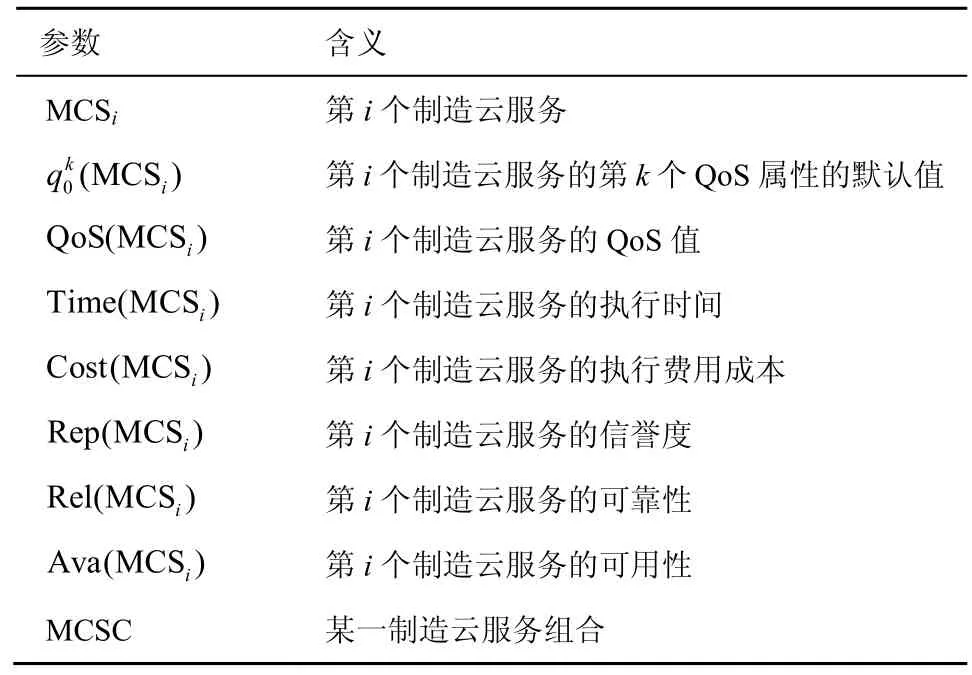
表1 符号表示与含义

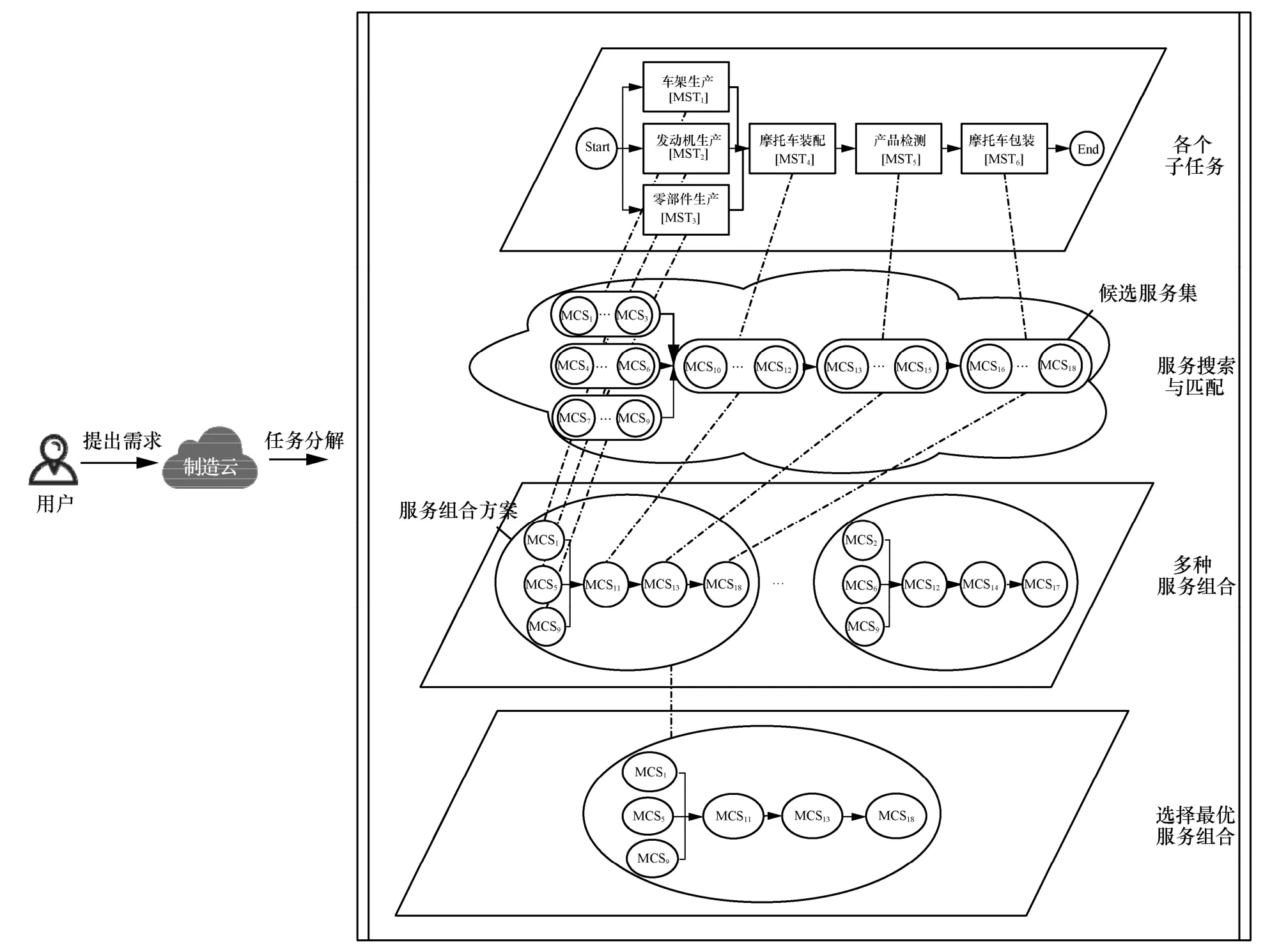
图1 制造云服务组合流程

以摩托车生产装配过程这一实际应用场景为例，如图1 所示，用户提出装配任务后，首先对服务组合进行设计，将制造任务（MT,manufacturing task）分解成6 个制造子任务（MST,manufacturing subtask），分别是车架生产MST1、发动机生产MST2、零部件生产MST3、摩托车装配MST4、产品检测MST5、摩托车包装MST6。然后对制造子任务的功能和流程进行分析，形成抽象的服务组合执行路径。在服务组合部署阶段，分别按照每个子任务的功能需求在制造云平台中对服务进行搜索与匹配形成候选服务集（如MCS1、MCS2等），并通过QoS 评估模型从候选服务集中选出对应的单个制造云服务（MCS,manufacturing cloud service）形成多种组合方案。最后从中选择优质的服务组合即为最终服务组合执行路径。

2.2 制造云服务描述模型

在制造云平台中，首先根据服务提供商所提供的服务进行基本信息描述完成云服务的注册建模，发布到云服务资源池中供用户使用。基于服务的网络本体语言（OWL-S,ontology Web language for service）对制造云服务的语义描述提供了良好的支持，不少学者在此基础上对其进行了形式化描述。本文引入了文献[17-18]中含有关联关系的形式化描述方式，将制造云服务MCS 建模为一个六元组，如式(1)所示。

其中，MCSbasic为制造云服务的基本信息，如名称、参数等；MCScategory为制造云服务类别，如制造资源、制造能力和制造知识；MCSstatus为制造云服务的状态信息，如空闲、未满负荷、满负荷和超负荷等；MCSfunction为制造云服务的功能描述，如输入、输出等；MCSQoS为制造云服务的服务质量QoS，是选择选择服务并评估服务组合好坏的标准；MCScorrelation为制造云服务间的关联关系，如接口关联、业务实体关联和统计关联等。

3 制造云服务关联模型

制造云服务描述模型中 MCScorrelation包含接口关联、业务实体关联和统计关联3 种服务关联关系，下面将给出相应的定义、描述模型和QoS 计算方式。

3.1 服务关联关系

3.1.1 接口关联

定义1接口关联。在制造云服务组合过程中，MCSi为MCSj的前驱服务，MCSj为MCSi的后继服务。MCSi的输出与MCSj的输入之间的数据逻辑关系即为接口关联。制造云服务的接口关联可以用式(2)描述。

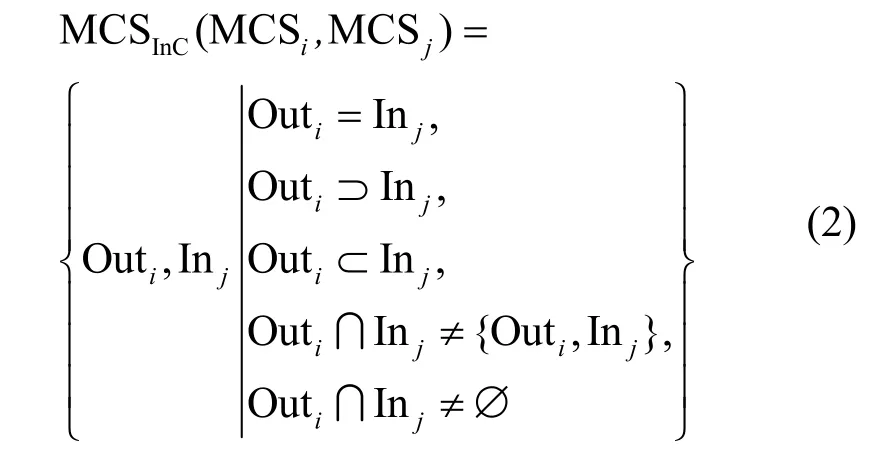
其中，Outi是MCSi的输出，Inj是MCSj的输入。接口关联关系可分为5 类，在式(2)中从上至下依次为等价匹配、完全匹配、部分匹配、交叉匹配、无关联匹配。在摩托车生产装配流程中，假设车架生产采用的服务为MCS1，摩托车装配选择服务为MCS10，则可以表示为

由于车架生产的输出是摩托车装配输入中的一部分，即为部分匹配。在接口关联中MCSi的QoS各属性的计算式可表示为

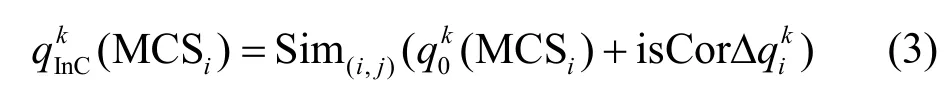
其中，Sim(i,j)表示MCSi和MCSj的接口关联度，即输入输出的语义相似度，一般从概念、属性和属性值3个维度进行度量；isCor 表示MCSi与MCSj之间是否存在接口关联，其值为0（表示不存在）或1（表示存在）。

3.1.2 业务实体关联

定义2业务实体关联。在制造云服务平台中，不同云服务提供商之间的企业利益关系，即合作或竞争。业务实体关联一般用四元组进行表示，如式(4)所示。

其中，δ表示MCSj与MCSi之间是否存在业务实体关联关系，其值为0 或1。

3.1.3 统计关联

定义3统计关联。制造云平台中，2 个或多个云服务经常被绑定应用于同一服务组合中执行某一制造任务。统计关联常用三元组进行表示，如式(6)所示。

其中，γ为MCSi与MCSj历史合作执行成功次数；E为MCSi与MCSj历史合作总次数，包含了任务执行失败情况。式(7)即为服务组合被绑定执行效果好坏的评价标准。

统计关联主要影响制造云服务QoS 中时间、信誉度、可用性和可靠性4 个属性值[17-18]，其MCSi的QoS 属性计算式可表示为

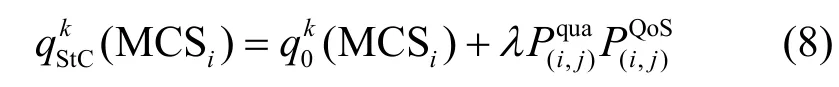
其中，λ表示MCSi与MCSj是否存在统计关联关系，其值为0 或1。

式(3)、式(5)和式(8)可将服务之间的关联关系直接作用于QoS，通过建立基本的QoS 评估模型对服务进行选择。

3.2 基本QoS 评估模型

本文主要将QoS 中时间（Time）、成本（Cost）、信誉度（Reputation）、可用性（Availability）、可靠性（Reliability）这5 个属性作为QoS 评估指标，单个制造云服务QoS 可形式化表示为

制造云服务组合的抽象工作流中包含了一种或多种逻辑控制结构，如顺序结构、并行结构、选择结构和循环结构。不同逻辑控制结构的计算方式也有所不同，一般计算服务组合的QoS 会将非顺序结构转换为顺序结构进行计算。本文只讨论顺序结构，服务组合的QoS 各属性可通过单个服务QoS 累加、累乘或求平均的方式计算得到，如式(12)所示。

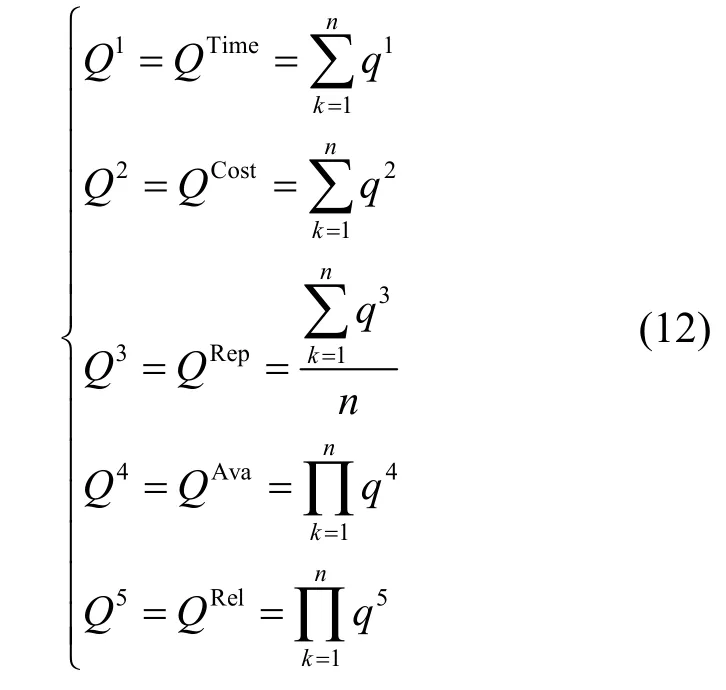
其中，Q1～Q5分别表示服务组合QoS 中时间、成本、信誉度、可用性、可靠性5 个属性，n表示服务组合中含单个服务的数量。综合考虑以上属性，则某一制造任务的服务组合 QoS 综合评估值Q(MCSC)的计算式为

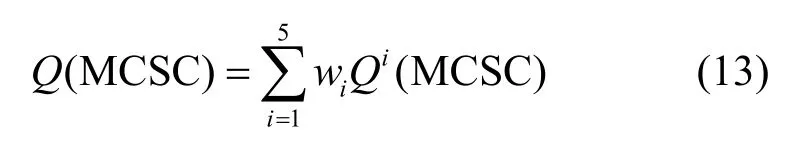
其中，wi为第i个QoS 属性的权重，一般是服务需求方设置，反映各属性的优先顺序；Qi(MCSC)为服务组合第i个属性值。

4 支持服务关联的QoS 感知模型与求解

4.1 支持服务关联的QoS 感知模型

本文根据制造云服务的特点改进了服务组合关联模型中业务实体关联和统计关联，考虑了企业合作时长和历史服务组合情况，提出了合作时间因子和基于预测的QoS 变化量，在保证满足制造任务的同时，最大化服务组合QoS 水平，提升服务组合的时效性。

4.1.1 合作时间因子

制造云平台中云服务提供商往往会建立合作关系以达到共赢目的。建立长期的合作关系，不仅可以充分利用双方资源，还能更快、更好地实现制造企业降低成本、缩短产品生产周期等战略目标。合作时间越长，企业之间工作接洽越协调，合作效果越好；反之，合作时间越短，越容易出现一些合作问题与风险。

介于上述情况，本文从制造云服务描述模型中提取出提供商之间合作时间，并对合作时间进行归一化处理形成时间因子融入业务实体关联模型中，即将业务实体关联中MCSi的QoS 属性计算式(5)调整为

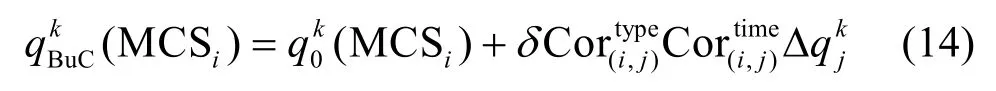
同时，将业务关联中合作关系、无关系、竞争关系量化表示2、1、0.5 分别调整为1、0、−1，使竞争关系差量增大，即增加了竞争关系的惩罚。

4.1.2 基于预测的QoS 变化量

在统计关联中，之前的研究简单地通过服务组合执行制造任务的成功次数与总执行次数的比例来衡量统计关联的好坏，忽略了2 个服务形成的关联规则的影响。此外，统计关联中QoS 变化量常为人工随机赋值且固定不变，缺乏客观实际性和动态性，难以发现2 个服务在近一段时间内组合执行制造任务的效果。针对上述问题，本文考虑了时间因素并结合相关性度量参数KULC 和IR 动态生成统计关联的QoS 变化量。在式(6)的基础上调整了统计关联的描述模型，如式(15)所示。

将KULC 和IR 相结合作为2 个服务之间关联规则的评估指标，是对关联强度的良好度量方式[16]。KULC 表示MCSi和MCSj的相关性，当KULC≥0.7时，即MCSi的出现促进了MCSj的出现，称为正相关；当KULC≤0.3 时，称为负相关。KULC 对双向置信度做了一个良好的平均，有效避免了由于历史记录数据的数值大小对关联规则可靠性造成的影响。IR 度量了双向关联规则是否平衡，若IR 越接近0，则表明MCSi和MCSj之间的关联规则越平衡，对于双方出现的可能性相同。一般IR≤0.3 为平衡，IR≥0.6 为不平衡。

为了保证制造云服务的QoS 能够更加贴合实际服务质量信息，受文献[19]的启发，在基于服务组合历史记录进行QoS 值预测时，采用了“分时有效”的思想，根据历史记录的时间信息对QoS 进行加权计算，距离越近权重越大，即越可靠，距离越远权重越小，即可靠性越差。这样预测得到的QoS更具时效性，也更能反映出近阶段2 个云服务组合执行制造任务时的服务质量状态。的具体计算过程如下。

首先，利用时间衰减函数计算MCSi和MCSj每条历史组合记录信息的时间系数β，即历史记录的参考程度。假设有m个时间，每一个时间的时间系数的计算式为

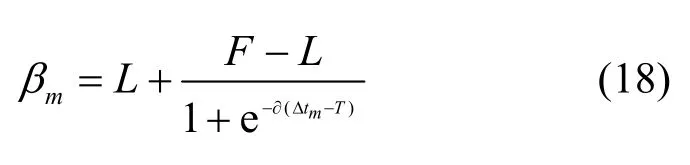
其中，L表示距离最近的时间的权重，F表示距离最远的时间的权重，∂表示权重增长率，T表示最大权重所处的时间段。

然后，将时间系数β进行归一化处理，使MCSi和MCSj历史组合记录的时间权重之和为1。最后，加权融合得到QoS 预测值。

针对所提出的统计关联描述模型，其对应MCSi的QoS 属性计算式为

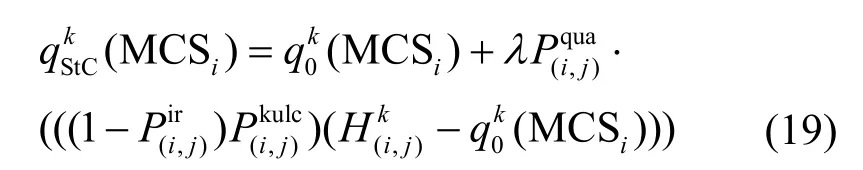
服务组合历史记录信息在不同时间内含有的记录个数不同，并且相同服务组合在不同时间的执行效果不一，则QoS 预测值以及KULC 和IR 会随时间波动，从而使云服务QoS 变化量动态调整。这样不仅能保证统计关联的时效性，还可以对制造云服务统计关联有良好的区分。

4.2 模型求解

QoS 属性中有增量和减量2 种类型，如成本、时间，其值越小，表示服务质量越好；再如可靠性、可用性和信誉度，其值越大，表示服务质量越好。因此，在计算服务组合加权QoS 前，需要对QoS属性进行无量纲化处理，如式(20)和式(21)所示。

制造云服务组合本质上是由一系列候选云服务按照制造工艺流程构成的执行路径。在基于QoS对制造云服务组合优选时，需要平衡QoS 中如时间、成本等不同属性之间的性能。目前，大部分研究采用线性加权等方式将多目标转换为单目标进行求解，所得到的解较单一，不能有效解决多个子目标带来的冲突，并且权重依赖过大，主观性过强。

因此，本文将采用基于Pareto 最优的多目标优化对服务组合问题建模，将制造时间、制造成本作为2 个子目标进行求解，模型如式(22)和式(23)所示。

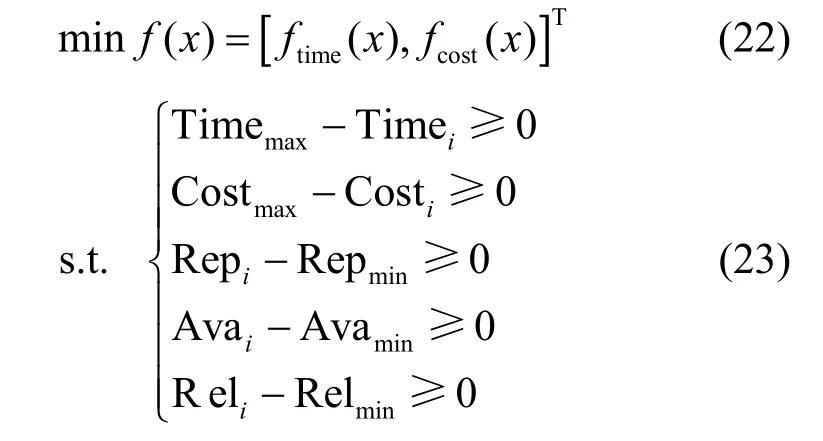
其中，式(22)为需要优化的目标函数，本文将时间和成本作为制造云服务组合中的主要冲突目标，尽可能使制造时间和制造成本最小化；式(23)为全局约束，制造云服务组合的时间和成本不能高于服务需求方制定的最大可接受值，信誉度、可用性和可靠性不能低于服务需求方的最低期望值。

本文采用了多目标优化中经典的NSGAII[20]对所建模型求解。其算法的主要思想如下。一个解集中由于需要同时优化多个目标函数值，则无法保证每个目标函数都能取得最优解，使某些解之间目标冲突，导致无法进行比较，对此可利用非支配排序的方式。首先，对解集中的解进行两两比较，若不存在任何一个解优于解xi，则xi为非支配解即Pareto 解，找出所有Pareto 解为第一级非支配层，将剩余支配解按照上述流程找出新的Pareto 解为下一级非支配层。如此循环，将解集进行分层，得到每个解的层级即Rank，使每一层内的解均为Pareto解。同时，计算每个解的拥挤度D，即衡量解集多样性指标，通过Rank 和D区分解的优劣情况。最后结合遗传操作和精英选择策略，经过不断迭代后，筛选出Pareto 最优解集即非劣服务组合解集。

一个服务组合就是一个解也称为个体，n个个体的集合即为一个种群。在NSGAII 中，个体采用实数编码，其编码位置的数值为对应子任务选择的服务编号，如服务组合[2,11,20,32,40]即第一个子任务选择2 号制造云服务依次类推。将关联分析流程引入NSGAII 中，对种群中每个个体进行3 种关联关系分析，并返回个体的各个目标函数值，最后择优选择，具体流程如图2 所示。

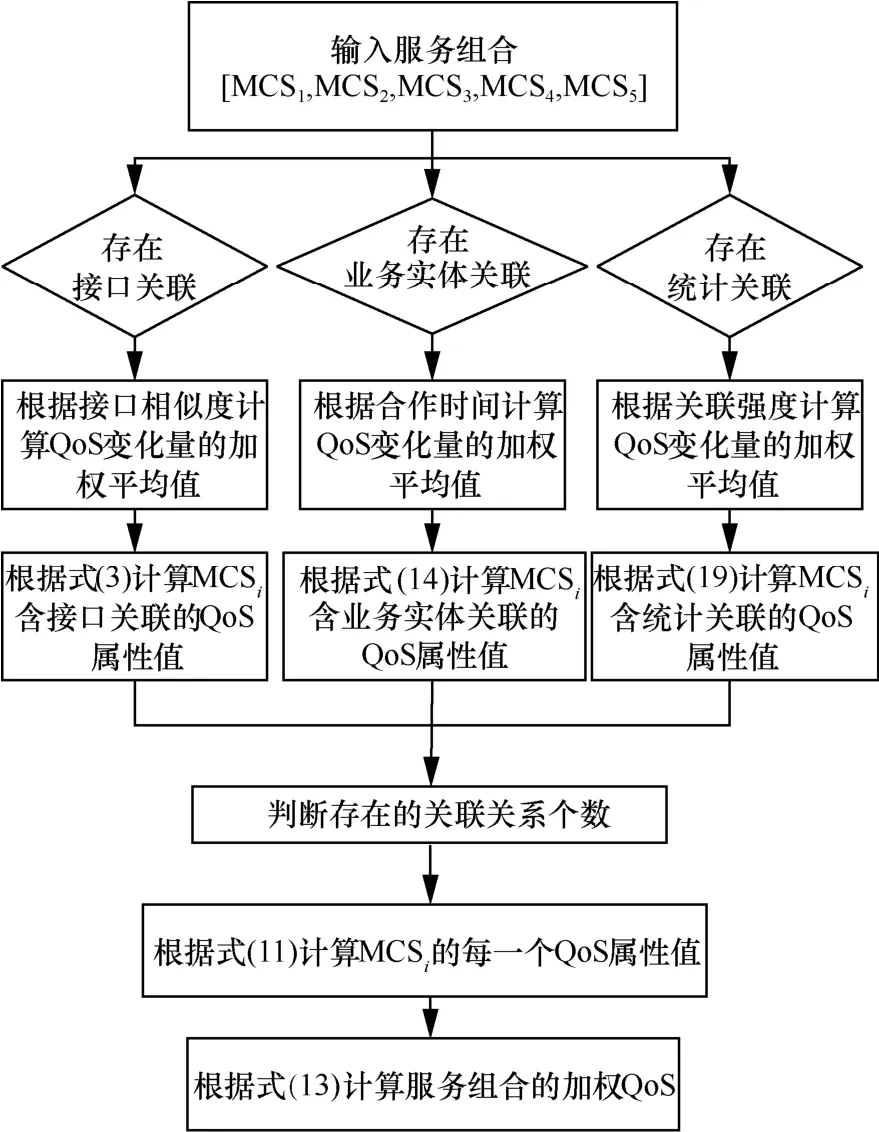
图2 服务关联分析流程

具体算法流程介绍如下。

步骤1随机生成规模为n的初始化种群Pt，对种群进行关联分析，返回目标函数值。

步骤2对种群Pt进行非支配排序，形成非支配集Z，并初始化每个个体的Rank 值。

步骤3进行遗传操作（选择、交叉、变异），产生第一代子代种群Qt。

步骤4合并种群Pt和Qt，形成组合种群Rt=Pt+Qt。

步骤5对Rt进行快速非支配排序，计算出每个支配层的个体拥挤度，结合精英选择策略选出n个个体形成性的父代种群Pt+1。

步骤6满足最大迭代次数，得到Pareto 最优解集合；反之，返回步骤2。

5 实验与结果分析

本节通过算例实验以及与文献[15]的对比分析，验证本文所提模型的可行性和有效性，并以服务组合排名和QoS 变化情况说明引入合作时间因子和采用基于预测的QoS 变化量对服务组合选择的时效性影响。

5.1 实验设计

假设制造云平台中有15 个服务提供商，每个服务提供商有3 种不同类型的制造云服务，共45个制造云服务。现有一制造任务被分解为由5 个子任务串联组成的业务流程，如图3 所示，每个子任务有3 个服务提供商可提供相应需求的制造云服务，即每个子任务有9 个候选云服务。

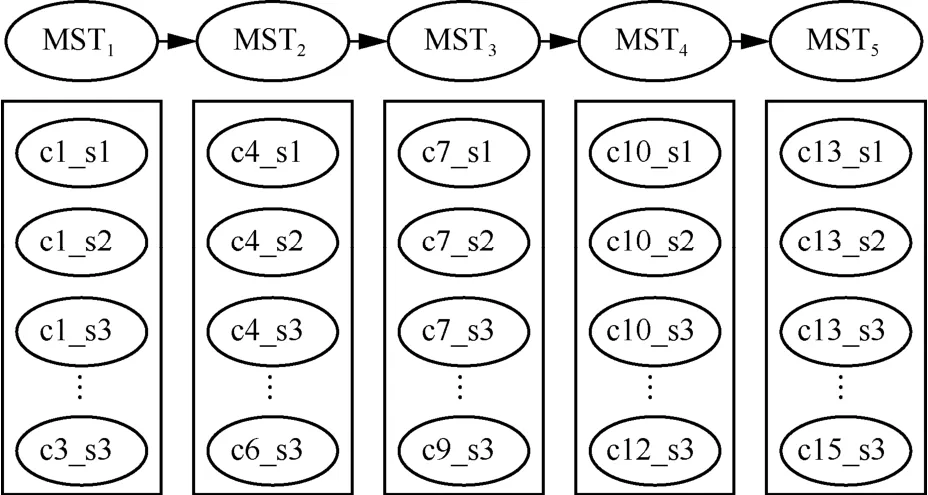
图3 制造子任务流程

1) 实验数据

按照传统制造业企业的典型运作方式，本文将制造工作流程简化为设计、采购、生产、质检、配送，并分别对应上述划分的5 个子任务。为保证实验数据的科学性、推测性和一般性，参考了前人实验数据设定并结合制造流程中各子任务制造时间和制造成本的不同，按照如表2 所示的不同数值范围随机生成了候选服务的QoS。

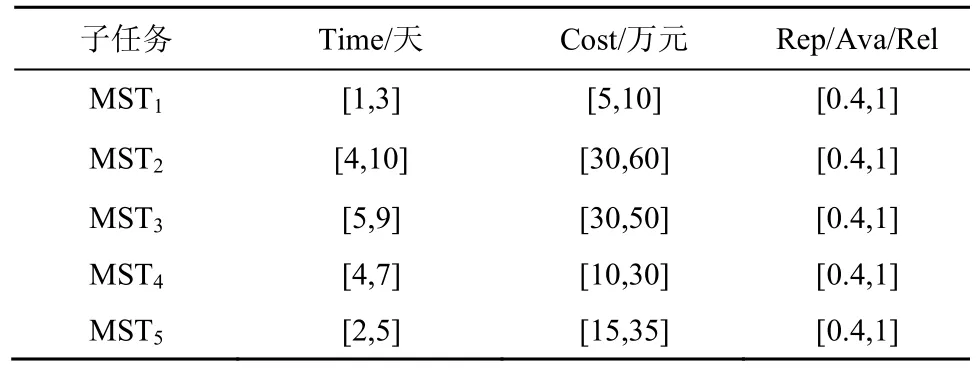
表2 制造云服务QoS 取值范围

在接口关联关系中，相似度Sim 的取值范围为[0.7,1]。在业务实体关联关系中，随机选择一定比例的服务提供商形成合作或竞争关系，并随机生成数值范围为[1,10]的合作时间。通过多次模拟实验，生成1 000 条历史服务组合记录。

2) 实验参数设置

3 种关联关系权重ω分别为[0.2,0.4,0.4]；关联规则选取中支持度为所有支持度的均值，置信度为所有置信度的均值；NSGAII 中交叉率为0.9，变异率为0.3。

3) 实验方案

为检验所提服务关联QoS 感知模型的可行性和有效性以及关联关系中关联比例和历史记录的影响，基于表3 中的制造需求参数，本文设计了3 组实验，每组实验将分别独立运行30 次并取平均结果进行对比。

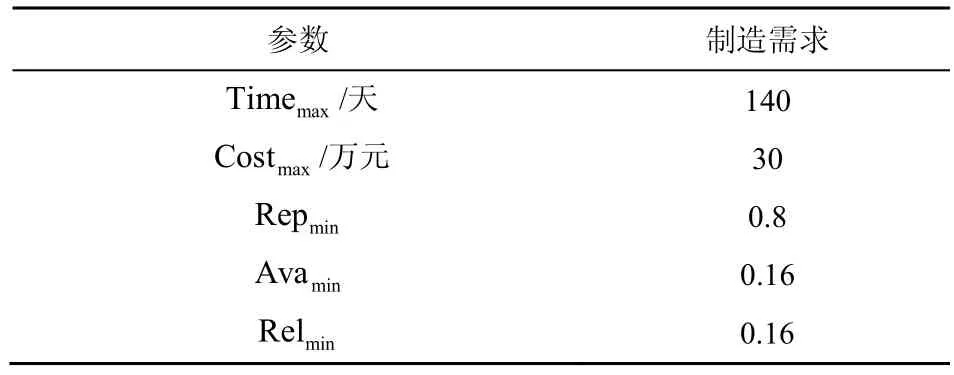
表3 制造需求参数设置

5.2 服务关联QoS 感知模型的验证（实验1）

指定业务实体关联比例为20%，当前时间为2020 年8 月1 日，分别按照迭代次数为200、400、600、800 开展实验。

如图4 和图5 所示，以时间和成本作为服务组合的关键性能指标，含关联分析的服务组合平均时间和成本均小于不含关联分析的情况。从时间上看，含关联分析的服务组合平均时间约为22～23 天，不含关联分析的服务组合平均时间约为26～27 天，相差约为4 天；从成本上看，含关联分析的服务组合平均成本约为117～119 万元，不含关联分析的服务组合平均成本约为123～124 万元，相差约6 万元。可见，服务关联降低了制造成本、缩短了制造时间，为服务需求方带来效率和收益上的提升。

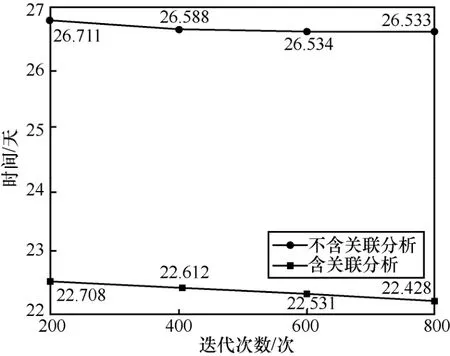
图4 不含关联分析与含关联分析的时间对比

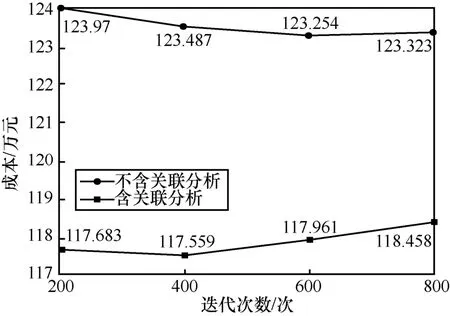
图5 不含关联分析与含关联分析的成本对比

为了体现本文所提模型对制造云服务组合评估的显著效果，使用不含关联分析方法和文献[15]中含关联的QoS 模型与本文所提模型进行对比实验。

假设服务需求方设置的QoS 属性权重wi分别为[0.3,0.3,0.2,0.2,0.2]，在随机生成的模拟数据上，直接采用式(12)计算QoS 各属性值，再使用式(13)计算得到不含关联分析时服务组合的加权QoS1。并将不含关联分析的服务组合集合进行非支配排序，取排名前10 的服务组合（如表4 所示）作为对比验证的服务组合方案。再以文献[15]的计算方式得到加权QoS2；按照图2 中关联分析流程求解得到加权QoS3。最终3 种方式计算得到的加权QoS 对比分析如图6 所示，并呈现如表5 所示的变化。

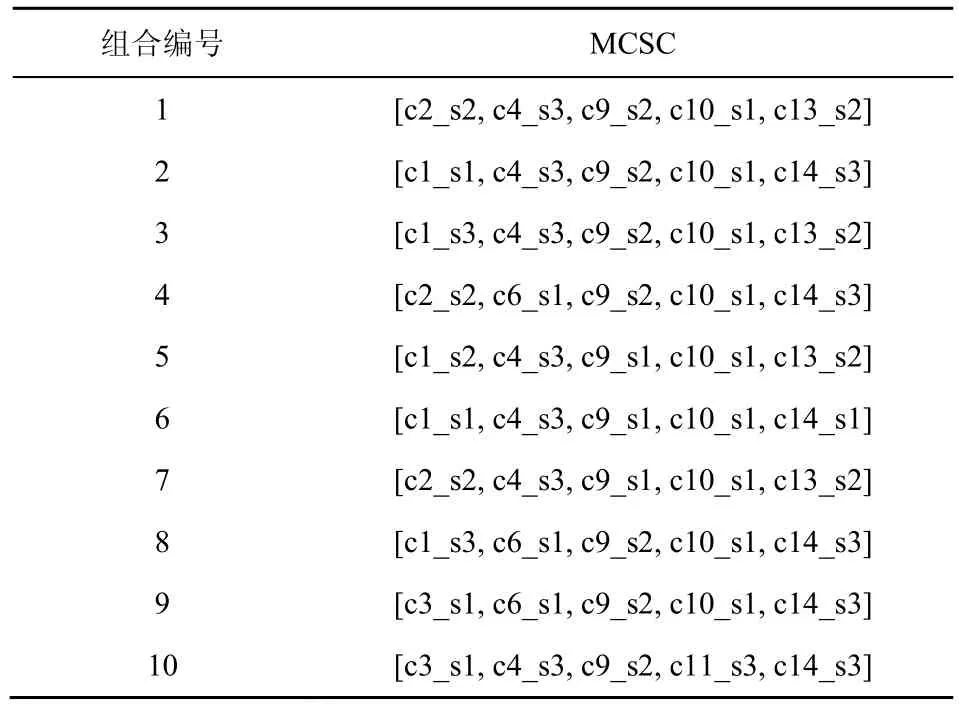
表4 服务组合编号及方案

如图6 所示，对于相同的服务组合而言，经过关联分析后服务组合的加权QoS 都呈现大幅度变化，含服务关联分析的加权QoS 明显大于不含关联分析的加权QoS。本文关联分析的平均加权QoS 为0.505，大于文献[15]的平均加权QoS（为0.496），表明本文所提服务关联QoS 感知模型有更好的性能。

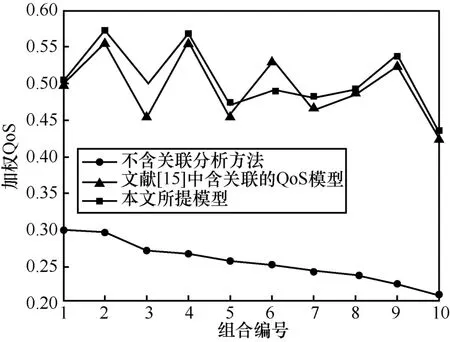
图6 加权QoS 对比分析

表5 服务组合加权QoS 的排名变化

在此基础上，分别以加权QoS 对服务组合进行排名。从表5 可以看出，采用不同的关联分析模型对不含关联分析的服务组合排名的变化不同。

例如，编号3 的服务组合不含关联分析时QoS1为[29.62,109.95,0.84,0.29,0.23]；利用文献[15]方法时QoS2为[26.38,106.5,0.83,0.37,0.39]，排名为8，下降5 名；采用本文方法时QoS3为[25.76,106.8,0.88,0.41,0.45]，排名为5，下降2 名。从整体上看，相较于QoS1而言，QoS2中属性平均增幅为总体平均增幅的0.77；QoS3中属性平均增幅为总体平均增幅的0.91。通过查证服务关联模型可以发现，业务实体关联中存在2 个合作时间分别为3 年和4 年的合作关系；统计关联中存在8 种常出现的组合，其对应关联规则的KULC 和IR 分别为0.79 和0.23，即较平衡的正相关，并且近2 个月各组合QoS 属性均有轻微的上升趋势。文献[15]中并未考虑服务组合关联规则强度和历史表现的影响，从而对编号3的QoS 属性优化程度相较于本文方法偏低，使排名下降更多，容易丢失存在关联较强的服务组合。

编号6 的服务组合不含关联分析时QoS1为[27.13,119.08,0.82,0.21,0.31]；利用文献[15]方法时QoS2为[24.1,115.23,0.86,0.38,0.45]，排名上升3 名；采用本文方法时QoS3为[23.38,115.55,0.87,0.38,0.48]，排名不变。从整体上看，相较于QoS1而言，QoS2中属性平均增幅为总体平均增幅的1.17，从而排名上升；QoS3中属性平均增幅为总体平均增幅的0.97，排名不变。根据描述模型中的关联关系发现，编号6 的服务组合的业务实体关联中存在3 个合作时间分别为1 年、2 年、5 年的合作关系；统计关联中存在8 种常出现的组合，其中组合(c1_s1,c14_s1)、(c1_s1,c9_s1)和(c10_s1,c14_s1)的描述模型中KULC＜0.5 和IR＞0.7 呈负向、不平衡关联，即关联组合强度弱，在加权QoS3总体呈上升的情况下，使该组合排名靠后，从而避免选择含较差关联规则的服务组合。

由此可见，接口关联、业务实体关联和统计关联在服务组合中QoS 的直接作用对单个服务选择和服务组合的选取都有较大影响。通过对比，体现了本文所提支持服务关联的QoS 感知评估模型的可行性和有效性。

5.3 业务实体关联中关联比与合作时间的影响（实验2）

为检验业务实体关联中关联比对制造云服务组合加权QoS 的影响，在当前时间为2020 年8 月1 日的条件下，分别对关联比例为20%、40%、60%、80%进行600 次迭代，发现得到Pareto 解的平均个数呈现如图7 所示的趋势。

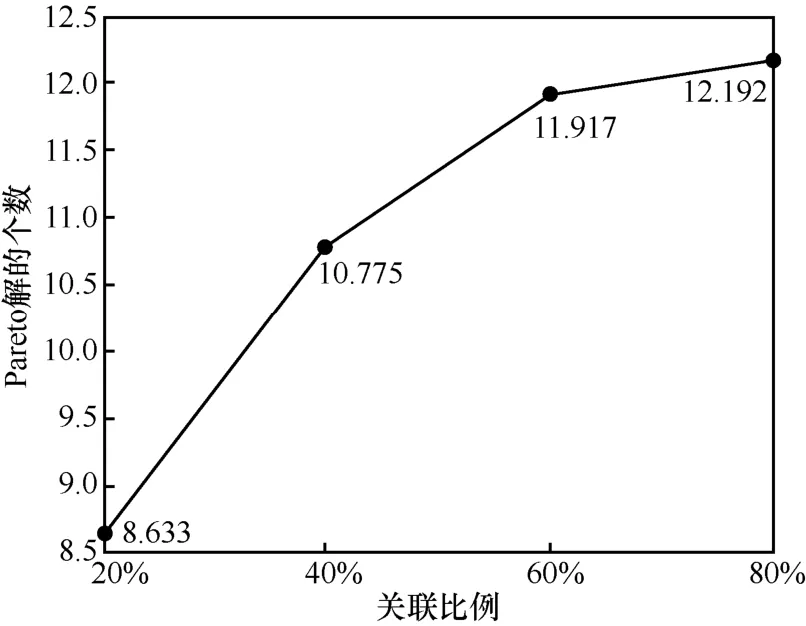
图7 不同关联比例下的Pareto 解的个数

从图7 中可以看出，随业务实体关联比例的变大，Pareto 解的平均个数逐渐增加。主要原因在于，关联比例的上升使满足约束条件的服务组合个数增多，即可行解的数量变多，从而使实验所得到Pareto 解的个数增加。

针对业务实体关联模型中合作时间对服务组合选择的影响，在实验1 的基础上进一步探讨。如图8 所示，由于合作时间形成的时间因子作用，含合作时间的加权QoS 相较于不含合作时间的加权QoS 都有不同幅度的增长。以服务组合各QoS 属性的均值来看，从不含合作时间的[24.23,114.27,0.86,0.41,0.42]优化为含合作时间的[23.72,113.26,0.87,0.44,0.46]，各个属性值都得到提升。

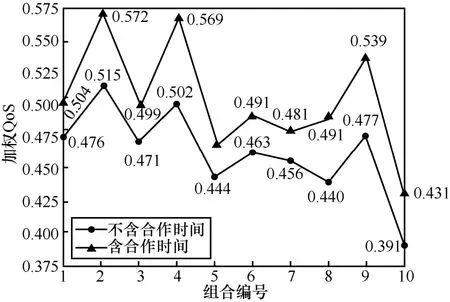
图8 不含合作时间与含合作时间的加权QoS

将2 种方案的加权QoS 进行排名，如表6 所示。从表6 中可以看出，编号5、7、8 的服务组合在业务实体关联模型中在不含合作时间和含合作时间的2 种情况下排名增幅发生了变化。

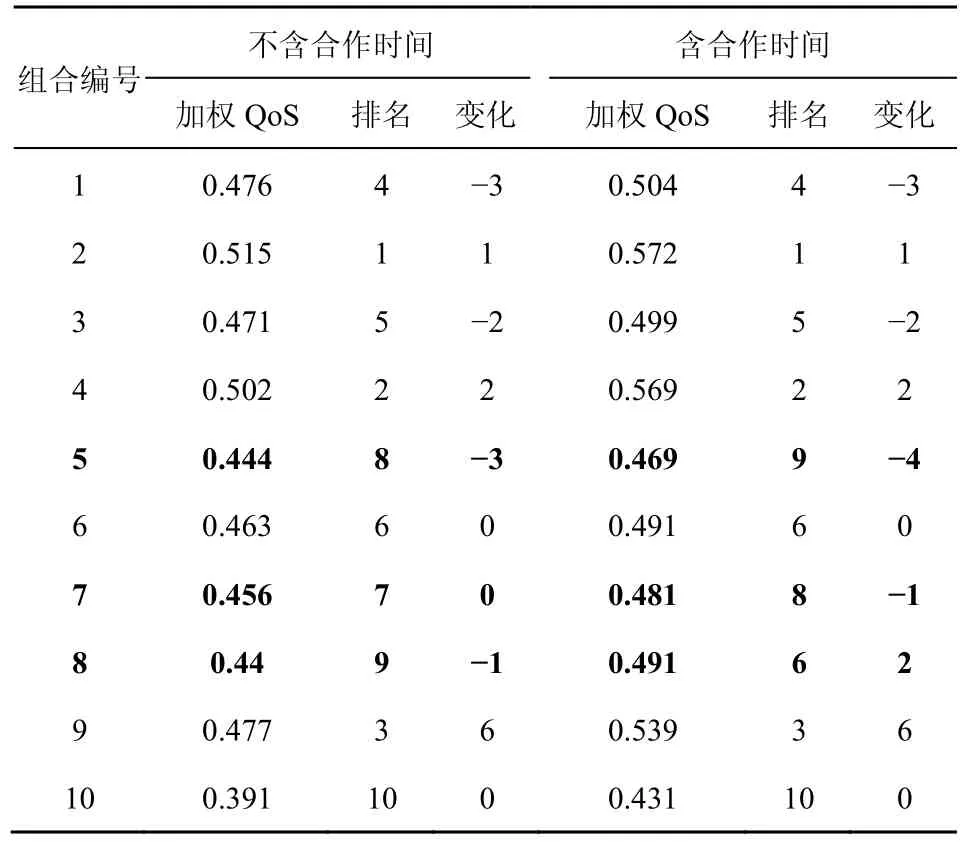
表6 不含合作时间与含合作时间的排名变化

根据各个服务的业务实体关联描述模型发现编号为8的组合方案包含2个4年的合作关系(c6_s1,c14_s3)、(c6_s1,c10_s1)和一个6 年的合作关系(c9_s2,c14_s3)。在不考虑合作时间时编号为8 的服务组合排名为第9 名，当引入合作时间后上升到第6名。由于合作时间较长，因此该方案服务提供商之间合作效率和成本具有更大优势。可见，含合作时间的业务实体关联模型能够有效地为服务需求方识别出合作时间相对较长、合作效果更好的服务组合，表明了在业务实体关联模型中引入合作时间的可行性。

5.4 统计关联中不同时间的影响（实验3）

为验证本文在统计关联中利用服务组合历史记录信息动态调整QoS 变化量的有效性，将在不同时间（2020 年6 月1 日、2020 年7 月1 日和2020 年8 月1 日）进行服务组合寻优，并对所有时间得到Pareto 解集合并去重，再次进行非支配排序，可以防止Pareto 解集的随机性，使某一时间未能找到某个Pareto 解所导致的结果不一致现象。表7 为各个时间得到的Pareto 解集。

如表7 所示，不同时间段得到加权QoS 排名前10 的服务组合解集相似，但由于个别服务组合加权QoS 不同，使排名有一定的变化。例如，服务组合(c1_s2,c4_s3,c9_s1,c11_s2,c13_s2)在6 月1 日时加权QoS 为0.542，排名第4，查证历史组合记录发现，6 月期间组合(c1_s2,c4_s3)和(c1_s2,c9_s1)绑定执行时QoS 呈下降趋势。(c1_s2,c4_s3)中c1_s2 的QoS 从[1.5,0.85,0.88,0.91]至[1.59,0.84,0.88,0.88]，c4_s3 的QoS 从[8.36,0.95,0.84,0.63]至[8.37,0.93,0.76,0.63]；(c1_s2,c9_s1)中c1_s2 的QoS 从[1.71,0.85,0.85,0.93]至[1.74,0.85,0.82,0.92]，c9_s1 的QoS 从[4.95,0.87,0.73,0.93]至[5.06,0.76,0.6,0.90]。其中第一个值为时间，越小越好，其余值为信誉度、可用性和可靠性，越大越好。由此可以看出，在6 月这2 种组合的执行效果欠佳，并且组合(c1_s2,c13_s2)和(c10_s1,c13_s2)的KULC 分别从0.87、0.89 下降至0.85、0.84，即组合关联性减弱，总体效果变差，从而使(c1_s2,c4_s3,c9_s1,c11_s2,c13_s2)组合方案在7 月1 日时加权QoS 变小为0.538，排名下降到第5 名。

此外，7 月期间组合(c4_s3,c9_s2)、(c9_s2,c12_s1)和(c12_s1,c14_s3)绑定频次增多且执行效果较好：(c4_s3,c9_s2)绑定执行次数增加3 次，且服务QoS 中时间的均值相较于6 月分别从8.84、6.87减少至8.25、6.01；(c9_s2,c12_s1)绑定执行次数增加2 次，且服务对应QoS 中时间的均值相较于6 月分别从6.75、5.92 下降至6.70、5.83；(c12_s1,c14_s3)绑定执行次数增加1 次，且该服务QoS 在4 个属性上都有提升。c12_s1 从[5.98,0.72,0.48,0.73]优化至[5.52,0.74,0.49,0.81]；c14_s3 从[4.05,0.8,0.95,0.69]优化至[3.51,0.75,0.96,0.74]。从而在8 月1 日时出现了新的优质服务组合(c1_s1,c4_s3,c9_s2,c12_s1,c14_s3)。

由此可见，利用本文所提统计关联模型可以有效地识别出近期执行较好的服务组合，通过动态调整QoS 变化量，使最终得到的服务组合方案时效性更强，更符合实际。

6 结束语

制造业生产过程复杂多变，服务质量会随时间和应用的不同动态发生变化，因此服务需求方往往需要更加切实有效的服务组合方案。因此，本文研究了制造云平台中服务组合的3 种关联关系，提出了支持服务关联的QoS 感知评估模型。下一步工作将对多目标优化算法进行对比选择并做出相应的改进，提升算法性能，以适应制造云服务组合问题，得到更优质的解集。此外，进一步探索制造云服务关联的自适应调整，提升服务质量真实性。

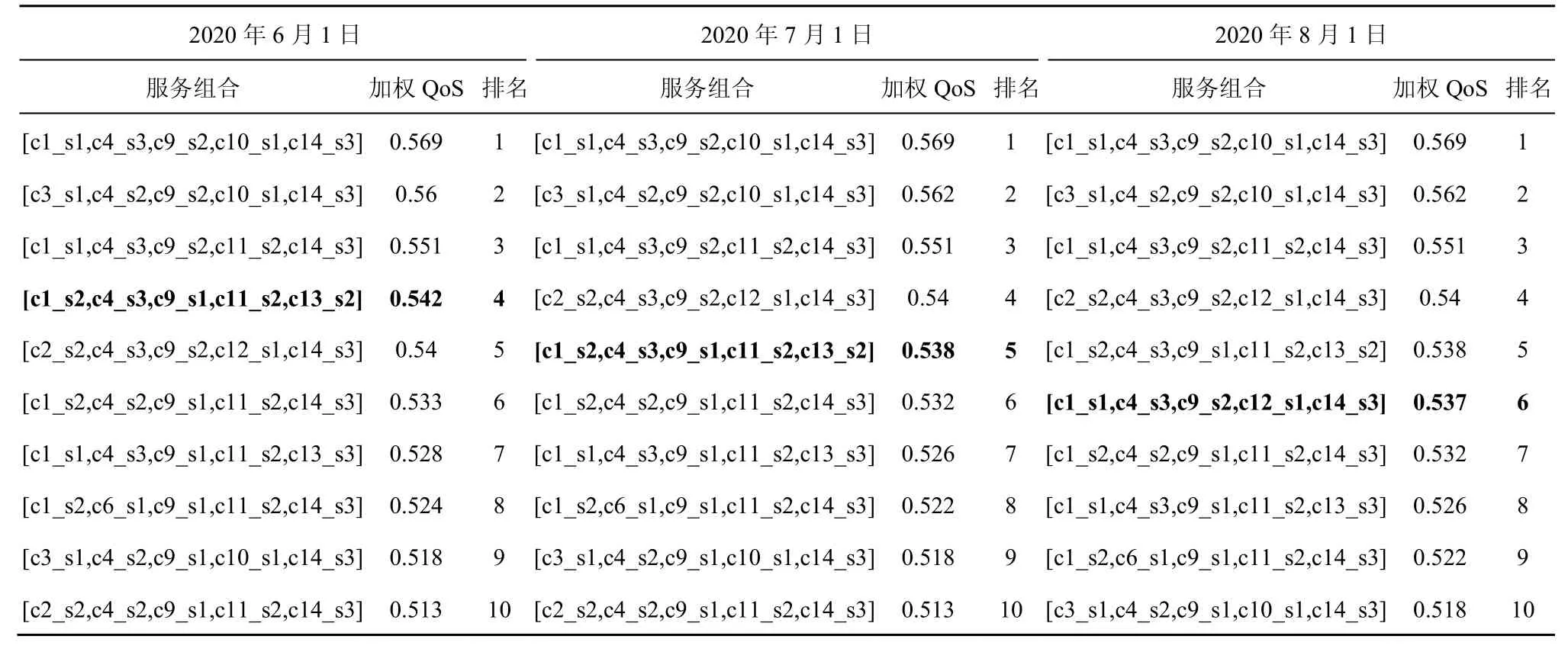
表7 不同时间加权QoS 排名前10 的Pareto 解集