格上基于身份的增量签名方案

田苗苗，陈静，仲红

（安徽大学计算机科学与技术学院，安徽 合肥 230601）

1 引言

随着信息化的深入发展，数字信息在当今社会发挥着越来越重要的作用，保障数字信息的完整性和不可伪造性是现代社会健康发展的前提。数字签名[1]是一种基础的密码学原语，可以用来保证数字消息的完整性、发送者身份的不可抵赖性等，广泛应用于网上银行、电子政务、电子合同等诸多领域。传统的数字签名没有考虑消息之间的联系，每次签署消息所需的开销与消息的长度成正比，难以满足一些特定应用场景的需求。例如，在面向自然灾害预防或天气预报的环境传感网络中，分布于不同地理位置的一系列传感器需要监测环境数据并将其上传到上层收集设备保存[2]，为了保证这些监测数据的真实性，需要对其进行签名。由于要精准地进行自然灾害或天气预测，这些传感器需要持续监测并实时更新监测数据，而通常连续的监测数据，如温度和湿度数据等仅有微小的差异。随着监测任务的持续进行，数据不断增加，如果采用传统的数字签名方法，每次更新数据都必须重新计算签名，会导致传感器的开销很大。为了降低传感器的开销，延长传感器的使用寿命，可以采用增量签名[3]方案对这些监测数据进行签名。

增量签名的概念由Bellare 等[3]于1994 年提出，其基本出发点是，数字签名主要包括对消息进行哈希运算和对哈希结果进行签名两部分，如果哈希函数具有增量性，那么当已知一个消息的哈希值时，用户可以快速得到另一个相似消息的哈希值，对该哈希值进行签名，即可得到新消息的签名。由于增量签名方案可以加快相似消息的签名过程，使签名生成时间与消息间的变化量成正比，因此对数据连续更新的场景或者存在大量相似数据的场景，采用增量签名方案而非传统签名方案，可以大大降低系统的整体开销。区块链是当前的一个研究热点，将一个交易加入区块链中的前提是确保该交易的完整性和不可伪造性，为此需对该交易签名并向全网广播，由其他用户检查签名的有效性，仅当签名有效时才将该交易加入区块链[4]。由于区块链中通常存在较多的相似数据，因此采用增量签名方案对交易进行签名有望大幅提高区块链系统的效率。最近，著名区块链公司Kadena 已经在其企业级区块链上采用了增量签名算法。

增量签名这一概念被提出以来，许多增量签名方案[3,5-6]相继被提出，然而现有的增量签名方案都依赖于公钥基础设施（PKI,public key infrastructure），用户的公钥是一串随机字符，需要通过数字证书绑定用户的身份与其公钥的匹配关系，这会给系统带来额外的存储开销和计算开销。为了解决这个问题，本文借鉴基于身份的密码学思想[7]，提出了基于身份的增量签名概念，用户使用能唯一标识其身份的字符串（如电话号码、邮箱地址等）作为其公钥，相应的私钥由可信的私钥生成器（PKG,private key generator）根据系统主密钥和用户身份生成，从而消除了传统增量签名方案存在的证书管理问题。

此外，本文利用格上相关困难问题——标准的小整数解（SIS,small integer solution）问题[8-9]，设计了一种具体的基于身份的增量签名方案，该方案在标准模型下对适应性选择身份和选择消息攻击满足不可伪造性。基于格的密码学也是当前的一个研究热点，与基于离散对数和大数分解等传统困难问题的密码方案相比，基于格的密码方案有望抵抗量子计算机的攻击[10]，并且仅需要向量点乘、线性求和以及模运算等简单操作，计算效率较高。近年来，基于格的数字签名方案受到人们的广泛关注，格上基于身份的各类签名方案也被相继提出，如格上基于身份的（标准）签名方案[11-16]和环签名方案[17-18]等。然而，这些方案要么仅能在随机预言模型下证明是适应性安全的[13-14,16-17]，要么只能达到标准模型下的选择安全性（即仅能实现选择身份攻击下的不可伪造性）[11-12,18]。由于随机预言模型下证明安全的方案在实际应用中不一定安全[19]，因此构造标准模型下适应性安全的格上基于身份的签名方案具有重要的理论和现实意义。如果不考虑增量性，本文方案也可以看作一种在标准模型下对适应性选择身份和选择消息攻击满足不可伪造性的格上基于身份的签名方案。

具体地，本文的主要贡献包括以下3 个方面。

1) 本文提出了基于身份的增量签名概念及模型，消除了以往增量签名中存在的证书管理问题，提高了增量签名方案的实际效率。

3) 本文证明了在标准的小整数解困难假设下，所提格上基于身份的增量签名方案在标准模型下满足适应性选择身份和选择消息攻击下的不可伪造性。

2 预备知识

2.1 符号定义

本文的安全参数为n。令ℝ 和ℤ 分别表示实数集和整数集。给定正整数d，令[d]表示集合{0,…,d−1}，令BitDecompb(d)表示d的维比特分解，其中b为正整数。令矩阵A的格拉姆−施密特正交化为，并且令其最大奇异值为s1(A)=maxu‖Au‖，其中，u是任意的单位向量，‖ ⋅‖是 ℓ2范数。

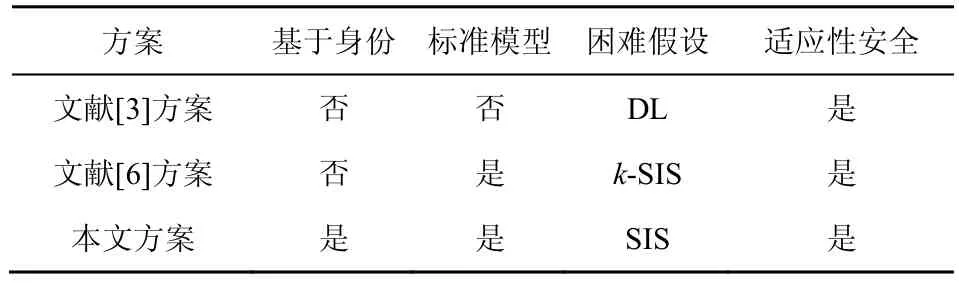
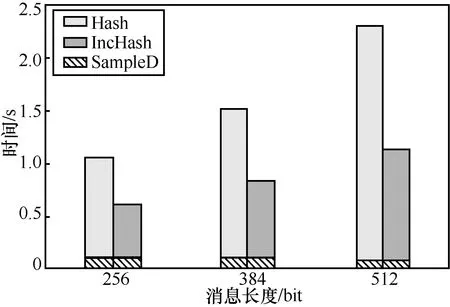
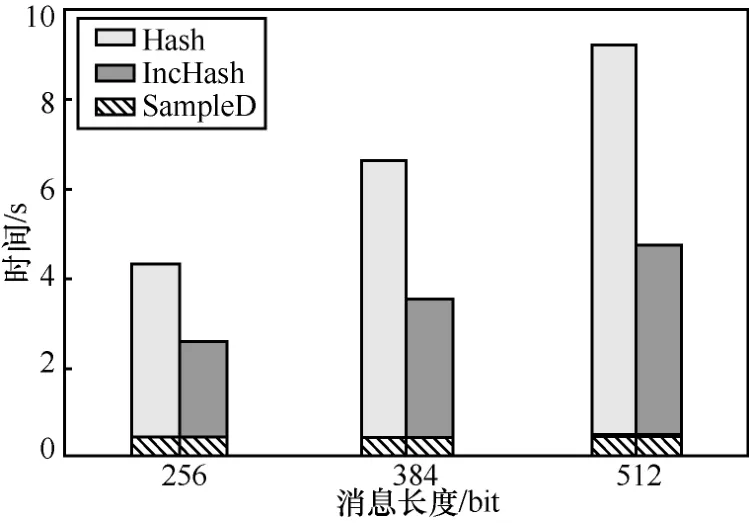
如果对任意的常数c，存在整数N，当n>N时，f(n)

2.2 基于身份的增量签名方案

本节介绍基于身份的增量签名方案的定义及安全模型。

定义1基于身份的增量签名方案由以下5 个概率多项式时间算法组成，分别为系统建立算法Setup、私钥提取算法Extract、标准签名算法Sign、增量签名算法IncSig 以及签名验证算法Verify。各算法的具体描述如下。

Setup。输入安全参数n，输出系统主公钥mpk和主私钥msk。

Extract。输入系统主公钥mpk 和主私钥msk，以及身份id，输出该身份所对应的私钥skid。

Sign。输入系统主公钥mpk、身份id 及其对应的私钥skid，以及消息μ，输出消息μ的签名sig。

IncSig。输入系统主公钥mpk、身份id 及其对应的私钥skid、一个有效的消息签名对(μ,sig)，以及新消息μ′，输出消息μ′的签名sig′。

Verify。输入系统主公钥mpk、身份id 和一个消息签名对(μ,sig)，如果sig 是身份为id 的用户对消息μ的有效签名，则输出1；否则输出0。

基于身份的增量签名方案首先要满足正确性，即对任意的身份id 和消息μ，如果算法Setup(n)、Extract(mpk,msk,id)以及Sign(mpk,id,skid,μ)均正确执行，则：1) Verify(mpk,id,μ,sig)应以极大概率输出1；2) 对任意一个消息μ′以及一个有效的消息签 名 对(μ,sig)，满 足 Verify(mpk,id,μ,sig)=1，Verify(mpk,id,μ′,IncSig (mpk,id,skid,μ,sig,μ′))应以极大概率输出1。

根据传统增量签名的适应性选择消息安全模型[3]、基于身份签名的适应性选择身份和选择消息安全模型[14,23]，可定义基于身份的增量签名方案在适应性选择身份和选择消息攻击下的安全性。

定义2如果对任意的多项式时间敌手A，其赢得以下游戏的概率是可忽略的，则称该基于身份的增量签名方案满足适应性选择身份和选择消息攻击下的不可伪造性。游戏由敌手A 和挑战者C 执行，包括以下5 个阶段：系统建立阶段、私钥提取询问阶段、标准签名询问阶段、增量签名询问阶段和伪造阶段。

系统建立阶段。挑战者C 运行算法Setup(n)生成系统主公钥mpk 和主私钥msk，然后将主公钥mpk 发送给敌手A，并初始化参数α=0。

私钥提取询问阶段。敌手A 可以适应性地向挑战者C 询问身份id 所对应的私钥，挑战者C 运行算法Extract(mpk,msk,id)生成私钥skid，并将其发送给敌手A。

标准签名询问阶段。敌手A 可以适应性地向挑战者C 进行标准签名询问。当敌手A 询问身份为id的用户对消息μ的标准签名时，挑战者C 运行算法Sign(mpk,id,skid,μ)生成相应的签名sig，并将其发送给敌手A 。然后挑战者C保存(μα,sigα)=(μ,sig)，并令α=α+1。

增量签名询问阶段。敌手A 也可以适应性地向挑战者C 进行增量签名询问。不失一般性地，假设2 个相似消息之间只相差1 bit。当敌手A 询问身份为id 的用户对消息μ′的增量签名时，它需要发送id 以及一个三元组(i,j,v)，其中，i∈[α]，表明μ′是μi的第j位被v代替所得的新消息。挑战者C 首先找到有效的消息签名对(μi,sigi)，然后运行算法IncSig (mpk,id,skid,μi,sigi,μ′)生成相应的签名sig′，并将其发送给敌手A，最后挑战者C 保存(μα,sigα)=(μ′,sig′)，并令α=α+1。

伪造阶段。敌手A 伪造一个关于身份id*的伪造消息签名对(μ*,sig*)，若满足以下条件，则敌手A 赢得游戏。

1) 敌手A 没有对身份id*进行过私钥提取询问，也没有对μ*进行过标准签名询问或关于μ*的增量签名询问，即μ*∉{μ0,μ1, …,μα−1}。

2) 算法Verify(mpk,id*,μ*,sig*)=1。

2.3 格基础知识

2.4 离散高斯分布

2.5 格陷门函数

基于格的陷门函数是格密码学的重要工具之一，传统的格陷门是格的一个短基。本文提出的格上基于身份的增量签名方案采用文献[21]的G−陷门概念及其相关算法，分别为陷门生成算法TrapGen、原像采样算法SampleD 和陷门委派算法DelTrap。这种陷门函数的参数较小，计算和存储开销也较少。

2.6 可编程哈希函数

可编程哈希函数（PHF,programmablehash function）的概念最初由Hofheinz 等[26]提出，可以用来构造标准模型下安全的密码方案。简单来说，可编程哈希函数有2 种工作模式，即正常模式和陷门模式。正常模式包含H.Gen和H.Eval这2 种算法，而陷门模式包含H.TrapGen 和H.TrapEval这2 种算法。在拥有陷门信息的情况下，这2 种模式是不可区分的，因此可以在安全性证明中使用陷门模式模拟正常模式。本文采用Zhang 等[20]提出的基于格的高效可编程哈希函数来嵌入身份信息。下面给出无覆盖集合族的概念。

上述引理表明，该可编程哈希函数存在较好的模拟方法，可以在安全性证明中模拟该函数。

3 具体方案

3.1 方案描述

本文方案各算法的具体实现过程如下。

1) 系统建立算法

3.2 参数设置

4 方案分析

4.1 正确性分析

定理1本文提出的格上基于身份的增量签名方案满足正确性。

证明考虑标准签名和增量签名2 种情况。

综上，本文提出的增量签名方案是正确的。证毕。

4.2 安全性分析

定理2如果小整数解问题是困难的，则本文提出的格上基于身份的增量签名方案对适应性选择身份和选择消息攻击是不可伪造的。

4.3 对比分析

本节将本文方案与基于PKI 的增量签名方案和基于身份的签名方案分别进行比较。

1) 与基于PKI 的增量签名方案对比

表1 给出了本文方案与几种增量签名方案的特征比较。文献[3]和文献[6]的方案都是基于PKI 的，存在证书管理问题。文献[3]的方案基于离散对数（DL,discrete logarithm）问题的困难性，在随机预言模型下对适应性选择消息攻击是安全的。文献[6]的方案基于格上k次小整数解（k-SIS,k-small integer solutions）问题的困难性[27]，在标准模型下对适应性选择消息攻击是安全的。然而由于将k-SIS 问题规约到标准SIS 问题会增加乘法因子k！，其中k与签名次数有关，因此文献[6]中方案的签名次数较有限。与这2 种方案相比，本文方案不仅消除了证书管理问题，而且在标准模型下基于标准的SIS 问题证明了方案满足适应性选择身份和选择消息攻击下的不可伪造性。

表1 3 种增量签名方案对比

2) 与格上基于身份的签名方案对比

表2 给出了本文方案与几种格上基于身份的签名方案的比较结果，其中n表示安全参数，。从表2 可以看出，虽然本文方案相比文献[11-15]中的方案而言，在公开参数大小、签名密钥大小和签名长度等方面优势不明显，但本文方案的安全性较高。具体地，文献[13-14]中的方案仅在随机预言模型下达到适应性选择身份和选择消息攻击下的不可伪造性，文献[15]中的方案在随机预言机模型下仅对选择身份攻击是安全的，而文献[11-12]中的方案虽然是在标准模型下可证明安全的，但这些方案只对选择身份攻击是安全的。

此外，本文方案还具有增量性。假设2 个消息仅相差1 bit，则当已知一个消息的哈希值时，采用本文方案计算新消息的哈希值仅需一次矩阵加法运算即可，而完整的哈希计算则需要计算 ℓ+1次矩阵加法。由于ℓ 通常较大，因此本文方案可以加快标准签名算法的签名过程。

4.4 性能评估

本节将通过具体实验来展示增量签名算法相对于标准签名算法的性能提升情况。

根据3.1 节的方案描述可知，标准签名算法与增量签名算法都需要运行SampleD 和计算消息的哈希值（由于矩阵Aid具有一定的稳定性，因此这里忽略其计算开销），然而标准签名算法的消息编码方式为，其计算时间与整个消息μ的长度成正比，增量签名算法的消息编码方式为，其计算时间仅与消息的改变量（μ′和μ之间的比特差异数）成正比。因此，当需要对d个连续变化的数据进行签名时，用增量签名方案仅需执行一次标准签名算法和d−1 次增量签名算法，而采用标准签名方案需执行d次标准签名算法。直观上看，增量签名算法的运行时间要比标准签名算法的少，因此增量签名方案非常适用于处理数据仅有细微差别的大数据系统。

表2 本文方案与几种格上基于身份的签名方案对比

下面给出各算法的实验运行结果，具体包括标准签名算法、增量签名算法以及签名验证算法的计算开销。

本文方案的实验代码采用 C++11 编写、g++5.4.0 编译。实验由配置了Ubuntu 16.04 LTS 系统、Intel Core i5-7500 CPU 和16 GB 内存的PC 运行。本文实验选取2 组数据，分别是n=128 和n=256。消息长度分别为256 bit、384 bit 和512 bit，增量签名的消息改变量为原消息长度的一半。在本文实验中，令，其中ε=2−80，其他相关参数如表3 所示。所有实验结果均为运行10 次实验的平均值。

表3 实验参数的具体设置

图1 和图2 分别展示了当n=128 和n=256 时，标准签名算法和增量签名算法的计算时间比较。标准签名算法的计算时间包括计算消息哈希值以及执行SampleD 的时间，而增量签名算法的计算时间包括计算消息增量哈希值以及执行SampleD 的时间，其中Hash 表示计算消息哈希值的时间，IncHash表示计算消息增量哈希值的时间，SampleD 表示执行SampleD 的时间。从图1 和图2 可以看出，随着消息长度的不断增加，Hash 和IncHash 都会增长，但IncHash 的值更小。具体地，当n=128 时，增量签名算法的整体计算效率相比标准签名算法提高了41.9%～50.2%；当n=256 时，增量签名算法的整体计算效率相比标准签名算法提高了39.9%～48.3%。

表4 为不同参数下签名验证算法Verify 的计算时间对比。由于该算法的执行时间对标准签名算法和增量签名算法都是相同的，因此表4 列出了在不同的n和消息长度的情况下，Verify 算法的执行时间变化情况。从表4 中可以看出，随着n和消息长度的增加，Verify 算法所需的时间也会增加，但其绝对值仍较小。

图1 当n=128 时，2 种签名算法的计算时间对比

图2 当n=256 时，2 种签名算法的计算时间对比

表4 不同参数下验证算法的计算时间对比

5 结束语

本文提出了基于身份的增量签名概念，并基于格上困难问题设计了一种具体方案。在标准的小整数解困难假设下，本文方案在标准模型下对适应性选择身份和选择消息攻击是不可伪造的。与基于PKI 的增量签名方案相比，本文方案消除了公钥证书的管理问题，提高了方案的实际使用效率。此外，与格上基于身份的签名方案相比，本文方案不仅具有增量性和更好的计算效率，而且安全性也较高。