拉臂机构力学特性分析及结构优化

唐山学院交通与车辆工程系 唐山 066300

0 引言

随着中国社会经济发展速度的不断加快，居民对生活环境质量的要求不断提高，致使环卫部门需要处理垃圾的样式和数量不断增多，拉臂式垃圾车作为一种车厢可卸式垃圾车，装卸效率高，作业时间短，可改善环卫工人工作条件，广泛应用于环保作业中[1,2]。目前，国内对拉臂机构的应用研究分析主要用动载系数来表示拉臂机构作业时所受的动载荷，以静强度作为拉臂机构的设计准则[3,4]。由于拉臂机构实际受到的载荷多为动态载荷，动载系数以及静强度都无法准确地描述实时受力状态，传统的拉臂机构设计方法很难考虑其复杂的受力及变形情况，而有限元的结构模态分析法可以很好地解决此问题。为此，本文以某公司研制的拉臂式垃圾车总成为例，利用有限元技术对结构进行分析并进行局部改进，进而提高拉臂机构的安全系数，为确保该产品正常使用提供依据。

1 拉臂机构的工作原理及组成

拉臂式垃圾车可以完成换箱和倾斜功能。当拉臂机构执行换箱动作时，垃圾箱安全钩被打开，举升液压缸伸出，垃圾箱被推到地面。当垃圾箱提起到副车架上时，钩子先钩住垃圾箱的环，然后举升液压缸缩回，以主轴旋转的逆时针方向旋转拉臂，将垃圾箱提起副车架上；当垃圾车倾卸工况时，垃圾箱安全钩保障拉臂和垃圾箱不分离的状态，将副车架后部导向轮顺时针旋转一定角度，以抬起垃圾箱，直到清除垃圾为止。当滑架返回其原始位置时，液压缸缩回，拉臂机构仍将以导轮为旋转轴，并逆时针旋转直到垃圾箱复位。

拉臂式垃圾车的拉臂机构的结构布置如图1所示，拉臂的一端与拉臂缸的活塞杆端相连，铰接在铰链支点B上。拉臂缸的缸头端连接至副车架的前部，并铰接至铰链支撑点A。连杆架的后轴连接至副车架的后部，并铰接至铰链支撑点D，以形成联动架枢轴。

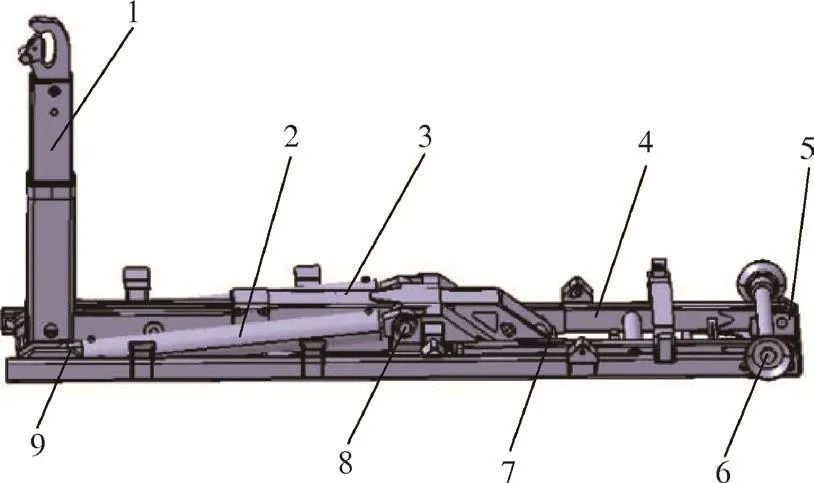
图1 拉臂机构的结构布置

2 拉臂机构力学特性分析

根据拉臂结构的受力情况，危险工况分别为装箱过程、物料倾卸过程与卸箱过程。物料倾斜过程的旋转轴与装卸过程不同，拉臂液压缸活塞杆回转半径DB大于装卸箱的回转半径OB，则物料倾斜过程所需的液压缸推力和拉力小于装卸过程液压缸推力和拉力，故文中仅对装箱工况和卸箱工况进行拉臂架装置的受力分析与计算。

在装箱与卸箱过程中，拉臂机构主要受三个力影响，即：举升液压缸对固定座的拉力或推力，副车架对固定座主旋转轴的支撑力，垃圾箱对钩臂的拉力。拉臂机构在装卸工况其拉臂钩手处出现最大载荷时垃圾箱与导向轮接触，受力简图如图2所示。

图2 拉臂机构在装卸过程的受力简图

垃圾箱对拉臂钩手的拉力从垃圾箱钩环被拉臂上的钩手拉起时开始，直至垃圾箱被完全吊起，此时拉力出现骤增现象，在垃圾箱体与联动架上的滚轮接触之前，拉力会缓慢变小，故此时拉臂钩手处将出现最大载荷。对垃圾箱进行受力分析，由C＇点受力平衡与力矩平衡方程可得

联立可得地面对垃圾箱的支撑力

由边角关系可得

已知满载时垃圾箱质量为7.84 kN，h＝0.9 m，L4＝2.3 m，H＝1.4 m，L＝3.1 m，α＝31°，可得拉臂钩手处的拉力为

卸载过程与装箱过程恰好相反，可以将其视为装箱过程的逆过程，通过受力简图分析，拉臂和翻转架从水平位置转过90°时，拉臂折弯处应最容易受损，此时垃圾箱体前轮处于离开地面，后轮接触地面状态，且垃圾箱未与副车架上的导向轮接触，亦可求得垃圾箱对拉臂钩手拉力的分力

3 拉臂机构静态有限元分析

3.1 拉臂机构有限元模型的建立

拉臂机构材料为Q550D，泊松比为0.3，弹性模量为2.0×1011Pa，材料密度为7 850 kg/m3，屈服强度为550 MPa，抗拉强度670 MPa，该模型共包含292 050个节点；115 491个单元，如图3所示。

图3 拉臂机构有限元计算模型

3.2 装箱工况静力学分析

在拉臂钩手内侧施加拉力，根据分析计算可知，当拉臂转角43.5°时，拉臂钩手受到的极大值为49.087 kN。将边界条件带入仿真模型，机构应力分布与变形量如图4、图5所示。装箱过程中，最大变形发生在拉臂勾手上，最大值为14.12 mm。应力集中在伸缩套筒与拉臂连接的折弯处，应力值为349 MPa，此处是连接部位，形变严重，弯矩较大，装箱工况下拉臂机构各处应力均小于屈服极限，且安全系数为1.57＞1.5，满足其强度要求。

图4 装箱过程拉臂机构的应力分布

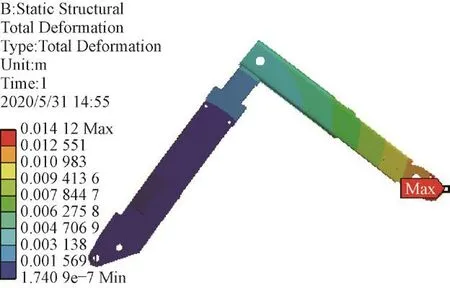
图5 装箱过程拉臂机构的变形量情况

3.3 卸箱工况静力学分析

拉臂的钩臂内侧施加载荷，Fx＝-56.474 kN，Fy＝10.963 kN，应力与变形量如图6、图7所示。拉臂机构在卸箱过程中，拉臂钩手变形量最大，为13.6 mm。应力集中在伸缩套筒连接到拉臂弯曲处，最大值为470 MPa，连接部的变形更严重，施加在拉臂钩上的拉力主要是沿X轴负方向的。经计算可知，卸箱工况下各部位的应力值小于屈服极限，但其安全系数为1.17＜1.5，不满足强度要求。

图6 卸箱过程拉臂机构整体的应力分布

图7 卸箱过程拉臂机构的变形量情况

4 拉臂机构的模态分析

4.1 拉臂机构动态性能要求

结合拉臂式垃圾车实际工况下的外界激励，确定其计算频段，避免拉臂式垃圾车产生共振现象。主要的外部激励是：

1）拉臂式垃圾车在普通公路上行驶时，会受到路面的刺激。由于垃圾车主要在平坦的道路上行驶，其激励频率一般为1～3 Hz，故该频率更容易避免。

2）拉臂式垃圾车正常行驶速度为50 km/h，因传动轴引发的激励频率为38 Hz左右，此频率也很容易避免。

3）该拉臂式垃圾车选用的发动机型号为TC4EG 170-50，其最低空载转速（怠速）为（600±50） r/min，最大扭矩转速为1 300～1 800 r/min，发动机的最低空载转速时的激励频率为18.3～21.7 Hz，最大扭矩转速时的激励频率为43.3～60 Hz，故发动机的常用工作频率为18.3～21.7 Hz和43.3～60 Hz。

4.2 模态分析结果

在Ansys有限元软件中得到了拉臂机构的最小12阶固有频率，如表1所示。

表1 各阶固有频率与振型

4.3 拉臂机构整体模态评价

1）分析得出的12阶固有频率和振型，拉臂机构的频率平稳增加，没有突变现象。

2）该拉臂机构的第一阶模态频率为26.75 Hz，第二阶模态频率为31.52 Hz，两者均避开了路面激振频率，也不在发动机最低空载转速频率和最大扭矩转速频率内。第三至第十二模态频率高于发动机的工作范围频率，故可以有效避免拉臂机构与发动机之间的共振现象。

3）拉臂机构的12阶模态频率均不在平缓路面引起的激励频率内，拉臂机构不会与路面激励产生共振。故可以确定拉臂机构不会与外界激励产生共振，拉臂机构具有良好的动态特性，符合拉臂机构设计要求。

5 拉臂机构的优化

5.1 拉臂机构的局部修改

经拉臂机构静力分析可知，在卸箱工况下强度不足。故需对拉臂机构进行局部修改，以达到符合静态性能的目的。对伸缩套筒与拉臂下部折弯的连接处采取一些必要的改进，减少伸缩套筒与拉臂下部折弯连接处的受力，在薄弱部位增加加强板以提高此位置的刚度，减少危险部位变形量，提高拉臂机构的强度。在伸缩套筒和拉臂下部弯曲的接缝处增加了2个三角形加强板，可以提高此处的弯曲强度，改进后的模型如图8所示。

图8 折弯处优化后的模型

在伸缩套筒的上下两端增加方形管，使伸缩套筒在拉臂机构工作时不易损坏，且此方案容易实施，不会对拉臂机构运行中的其他部件产生干涉，改进后的模型如图9所示。

图9 优化后的伸缩套筒模型

5.2 优化后的拉臂机构静力学分析

5.2.1 装箱工况分析

优化后模型的应力分布与变形量情况如图10、图11所示，其最大应力为268.37 MPa，,与未优化前的拉臂机构装箱过程相比，最大应力值减小了81.42 MPa，减小幅度为23.3%，且满足强度要求。最大变形量为12.643 mm，与未优化前的拉臂机构装箱过程相比，最大变形量减小了1.477 mm，减小幅度为10.46%。

5.2.2 卸箱工况分析

优化后的模型，其应力与变形量分布情况如图12、图13所示，优化后其最大应力为355.85 MPa，与未优化时拉臂机构卸箱过程相比，最大应力值减小了114.78 MPa，减小幅度为24.9%，优化后拉臂机构的安全系数为1.55，此时的拉臂机构符合强度要求；最大变形量为12.015 mm，与未优化前的拉臂机构卸箱过程相比，最大变形量减小了1.593 mm，减小幅度为11.7%。

图10 优化后拉臂机构在装箱过程的应力分布

图11 优化后拉臂机构在装箱过程的变形量分布

图12 优化拉臂机构卸箱过程中的应力分布

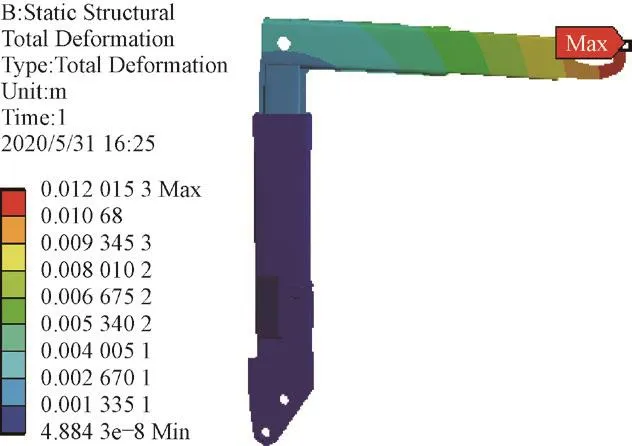
图13 优化后拉臂机构在装箱过程的变形量分布

6 结论与展望

文中在拉臂机构力学特性分析的基础上，进行了拉臂机构装箱过程和卸箱过程的静态、动态特性分析研究，为拉臂机构优化设计良好的理论基础，主要结论如下：

1）对拉臂机构进行力学特性分析，计算得出拉臂钩手在装、卸箱过程的最大载荷；建立了拉臂机构有限元模型，通过对拉臂机构装、卸过程的静态有限元分析，得出拉臂机构应力集中部位，以及在不同过程中的最大应力值，并对拉臂机构进行模态分析以探讨其动态性能。

2）有限元模态分析结果表明该拉臂机构前十二阶固有频率在要求的频率范围内，有效避免了共振现象的发生，故整个拉臂机构满足动态特性的条件，符合拉臂机构设计的要求，并为改进拉臂机构结构设计提供了理论依据。

3）结合前期对拉臂机构进行的静力学分析结果，对拉臂机构的伸缩套筒和伸缩套筒与拉臂下部折弯的连接处进行了改进，装、卸应力幅度分别减小23.3%与24.9%，最大变形量分别降低了10.46%与11.7%，提高了拉臂机构的工作强度与可靠性，为确保该产品正常使用提供依据。