基于指数分层结构算法的数据可信度评估模型设计

廖嘉炜，吴永欢，杜舒明，邹时容，徐炫东

(广州供电局有限公司，广东 广州 510620)

0 引 言

数据资产管理的数据对象存在规模大、来源多样、格式繁杂、采集实时等特征，尤其是数据的大量递增，以及格式的多样化，给数据资产管理带来了严峻的挑战。对数据资产进行管理能够为企业的发展管理、控制与科学决策提供有力的数据支撑[1-4]。但不是所有的数据都可以称之为数据资产，只有达到一定可信度的数据才能成为数据资产。由此可见，数据可信度是判断数据是否为数据资产的重要依据之一[5-7]。因此，对数据可信度进行评估是数据资产管理的重要组成部分。在此基础上，设计数据可信度评估模型，通过模型计算来量化评估数据可信度，能够有助于数据资产的管理。

目前，在数据可信度评估领域，已有一些相对成熟的方法，如文献[8]提出了基于D-S理论的多源数据可信度评估模型，文献[9]提出了基于聚类云模型的小样本数据可信度评估模型。然而，由于传统的评估模型过程较为复杂，导致分类适应性较差，且数据的查全性较差，难以适应目前数据资产管理中对无形数据的可信度评估，评估局限性较大。

指数分层结构算法是基于拓扑结构，对亚超度量空间和指数分层结构树进行优化后生成的一种算法，具有较好的分类能力和较强的适应性，且计算过程清晰，便于在数据可信度评估的过程中及时回溯查找[10-12]。

综上所述，为提高数据可信度评估质量及数据资产管理效果，本文引入指数分层结构算法，设计了一种新的数据可信度评估模型。首先建立数据可信度评估指标体系；然后补充待评估数据集中的缺漏数据，通过归一化处理数据形成数据集合，并根据数据间的相关系数建立亚超度量空间和指数分层结构树，完成数据处理；最后基于层次分析评估数据可信度评估模型。实验结果表明，上述评估过程具有更强的分类适应性和数据查全能力。

1 基于指数分层结构算法的数据可信度评估模型设计

1.1 建立数据可信度评估指标体系

在数据资产管理中，对数据的可信度进行准确评估时需建立可信度评估指标体系。本文选取的数据具有一般性，能够应用在常见的数据资产管理中。根据实际的数据资产类型，通常可总结出7个一级可信度评估指标以及12个二级可信度评估指标，可建立如表1所示的数据可信度评估指标体系。

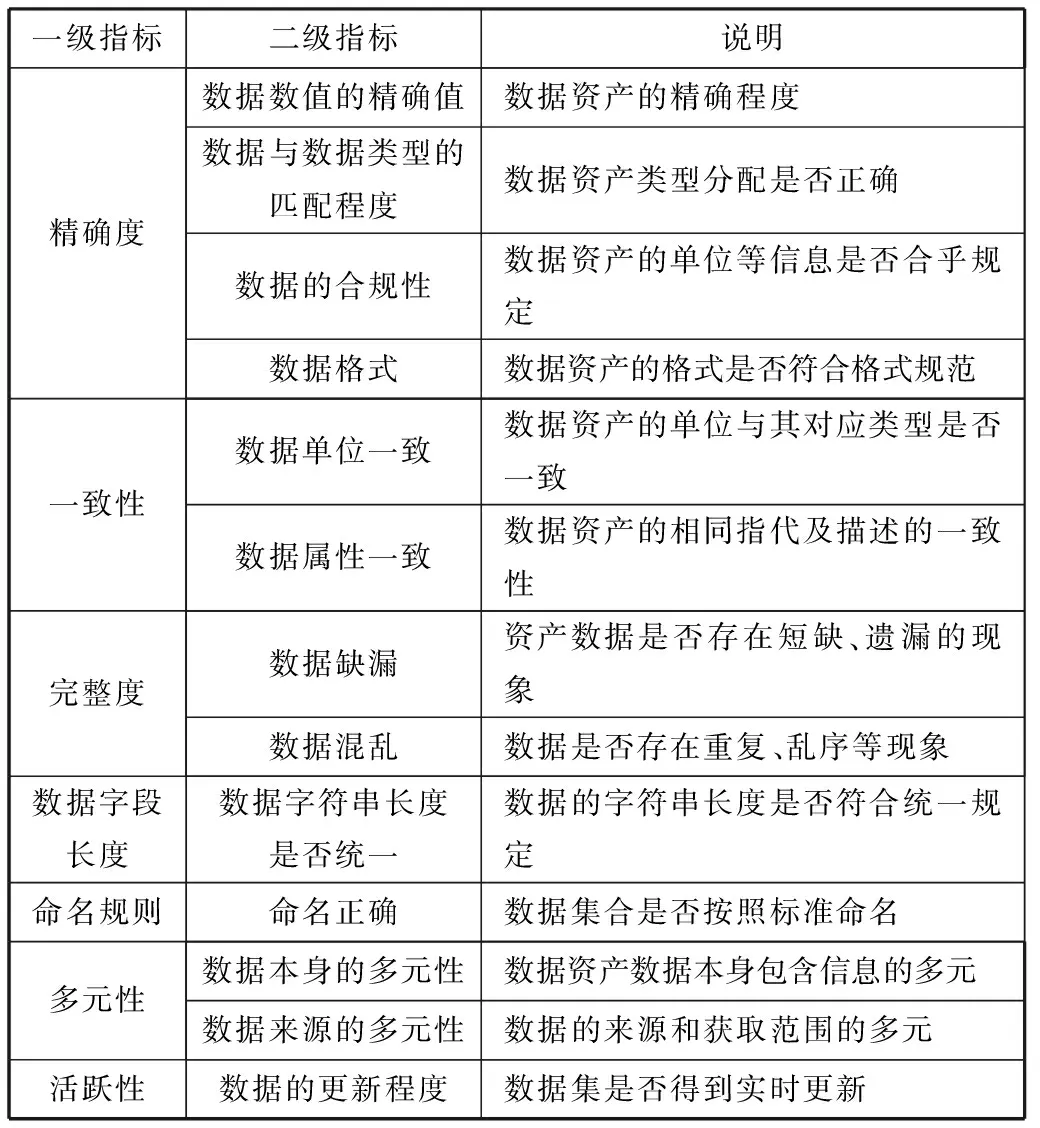
表1 数据可信度评估指标体系

在建立如表1所示的数据可信度评价指标体系后，为方便数据可信度评估模型的运行，需对数据进行预处理，再应用指数分层结构算法对数据可信度进行评估和判断。

1.2 待评估数据预处理

为避免因数据存在缺漏、重复等情况而对数据可信度评估过程造成影响，降低数据评估精度，需在评估前对数据进行一定的预处理。

对于待评估数据中存在缺漏的情况，采用如下方式进行数据缺漏填补：对于数据间存在的具有一定周期性关系的缺漏数据，可以利用相同时间段的同类型数据近似补充；若缺漏数据的前后数据链均完整，可以计算与缺漏数据相近数据的算术平均值作为缺漏数据的替代值；若缺漏数据的前后数据链不完整，选取与其同周期相邻数据的近似值作为缺漏数据的替代值[13]；将待评估的数据中的缺漏数据补充完毕后，使用聚类算法对待评估数据按照类型进行聚类，即采用聚类算法对重复、混乱的数据重新分簇[14-17]。

从所有待评估数据中选取n个不同类型的数据作为聚类算法的聚类中心，分别计算其他待评估数据与聚类中心数据的相似值，通过相似值衡量待评估数据是否与聚类中心数据为同一数据类型。相似度度量数值越小，说明2种数据越相似。相似度计算过程如下：

(1)

其中，sim(x,y)为相似度度量，x为聚类中心数据，y为待聚类数据，‖x‖是聚类中心数据的模，‖y‖为待聚类数据的模。将数据分配至与其相似度最高的聚类中心所在簇中，完成数据聚类[18]。在完成对所有待评估数据的聚类分簇后，对聚类中心进行迭代处理，即在聚类簇中重新选取聚类中心，再次计算簇中数据与新选取的聚类中心的相似度，重新进行分簇[19-20]。反复上述过程，直至不再出现新的分类簇。采用聚类算法对待评估数据进行聚类的流程如图1所示。

若待评估数据的类型为随机数据时，需剔除随机型数据的奇异值。假设随机数据的误差为σ，若随机数据满足下式关系，则可判定该随机数据为非奇异值[21]：

-3σy3σ

(2)

当待评估数据的类型为周期性数据时，需对周期性数据做平均滑动滤波处理。假设周期数据的长度为m，平均滑动滤波的窗口长度为l，按照窗口宽度对待评估数据进行采样，将得到的数据存放在整体数据队列的尾端，剔除原来队首的数据。随着采样窗口的移动，得到新的长度同样也为m的数据，完成对数据的平均滑动滤波[22]。

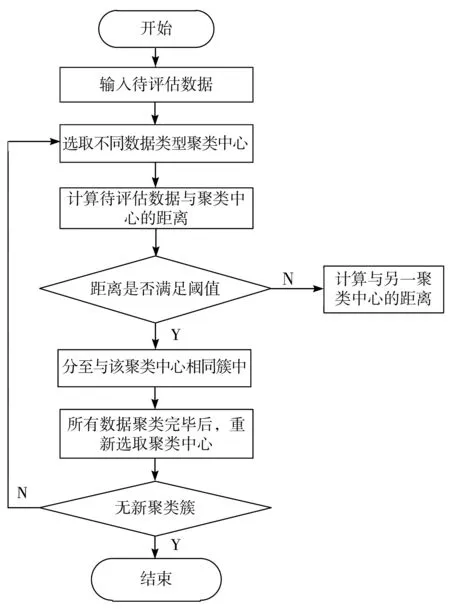
图1 待估数据聚类流程图

由于不同类型数据的量纲不同，需对所有待评估数据做量纲归一化处理，公式如下：

(3)

式(3)中，Xi′为第i类数据Xi经过归一化处理后的数据，maxXi为第i类数据Xi中的最大值，minXi为第i类数据Xi中的最小值。归一化处理过程能够将数据转换为[0,1]区间上的数值，避免了数据量纲对数据可信度评估过程的影响[23]。

在完成待评估数据的预处理后，应用指数分层结构算法建立评估模型。

1.3 应用指数分层结构算法建立评估模型

假设由所有经过预处理后的数据所组成的数据集合为S={X1,X2,…,Xi,…,Xj,…,Xn}，则按照下式计算在某一段时间内待评估数据之间的相关系数：

(4)

dij2=‖Xik-Xjk‖2

(5)

其中，dij2为2个分量之间的欧氏距离，且i维向量的分量Xik满足下式：

(6)

由公式(5)和公式(6)可得到2个分量之间的超度量距离为：

(7)

定义超度量距离为上述的欧氏距离满足数据评估的拓扑结构，即：

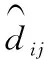
(8)

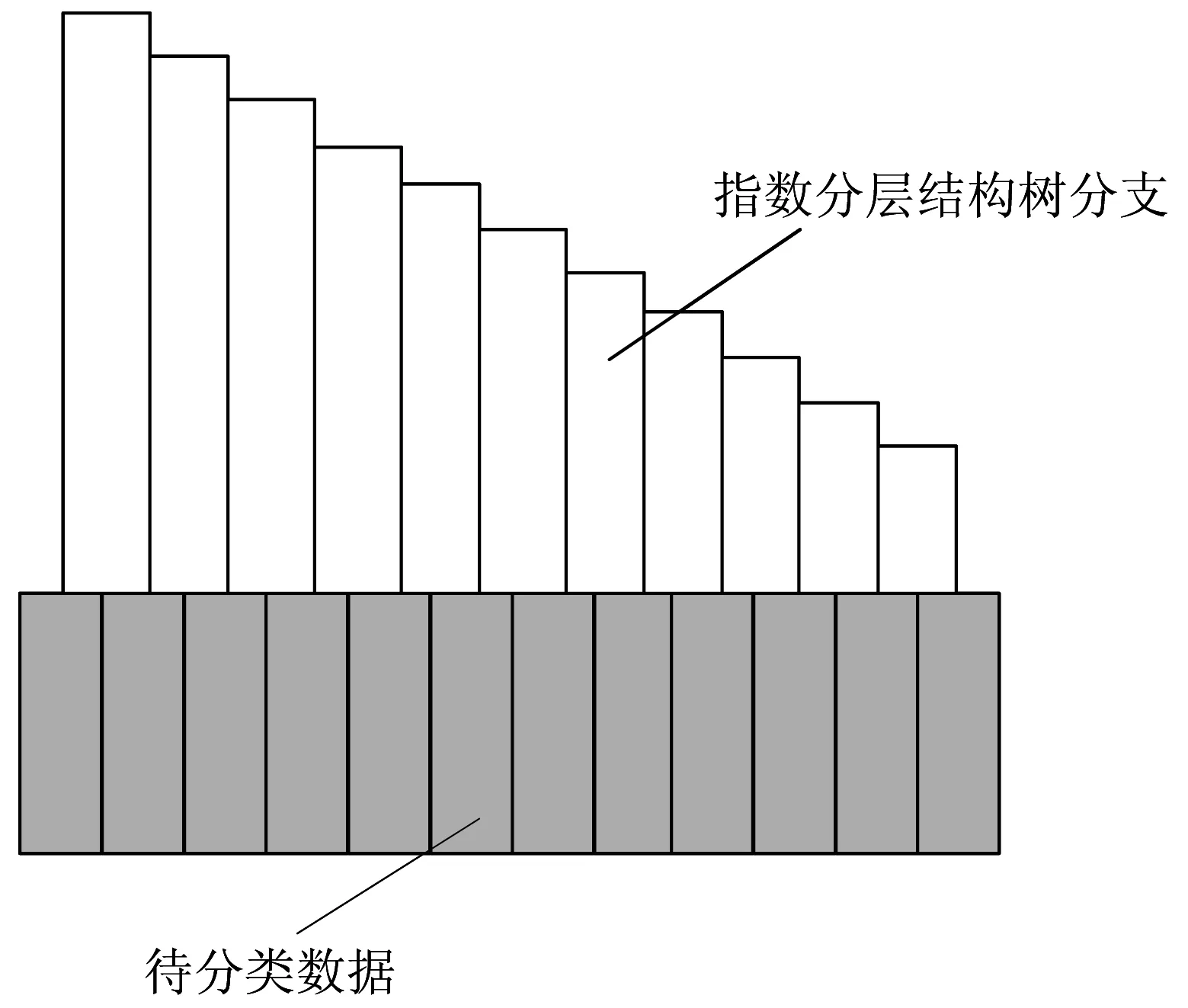
图2 亚超度量空间生成树

在亚超度量空间中，生成树会与经过预处理后的无交叉待评估数据序列相对应，生成了指数分层结构树，根据生成的指数分层结构层次评估树，结合数据可信度评估指标体系，可建立数据可信度判断矩阵。根据评价指标体系中每一指标的权重系数，完成指标的两两比较，并按照表2所示，对指标进行具体赋值。

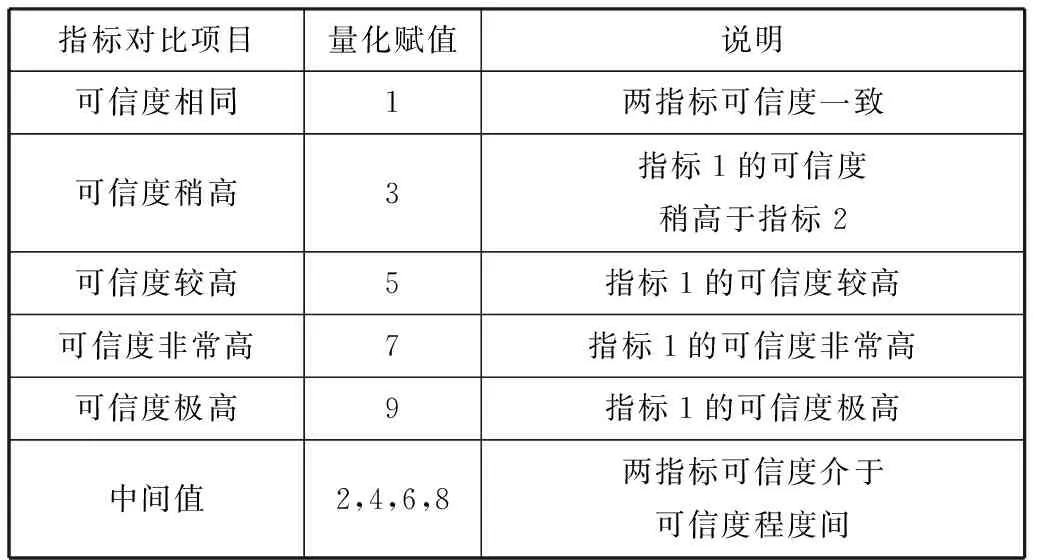
表2 可信度赋值表

在亚超度量空间中，根据可信度矩阵对待评估数据重新映射处理，即：将待评估数据中可信度较高的数据以及与其超度量距离较近的数据判定为可信度高；若与可信度较高数据的距离较近的数据其本身的可信度较低，则不判定该数据的可信度。直至所有待评估数据可信度评估完成后，按照相关系数，再次判定在可信度阈值内的数据可信度，输出待评估可信度的数据结果。至此，完成了基于指数分层结构算法的数据可信度评估。

2 模型测试与结果分析

本文通过实验来验证所提的基于指数分层结构算法的数据可信度评估模型的有效性。为保证实验结果的有效性，将基于D-S理论的多源数据可信度评估模型[8]和基于聚类云模型的小样本数据可信度评估模型[9]作对比。

2.1 测试内容

实验采用数据分类适应性和数据查全率作为验证指标。在对数据可信度进行评估时，评估模型的分类适应性和数据查全率越高，表明评估效果越好。

2.2 测试准备

测试实验环境如表3所示。

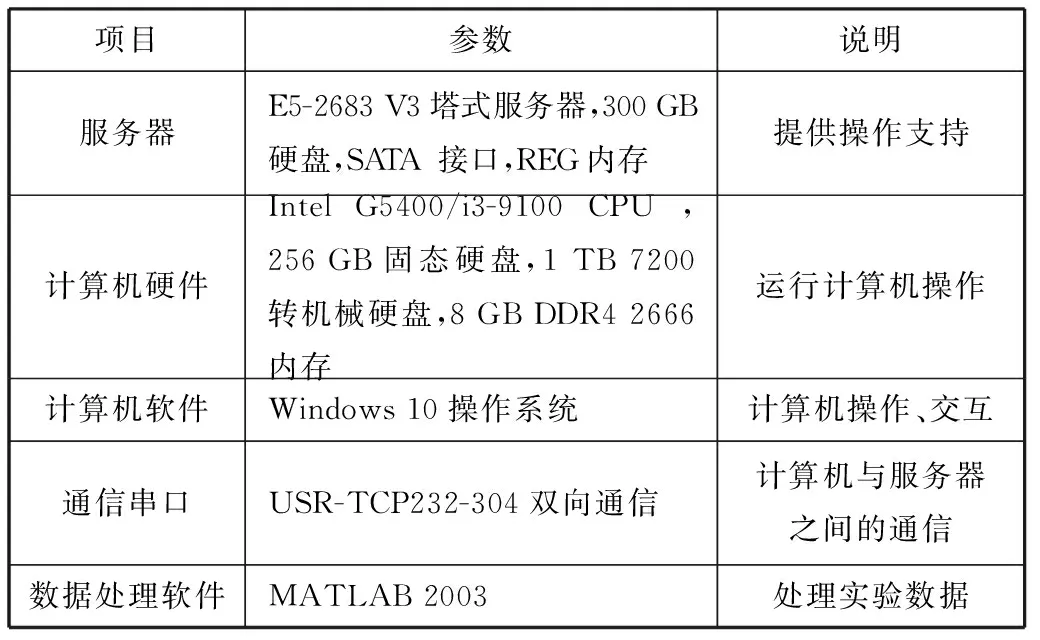
表3 模型性能测试实验环境

实验所用数据的具体类型及参数如表4所示。

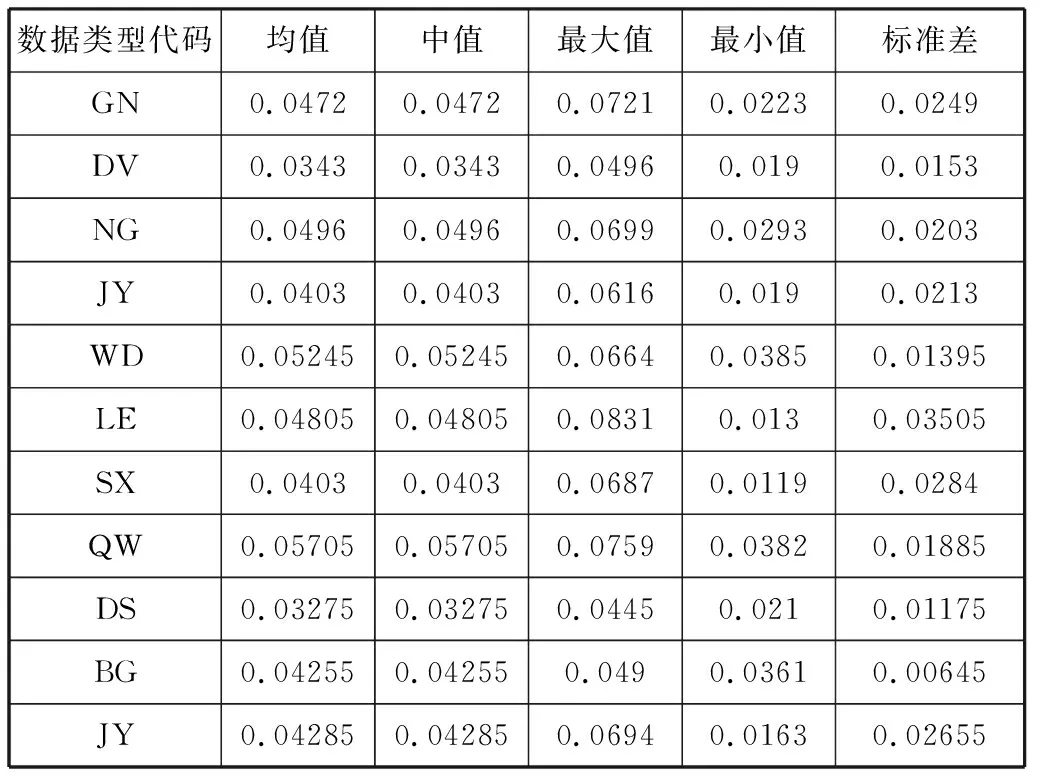
表4 测试数据类型及参数

实验准备完毕后，严格控制除实验变量外的其他实验条件保持相同，完成对测试组和对照组可信度评估模型的性能对比。

2.3 测试结果及分析

数据分类适应性测试结果如图3所示，图中的圆点为数据分类适应点。

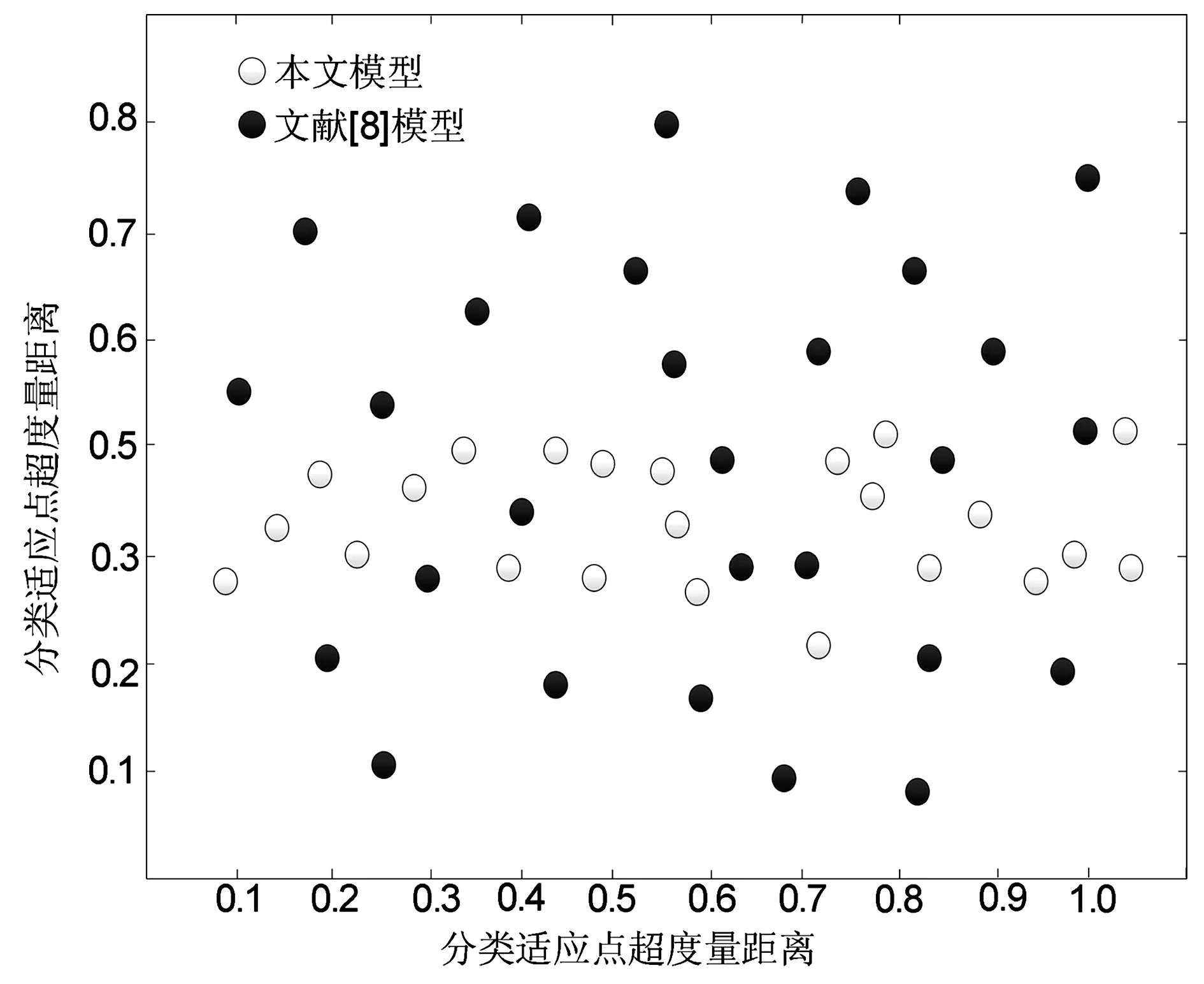
图3 分类适应性对比图

分析图3可知，使用本文模型对数据可信度进行评估时，模型的分类适应数据点较为集中，说明该模型分类适应性较高，使得数据点间距离较近，且本文模型的分类适应数据点不仅分布集中，而且数据点间距离均较小。使用文献[8]模型对数据可信度进行评估时，模型的分类适应数据点分布较为分散，说明该模型的分类适应性较差，使得数据点间距离较远。综上，相比传统的数据评估模型，基于指数分层结构算法的数据可信度评估模型具有较高的分类适应性。

测试不同模型的数据查全率，结果如图4所示。

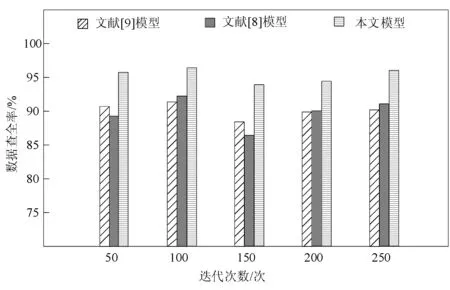
图4 不同模型数据查全率对比

分析图4可知，与2种传统模型相比，利用本文模型对数据可信度进行评估时，数据的查全率较高，整体保持在95%上下，能够说明本文模型对数据的检索能力较强，评估范围更为全面。

3 结束语

为了进一步提高数据资产管理的有效性，本文设计了一种基于指数分层结构算法的数据可信度评估模型。在构建数据可信度评估指标体系的基础上，利用聚类过程对数据进行预处理，并引入指数分层结构算法对数据可信度进行评估。通过与传统的评估模型对比，验证了该模型的分类适应性较强、数据查全率较高，具有更为优越的使用性能。