老年人过街比例与信号交叉口行人过街速度设置研究

张惠玲，奚邦顺

(重庆交通大学，a.山地城市交通系统与安全重庆市重点实验室；b.交通运输学院，重庆400074)

0 引言

我国已进入老龄化社会，老年人参与交通出行的比例越来越高。据统计，老年人交通出行方式中，步行比例为58.3%[1]。老年人随着年龄增加，其视觉、听觉、反应速度等认知加工能力及身体健康状况会呈现出逐渐衰退的趋势，表现出老年人的步行能力及反应速度等特征远弱于中青年人，尤其针对交通情况较为复杂且交通信息设置较为繁杂的信号交叉口，而对老年人步行过街速度考虑不足，将直接导致老年人在信号交叉口的事故频发[2]。国内外学者针对老年人过街主要侧重速度的统计和分析：Duim 等[3]调查统计有97.8%的老年人过街速度低于推荐设置值1.2 m ⋅s-1；Coffin 等[4]建议在老年人较多的地区采用1 m ⋅s-1作为设计速度；HCM2010[5]中建议在老年人比例超过20%的地区，行人过街设计速度设置为1 m ⋅s-1，且随着老年人比例增加，该值继续降低；裴玉龙等[6]认为在老年人活动频繁的地区应对过街设计速度进行调整。上述研究对信号交叉口老年人过街速度进行了调查和分析，但对过街速度设置时老年人混入比例阈值分析缺乏科学依据；另外，针对不同老年人混合比例和不同行人流量下对行人过街速度的影响分析也缺乏系统分析。随着老年人在步行交通中比例逐步增加，老年人在信号交叉口过街需求急需展开系统的分析和研究。

考虑行人流量及老年人比例均会对行人速度产生影响，本文界定年龄在60岁及以上为老年人，利用行人流量与服务水平关系，借助实际采集数据标定后的仿真平台得到不同服务水平下不同老年人比例混入情况时的行人速度数据，并通过主成分分析方法对不同服务水平和老年人混入比例下的行人速度进行分析，应用未知拐点模型，分析不同老年人混入比例下信号交叉口行人过街速度设置情况。

1 老年人行为特性分析及数据采集

1.1 老年人生理-心理特征分析

受自身生理衰老影响，老年人生理机能逐渐退化，使其对周围环境感知能力下降，导致老年人反应迟缓、行动不便。在过街行为中主要表现为：看不清交通信号标志，启动延迟，步行速度较慢等特征。同时，生理上的衰退给老年人心理带来一定的负面影响，如时间知觉退化。老年人拥有更多的社会阅历，在过街时习惯采取直接经验判断，容易忽视身体素质下降，错误地估计绿灯时间、车辆速度等，造成事故发生。老年人生理、心理上的变化都要求改善行人交通设施，信号交叉口行人信号配时也需考虑老年人的实际情况。

1.2 数据采集及分析

为分析不同行人流量与老年人比例下行人过街步行速度特征，同时考虑到现实中很难控制行人流量及老年人比例，采用VISSIM 仿真软件中的VISWALK模块构筑分析。

1.2.1 调查地点

为提高VISSIM仿真实验精度，行人类型划分、不同类型行人过街自由速度、加速度等核心参数通过人工提取实际数据方式获取。各调查点具体情况如表1所示。

表1 各调查地点的具体情况Table 1 Survey of specific circumstances

1.2.2 行人类型划分

行人类型划分主要取决于行人年龄与性别是否对行人自由速度产生影响。行人自由速度指行人在不受干扰时自由步行的速度，通过实地视频拍摄及后期人工提取获得。初步将行人类型分为中青年人及老年人，其中，中青年人指年龄在18～60岁之间的行人，老年人指60岁及以上的行人，视频中行人年龄的大小及性别由实验员直观判断。

式中：V为行人自由速度(m ⋅s-1)；L为人行横道长度(m)；T为行人通过人行横道时长(s)。

通过式(1)计算及统计得到各类行人速度累计图，其中，老年人如图1所示。表2为行人自由速度统计表。

由表2可知，中青年人步速与老年人相差0.1 m ⋅s-1。分析发现，年龄对行人自由速度有显著性影响(P＜0.05)。其中，中青年男性步速与女性相差0.06 m ⋅s-1，老年男性与女性的步速均为1.08 m ⋅s-1。分析发现，性别仅对中青年行人自由速度有显著性影响(P＜0.05)，故将行人类型划分为中青年男性、中青年女性及老年人3类。

1.2.3 不同类型行人加速度

行人加速度代表行人启动快慢。借用轨迹提取软件对行人过街视频进行虚拟坐标划分和个体行人标定[7]，建立人行横道的二维坐标系提取加速度，如图2所示。表3为行人加速度统计表。

由表3可知，中青年人的加速度远高于老年人，这说明老年人在启动速度上慢于中青年人，老年人达到自由速度需要的时间约为中青年人的2倍。

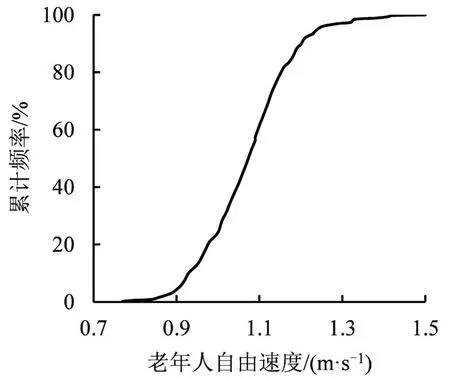
图1 老年人速度分布图Fig.1 Cumulative velocity distribution of the elderly

1.3 仿真实验及结果分析

在VISSIM仿真平台搭建行人过街场景。对每种行人类型，应用相应的速度和加速度数据进行行人交通行为数据校正。实验参考Lam 等[8]研究成果，根据表4设置6 种信号交叉口行人服务水平对应的行人流量。老年人比例在每个服务水平下，从0开始以5%为步长增加至100%。

图2 数据提取区间及虚拟坐标设置Fig.2 Data extraction interval and virtual coordinate setting

行人过街设计速度通常以行人过街的15%位速度作为设定依据，故提取行人15%位速度数值进行分析。通过仿真平台，得到不同行人服务水平下老年人比例与过街行人15%位速度关系，如图3所示。

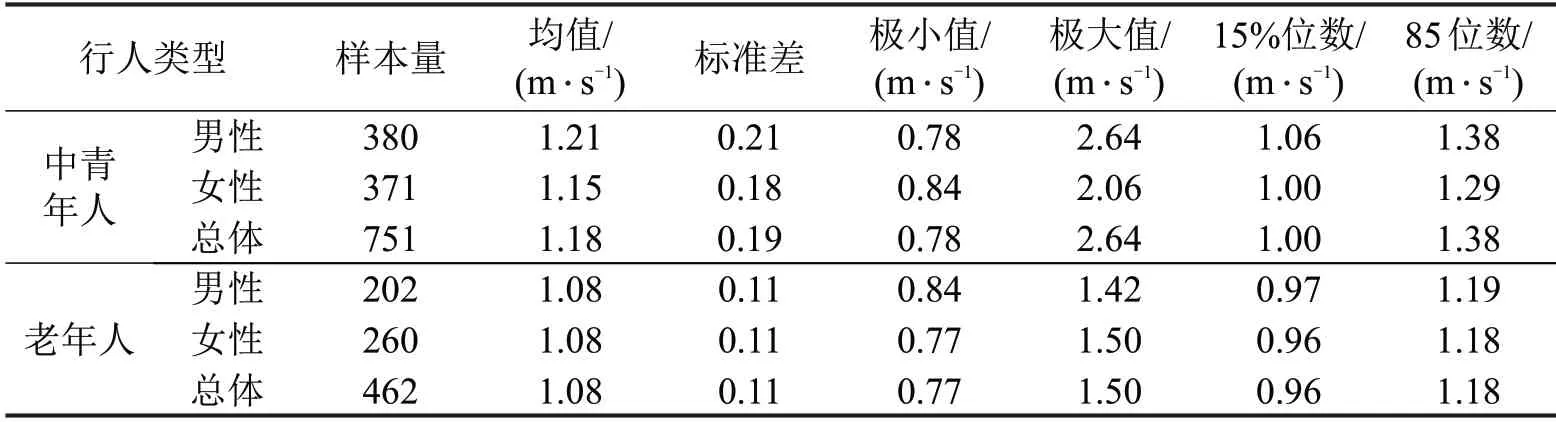
表2 行人自由速度统计表Table 2 Statistics of pedestrian free walking speed

表3 行人加速度统计表Table 3 Statistics of pedestrian maximum acceleration

表4 行人服务水平Table 4 Pedestrian level of service

由图3可知：

(1)行人步速与服务水平、老年人比例有关。相同服务水平下，老年人比例增大，行人步速呈逐渐下降趋势；老年人比例相同时，行人步速随服务水平降低而下降。这是由于老年人步速低于中青年人，老年人比例增加自然会使整体行人步速下降；且当行人流量较大时，处于过街队伍后方的中青年人想要超越老年人将发生横向移动，导致步速减慢。

(2)随服务水平下降，老年人比例与行人15%位速度关系曲线逐渐平稳，即老年人比例对行人步速影响逐渐降低，行人流量对行人步速的影响逐渐增加。

现实中信号交叉口行人流量受天气、时间等诸多因素影响，随机性较大。因此，需要考虑不同行人流量的影响研究老年人比例与过街设计速度的关系。

图3 各级服务水平下行人步行速度与老年人比例关系Fig.3 Relationship between walking speed and older pedestrian ratio at different PLOS

2 老年人过街比例设置阈值分析

2.1 主成分分析模型

主成分分析[9](Principal Component Analysis，PCA)是一种利用正交变换，将原本多个相关的变量指标转化为少数几个独立的新变量指标的统计分析方法。

设有n个样本，每个样本由p个指标描述，得到原始数据矩阵为

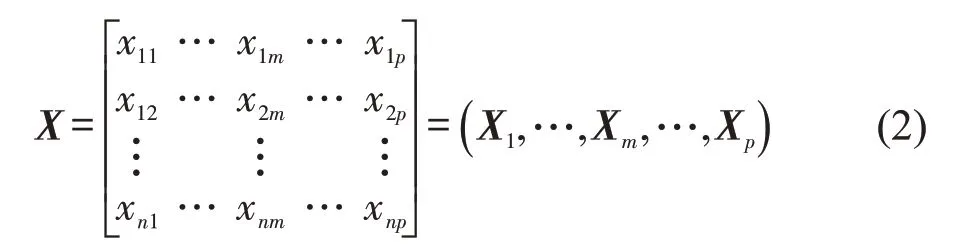
式中：Xm=(x1m,x2m,…,xnm)Τ，m为列索引，m=1,2,…,p。

用矩阵X的p个向量X1,…,Xm,…,Xp进行线性组合得到

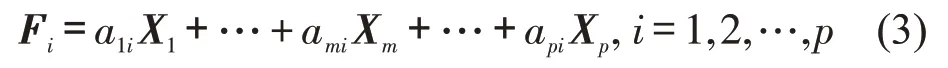
式中：i为向量X1,…,Xm,…,Xp线性组合中的第i种；a1i,…,ami,…,api为线性组合系数，计算公式为

式中：cov(Fi,Fj)为Fi与Fj的协方差；j为向量X1,…,Xm,…,Xp线性组合中的第j种。

将得到的Fi根据方差进行排序，即

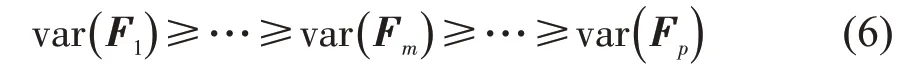
由式(6)确定的F1,…,Fm,…,Fp分别被称为第1主成分，…，第m主成分，…，第p主成分。主成分之间包含的信息互不相关，这样便可用较少的主成分代替原始指标分析问题，通过加权算术平均确定综合评价值，即

式中：λ1,…,λm,…,λp为F1,…,Fm,…,Fp的特征根；f为综合评价值。

2.2 分析步骤

Step 1 建立原始矩阵X。结合仿真平台得到的数据，共有6 个服务水平，每个服务水平下老年人的比例有21 种，故p=6 ，n=21，xnm为m级PLOS 下老年人比例为0.05(n-1)时对应的行人15%位速度，将相应的数据代入式(2)得到X。

Step 2 标准化处理X。对于行人尤其老年人而言，通常希望拥有充足的绿灯时间过街，即过街设计速度越低越好，故采用极差法中负向指标标准化，即

式中：x′i为标准化后指标值；xi为原始指标值；M为该指标下最大的原始指标值；N为该指标下最小的原始指标值。

Step 3 bartlett球形检验与KMO检验。bartlett球形检验得到相关系数矩阵与单位阵有显著差异(p＜0.05)，KMO 检验得到KMO 值为0.847，两者表明，X适合作因子分析。

Step 4 计算主成分及方差。通过式(4)和式(5)确定式(3)中的组合系数，并根据式(6)排序，得到总方差解释表，如表5所示。

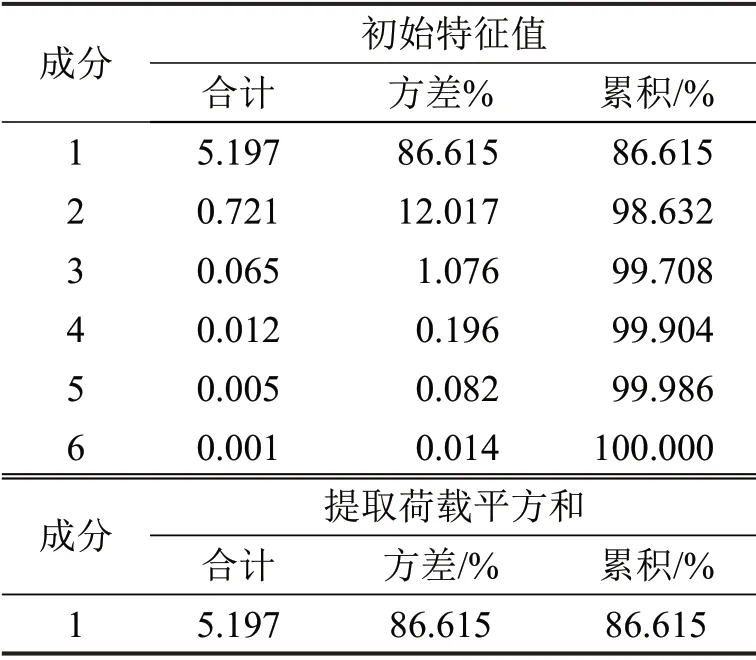
表5 总方差解释表Table 5 Total variance explained

由表5可知，第1 主成分的方差占比达到86.615%，表明信息利用率已达到80%以上，所以仅提取一个主成分矩阵，该主成分的线性组合系数如表6所示。

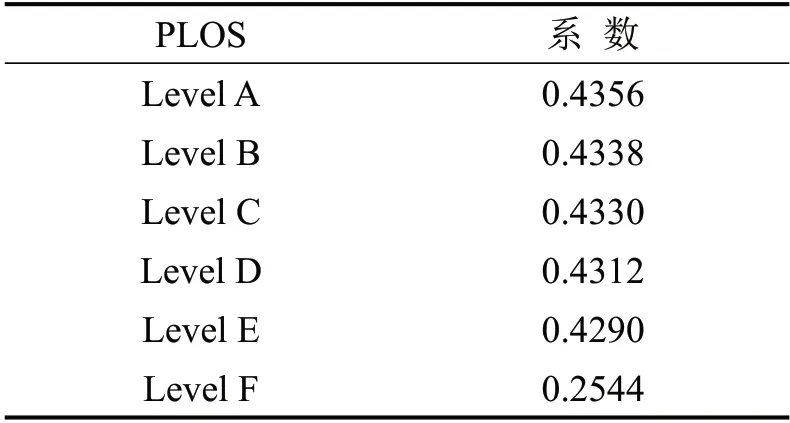
表6 线性组合系数Table 6 Linear combination coefficient

归一化处理表6数据，得到指标集(Level A，Level B，Level C，Level D，Level E，Level F)对应的权重向量ω=(0.1802，0.1795，0.1791，0.1784，0.1775，0.1053)。可以发现，当服务水平从E到F级时，老年人比例对行人步行速度的影响程度骤降。这是因为行人流处于饱和状态时，行人无超越空间，只能跟随过街队伍前面的行人行走。

式中：Y为加权后的数据；X为仿真数据；ω为权重向量。

通过式(9)得到考虑行人流量影响下的老年人比例与行人15%位速度(即设计速度)关系，如图4所示。

由图4可知，随着老年人比例增加，行人过街设计速度下降速度经历由慢到快再到慢的变化过程，且二次拟合结果优于线性拟合，两者关系呈非线性相关。因此，需要找出两次发生变化的拐点，作为老年人比例与行人过街速度设计阈值。

2.3 老年人比例与行人过街速度设计分析

当两组数据之间存在较为明显的分段线性变化关系时，可采用未知拐点的线性模型[10]对其进行拟合。未知拐点的线性模型原理为

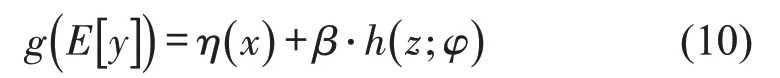
式中：g(E[y])为对任意变量y的线性拟合；η(x)为模型中变量x的线性项；h(z;φ)为模型中带参数φ的变量z的非线性项；β为模型中h(z;φ)的参数。

图4 行人步行速度与老年人比例关系Fig.4 Relationship between pedestrian walking speed and older pedestrian ratio

h(z;φ)在初始值φ(0)处一阶泰勒展开后，得到

式中：h′(z;φ(0))是h(z;φ)在φ(0)的一阶导数。

此时，所有变量都取决于φ(0)，故在设置好初始值φ(0)后，可使用最大似然估计法对模型进行迭代计算。

结合本文数据，拟合函数模型为

式中：y为行人过街设计速度(m ⋅s-1)；z为老年人比例(%)；φ为拐点(%)；α为z ＜φ时的斜率；ϕ为φ两边的斜率差；(z-φ)+为z≥φ时的非线性项。

若存在拐点φ，则ϕ≠0，得到线性方程组。利用麦夸特法和通用全局优化法对模型进行优化，再迭代计算，模型收敛后得到结果，如图5所示。

拟合结果评价参数R2=0.998，表明拟合函数能够较为真实地反映出两者关系，将函数拐点，即老年人比例为21%、41%作为调整行人过街设计速度阈值。结合本文分析，得出其速度设置值分别为0.94 m ⋅s-1和0.86 m ⋅s-1。

图5 数据拟合结果Fig.5 Data fitting results

2.4 实例验证

为验证研究成果的应用情况，实地调查不同类型信号交叉口，具体情况如表7所示。

通过人工提取，统计得到行人速度累计分布图，如图6所示。

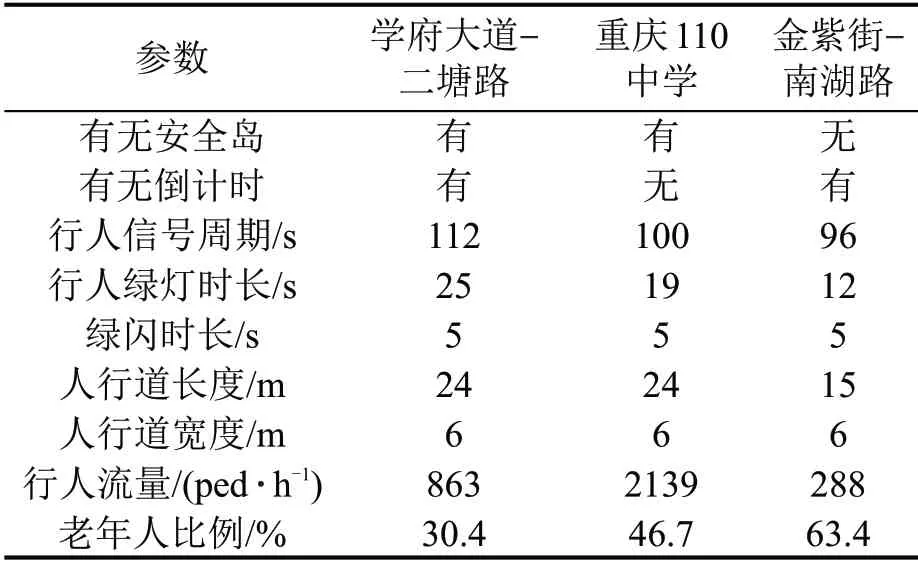
表7 不同类型信号交叉口的具体情况Table 7 Specifics of different types of signalized intersections

图6 不同类型信号交叉口行人数据Fig.6 Pedestrian data for different types of signalized intersections

将被调查行人的15%速度与本文分析的推荐值进行对比，结果如图7所示。

由图7可知，不同类型信号交叉口，在不同老年人比例下，调查得到的实际行人过街15%速度和本文研究的推荐设计速度相接近，表明本文研究成果与实际较吻合。

图7 实际与推荐值对比Fig.7 Comparison of actual conditions

3 结论

针对信号交叉口老年人不同比例下的过街速度设置情况，通过PCA 和未知拐点模型综合分析过街老年人比例在不同服务水平下对行人过街速度的影响程度。建议：信号交叉口过街老年人比例在(21%，41%)时，行人过街设计速度设置为0.94 m ⋅s-1；若超过41%时，可进一步调整为0.86 m ⋅s-1，为老年人过街需求较多的信号交叉口提供了改善措施。由于行人过街行为及信号交叉口的复杂性，本文只研究了中青年人及老年人独自过街的速度特性。