基于模拟退火-自适应布谷鸟算法的城市公交调度优化研究
赖元文,张杰
(1.福州大学,土木工程学院,福州350116;2.宁德师范学院,信息与机电工程学院,福建宁德352100)
0 引言
公交调度作为优化公交运营效率,增大公交出行吸引力的重要手段,具有较大提升潜力,国内外诸多学者对公交调度优化模型及求解算法展开研究。TANG等[1]通过公交车历史轨迹估算公交行程时间,建立以实际出行时间最短为目标,车内容量限制为约束条件的公交调度模型。NAM 等[2]从环保角度入手,建立以燃油消耗、碳排放为指标的环境成本最小公交调度模型。王凤刚[3]考虑驾驶员成本,建立以司机数量最少的最小费用流公交调度模型。SONG 等[4]提出加入基因重组的改进遗传算法,求解公交调度问题。陈少华[5]设计改进邻域搜索模拟退火算法用于公交发车时刻表优化。张莉[6]针对遗传算法“早熟”特点,在过程中加入退火操作,寻找发车时刻全局最优解。
国内外学者在公交调度模型构建上,假设条件较多,且与调度线路实际客流特征联系较少。在模型求解算法上,改进传统算法占多数,新兴算法在公交调度中的应用还存在较大研究空间。因此,本文提出一个公交调度优化模型,并设计一个启发式算法对模型求解,将线路客流特征数据应用于公交调度优化模型构建,加强模型与实际客流联系的基础上,减少模型假设条件,并采用改进新兴仿生群算法-布谷鸟算法求解模型,加强寻优效率,以期得到更好的模型优化效果。
1 考虑客流特征的公交调度模型构建
1.1 建模思路
不同时段客流需求不同,构建与线路实际客流特征相关的公交调度模型更具实用性。因此,考虑如下因素:
(1)发车时段
乘客不同时刻出行需求不同,对客流量相似时段进行整合,将结果应用于公交调度发车时段划分,优化公交资源利用率。
(2)站点上、下客量
现有公交调度模型,多将站点无滞留乘客作为假设条件。本文结合客流特征及车辆核定载客人数,计算车内空余可乘车人数,与等车人数对比反映站点滞站人数,减少模型假设条件;同时,通过车内人数设计约束条件,界定平均满载率,防止载客量过低,浪费公交资源。
(3)区间载客量
定义经过某断面所有班次车内人数为该条线路在该研究时段的区间载客量,计算方法为在该断面前所有站点上车人数减去下车人数。区间载客量反映该时段车内乘客拥挤程度,进而求出不同拥挤程度下所需发车次数。
(4)乘客舒适性
每个人与陌生人都存在一定的心理安全间距,当间距小于可接受范围,人会产生烦躁、不安、排斥等心理抗拒现象。因此,当公交车内过于拥挤时,人与人间距小于心理安全间距,乘客会产生心理抗拒现象,导致公交吸引力降低。
1.2 模型构建
(1)假设条件
①出行人员到达站点规律服从均匀分布,不会被其他线路车辆干扰;
②研究线路所有车辆均依据运营计划定时出站、到站运行;
③相同研究时段内发车间隔相同。
(2)目标函数
对于公交公司,利益主要与收入挂钩,将运营成本作为优化目标;对于乘客,搭乘公交希望在节约成本的同时有良好的出行体验,采用乘客满意程度作为优化目标。
①公交公司运营成本
将班次运行带来的资源消耗费用与人工费用统一为车辆每行驶1 km 产生的费用,公交公司全天运营成本为

式中:Cb为一天内公交公司运营总成本(元);Cv为研究线路公交车运行1 km产生的费用(元);L为研究线路总长度(km);Tj为j时段总时长(min);tj为j时段的发车间隔(min);J为发车时段总数,发车时段数集合M={1 ,2,…,J} ,j为第j个研究时段。
②乘客满意程度
乘客在公交出行中,对出行体验感知最大的部分为站台等车时间及乘车过程中车内环境舒适程度。
将乘客等车时间造成的不满意程度量化为乘客等车过程中损失的价值成本。对于正常上车无滞站乘客,乘客等车成本通过线路全天所有班次乘客等车时间总成本进行度量。根据假设条件,每个乘客平均等车时间等于泊松分布期望值,平均1 min等车状态下损失成本由城镇居民人均可支配收入确定,全天候等车成本为

式中:Cp为研究线路全天所有班次乘客等车时间总成本(元);Cw为每位乘客1 min等车状态下的损失成本(元⋅min-1),根据城镇居民人均可支配收入确定;I为所研究线路总站点数,站点数集合N={1 ,2,…,I},i为线路上第i个站点;Pij为第j个时段下位于i站点等车人数(人)。
乘客乘车过程舒适度与公交调度相关的是车内拥挤程度。因此,通过乘客在车内感受到的拥挤程度对自身舒适感差异,定义乘客在乘车过程中因拥挤造成的价值惩罚为拥挤成本。
用立席密度表征乘客活动空间,通过确定乘客开始感受拥挤时立席密度下限值及乘客无法忍受拥挤情况时的上限值及公交车有效站立面积,计算拥挤成本。当乘客未感知到拥挤,不产生拥挤成本;当乘客开始感受拥挤时,拥挤成本随乘客数量增加而变大。当车内拥挤程度超过乘客忍受极限,拥挤成本惩罚值变为无穷大,即

式中:Bpd、Bpu分别为公交车内载客人数引起乘客产生不适感时下限人数,不适感难以忍受的上限人数(人);V为公交车辆有效站立面积(m2);Vd、Vu分别为乘客开始感受到拥挤的立席密度下限值、乘客无法忍受拥挤情况的上限值(m2)。
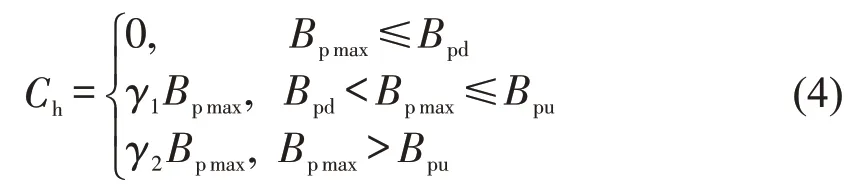
式中:Ch为乘客拥挤成本(元);Bpmax为该公交车上人数最多时的人数(人);γ1、γ2为两个状态下对应的拥挤度系数。
公交决策人员在权衡双方利益时需要从不同角度考虑,通过赋予权重的方式实现,即

式中:Z为目标函数;z1、z2为加权系数,z1、z2>0且z1+z2=1。
1.3 约束条件及处理
模型满足以下约束条件:
(1)收支平衡约束
在调度时至少要保障公交公司收入大于支出。
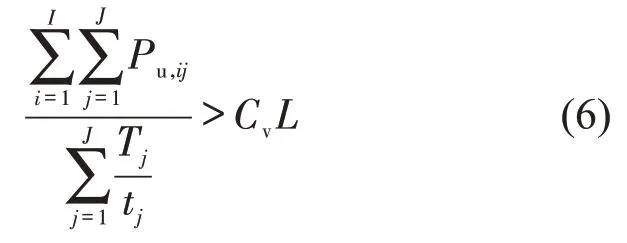
式中:Pu,ij为j时段i站点上车人数(人)。
(2)载客人数约束
为避免出现空载,需保证车辆平均满载率不低于最低满载率要求。同时,为保障乘客舒适体验,乘客能够一次上车避免滞留,需保证车内最大乘车人数小于额定载客人数。

式中:Pcˉ为一趟班次平均满载率;Pcmin为一趟班次平均最小满载率;Pr为研究线路车辆额定载客人数(人);Pc,i为一趟班次在第i个站点时车内载客人数(人)。
通过惩罚函数将约束条件转化为带惩罚系数项加入目标函数,即

式中:minZ′为带惩罚项的新目标函数;δ1、δ2、δ3为惩罚系数,取值大于0,根据实验确定。
2 模拟退火-自适应布谷鸟算法设计
布谷鸟算法[7]具有参数少、局部搜索能力强的优点,但其搜索步长为定值,并且布谷鸟莱维(levy)飞行习性造成长距离步长占比较少,容易陷入局部最优解,成为算法短板。
2.1 算法设计
(1)改进算法步长
构造步长值先大后小的自适应步长,算法执行前期,通过跨度大的步长扩大搜索范围;算法执行后期,步长变小,在全局最优范围内精细化求解,表示为

式中:Tmax为总迭代次数;tap为当前迭代次数;α(t)为当前迭代次数下步长值;αmin为最小步长;αmax为最大步长;t为迭代次数。
(2)增加退火操作
引入模拟退火算法中退火阶段操作,使布谷鸟算法在更新鸟窝位置时存在接受较差解的概率,增加全局寻优概率。退火过程为
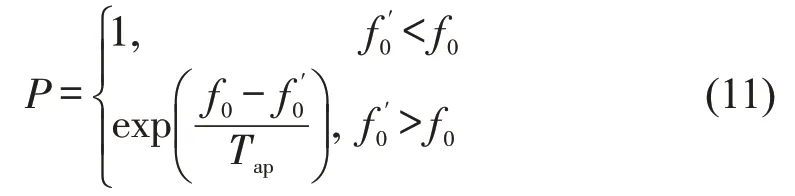
式中:f0为当前最优解x0对应目标函数值;f0′为新解x′0所对应目标函数值;Tap为当前状态温度。
2.2 算法流程
模拟退火-自适应布谷鸟算法步骤如下:
Step 1 设置算法参数。包括:鸟巢个数N、发现概率Pa、迭代精度或次数Tmax、初始温度T0、退火系数Tα、最低温度Tmin、扰动次数Tk等参数,并初始化种群,计算相应函数值,作为当前最优解。
Step 2 根据式(10)更新鸟窝位置,计算更新后鸟窝函数值,和上一代鸟窝函数值对比,保留当前最好鸟窝。
Step 3 将较差一组鸟窝进行模拟退火操作,若新解对应函数值比现解更好,则更新当前最优解;否则,依照概率接受新解,并让当前温度在退火系数Tα下执行退火操作并更新当前最优解。
Step 4 对每个鸟巢,任选其他2 个不同鸟巢,按照文献[7]位置更新公式计算。当新解比旧解好时,更新当前最优解。
Step 5 记录当前最优解,若满足停止条件,输出最优解;否则,返回Step 2继续寻优。
2.3 仿真实验
选取3个算法测试常用标准函数,验证改进算法寻优性能,选取函数为

式中:x1、x2、xi为自变量;d为自变量x的总个数。具体参数如表1所示。
迭代结果如图1所示。图中,SA为模拟退火算法(Simulated Annealing),CS 为布谷鸟算法(Cuckoo Search),SA-ACS 为模拟退火-自适应布谷鸟算法(Simulated Annealing-Adaptive Cuckoo Search)。由图1可知,模拟退火-自适应布谷鸟算法未陷入局部最优解,在较小的迭代次数下逼近全局最优解,具备求解全局最优的能力,传统布谷鸟算法的缺陷得到改善。因此,采用改进的模拟退火-自适应布谷鸟算法对公交调度模型优化是可行的。

表1 测试函数属性Table 1 Test function properties
3 模型应用与验证
福州市125 路公交线路途经学校、商业区、工业区、行政区、大型居民区、医院,以及风景区,且与地铁1 号、2 号线路重复率低,涵盖各种出行目的,因此,选取该线路作为实例研究。

图1 迭代结果Fig.1 Iterative results
3.1 线路客流特征
(1)客流区间划分
以125路2020年10月15日-17日,即周二-周四客流为例,挖掘乘客刷卡数据获取客流数据,各时段平均客流如图2所示。
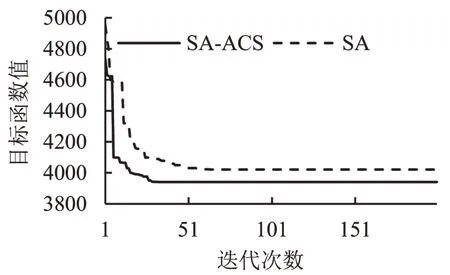
图2 125路全天客流Fig.2 No.125 bus line throughout passenger flow
由图2可知,125 路上、下行上车客流趋势相近,故选用上行方向研究。
125 路运营时段为6:00-21:00,将运营时间分为:6:00-7:00,7:00-8:00,…,20:00-21:00,采用Fisher 最优分割法对客流进行处理,得到误差函数变化,如图3所示。
由图3可知,当分类数取7时,误差值变化已经非常小,故分类数取7 作为客流峰值划分区间数。125路客流区间划分如表2所示。

图3 误差函数曲线Fig.3 Error function curve

表2 125路客流区间划分情况Table 2 Specific situation of section division of No.125 bus line passenger flow
(2)线路客流特征分析
125 路全天各站点客流情况如图4所示。可知,从首站开始,直到第19 个站点,下车人数才逐渐高于上车人数,中途站点车内载客人数一直处于较大状态。若发车频率低,可能造成第12 个站点至第18 个站点区间车内乘客拥挤程度较高,导致乘客舒适度较低。
早高峰时段各站点上、下客及区间载客量情况如图5所示。
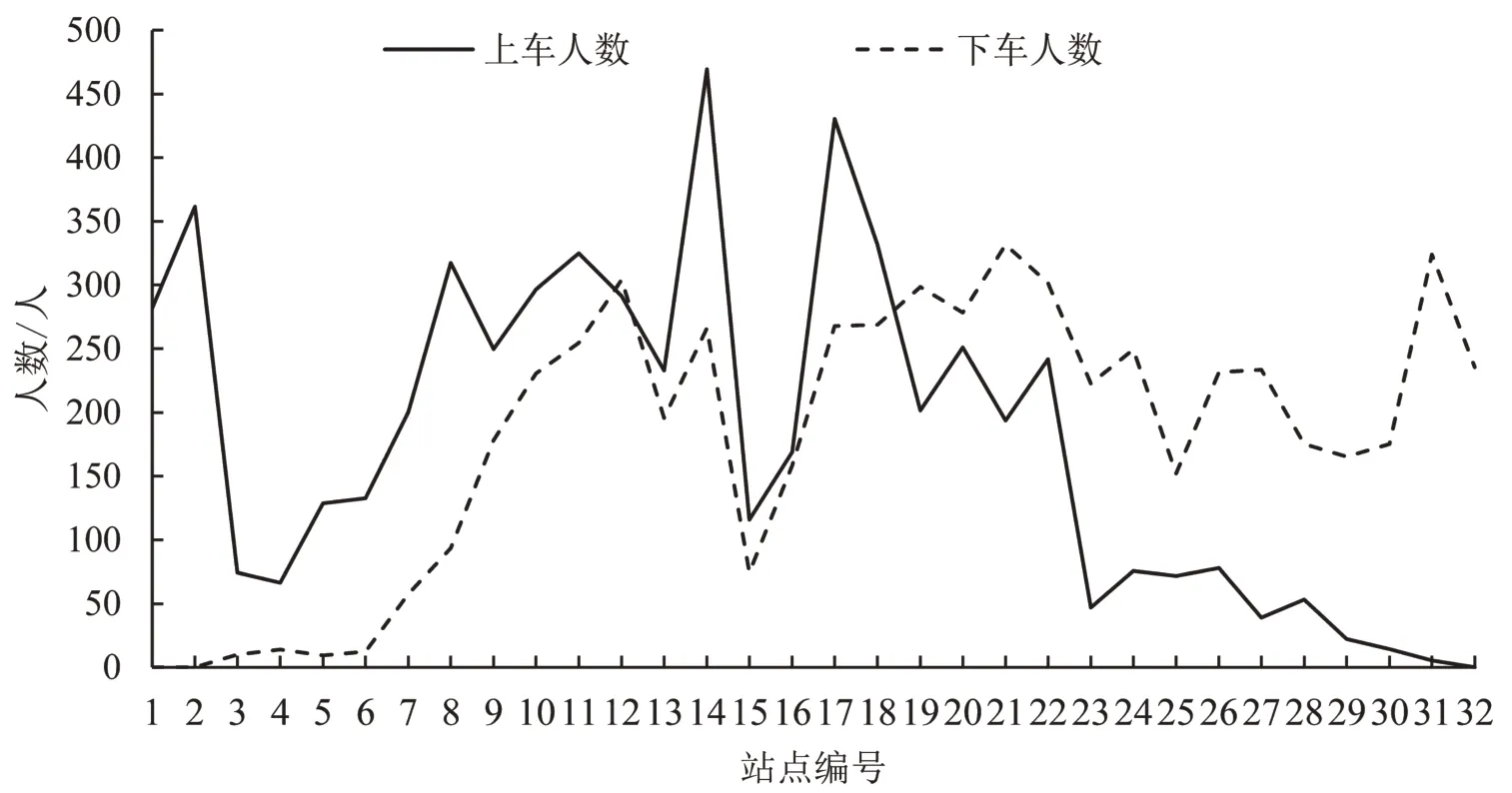
图4 125路全天各站点上下客情况Fig.4 No.125 bus line throughout day on and off at each station
由图5可知,早高峰时段居民出行量大,前几站上车人数多,较早产生拥挤情况,且拥挤过程持续时间长。因此,考虑乘客满意程度,关注车内最拥挤时客流峰值,保证最拥挤站点的乘客舒适度在乘客可接受范围内。
3.2 模型求解及分析
(1)模型及算法参数输入
每公里公交车辆产生费用Cv、公交车有效站立面积V、座位数S由公交公司提供,结合文献[8],立席密度下限值、上限值分别为0.250、0.125,通过该取值计算得出Bpd、Bpu,Cw参照2019年福州市城镇居民人均可支配收入,最低平均满载率要求为座位数的70%,故Pcmin取15人,惩罚系数δ1、δ2、δ3经试验均取1000。经反复试验,步长更新参数λmin取0.005,具体参数及取值如表3所示。
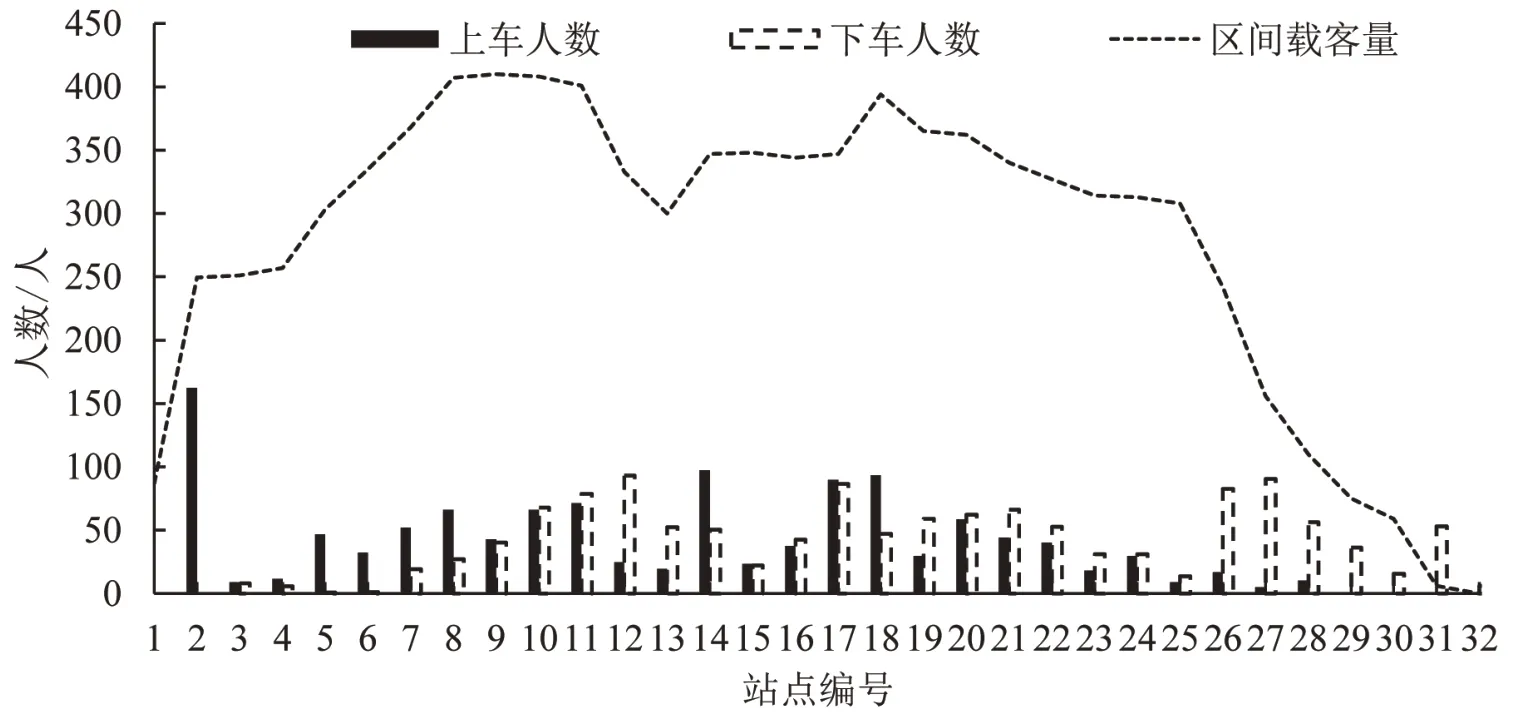
图5 早高峰时段各站点上、下客及区间载客量Fig.5 Loading and unloading and carrying capacity of morning peak period
(2)求解结果分析
通过调整权重,分析侧重公交公司、乘客不同利益方情况下发车情况,按表4方案进行仿真实验。仿真结果如表5和图6所示。
由图6可知:
①改进模拟退火-自适应布谷鸟算法在求解结果及寻优效率上均优于传统布谷鸟算法及模拟退火算法,模拟退火算法虽然在反复迭代下逼近全局最优解,但寻优效率要低于布谷鸟算法,验证了改进模拟退火-自适应布谷鸟算法在算法性能上的优越性。
②将实例仿真结果与实际调度情况相比,125路公交月均发车5479次,上行方向日均发车96次,各时段发车次数对比如图7所示。
由图7可知,不同权重比例下平峰时段发车次数均小于现状发车次数,有效节约资源,验证了算法在求解结果上的有效性。且高峰期发车频率大于其他时期,10:00-16:00 发车次数最少,寻优结果符合实际。
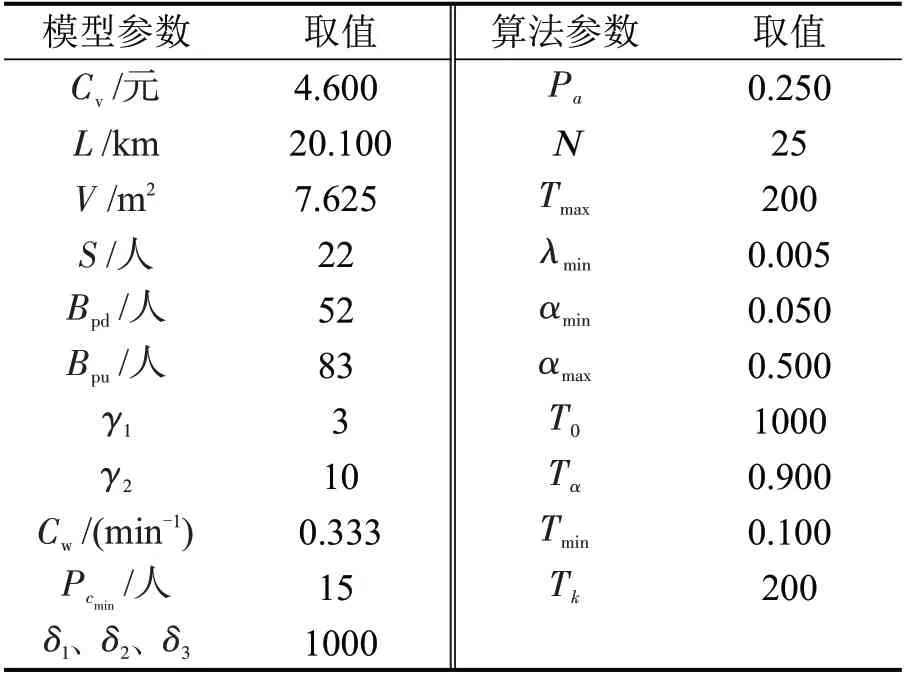
表3 模型及算法参数输入Table 3 Value of model and algorithm parameters

表4 不同权重仿真方案Table 4 Simulation schemes with different weights
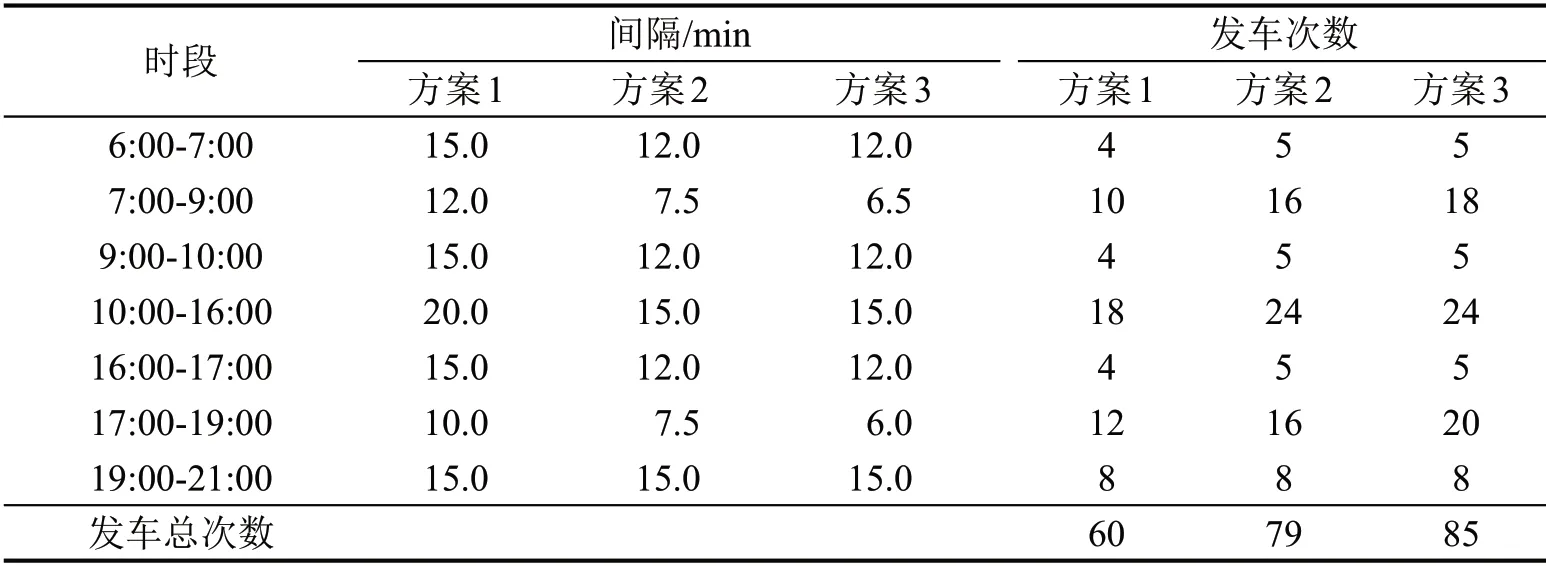
表5 各时段发车情况Table 5 Each time period starts
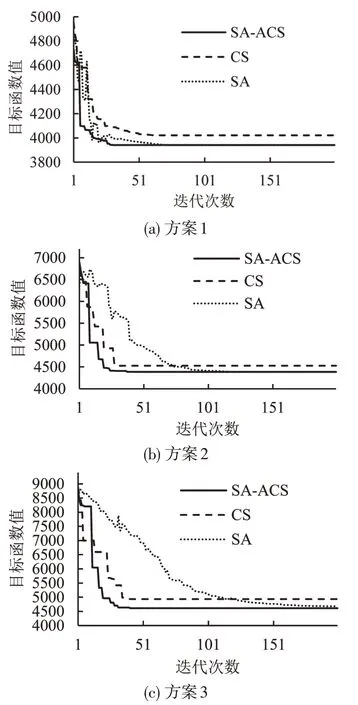
图6 不同权重下的仿真结果Fig.6 Simulation results under different weights
(3)由仿真结果可知,z1、z2取值差异对仿真结果影响较大,当z1大于z2,目标函数更侧重于公交公司利益,公交发车间隔大、发车频率低。反之,发车间隔减小、发车频率增大,目标函数朝乘客利益倾斜。随着发车次数增多,公交公司运营费用不断提高,在进行实际调度时,可根据不同线路实际情况,采用不同权重进行调度安排。

图7 发车次数对比Fig.7 Start times comparison
4 结论
本文以常规公交为研究对象,利用挖掘线路客流特征,减少模型假设条件。在模型指标选取上,创新地考虑了基于乘客心理空间的乘车舒适性,将其转化为拥挤成本进行量化。设计了模拟退火-自适应布谷鸟算法,使算法具备全局寻优能力。以福州市125 路公交为例,求解基于Fisher 最优分割法所划分7 个时段的公交发车间隔,设置3 种不同权重方案对目标函数进行仿真,实验结果表明,不同权重下模拟退火-自适应布谷鸟算法的寻优结果均为最佳,发车次数均小于现状发车次数,并且仿真结果符合实际客流情况,验证了优化模型及算法的可行性。本文仅考虑常规公交调度,如何与城市轨道交通进行协调调度将是未来研究方向。

