双车道公路弯道半径及回旋线长度对转向行为的影响

袁方，杨轸，周雄峰

(同济大学，道路与交通工程教育部重点实验室，上海201804)

0 引言

回旋线是道路平面线形的基本要素，具有使路线平顺、减少横向力突变等诸多优点。有分析指出，回旋线的平面几何特征是影响双车道公路转向行为的重要因素[1]。另一些研究表明，回旋线与双车道公路弯道交通事故存在显著相关性[2-4]。因此，研究双车道公路回旋线设计的合理性有助于提升弯道的安全性能。

Spacek[5]发现，不当的转向行为是影响双车道公路弯道安全的最重要因素，当半径和回旋线长度组合不当时，车辆轨迹与车道轴线的偏差会比较明显，导致驾驶员采取过度的方向修正，因此产生的附加侧向力不利于车辆稳定。Perco[6]认为回旋线长度是造成这种过度修正的主要原因，当回旋线过长时驾驶员在过渡段容易被前方曲线的锐度误导，使得车辆产生较大的侧向偏移，为弥补这种偏差，驾驶员会反复修正方向，回旋线越长方向修正的次数就越多。有分析建议，理想的回旋线长度应和车辆的自然转向行程一致[7]。《A Policy on Geometric Design of Highways and Streets》[8]采纳了这类建议，并推荐以2 s 行程作为自然转向行程的代表值。Said[1]通过自然驾驶实验证明，双车道公路自然转向行程与曲线半径有显著相关性，并建议重新审查《A Policy on Geometric Design of Highways and Streets》中的推荐值。

我国《公路路线设计规范》[9]规定，回旋线参数A应满足R/3 ≤A≤R，但是对半径R在100～3000 m之间的弯道回旋线长度并未做出明确限制，故可以进一步研究并补充优化建议。《A Policy on Geometric Design of Highways and Streets》[8]建议以2 s行程为理想回旋线长度建议值，这与《公路路线设计规范》[9]中“汽车在缓和曲线上的行驶时间不小于3 s”的规定之间存在差异，有必要在我国规范规定的取值范围内，验证回旋线对转向操控的影响。Perco[6]、Said[1]等的研究证明了自然转向行程因曲线半径而异，但并未验证相同半径条件下自然转向行程是否会受回旋线长度影响。此外，也未说明当回旋线长度等于自然转向行程时，驾驶员的操纵行为表现是否良好。

针对以上问题，采用驾驶模拟实验研究双车道公路弯道半径、回旋线长度对自然转向行程及轨迹修正行为的影响。首先，依据我国规范设计双车道公路场景，收集驾驶员在弯道中行驶时的方向盘转角信号；然后，运用小波变换对该信号进行分解，提取自然转向及轨迹修正的相关特征；最后，分析这些特征依半径和回旋线长度的变化规律，并对回旋线的合理长度提出建议。

1 实验设计

1.1 驾驶模拟实验的合理性

驾驶模拟实验具有安全、成本低、变量可控、可重复实验等优点，被广泛应用于驾驶行为研究。Gerard[10]等指出，驾驶模拟实验中车辆纵向控制具有良好的绝对和相对有效性，横向操控具有良好的相对有效性。Wade[11]、毛喆[12]的研究结果表明，模拟驾驶的车速、横向偏移特征与实车行驶无明显差异。因此，用驾驶模拟器研究弯道的转向行为具备合理性。

1.2 实验仪器和数据采集

基于ScaNer Studio 驾驶模拟仿真平台采集车速、加速度、方向盘转角、道路曲率和桩号数据，采样频率设置为50 Hz。其中，方向盘转角数据左转弯时为正，右转时为负。

1.3 实验场景

实验场景设计主要考虑以下几个因素：

(1)《公路路线设计规范》[9]对半径100～3000 m弯道的回旋线长度未作出明确的限制，故据此确定实验道路半径的最小值为100 m。

(2)Perco[5]等研究表明，双车道公路弯道半径大于等于600 m时，车辆的轨迹几乎与车道轴线平行，观察不到明显的转向行为，此时轨迹修正行为与直线路段接近。在平面几何指标较低时，不同半径弯道的转向行为差异才比较突出[1]。因此，确定实验道路半径的上限为500 m。

(3)100 m半径对应设计车速40 km·h-1条件下的一般最小半径，并与设计车速60 km·h-1时的极限最小半径接近(最大超高8%时，极限最小半径125 m)。为尽可能多的提高弯道样本量，回旋线长度下限值取40 km·h-1设计车速对应的回旋线最小长度35 m，最终确定36 种半径、回旋线长度组合，圆曲线和回旋线的长度比为1∶1，如表1所示。因为设计车速40 km·h-1和60 km·h-1的双车道公路车道宽度均为3.5 m，所以36 种组合可以覆盖上述两种设计车速条件下的大多数典型情况。

(4)设计车速80 km·h-1时，平面几何设计指标较高，不同半径弯道之间的转向行为差异不明显，故该设计车速条件未予考虑。

(5)为节约建模开销，从起点至终点方向，所有弯道均为左转向，实验时从终点返回起点即完成右转向测试，每个驾驶员要经过72个弯道路段。

1.4 实验人员及实验过程

公开招募年龄25～45岁的驾驶员15名，男女比例2∶1。实验开始前让每名被试试开一个场景，熟悉后再进行正式实验。实验时，要求驾驶员以接近自然驾驶的状态行驶，从每条道路的起点驶向终点完成左转测试，再按原路返回完成右转测试。

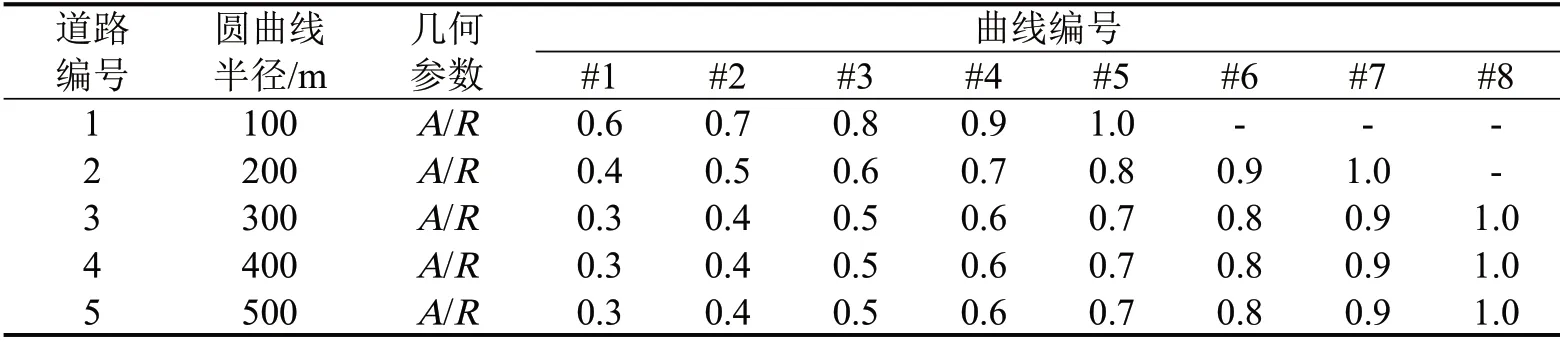
表1 弯道平面设计值Table 1 Horizontal design value of curves

2 方向盘转角信号的小波分析方法

2.1 方向盘转角信号的分量

车辆过弯时，理想的方向盘转角信号沿桩号的变化曲线应与路线曲率沿桩号的变化曲线相一致。但在实际行车中，方向盘转角信号一般由3个分量构成。

(1)低频分量

低频分量l(x)是指方向盘转角信号中接近理想转角信号的部分，它的函数曲线与路线曲率图线的变化趋势基本一致，其中，x为沿道路中线方向的桩号坐标。l(x)可以用来提取驾驶员过弯时的转向起点和转向终点，并计算出自然转向行程。

(2)高频分量

高频分量h(x)是指驾驶员在转向过程中为使车辆保持在车道中心线附近行驶的微调操作。这部分频率较高，期望接近于0，可用来分析轨迹修正负荷与车辆侧向稳定性。

(3)系统噪声

仪器自身产生的噪声信号，频率最高。

2.2 方向盘转角信号的小波分解

为研究自然转向和轨迹修正两种行为，需要将l(x)和h(x)从原始信号中分离出来。分离思路为：先过滤系统噪声实现对原始信号的平滑处理，然后进一步分解信号，分离出l(x)和h(x)。本文采用离散小波变换对方向盘转角信号进行滤波与分解处理。

(1)小波变换原理

小波变换的基本原理为：设ϕj,k为j阶的小波尺度函数，其中，j为伸缩因子，j越大尺度函数的频率越高；k为平移因子，决定尺度函数在x轴上的位置(j,k∈N)。Vj为由j阶尺度函数ϕj,k张成的尺度度量空间，Vj-1是ϕj-1,k张成的空间，是Vj的子集，Vj-1的正交补集Wj-1由小波函数ψj-1,k张成，则任意一个表示在Vj上的信号F(x)都可以由Vj-1和Wj-1的两个空间中的函数基来表示，即

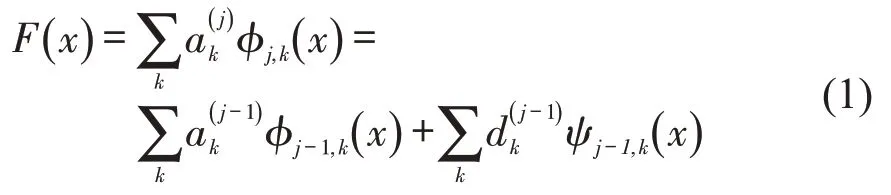
式中：ak(j-1)为尺度函数系数；dk(j-1)为小波函数系数；对应j阶信号中的低频部分；则对应高频部分。j-1 阶的低频部分可以继续按照式(1)进行分解，尺度函数每减少1阶，其中心频率就会降低，滤出的高频部分的频率也会随之降低。

(2)方向盘信号的分解

定义方向盘转角的空间域信号θ(x)，自变量x为沿道路中线方向的桩号坐标。采用Daubechies 6阶小波对θ(x)进行逐层分解，分解流程如图1所示。

图1中，an代表各级分解中的低频部分，dn代表各级分解中的高频部分，n∈N。分解结果如图2所示，第3层低频部分的重构信号去掉了原始信号的系统噪声，如图2(b)所示，实现了信号的平滑；第6层低频重构信号与路线曲率变化曲线的形态基本一致，如图2(c)所示。因此，可将第6层分解的低频重构信号作为方向盘转角的低频分量l(x)。因为Vj与Wj均为线性空间，故Wj的各子集上表示的信号是线性可加的，故d4～d6重构信号的线性叠加即是方向盘转角信号的高频分量h(x)，如图2(d)所示。

图1 小波分解流程Fig.1 Wavelet decomposition process

3 实验结果分析

3.1 自然转向行程的影响因素分析

自然转向行程是指驾驶员将方向盘从原平衡位置转动到使车辆转弯半径与圆曲线半径一致的过程中车辆行驶的里程，如图2(c)所示。根据第6层低频信号的函数图线，提取驾驶员的转向起点和转向终点，并计算自然转向行程。图3为入弯时自然转向行程随回旋线长度的变化情况，纵坐标Z为自然转向行程Ln与回旋线长度的比值，横坐标C=A/R。

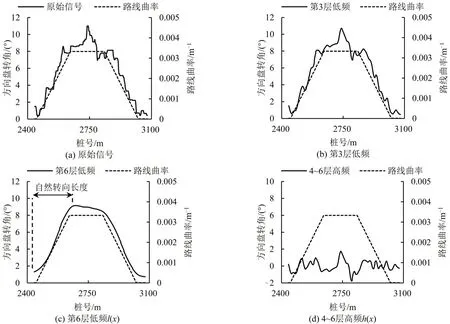
图2 方向盘转角信号的小波分解Fig.2 Wavelet decomposition of steering wheel angle signal

图3结果表明，半径为100 m，C小于1.0时，超过1/2的驾驶员自然转向行程大于实际的回旋线长度。与之相似的，当半径为200，300，400，500 m，1/2驾驶员的自然转向行程大于回旋线长度时对应的C的临界值分别为0.9、0.8、0.7和0.6。为进一步探究Ln的影响因素，以Ln为因变量，R、C为自变量进行多元回归分析，同时验证转向D的影响(D为分类变量，左转取0，右转取1)，回归的结果如表2所示。

表2结果表明，入弯时自然转向行程Ln与半径、回旋线长度均显著相关，在半径一定的条件下，自然转向行程会随回旋线长度的增加而减小。而弯道转向对自然转向行程影响不显著。

3.2 驾驶员入弯时的曲率感知特性分析

在入弯时，路线半径的变化率ΔR逐渐下降，当ΔR下降到驾驶员难以感知的程度时，他们会在缓圆点前完成自然转向。由图3结论可知，当C大于临界值时，超过1/2 的驾驶员自然转向终点位于缓圆点前。此处定义C等于临界值时，位于缓圆点前的转向终点对应的ΔR为临界半径变化率ΔRc，ΔRc的均值如表3所示，可以初步判定ΔRc与R呈负相关。

为进一步研究ΔRc与R的关系，以ΔRc为因变量，R为自变量进行一元线性回归，回归系数及检验结果如表4所示。结果表明，半径每减小100 m，1/2驾驶员对半径变化率的感知阈值就上升0.6 m·m-1。当ΔR大于ΔRc时，越来越多的驾驶员对路线曲率的变化不敏感。说明曲线半径越小，驾驶员对半径变化率的敏感程度越高，这与Hasan[13]的结论是相似的。

3.3 轨迹修正行为分析

(1)方向盘的平均摆动幅度

高频分量h(x) 是驾驶员在弯道中用于轨迹修正的操作序列。假设车辆横向位置的期望为一定值，那么高频分量在空间域上是期望为0的随机信号。该信号的平均功率p反映了驾驶员在修正轨迹过程中方向盘摆动的平均幅度，p等于信号的功率谱密度函数在空间频域上的积分，功率谱密度函数与自相关函数是一个傅里叶变换对，即

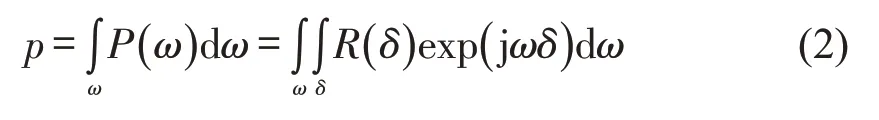
式中：P(ω)为信号的功率谱密度函数；ω为信号的空间频率；R(δ)为信号的自相关函数；j 为虚数单位；δ为空间延迟距离。p的平均值随C的变化如图4所示。

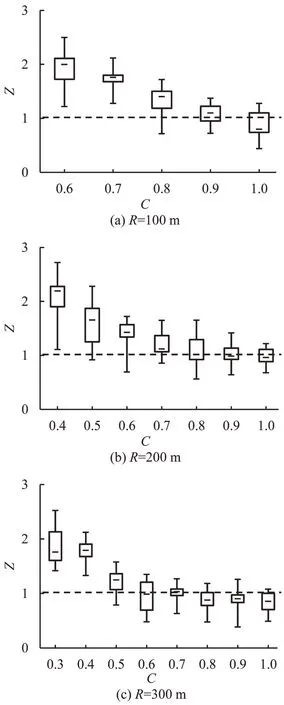
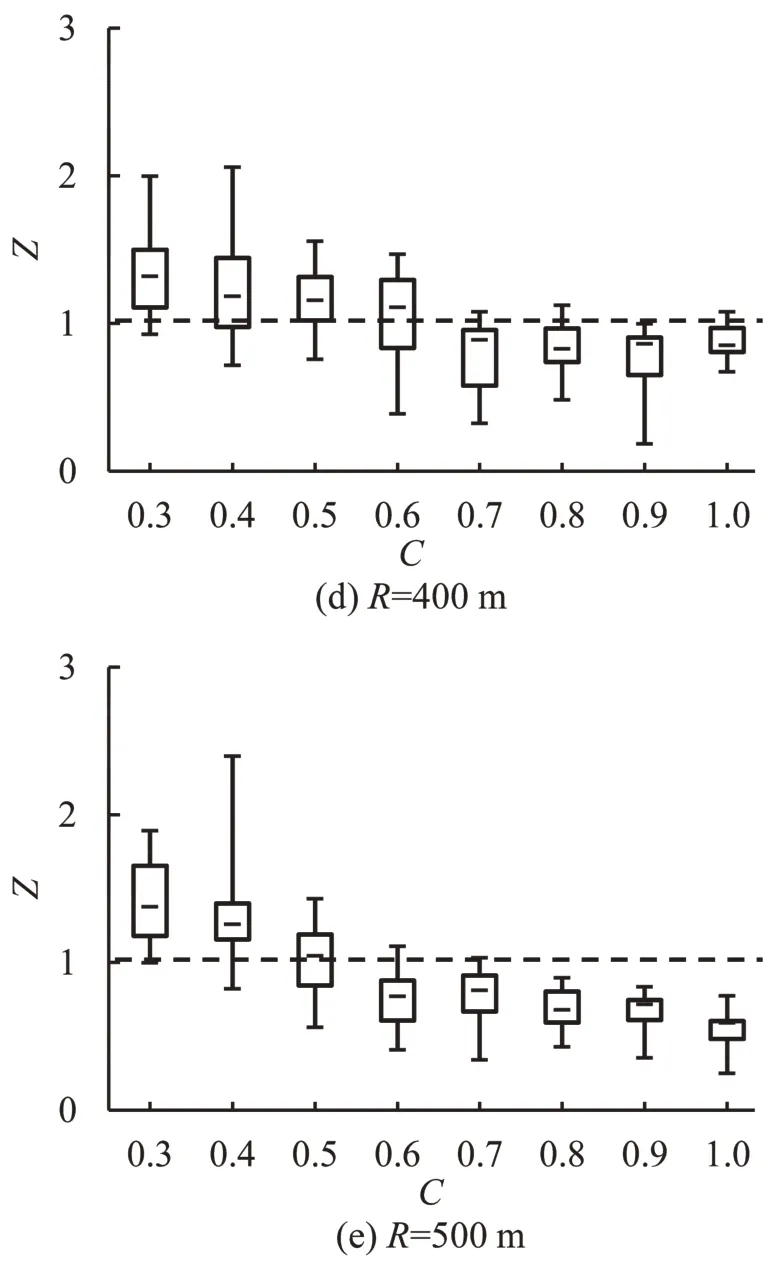
图3 回旋线长度与自然转向行程的比例Fig.3 Ratio of spiral length to natural turning path

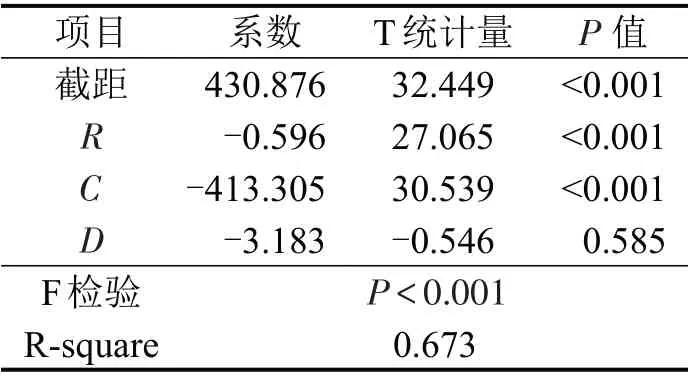
表2 Ln 的回归模型Table 2 Regression model of Ln

表3 临界条件下的自然转向终点曲率变化率Table 3 Curvature change rate of natural turning end point under critical condition

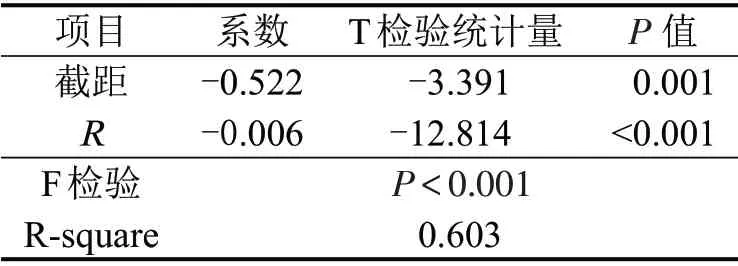
表4 ΔRc 的回归模型Table 4 Regression model of ΔRc

图4结果表明，随着C的增加，轨迹修正操作中方向盘的平均摆幅整体呈波动下降的趋势，说明回旋线曲率变化越平缓，修正操作的负荷越低。半径为200 m 的曲线组，p在C大于0.6 后趋于稳定。半径300，400，500 m 的曲线组，p在C大于0.5后趋于稳定。出弯时方向盘的平均摆幅整体高于入弯。对比不同半径条件下的结果可知，半径越大，方向盘的整体摆幅就越低，车辆轨迹的整体稳定性也就越高。

(2)方向修正回转速率

驾驶员在紧急回转修正时会让车辆受到一个附加侧向力作用。这种回转修正表现在4～6 层高频信号，即h(x)曲线的极值点处，这些点的曲率反映了方向盘在回转操作中转速的变化率，如图5所示。

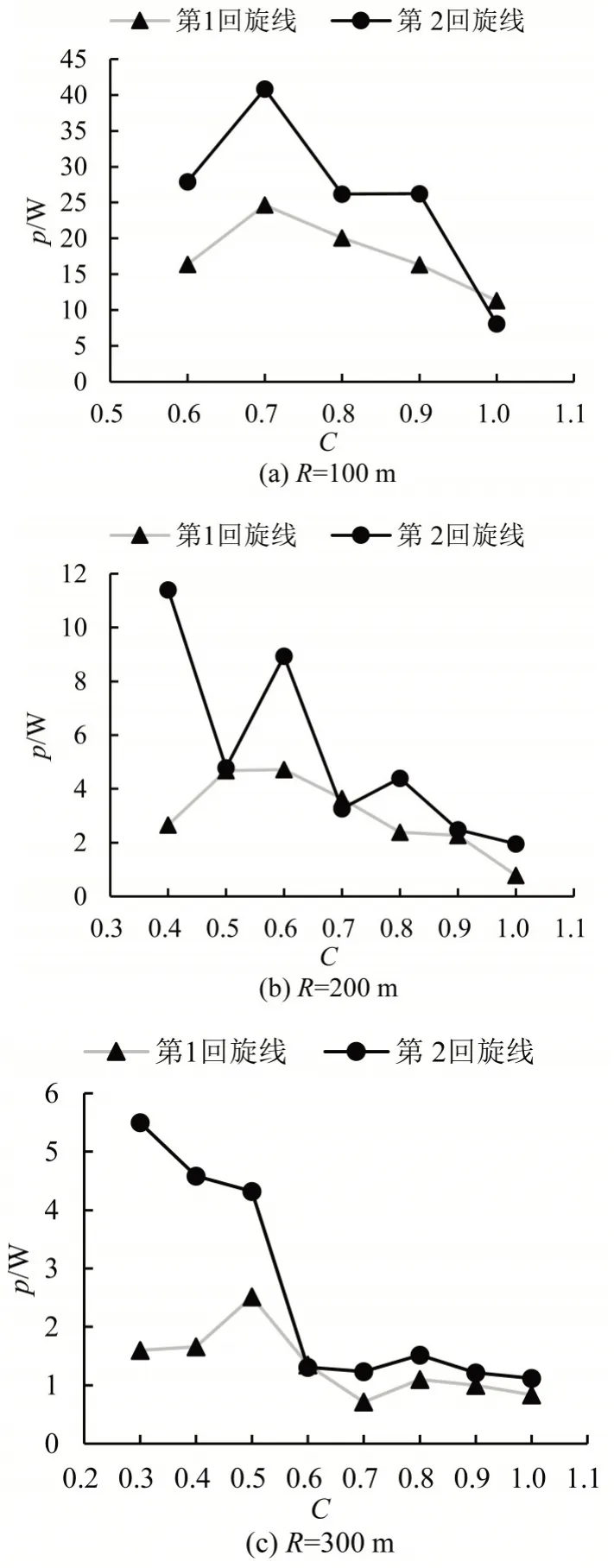
图4 h(x)的平均功率与回旋线长度的关系Fig.4 Relationship between average power of h(x)and length of spiral

图5中：α为信号曲线上极值点附近M处的切线与横坐标轴正方向的夹角；Δα为点M处切线和点M′处切线间的夹角；Δs为点M和点M′之间的弧长。当回转方向与路线转向相同时，车辆行驶轨迹的曲率会逐渐增大，如果此时转速过快，则侧向加速度会有一个较大的瞬时增量，不利于车辆侧向稳定。

图5 高频分量的极值点曲率Fig.5 Curvature of extreme point of high frequency component

图6反映了h(x)极值点曲率最大值随C的变化情况，总体上看，最大曲率随回旋线长度的增加而呈现波动上升的趋势，说明回旋线越长，就越容易在某个瞬间出现方向盘转速过快的现象。入弯时的曲率最大值低于出弯，说明入弯时驾驶员的操作相对平稳。对比不同半径的结果可知，随着半径增加，曲率最大值整体降低。说明半径越大，方向盘的回转速率越低。

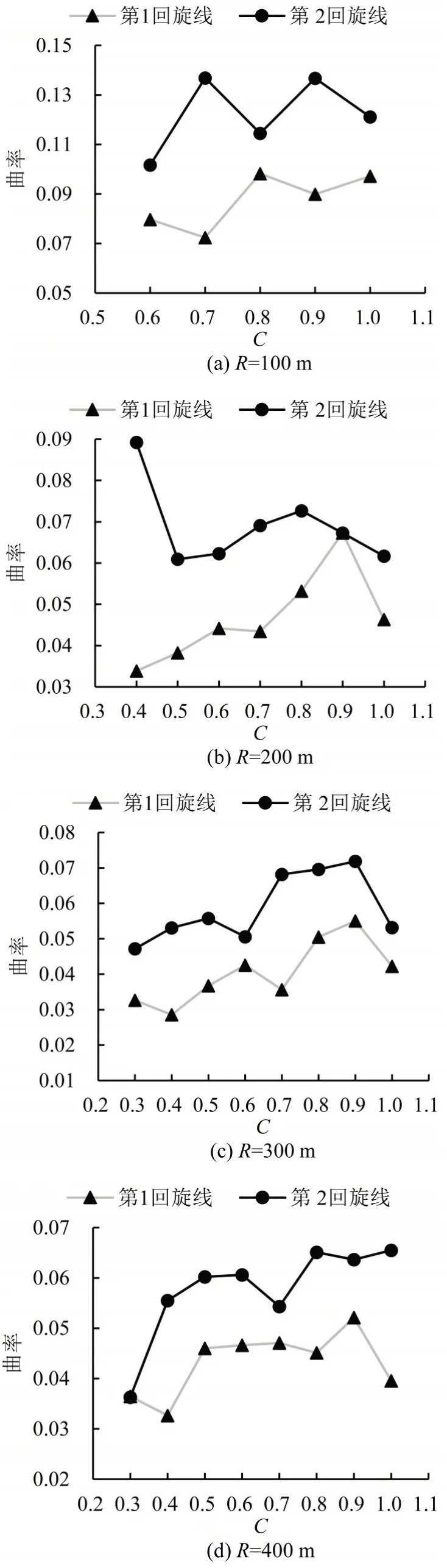
图6 h(x)极值点曲率与回旋线长度的关系Fig.6 Relationship between curvature of extreme point of h(x)and length of cyclotron

4 结论

本文运用驾驶模拟实验分析了驾驶员在双车道公路回旋线路段的转向行为，揭示了半径与回旋线长度对自然转向和轨迹修正行为的影响，结果表明：入弯时驾驶员对回旋线曲率变化的敏感度随圆曲线半径的增大而减小，自然转向行程与半径、回旋线长度均相关。从轨迹修正行为的分析结果可知，较长的回旋线虽然可以降低轨迹修正时方向盘的摆动幅度，但会增大回转速率，不利于车辆的横向稳定。

综合自然转向及轨迹修正行为的分析结果，当回旋线长度接近驾驶员的自然转向行程时，用于轨迹修正的方向盘摆动幅度和瞬时回转速率均处于较低水平。因此，以自然转向行程作为回旋线的理想长度是合理的。经计算，理想回旋线长度Ls,i的建议取值为：R=100 m时，Ls,i宜接近100 m；R=200 m时，Ls,i取98～128 m；R=300 m时，Ls,i取108～147 m；R=400 m时，Ls,i取100～144 m；R=500 m时，Ls,i取125～180 m。该建议值适用于设计车速40～60 km·h-1的双车道公路。