中小尺寸截面薄壁顶管顶推力的估算

杨 凯，肖尊群*，2，刘胜兵

1. 武汉工程大学土木工程与建筑学院，湖北 武汉 430074；2. 武汉工程大学兴发矿业学院，湖北 武汉 430074

大型管幕群的单根顶管的施工通常采用泥水平衡顶管技术。顶推力是顶管工程的一个重要施工参数。顶推力通常由端头迎面阻力和管壁侧摩阻力构成。关于顶推力的估算公式，国内外已经有不少研究成果。日本污水协会［1］提出JMTA 公式。Shimada 等［2］也提出了顶推力的经验估算公式，张鹏等［3］基于Persson 模型进一步得出考虑管土接触属性的顶进力估算公式。Chapman 等［4］和Sterling［5］基于现场监测数据，提出了考虑管土作用机理的顶推力预测模型。Beckmann 等［6］基于CoJack 法计算极限分析理论得到顶管最大允许顶推力估算公式。这些经验公式都是针对单个顶管，未考虑相邻既有顶管对顶推力的影响。同时，这些公式都是把单个管节假定为刚体进行推导，未考虑顶进过程中顶管本身的变化对顶推力的影响。一般而言，管幕群由多个薄壁顶管组成，按照一定的顺序开展顶管施工，相邻既有顶管对顶管顶推力有影响，甚至是不可忽略的。

为了研究相邻顶管对顶管顶推力的影响，采用强制位移法建立顶管顶进过程的数值分析模型，分析既有顶管存在的位置对顶管顶进力的影响。数值方法在确定顶管外壁与周围土体的接触力学行为方面较其他理论方法更具优势。Barla等［7］利用PFC2D 提高了微隧道技术在都灵地区的适用性，提出了微隧道顶推力的估算方法。Hasanpour 等［8］模拟了盾构掘进过程，以防止挤压场地中由于较大的位移导致岩体渗透到盾构单元中。王贺敏等［9］通过建立矩形顶管工程施工的有限元分析模型，研究顶管顶进过程中顶管施工影响范围内典型纵断面和横断面的地表沉降变化规律。Ji 等［10］通过对沈阳市沙质土的微参数进行校准，利用颗粒模型再现沙质土的宏观材料行为，推导出绕管周的法向力。柳军修等［11］基于大口径深埋顶管长距离穿越无水砂层现场试验，采用FLAC3D 建立三维精细化数值模型，分析顶管顶进及管节与周围砂层相互作用。Yen 等［12］通过建立有限单元模型并提出位移控制法，得到钢筋混凝土厚壁圆形顶管顶进力与顶进距离的拟合公式。赖金星等［13］以某污水顶管工程为背景，构建三维弹塑性有限元计算模型的方法，分别考虑正面推进力等对土体变形的影响。张文瀚等［14］结合西气东输二线南昌到上海支干线7 标段杭州市高速公路顶管穿越工程，通过模拟顶管施工中机头支护压力和注浆压力等变异情况的分析，对路基变形影响的变化规律。黄章君等［15］为分析顶推反力荷载对墙后土体位移、应力、孔隙水压力等的影响，建立顶管顶进过程中工作井反力墙稳定性的动态三维有限元分析模型。以上都是数值模拟计算的先例，说明该方法估算顶推力是合适的。而且对于小截面尺寸的细长薄壁顶管，该方法自动考虑顶管本身的变形对顶推力影响，估算优势更加明显。

本文以港珠澳大桥的拱北隧道管幕工程为研究背景，选取中等埋深位置的顶管作为研究对象，将既有顶管设置在不同位置，然后对顶管顶进过程进行数值模拟，得到不同工况下顶进力随顶进距离的拟合函数，分析相邻既有顶管对顶进力的影响。

1 数值仿真模型

1.1 工程背景

根据文献［3，16］，港珠澳大桥的拱北隧道暗挖段长255 m，断面面积338 m2，是世界上开挖断面最大的单个隧道。拱北隧道采用管幕暗挖法施工，管幕工程由36根直经为1 620 mm、长度为255 m、曲率半径886～906 m 的曲线钢管组成。每根顶管由64 个管节组成，管节长4 m，重4.3 t，顶管间距35.5～35.8 cm，最小埋深5.8 m，最大埋深29.8 m。顶管编号与顶进顺序编号如图1 所示。隧道穿越地层多为软弱地层，上覆敏感建筑和管线等构筑物，施工条件复杂。土层物理力学参数的选择应综合考虑珠海市境内及附近工程地质勘查的结果和相关工程经验，土层的物理参数如表1 所示，地下水位在地表以下1 m。

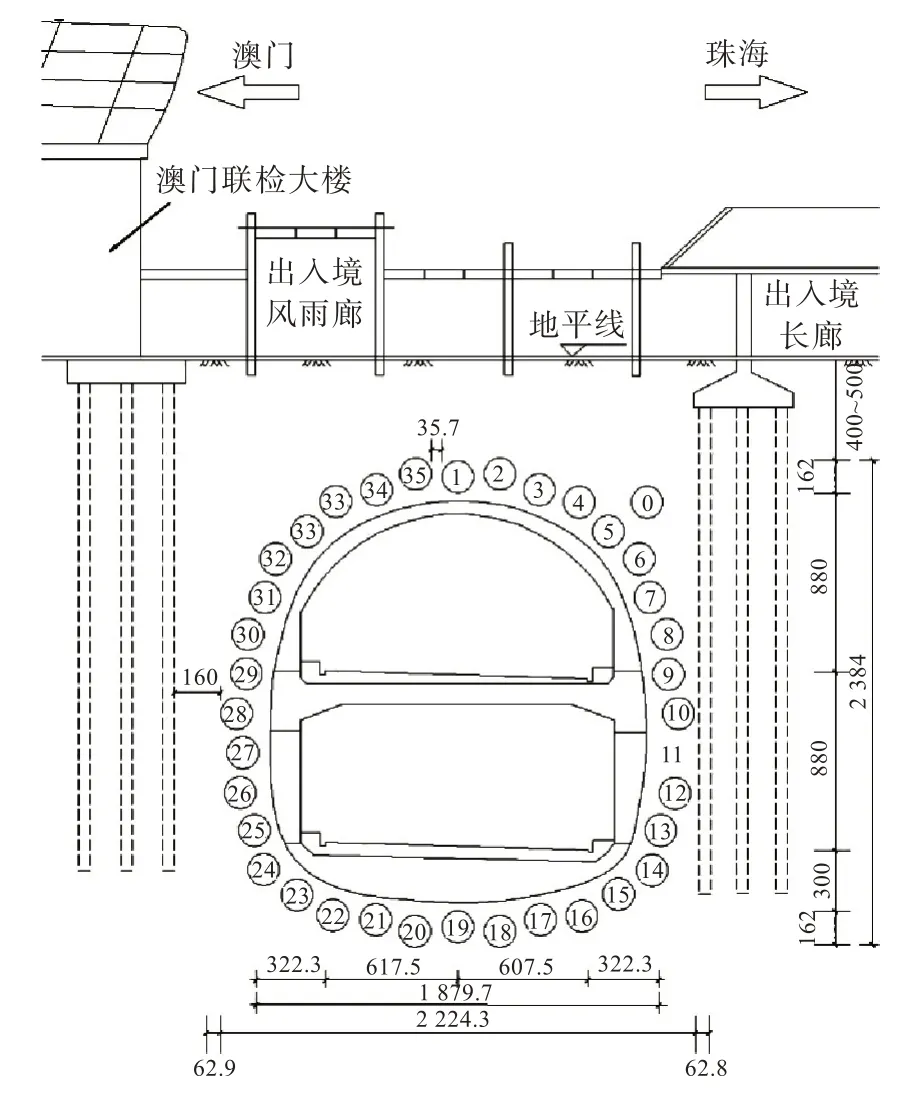
图1 隧道断面图［3，16］（单位：mm）Fig.1 Tunnel section（unit：mm）

选取5#、9#和17#顶管，建立顶管顶进过程的数值模拟模型组，通过与实测顶推力-距离拟合曲线对比，论证模型估算顶推力的合理性，然后改变临近既有顶管的安装位置，分析临近既有顶管的安装位置对顶管顶推力的影响。

1.2 数值模型设置

1.2.1 几何模型 以9#顶管为例建立数值模型，其他顶管与9#顶管类似。模型的宽度和高度均为40 m，长度为255 m。顶管及其侧壁土体部分网格划分加密，其他位置网格相对稀疏。另外在不同顶进位置设置1 个管节的顶进距离（4 m），顶进位置的网格应均匀设置，以便计算得到顶进力与顶进距离的拟合曲线（图2）。9#顶管的顶进位置分别设置在距离始发井8，20，48，80，120，160 m 处。9#顶管沿顶进方向分别穿越砂性土和淤泥质黏土。顶管截面尺寸与实际顶管一致，截面面积为0.102 m2。顶管顶进完成时，顶推力通过起始管节的起始单元截面结点纵向应力平均值与截面面积的乘积计算。3 组模型的单元数统计如表2 所示。

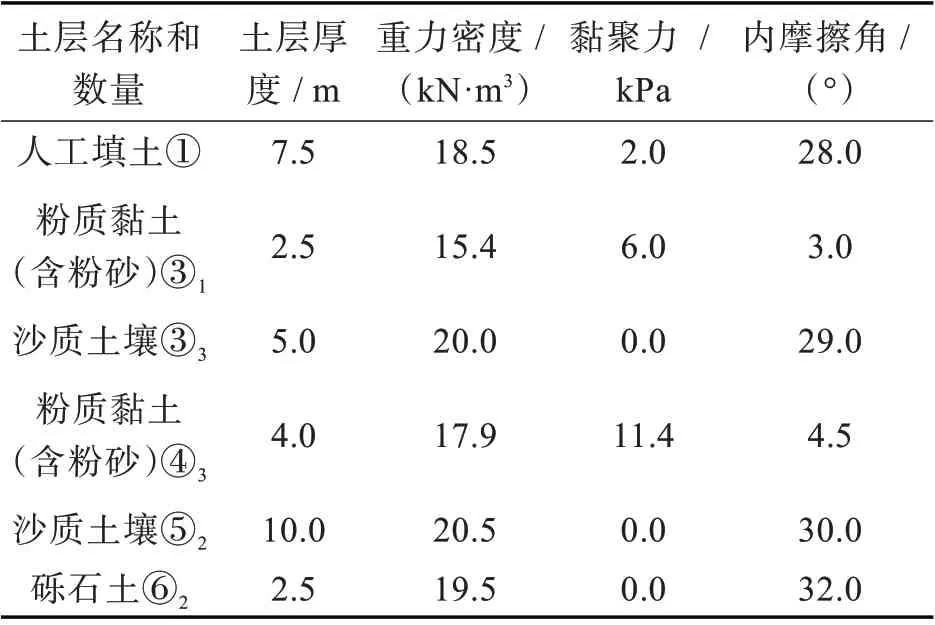
表1 土层物理力学参数［3］［16］Tab.1 Physical and mechanical parameters of soil layer

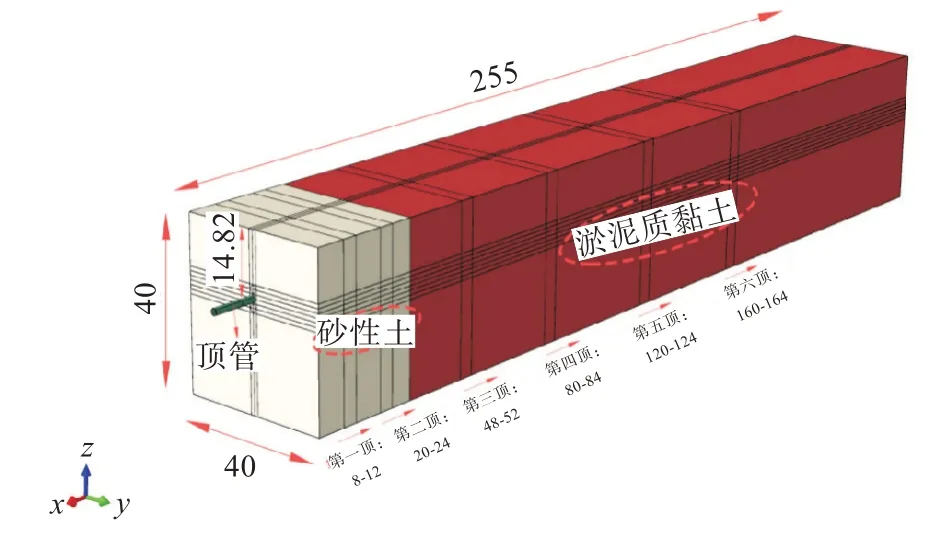
图2 整体模型尺寸与顶管（9#）顶进位置分布（单位：m）Fig.2 Overall model size and jacking position distribution of 9#pipe jacking（unit：m）

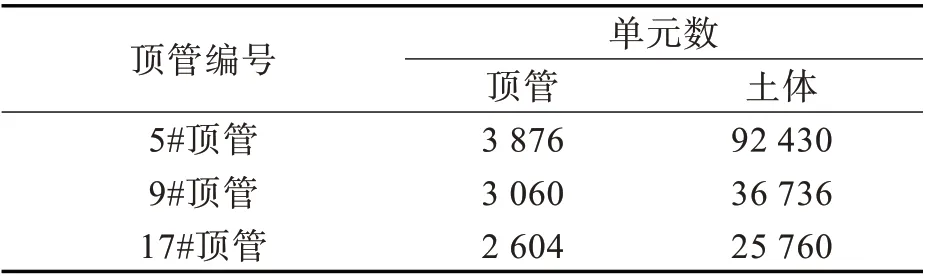
表2 三组模型的顶管和土体的单元数Tab.2 Pipe jacking and soil element number in three groups of models

1.2.2 相邻顶管位置设置 5#、9#顶管相邻顶管顶进位置设置如图3 所示，设置工况分为4 种，分别为上下无临近顶管、下方有临近顶管、上方有临近顶管、上下有临近顶管。17#顶管相邻顶管顶进位置设置如图4 所示，设置工况也分为4 种，分别为左右无临近顶管、左边有临近顶管、右边有临近顶管和左右有临近顶管。

1.2.3 物理力学参数 顶管管片为钢管，模型选用线弹性模型，材料物理力学参数如表3 所示。顶管机机头内部由各部件组合而成，实际质量比钢材要轻很多，因此，在模型中，实心机头的密度为钢材密度的1/3 较为合理。

图3 5#和9#顶管相邻顶管位置设置：（a）上下无临近顶管，（b）下方有临近顶管，（c）上方有临近顶管，（d）上下有临近顶管Fig.3 Positions setting of adjacent pipe jacking from 5#and 9#jacking pipes：（a）without adjacent pipe jacking on top and bottom，（b）with adjacent pipe jacking on bottom，（c）with adjacent pipe jacking on top，（d）with adjacent pipe jacking on top and bottom

图4 17#顶管相邻顶管位置设置：（a）左右无临近顶管，（b）左边有临近顶管，（c）右边有临近顶管，（d）左右有临近顶管Fig.4 Positions setting of adjacent pipe jacking from 17#jacking pipe：（a）without adjacent pipe jacking on left and right，（b）with adjacent pipe jacking on left，（c）with adjacent pipe jacking on right，（d）with adjacent pipe jacking on left and right

管幕工程涉及的深度和跨度大，土体类型分布沿竖直和水平方向分布复杂，若按照实际土体材料类型建模，很难实现地应力平衡。整个模型简化为两种土体材料。材料参数根据实测参数进行竖向和水平向的加权平均。经过初步敏感性分析，发现土体本构对顶推力的影响较小，因此，建模时，所有土体材料本构模型均选择考虑流动关联准则的D-P（Drucker-Prager）模型。

经过简化处理模型的土体材料物理力学参数如表4 所示。

表3 顶管的物理力学参数Tab.3 Physical and mechanical parameters of pipe jacking

表4 模型土体参数（D-P 模型）Tab.4 Soil parameters of model（D-P model）

1.2.4 接触属性 通过位移控制建立的数值模拟模型直接计算得出的顶推力，并不是很精确。因为在实际施工过程中，现场主要根据顶管的施工情况向顶管与土体之间添加润滑泥浆进行减阻，所以顶管与土体之间并未完全接触。因此本文在建立顶管与土体的接触范围时将其分为顶管-土体接触和顶管-泥浆接触两个部分考虑。另外管-土接触范围的接触特性通过综合考虑穿越土性、润滑浆液减阻、顶管外壁涂蜡等减阻措施并结合现场实测确定管土的摩擦系数。

顶管机头刀盘转动有助于减少土壤和管道之间的接触面积和摩擦。通过改变管道与土壤之间的接触范围，可以模拟超切和泥浆套。通过试算，1/4 接触模型计算得到的顶推力与实测顶推力拟合度最高，本模型均选用1/4 接触。管土接触的摩擦系数通过实测获得，在0.002～0.023 之间取值［3，16］，具体参数通过试算获得。

2 结果与讨论

实测顶推力、JMTA 公式和数值模型计算得出的顶推力与顶进距离的拟合曲线如图5 所示。JMTA 公式计算得到的顶进力远远大于实测顶进力，无讨论意义。因此，本文只讨论不同相邻顶管对顶管顶进力的影响。

图5 顶管的实测顶推力与计算结果对比：（a）5#，（b）9#，（c）17#Fig.5 Comparison of jacking force between field data and calculation results of pipe jacking：（a）5#，（b）9#，（c）17#

由图5（a）和图5（b）可以看出：5#和9#顶管，数值模拟得到的顶进力拟合曲线与实际监测数据大致相同，其中上下存在临近管的4 种工况中，上下有临近顶管的情况下，所得的顶推力变化不大，且顶管下方有临近顶管更加接近实测数据；当顶管顶进距离在175～225 m 时，数值模拟计算得到的顶进力略大于实测顶进力。数值仿真得到的不同顶进方案下所得的顶推力与顶进距离的拟合关系基本呈线性分布趋势，而实际顶进过程中顶推力与顶进距离的关系基本呈非线性趋势，中间段非线性更明显。

由图5（c）可以看出：17#顶管，当顶管顶进距离在20～100 m 时，数值模拟与实际监测数据大致相同，且顶管左边有临近顶管和右边有临近顶管时顶推力与顶进距离的斜率出现突增；当顶管顶进距离在100～225 m 时，数值模拟都大于实际监测数据，且顶管左右无临近顶管和左边有临近顶管对顶进力的影响非常明显。数值模拟中顶管左右无临近顶管和左右有临近顶管所得的顶推力与顶进距离的关系基本呈线性分布趋势，而实际顶进过程中顶推力与顶进距离的关系相比5#和9#顶管而言，呈非线性趋势更加明显。

3 结 论

1）在顶管在顶进过程中，对于顶管上下存在临近管的4 种工况而言：如果顶管上下存在临近管时，优先施工该顶管下方的顶管，然后施工该顶管；对于顶管左右存在临近管的4 种工况而言：若顶管左右存在临近管时，优先施工该顶管，然后施工其他顶管。该施工顺序可以有效地降低临近顶管的顶推力的影响，从而得到相对较低的顶推力，减少顶进过程对土体的扰动。

2）数值方法所得的顶推力与距离的拟合曲线表明：顶管在0～100 m 过程顶进时，数值模拟得出的顶推力小于实测顶推力；顶管在100～255 m 过程顶进时，数值模拟得出的顶推力大于实测顶推力。

3）JMTA 理论公式与数值模拟计算得出的顶推力与实际监测的顶推力相比，数值模拟的结果更加接近实测数据。