改进SPTA 在ARM 平台上的应用与分析

刘 帅，冉 全，宇文涛

武汉工程大学计算机科学与工程学院，湖北 武汉 430205

为了适应市场需要，电解质分析仪等对步进电机需求量大的设备，在增加功能的同时需要提高定时器资源利用率来满足对步进电机的控制。因此，提高原有芯片上的定时器资源利用率成为亟待解决的问题。步进电机作为一种常用的执行机构，它可以通过输入脉冲信号控制，定位精度高、控制可靠、定位保持力强、以及可实现开环控制［1］。因此，步进电机在智能控制系统中的多轴控制领域中具有广泛的应用［2-3］。

传统的步进电机控制算法有梯形算法和S 形算法。常见的S 形算法有：7 段式S 形算法、5 段式S 形算法［4-5］。在传统控制中这类算法每个定时器只能控制一个步进电机，当资源紧缺的时候往往需要扩展芯片来协同处理，占用芯片资源较多。而时间片步数算法（steps-per-time-algorithm，SPTA）是在定时器中断内计算步进电机运动步数，当中断时间能够满足计算多个脉冲参数时，能在各自条件成立时改变芯片引脚输出状态达到输出多个步进电机脉冲的目的。这样在一个定时器内就可以发出多个脉冲信号，从而对多台步进电机进行控制。

本文探讨了梯形算法、S 形算法、普通SPTA 算法与改进SPTA 算法在精简指令集的芯片（advanced RISC machine，ARM）平台上的实现方法，实验结果表明，在频率段区间内改进SPTA 算法在定时器资源利用率及控制效率等综合性能上优于其他控制算法。

1 相关工作

梯形算法主要优点在于算法简单易实现，梯形算法在STM32 平台上运行时拥有较快的响应速度，可以实现步进电机的平稳运行［6-7］。但由于速度变化时曲线不够平滑，会导致电机产生柔性冲击，因此梯形加减速算法应用在对加减速变化要求不高的场合。

为解决梯形算法的缺点，通过指数函数构造加减速运动模型提出7 段S 形算法，该算法相比于梯形算法，由于运动过程中速度变化平缓，在相同工作场合中S 形算法控制下的步进电机基本无冲击导致丢步的现象［8］。但该算法在提高精度的同时增加了算法的复杂性，影响电机响应时间。5段S 形算法由7 段S 形算法之上演变而来，5 段S 形算法使得程序更加轻量化，较好地降低了存储资源的占用［9-12］。因此这类S 形算法被广泛应用于对精度要求高的场合。这类算法都是通过改变定时器预分频值来改变电机脉冲频率，实现步进电机的精确控制。但是传统的控制算法往往一个步进电机就需要单独的一个定时器来控制。

在定时器资源占用这个问题上，一种新的控制算法被提出，SPTA 算法是将运动时间分割成若干个合适的小时间片。在每个时间片内它都将速度参数加到位置参数上，如果位置参数溢出，它就会输出一个脉冲。速度参数溢出频率越高，电机运行的频率也就越高［13］。该方法很大程度地节省了芯片资源，SPTA 算法采用4 个状态转换来控制步进电机运动。

ARM Corte-M4 处理器在M3 的基础上强化了运算能力，新加了浮点、DSP、并行计算等，其高效的信号处理功能与Cortex-M4 系列处理器的低功耗、低成本和易于使用的优点的组合［14-15］。该处理器在电动机控制、嵌入式系统以及工业自动化市场有着广泛的应用。本文基于ARM Cortex-M4平台上实现了改进SPTA 算法与上述梯形算法、S形算法、SPTA 算法的对比实验。

2 改进算法控制方案

改进SPTA 控制算法是通过对7 段式S 形算法做改进，去掉匀加速、匀减速阶段，引入了Sigmiod函数曲线作为速度变化曲线。因此，改进SPTA 算法的应用，一方面减少如梯形算法中频率突变带来柔性冲击；另一方面也减少了7 段式S 形算法的处理时间，提高了算法运行效率。控制状态如图1所示。

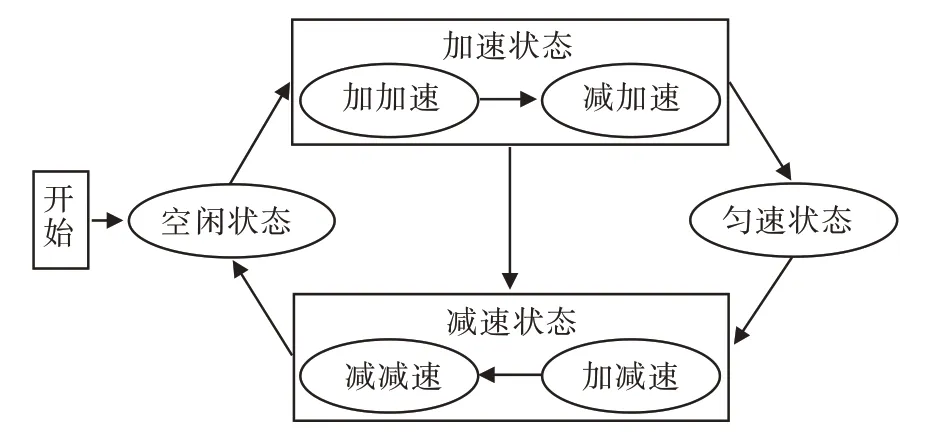
图1 改进SPTA 的状态切换图Fig.1 State transition diagram of improved SPTA

S 形曲线模型是在原Sigmoid 函数上转换为分段函数，各段对应其加减速控制过程，t0～t2段对应加加速阶段和减加速阶段；t2～t3段对应匀速阶段；t3～t5段对应加减速阶段和减减速阶段。对应ν - t曲线转换成通用表达式为：

式中νmin为电机起始速度，νmax为电机最大速度，b的值控制速度曲线在速度轴方向拉伸，且b 值与频率差值正相关，关系为b = νmax- νmin；a 的值控制函数曲线在时间轴方向的拉伸，各运动状态时间段参数满足以下关系：

设置的加减速时间过长会导致启停速度变化慢，在实际应用上需要将公式（1）中b = νmax- νmin对应调整为b = k1νmax- k2νmin，便于减少启动以及停止时间。通过设置参数a 的值满足当t = t2时ν →νmax。结合 公式1 将ν - t 函 数转换为f - t 函数表达式为：

改进SPTA 算法思想为：电机控制任务运行后根据提供的各项参数和算法处理时间设置最大定时器中断时间。频率调整后，根据相应参数调整若干次中断发一脉冲，并在中断里计算当前频率段脉冲个数。脉冲数发完后重新对相应频率段内脉冲数计数，直到设定的总步数运动完成。

3 实验平台搭建

控制系统的主控芯片采用ARM Cortex-M4 内核的STM32F4 系列32 位微控制器，能够在复杂的控制场合很好的满足应用。上位机通过串口与硬件平台通信实现数据通信，下位机通过TB6560AHQ 步进电机驱动器实现电机的控制，硬件平台系统框图如图2（a）所示。

图2 （a）系统框图，（b）程序流程图Fig.2 （a）System diagram，（b）program flowchart

软件系统开发环境选用keil-MDK，该开发环境也是现在主流的开发环境之一，环境稳定、调试便捷。通过调试功能测试算法运行时间，配置一个常开的定时器，定时器最大频率能保证算法正常运行完成。设置计算加减速频率段来选择发一个脉冲所需的中断数，核心的函数和变量如表1所示。

表1 核心变量/函数表Tab.1 Core variable/function

变量interruptCount 用来计算最大中断频率下发一个脉冲所需要进中断数量。ParameterHandle（）函数用来获取上位机传入的控制参数：电机编号、运动方向、最大频率、最小频率、台阶数、总步数、加速时间，并通过这些参数计算出各频率段频率值。函数PulseCountAlgorithm（）为中断内处理函数，用于计算当前电机各频率段运动步数，从而实现对步进电机的加减速控制，程序流程图如图2（b）所示。

4 实 验

实验设置定时器中断频率为5 000 Hz，步进电机相关运动参数为：起始频率fmin= 500 Hz，运行最高频率fmax= 2 000 Hz，加速过程时间为t3- t0=2 s，台阶数n = 20。通过python 工具仿真频率-时间曲线，如图3（a）所示，提取改进SPTA 算法中每个频率下的脉冲数和所需时间得到离散数据如表2 所示。

图3 （a）频率变化曲线图，（b）频率变化离散图Fig.3 （a）Frequency curve，（b）frequency piecewise line

表2 改进SPTA 算法数据离散表Tab.2 Discrete data of improved SPTA

表2 记录了2 s 内加速过程的相关数据，根据加速阶段的离散数据仿真出频率变化离散曲线，如图3（b）所示，其中加速和减速分为5 个阶段，仿真的曲线与算法曲线一致。

通过软件调试，中断定时器可设置最大中断频率为7 692 Hz，取整为7 500 Hz。通过在电解质分析仪上的实验分析，仪器所需步进电机频率范围为2 000～3 000 Hz。改进SPTA 控制算法综合性能表现良好，仪器运行稳定、定位精度符合要求，如图4（a）、图4（b）所示。3 台步进电机同时工作的情况下，各算法实验数据如表3 所示。

图4 实验设备：（a）正视图，（b）采样针初始位Fig.4 Experimental equipment：（a）front view，（b）initial position of sampling needle

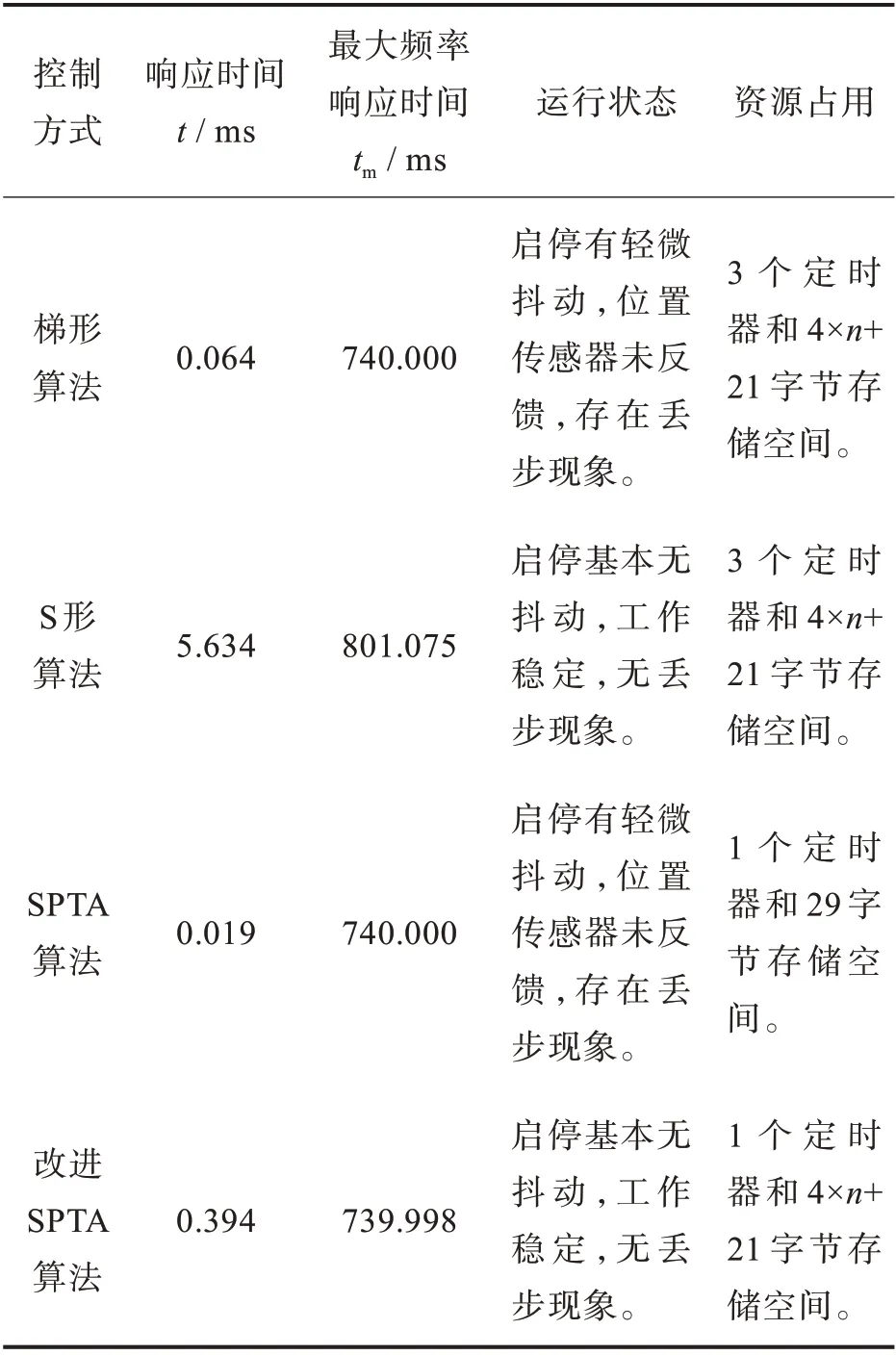
表3 实验数据表Tab.3 Experimental data

保证定位精度的前提下，通过设定不同工作频率，改进SPTA 算法与S 形算法在一个定时器资源下各频率段内控制步进电机数量的实验结果如图5 所示。

实验验证了改进SPTA 算法的可行性。在电解质分析仪上步进电机在各频率段响应迅速、运行稳定、定位准确，未出现丢步现象。由于工作频率限制，算法更适用于脉冲频率不高且要求高精度的场合。

图5 算法性能图Fig.5 Algorithm performance diagram

5 结 论

改进SPTA 算法在ARM 硬件平台上脉冲能稳定输出，实现了步进电机精确控制，并与其他传统步进电机控制方式在电解质分析仪上进行了实验对比。在2 000～3 000 Hz 频率段内改进SPTA 算法在芯片资源利用率上有明显优势，资源利用率提高1～2 倍，响应速度接近梯形加减速算法，响应时间差仅为0.33 ms，连续循环运行24 h，过程中未出现丢步现象。改进SPTA 算法适合在医疗行业中一些对运动频率要求不高，但对精度要求高的场合。改进SPTA 算法的研究主要方向是降低算法的复杂性，提高算法的执行速度的上限将决定算法的控制能力上限。

本文提供的控制算法在保证运行的稳定性外，芯片资源占用上较传统算法有明显优势，对多步进电机控制系统领域研究有参考价值。