非视域定位中光子飞行时间提取方法对比研究
任 禹,罗一涵,徐少雄,马浩统,谭 毅
非视域定位中光子飞行时间提取方法对比研究
任 禹1,2,3,罗一涵1,2*,徐少雄1,2,马浩统1,2,谭 毅1,2*
1中国科学院光束控制重点实验室,四川 成都 610209;2中国科学院光电技术研究所,四川 成都 610209;3中国科学院大学,北京 100049
非视域定位是一种通过提取光子飞行时间判断视线外物体位置的主动探测技术,是近年的前沿研究热点。为了研究均值滤波、中值滤波以及高斯滤波方法提取光子飞行时间的性能差异,首先用光度学方法优化了光子飞行模型中的能量变化模型,然后对三种滤波方法中的参数进行了优化分析,接着分析了三种提取方法对最大值判定法和概率阈值加权判定法的适应性,最后分别以设备和非视域物体的位置为变量,对三种时间提取算法得到的定位精度和稳定性进行了对比。仿真表明,中值滤波适用于较为狭窄的定位环境,并且有较高的定位精度;高斯滤波定位稳定性较好,并且滤波参数的选择范围更大。
非视域定位;光子飞行时间;滤波算法;适应性分析
1 引 言
隔墙观测因为其广阔的应用场景和应用价值一直是人们感兴趣的话题,比如在行车过程中可以提前判断转弯处是否有行人和车辆对行车路线可能产生影响,或者在搜救被困人员时不需要进入危险环境就可以确认是否存在需要施救的人员。随着光电技术的发展,条纹相机、单光子雪崩二极管、超导纳米线等高时空分辨率的光电设备相继问世,实现了光强的高灵敏度和时间分辨率探测。通过对光强时空分布信息的采集增加了可获得非视域信息的维度,使得非视域探测成为了可能。
2012年美国麻省理工学院的Velten等人首先使用短脉冲激光,通过连接非视域和视线范围内的中继表面散射间接照亮被测目标,使用条纹相机检测被目标表面散射回中继表面的光强时空分布,获得隐藏物体的三维信息[1]。为了分析上述物理过程该团队建立了激光脉冲从发射到被条纹相机探测的光子飞行模型。基于光子飞行模型对非视域目标的探测方法称为反向投影算法。根据反向投影算法的原理,由光束照射在中继面一个位置获得的数据不足以对物体的表面进行三维重建,所以需要通过振镜对中继面上的多个点进行扫描式的照射以获取多组数据。
上述反向投影方法首次实现了对非视域物体的三维重建,之后各种重建算法和反向投影优化算法相继被提出[2-6]。例如使用时间选通技术对非视域目标进行逐层探测,利用椭圆模式分解算法消除算法中多组数据之间信号的过度匹配引起的伪像,以及快速反向投影算法在重建效果基本不变的情况下将算法的运算速度提升了三个数量级。又如德国波恩大学团队提出了把实测中继面光强分布和多种计算机模拟结果相匹配,将差异最小情况时计算机模拟中的隐藏目标信息作为得到的测量结果[7]。2018年美国斯坦福大学的O’Toole等人使用了共聚焦光路对隐藏物体进行探测,他们将中继墙面光强分布表示为衰减项、表面反射率与时空项乘积在非视域空间的积分。其中时空项具有空间的三个维度以及时间维度,这恰好与闵可夫斯基空间空间坐标相对应。他们将这种已知中继面光强的时空分布推导物体(时间)空间分布的方法称为光锥变换[8]。这种重建算法运行速度快,对内存要求低。国际计算机视觉与模式识别会议2019年最佳论文介绍了一种将采集信号中的极值点与目标表面和墙面激光点之间的光程极值联系起来,这种方法称为费马流算法,具有较高的重建精度[9]。同年长春理工大学的刘笑纯使用调制光源构建了虚拟波,通过中继表面光强分布得到该虚拟波的相量场分布,然后将中继墙看作虚拟透镜对非视域环境进行成像[10]。
上述的几种方法基本都需要对中继面扫描的步骤,扫描过程精度要求高且费时。在具体的应用环境中,隐藏物体的三维细节有时不是最感兴趣的,比如我们需要知道拐角处是否有行人和车辆会对驾驶产生潜在的影响,而无需知道这个行人和车辆的具体特征。再考虑到三维重建需要很长时间来实现,非视域定位技术显得更具有应用前景。
来自英国赫瑞瓦特大学的Faccio等人在2015年提出了一种对非视域目标跟踪的方案[11-12]。他们发现在非视域环境中放置待测目标后测得的信号会在背景信号的基础上多出一个峰值,这个目标峰就是由于待测隐藏目标将光源发出的脉冲散射回探测器造成的。根据之前提出的光子飞行模型,被测目标对应信号所在时间就是经过物体表面散射并回到探测器的光子的飞行时间。经观察该团队认为这个目标信号是近似服从高斯分布的,所以他们将信号存在的区间单独分割出来并使用高斯拟合的方法来消除抖动,得到理想信号。根据之前的研究,信号中每个时刻对应的光子数可以认为是光子飞行时间概率的体现,所以在高斯拟合后可以得到一个呈高斯分布的光子飞行时间概率。最后根据光子飞行模型的几何关系可以得到目标物体存在位置的概率分布。
由之前反向投影算法对目标三维重建可以知道返回信号包含了物体的三维特征,不同的被测物体在探测器上得到的信号分布不应该是相同的。Daniele Faccio等人提出的目标信号高斯分布只是对其研究时的一种近似,这是将被测物体看作一个点物体时因为激光脉冲的高斯分布特性导致的。
可见这种高斯拟合的方法需要事先提取出目标信号存在的区间作为服从高斯分布的区间,否则拟合结果会出现严重的畸变。目标信号的非标准高斯分布也会给拟合结果带来不确定因素。因此我们结合反向投影优化算法中的滤波思想,比较高斯拟合和几种常见滤波器对光子飞行时间的提取效果,以及位置判定方式不同时对定位结果的影响及特性。
2 模型介绍
2.1 定位原理介绍
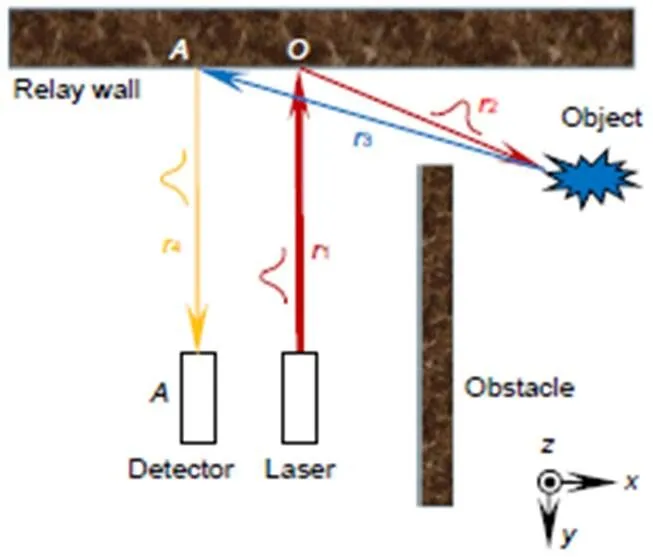
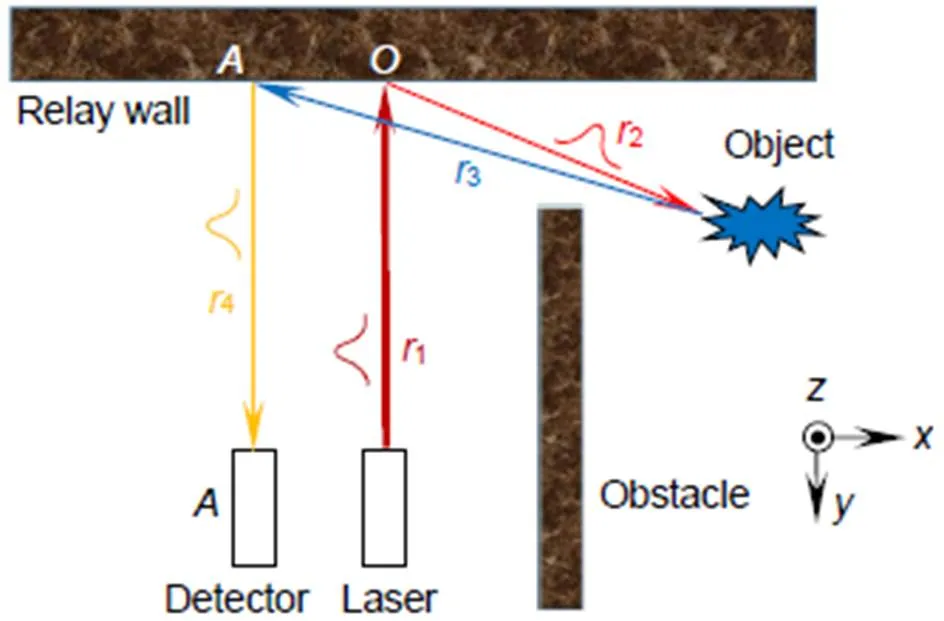
首先介绍反向投影算法的基本原理。如图1所示,从光源出射的脉冲经过光程1照射到中继墙面点,在点发生散射后一部分光经过路径2到达隐藏物体(Object),达到物体表面的光仍要发生一次散射,其中经过3散射回中继表面点的光经过光程4被条纹相机或单光子探测器等设备捕获。在这个过程中,一束激光脉冲从出发到被探测经过四段路径。探测器记录的时间就是光源发出光子经历四段光程后被探测器接收的时间,这段时间被称为光子飞行时间。根据光子飞行时间可以得到这四段光程的总和。在模型包含的四段光程中,1和4两段位于视线范围内,可以通过已有的测量方案获得。从总光程中去除1和2部分,剩余的3和4就包含了物体的三维信息。这种通过测量激光脉冲光程反解隐藏物体三维细节的方法称为反向投影算法。
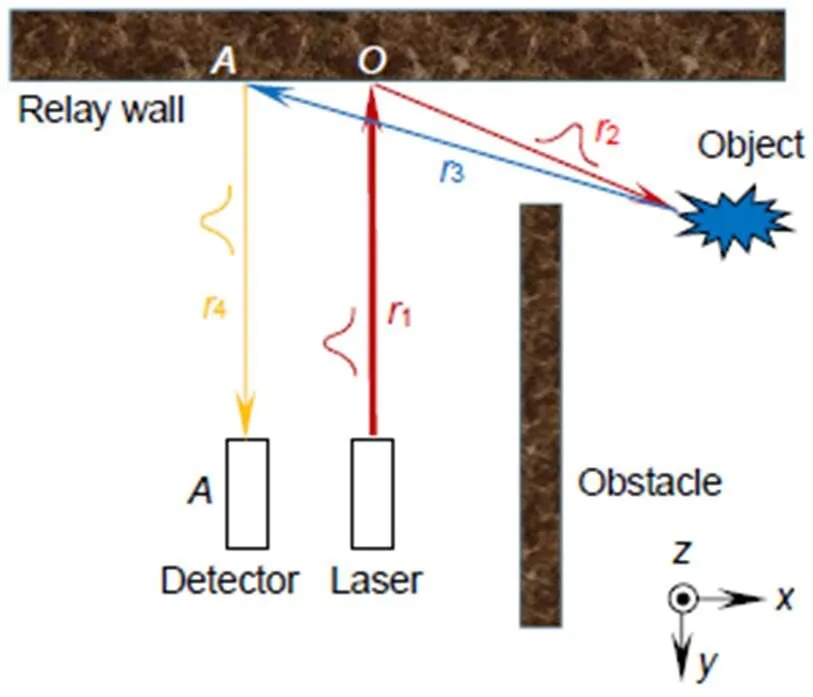
图1 反向投影算法原理
此处借鉴光子飞行模型,结合三探测通道的仿真环境对非视域定位原理进行介绍。如图2所示为三通道探测的非视域定位方案,激光脉冲从光源出射经过墙面点和物体表面的散射光分别照射到、、三点进而被相应的探测器测得。以探测器为例,根据探测器得到的光子飞行时间可以换算出飞行光程,从总光程中减去视线内的两段距离得到非视域光程对应于图2(b)中的2和3。根据一个探测器得到的光子飞行时间中两段非视域光程耦合在一起无法分离,只能判断物体存在于满足两段非视域光程和条件的位置,这些位置的轨迹根据定义形成了一个椭圆。根据每个探测器测得的光子飞行时间都可以得到一个通过物体真实位置的椭圆,显然这几个椭圆轨迹相交的位置就是非视域目标的位置。
2.2 光子飞行中的能量模型
为了模拟光源出射、传播、散射、接收等过程,利用光度学方法对该过程中能量的变化进行研究。根据之前的光子飞行模型,将光子从发射到被探测经历的过程分为两类光学现象,分别是光束的传播与散射。
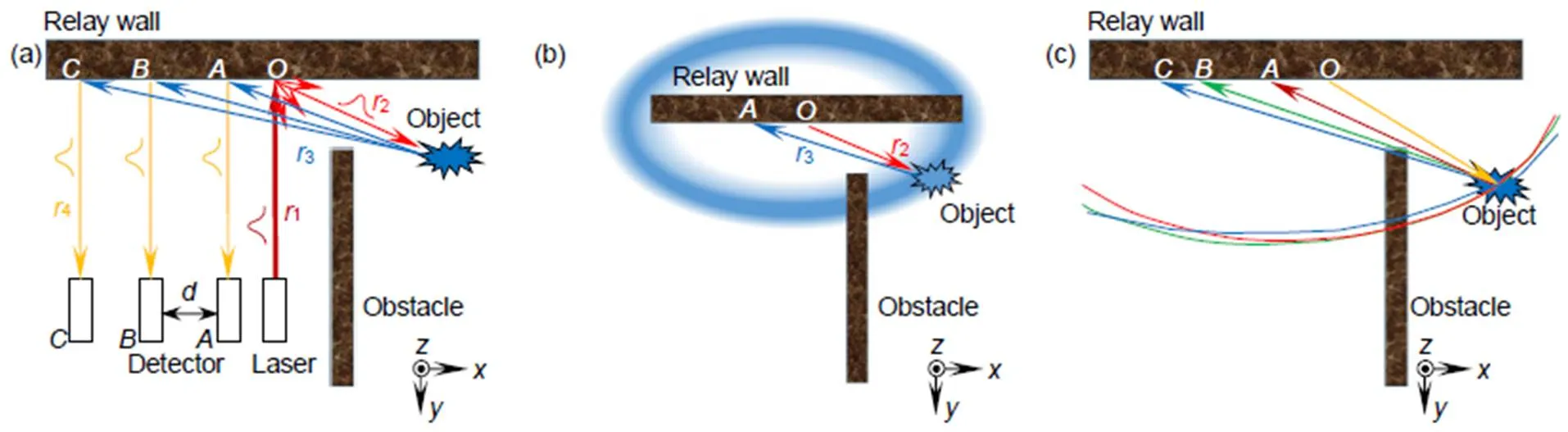
图2 非视域定位原理。(a) 定位方案;(b) 位置的椭圆概率分布;(c) 多椭圆相交定位
光源发出的激光一般经过准直后使用,所以近似认为,与光源功率相比,从光源到墙面传播过程中的发散及能量损耗是可以忽略的。然而经过中继墙面或被测物体表面散射的出射光是发散的,在这种发散光传播到下一表面的过程中,被照射面所接收的能量需要用光度学来计算。建立如图3所示的模型,从面元d1出射一束辐射亮度为的光束照射在面元d2上。d2相对于d1的位置矢量为。d1和d2法向量分别为1和2。两法向量与位矢的夹角分别为1和2。
辐照度和辐射亮度的定义分别为
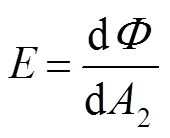

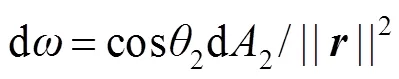
将d1面沿方向出射的辐射通量和d2面从方向接收的辐射通量作为不变量,可以得到d2表面的辐照度为

其中向量的模表示为||||。
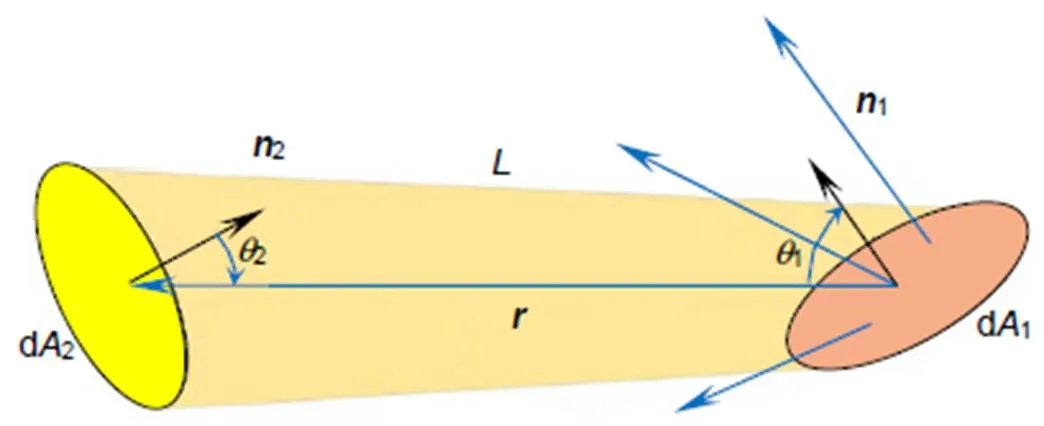
图3 光束传播中的能量变化
根据定义,双向反射分布函数为

该函数的大小由散射介质表面的光学性质和粗糙程度决定,是衡量散射过程中入射与出射光比例以及出射光空间分布的物理量。如果以日常生活环境作为非视域定位的应用环境,定位目标为非视域环境中的人,那么发生散射的墙面和衣物表面都可以近似看作均匀散射体,这种均匀散射的表面称为Lambert表面。对应于这种Lambert表面的双向反射分布函数具有不随入射和出射角度改变的性质,即为常数。为了获得更接近于真实情况的仿真,设计了双向反射分布函数的测量实验,并以普通墙面和衣物作为被测对象进行了测量。根据Lambert散射模型,墙面和衣物表面的双向反射分布函数测量结果分别为w=0.2548和c=0.1282。
为了提高模拟的真实性,不再将被测目标当作点物体[11-12],此处将被测衣物表面离散为很多微小面元,在每个面元内的参数认为是均匀的。根据光子飞行模型,以通道的探测器为例,将激光脉冲从光源出发到探测器接收的过程分为四次传播过程和三次散射过程(见图5)。四次传播过程为:从光源出发传播至中继墙面点;经点散射的出射光沿2i方向传播至衣物某表面1i;经衣物某表面1i散射的出射光沿3i传播至可以被探测器接收的墙面点;经点散射的出射光传播至探测器。三次散射过程分别发生在墙面点、被测物体表面1i和墙面点。其他探测器也遵循相同的方式测量物体散射回中继墙面的信号。
假设光源发出的脉冲功率随时间变化为0(),那么经面元1i散射回探测器的三次散射光功率是表面1i和时间的函数:

图4 散射过程中的能量变化

图5 光子飞行过程中的几何参数

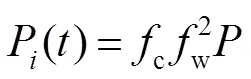
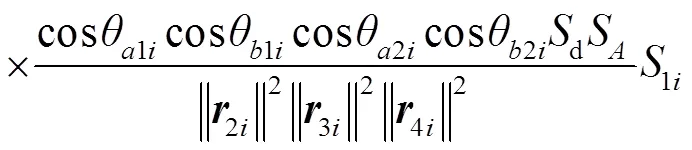
在建模过程中,我们可以将经过物体表面各点散射后传播至点的光束能量看作是简单的线性叠加,而不考虑光的波动效应。原因有以下四点:首先,考虑到单色光源被不规则的粗糙表面散射后的出射光虽然有相同的频率,但相位分布复杂,所以不具有相干性;其次,研究的尺度远远大于光源波长;参照以往的实验方案,实验中的探测器大多选用单光子探测器,是以光子的数量来体现光束能量的,并不受光束波动效应的影响;最后,即使在测量界面有波动效应引起的分布不均,其分布线度也远小于探测器线度,而且波动效应只会影响到光束能量的空间分布,对于光源脉冲周期尺度下的时间分布只会影响整体信号强度的大小而不会改变目标信号出现的时间,根据光子飞行模型确定物体信息时,光子飞行时间是唯一有效的信息。因此,探测器接收到的信号实际上是P()在1面上的积分:
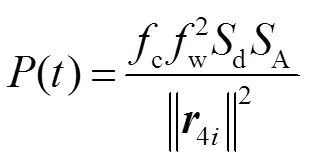
3 仿真结果
坐标系的建立参照图2(a)。激光器VisIR-1530参数:功率750 mW,重复频率80 MHz,波长1530 nm,脉冲宽度70 ps。光源和探测器之间间距设定为0.5 m,在中继墙面分别对应于直径为7 cm和10 cm的圆形照射或采集区域A和d,与中继墙面的距离14为20 m。为了模拟随机噪声的影响,在计算得到信号的基础上增加了10 dB的随机噪声。图6所示为仿真得到的光子飞行时间信号,其中实线代表原始信号,虚线代表经过传统的高斯拟合方法处理后的光子飞行时间信号。
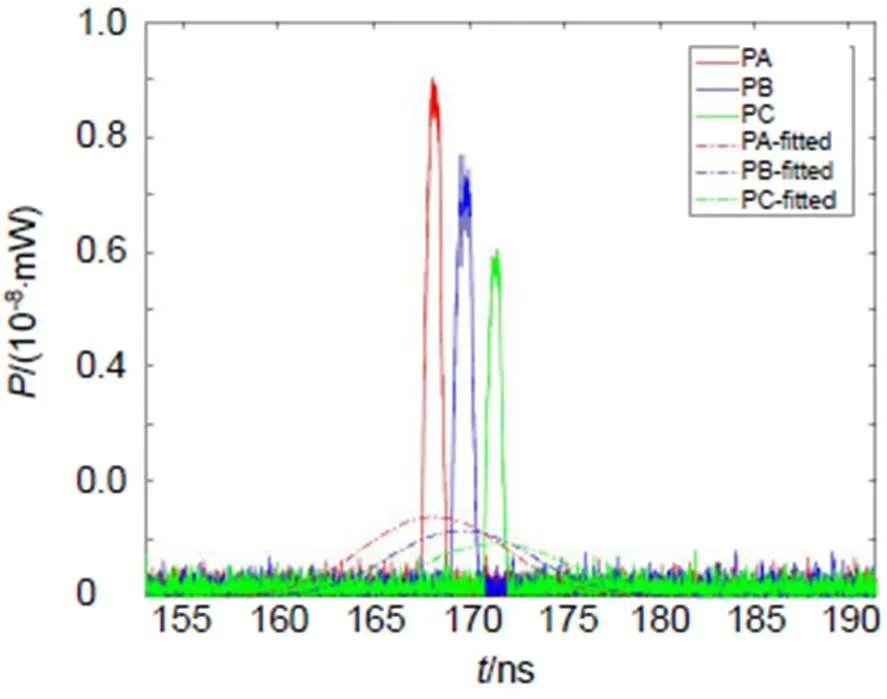
图6 仿真中三个探测器的信号
光子飞行时间与非视域光程直接相关,以某时刻信号强度作为该时刻对应光子飞行时间的概率,这样就可以根据非视域空间内各个位置对应的非视域光程来判断各个位置物体存在的概率。将三个探测器得到的数据转换为位置概率分布,同时投影到非视域,就得到了物体分布的联合概率密度分布函数。
按照上述原理,具体的位置概率分布求解过程为:1) 计算非视域范围内各个位置对应的非视域光程。2)将光程除以光速得到各个位置对应的光子飞行时间。3) 查找探测器测得信号在该时间对应的强度。4) 每个位置对应的信号强度就可以认为是该位置存在物体概率的体现。
从图7可以直观地看出,高斯拟合的数据处理方法对提高非视域物体定位效果有明显的提升,但该方法存在计算量大的缺点,以及受环境影响和人为选定信号处理区间的矛盾。
4 光子飞行时间提取算法对比
为了避免上述数据处理方法的缺点,本节就当前主要的几种滤波算法对非视域定位过程中光子飞行时间提取的适应性做出比较,在得到概率密度分布图后对目标位置判定的加权法和最大值法进行比较和优化。
4.1 滤波方法对比及其参数影响分析
针对中值滤波、均值滤波和高斯滤波三种时域滤波方法提取光子飞行时间的效果进行对比,并以滤波区间作为参数研究了各种滤波方法对参数的依赖程度。式(7)~式(9)分别是均值滤波、中值滤波以及高斯滤波三种方法的原理。
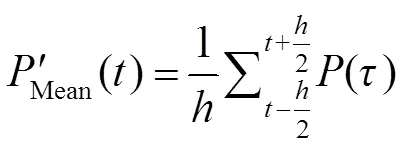
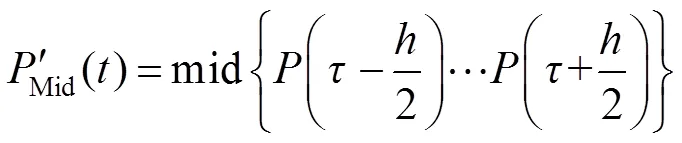

图8为使用三种滤波器提取光子飞行时间得到的定位误差随滤波区间的变化。可见对于均值滤波和中值滤波这种平滑性能较强的滤波器,如果取较小的滤波区间,则无法起到滤除噪声、精确提取光子飞行时间的作用;较大的滤波区间可能会使原信号失真。尤其中值滤波对区间大小更为敏感。均值滤波和中值滤波适宜的滤波区间宽度可以分别取1 ns和0.6 ns。高斯滤波器对于区间长度的要求较低,稳定性较好,为了提高运算效率可以选择1.3 ns作为滤波区间。
4.2 位置判定方法比较
在传统非视域定位方法选择概率密度极大值作为测量结果,称为最大值判定法,但这个结果很可能受到噪声或随机脉冲的影响,所以划定了概率阈值,利用阈值内各位置坐标及其概率加权得到物体位置,称为加权判定法。首先,将概率密度以极大值为标准进行归一化,接着选定一个概率阈值并筛选出满足概率阈值的位置坐标,最后对筛选得到的位置坐标以归一化概率密度为权重进行加权平均,进而获得被测物体位置坐标的期望。加权判定的定位结果解算方法和满足概率阈值区域的选取方式如式(10)和式(11)所示。
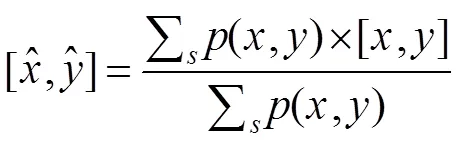
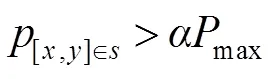
其中:(,)是位置[,]处对应的概率密度,[x,y]Î是区域内的概率密度,max是联合概率密度分布中概率密度的最大值,是给定的概率阈值后概率密度大于该阈值的区域,是概率阈值对应的归一化概率密度。为了研究概率阈值选取对定位效果的影响,此处选取4.1节中得到的1 ns、0.6 ns和1.3 ns分别作为均值、中值和高斯滤波算法的滤波区间参数,研究概率阈值的选取对定位精度的影响。
由图9所示,当阈值较小时会引入较多位置偏差大的区域,其中中值滤波和均值滤波分别在概率阈值为0.99和0.98时得到最小的定位误差0.0986 m和0.0568 m,均大于最大值判定法得到的0.0323 m和0.0316 m。可见中值滤波和均值滤波得到的位置精度会因为阈值的引入而低于最大值判定法的定位精度。高斯滤波光子飞行时间提取法在选取阈值为0.98时使用加权判定法的定位误差为0.0305 m,相比最大值判别法的0.04 m减小了24%。

图7 定位结果对比。(a) 原始数据的定位结果(4.443, 0.470);(b) 高斯拟合的定位结果(4.260, 1.400)

图8 滤波区间与定位精度的关系
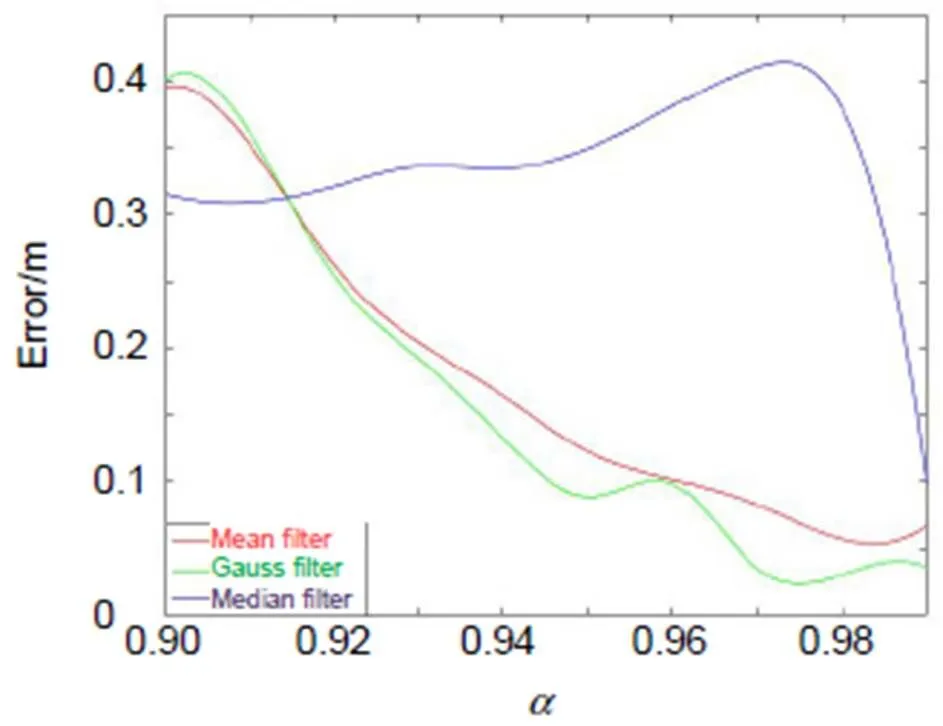
图9 概率阈值与定位精度的关系
4.3 滤波方法对几何参数适应性研究
光源及探测器之间的距离决定了椭圆概率分布的焦点距离。距离受应用环境的限制,但太小时得到的三个椭圆概率分布也越相似。当三个椭圆概率分布相似性提高时,交点位置也越模糊,定位结果抗干扰性越差。图10是光子飞行时间提取方法对光源及探测器之间分布距离的适应性对比。

图10 设备间距与定位精度的关系
从上图可以看出,定位误差随间距的变化与定性分析是一致的。随着的增加,中值滤波算法得到的定位误差首先在0.25 m处出现了收敛的趋势,随后高斯滤波和均值滤波算法的定位结果在0.35 m和0.38 m处逐渐平稳,可见中值滤波算法更适用于狭窄环境中对非视域的定位探测。如果环境允许,=0.5 m可以作为一个更适合的间距,并且在该距离下定位误差对敏感度较低,定位的稳定性和可靠性也更高。
在非视域5 m×5 m范围内选取相邻两个坐标距离为1 m的25个坐标点作为测试对象,对测量精度和测量范围的关系进行研究。拟合方法及三种滤波方法的非视域定位在每个位置的定位误差如图11所示。图11中,滤波的光子飞行时间提取方法得到的定位效果明显优于拟合方法的定位。基于高斯拟合方法的非视域定位在该范围内的定位误差均值和标准差为0.3106 m和0.3010 m,均值滤波、中值滤波和高斯滤波的定位误差均值分别为0.0756 m、0.0735 m、0.0795 m,标准差分别为0.0422 m、0.0473 m、0.0283 m。可见中值滤波的平均定位精度最高,但相比平均定位误差最高的高斯滤波,稳定性较差,例如坐标(1,1)和(5,2)位置的定位出现了较大的失真。高斯滤波的定位算法虽然平均定位误差相对较大,但在稳定性上有明显优势。
5 有效性验证
上述部分仿真结果在距离为1.3 m(14=1.3 m)的实验环境(如图12所示)中得到了验证。实验选用波长为1550 nm的脉冲激光器,其峰值功率为10 W,重复频率为20 MHz,脉冲宽度为0.4 ns。单光子探测器选用超导纳米线(SNSPD)。计数器选用时间数字转换器(TDC),该计数器以光源随激光脉冲同步发出的电脉冲为时间零点,记录单光子探测器测得的光子数随时间分布情况。实验中探测器之间的间距为0.075 m(= 0.075 m),被测物体使用一块宽10 cm、高40 cm、厚2 cm的泡沫板代替。
实验中,被测物体分别放置于(0.47 m,0.31 m),(0.52 m,0.21 m),(0.46 m,0.41 m)三个位置。以位置(0.47 m,0.31 m)为例,三个探测器测量得到的返回光子数信号如图13所示。
这里分别使用传统高斯拟合方法和均值滤波、中值滤波、高斯滤波方法对实验信号进行光子飞行时间的提取。根据4.1节的滤波参数仿真分析,分别选用1 ns、0.6 ns和1.3 ns作为中值滤波、均值滤波和高斯滤波的区间长度。根据提取到的光子飞行时间得到的定位结果如表1所示。

图11 各种光子飞行时间提取方法对应的定位误差空间分布。(a) 高斯拟合;(b) 均值滤波;(c) 中值滤波;(d) 高斯滤波

图12 实验环境
从实验结果可以看出,传统的高斯拟合方法得到的定位误差较大,并且容易出现定位失真的情况(如位置2和3)。三种滤波的光子飞行时间提取方法较传统的高斯拟合提取方法更加稳定。根据实验结果对比,高斯滤波提取方法得到的定位精度更高,并且中值滤波方法得到的定位结果会出现定位失真的情况(如位置2)。
6 结论与展望
本文采用光度学的方法表征了光子飞行模型中的能量变化,并以该优化的光子飞行模型为基础对均值滤波、中值滤波、高斯滤波三种滤波器提取光子飞行时间的非视域定位效果进行了对比和分析,得出了以下结论:
均值滤波和中值滤波对滤波区间参数较为敏感,较小的区间无法起到滤波作用,较大的区间会损失原信号信息进而带来定位误差,高斯滤波算法的定位结果会随着区间的增大趋于稳定,在不考虑运算量的情况下可以选取较大的区间。设定概率阈值的加权位置判定法在高斯拟合的定位方法中可以降低定位误差,但不适用于均值滤波和中值滤波的定位方法。光源以及探测器之间的间距受使用环境的限制,在宽度小于1 m的狭窄环境中使用中值滤波算法可以获得更好的定位效果。当物体在给定范围内移动时均值滤波和高斯滤波的定位稳定性要优于中值滤波,但如果从误差均值体现的整体定位效果考虑,中值滤波更有优势。在实验中,三种滤波算法提取光子飞行时间的有效性得到了验证,并且进行了定位精度的对比。具体的实验环境中,被测区域不仅有待测物体,还有背景环境以及视线范围内杂物带来的背景信号。在从背景信号中提取目标信号时,可能会由于探测器或光源的不稳定性导致背景信号的不稳定,提取出的目标信号就含有较高的背景扰动。此时可以考虑时间选通的算法滤除掉探测区间对应光子飞行时间以外的信号,减少干扰。
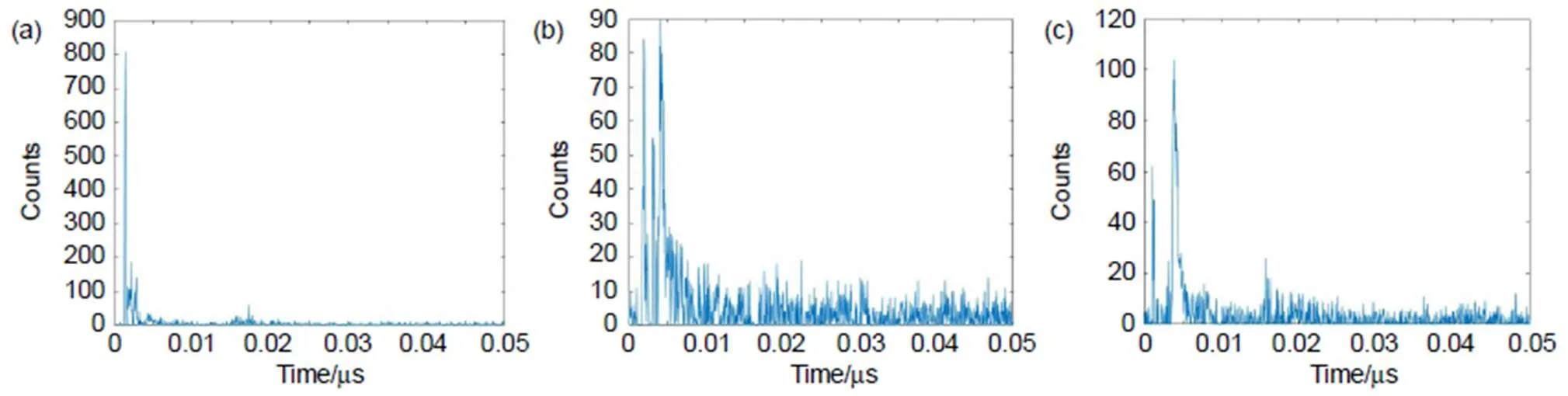
图13 当目标位于坐标(0.47,0.31)时三个探测器测得的原始数据。(a) 探测器A;(b) 探测器B;(c) 探测器C
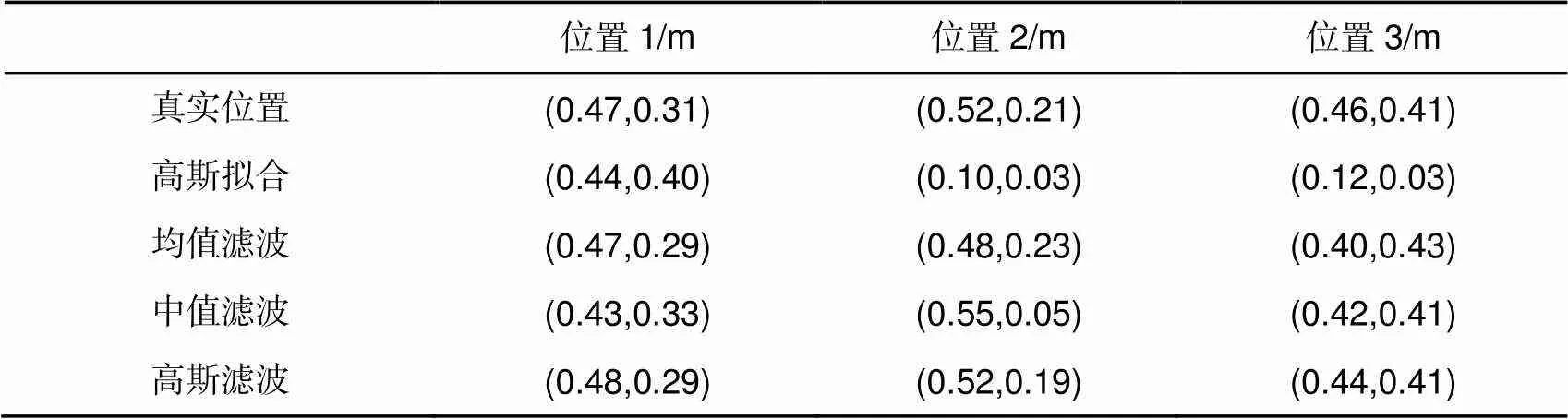
表1 多种光子飞行时间提取方法的定位结果对比
[1] Velten A, Willwacher T, Gupta O,. Recovering three-dimensional shape around a corner using ultrafast time-of-flight imaging[J]., 2012, 3: 745.
[2] Laurenzis M, Velten A. Nonline-of-sight laser gated viewing of scattered photons[J]., 2014, 53(2): 023102.
[3] Laurenzis M, Velten A. Feature selection and back-projection algorithms for nonline-of-sight laser–gated viewing[J]., 2014, 23(6): 063003.
[4] Buttafava M, Zeman J, Tosi A,. Non-line-of-sight imaging using a time-gated single photon avalanche diode[J]., 2015, 23(16): 20997–21011.
[5] Arellano V, Gutierrez D, Jarabo A. Fast back-projection for non-line of sight reconstruction[J]., 2017, 25(10): 11574–11583.
[6] Jin C F, Xie J H, Zhang S Q,. Reconstruction of multiple non-line-of-sight objects using back projection based on ellipsoid mode decomposition[J]., 2018, 26(16): 20089–20101.
[7] Klein J, Peters C, Martín J,. Tracking objects outside the line of sight using 2D intensity images[J]., 2016, 6(1): 32491.
[8] O'Toole M, Lindell D B, Wetzstein G. Confocal non-line-of-sight imaging based on the light-cone transform[J]., 2018, 555(7696): 338–341.
[9] Xin S M, Nousias S, Kutulakos K N,. A theory of Fermat paths for non-line-of-sight shape reconstruction[C]//, 2019: 6800–6809.
[10] Liu X C, Guillén I, La Manna M,. Non-line-of-sight imaging using phasor-field virtual wave optics[J]., 2019, 572(7771): 620–623.
[11] Gariepy G, Tonolini F, Henderson R,. Detection and tracking of moving objects hidden from view[J]., 2016, 10(1): 23–26.
[12] Chan S S, Warburton R E, Gariepy G,. Non-line-of-sight tracking of people at long range[J]., 2017, 25(9): 10109–10117.
A comparative study of time of flight extraction methods in non-line-of-sight location
Ren Yu1,2,3, Luo Yihan1,2*, Xu Shaoxiong1,2, Ma Haotong1,2, Tan Yi1,2*
1Key Laboratory of Beam Control, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institutue of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Sciences, Beijing 100049, China
Principle of the back projection algorithm
Overview:The detection of the information out of sight is always a difficult problem. It is valuable in complex scene such as autopilot and rescue. The casualty would be fewer if we obtain more decision time by getting the information of invisible area in advance. With the development of photoelectric technology, ultrafast lasers and detectors with high sensitivity and time resolution are invented, such as streak cameras, single photon avalanche diodes, superconducting nanowire single-photon detectors, and so on. It is possible to measure the time information of laser pulses in a photon by the single photon detector. The laser pulses can illuminate the scene of non-line-of-sight by bouncing on the relay surface and scattered back to relay surface again. The time of flight that pulses spent in the hidden area and the light intensity distribution on relay surface can be measured by the single photon detector, and the scene out of sight can be depicted from them. The back-projection algorithm, light-cone transform algorithm, Fermat flow and phase-field virtual wave optics have been proposed to calculate the scene out of sight. In order to obtain the light intensity distribution, the relay wall need to be scanned with the methods mentioned above and it is time-consuming. In most application environment, non-line-of-sight information needs to be acquired rapidly and the motion state of moving objects is more useful than their details. In the previous studies, the optical signal scattered by hidden targets is fitted into the Gauss distribution to extract the time of flight, and its position is figured out according to the time of flight. In this paper, we replace the Gauss fitting algorithm with the filtering algorithm to overcome its instabilities and improve the automation of that locating algorithm. Mean filter, medium filter and Gauss filter are proposed to improve the locating performance. In order to compare the characteristics of these three filters, the non-line-of-sight location is simulated with numerical simulation software based on the photon flight model which is optimized with photometry. Medium filter performs better than other two methods in a narrow application environment to obtain the more accurate locating result. For mean filter and Gauss filter, 0.5 m is a suitable distance between the laser source and detectors to locate the target reliable. As to Gauss filter, the position of target can be judged more accurately by probability weighting with an optimized threshold. The applicability of the fitting method and filtering methods are analyzed by comparing the locating error of 25 positions in the area of 5 m×5 m. Location information obtained by the Gauss fitting method is more stable than other two methods. In terms of the average of positioning error, medium filter performs better than other two methods. And the locating result of the fitting method is not accurate and stable as the filtering method.
Ren Y, Luo Y H, Xu S X,A comparative study of time of flight extraction methods in non-line-of-sight location[J]., 2021, 48(1): 200124; DOI:10.12086/oee.2021.200124
A comparative study of time of flight extraction methods in non-line-of-sight location
Ren Yu1,2,3, Luo Yihan1,2*, Xu Shaoxiong1,2, Ma Haotong1,2, Tan Yi1,2*
1Key Laboratory of Beam Control, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2Institutue of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;3University of Chinese Academy of Science, Beijing 100049, China
Non-line-of-sight location is an active detection technology which is used to detect the position of objects out of sight by extracting the time of flight. It is a research hotspot in recent years. In order to study the performance differences of mean filter, median filter and Gaussian filter in extracting time of flight, firstly, the energy changing model of photon flight model is optimized by photometry, and then the parameters of the three filtering methods are optimized and analyzed. After that, the adaptability of these three extraction methods to the maximum value judgment method and probability threshold weighted judgment method is analyzed. Finally, the accuracy and stability of these three time extraction algorithms are compared by using the positions of devices and invisible object as variables. The simulation results show that the median filter is suitable for a narrow environment and it has the high accuracy in positioning; the locations with Gaussian filter have good positioning stability and there is a wider selection range of filtering parameters when the signal is processed with Gaussian filter.
non-line-of-sight location; time of flight; filter algorithm; adaptability analysis
TN911.74
A
10.12086/oee.2021.200124
The Youth Innovation Promotion Association, CAS (2017428,2018411), State Key Laboratory of Pulsed Power Laser Technology(SKL2018KF05), and Excellent Youth Foundation of Sichuan Scientific Committee(2019JDJQ0012)
* E-mail: luo.yihan@foxmail.com; tandeman@126.com
任禹,罗一涵,徐少雄,等. 非视域定位中光子飞行时间提取方法对比研究[J]. 光电工程,2021,48(1): 200124
Ren Y, Luo Y H, Xu S X,A comparative study of time of flight extraction methods in non-line-of-sight location[J]., 2021, 48(1): 200124
2020-04-14;
2020-06-02
中国科学院青年创新促进会(2017428,2018411);脉冲激光技术国家重点实验室(SKL2018KF05);四川省科学委员会优秀青年基金(2019JDJQ0012)
任禹(1994-),男,硕士研究生,主要从事非视域探测领域的研究。E-mail:yuren_ioe@163.com
罗一涵(1982-),男,研究员,主要从事弱目标探测等领域的研究。E-mail:luo.yihan@foxmail.com
谭毅(1977-),男,研究员,主要从事光束控制关键技术等领域的研究。E-mail:tandeman@126.com

