无人机传感器故障诊断系统的数据预处理方法研究∗

强明辉 郭 俊

（1.兰州理工大学电气工程与信息工程学院 兰州 730050）（2.甘肃省工业过程先进控制重点实验室 兰州 730050）（3.兰州理工大学电气与控制工程国家级实验教学示范中心 兰州 730050）

1 引言

无人机广泛应用于国民经济的各个领域，无人机飞行安全越来越受到人们的广泛关注。传感器是测量无人机姿态信息的核心，传感器为无人机的飞行提供安全、可靠、全面的数据信息［1］。无人机的安全飞行很大程度上取决于传感器是否故障。而无人机经常会飞行在具有强干扰、强震动等恶劣的环境中，因此，传感器的工作状态会受到一定程度的干扰［2］。尤其是用于惯性导航的加速度计和陀螺仪等传感器，使传感器回传给控制系统的数据信息发生异常波动，波动幅度过大会造成故障诊断系统的误报警，向无人机飞行控制系统提供了不准确的数据信息［3］。为了保证传感器检测数据信号的准确性，需要对传感器输出的数据信息进行预处理，去除掉其中的噪声信号，减小故障诊断系统的误判率。

本文在研究了中值滤波、小波滤波优缺点后，改进小波滤波阈值函数，并将中值滤波和改进的小波滤波相结合的滤波方法，对惯导传感器中采集到的数据进行处理，消除脉冲噪声和随机噪声带来的影响，取得了良好的过滤效果。

2 数据预处理方法

针对无人机在飞行过程中陀螺仪和加速度计等传感器容易受到外界温度、电磁等因素的影响，使自身输出信号中含有大量的随机噪声信号，影响故障诊断系统的判断。改进了小波滤波阈值函数，设计了中值滤波和改进的小波滤波相结合的滤波方法，对无人机传感器检测的数据信息进行预处理。其数据预处理流程如图1所示。

2.1 中值滤波算法

中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值［4］。中值滤波的基本原理是把数字序列中一点的值用该点的一个邻域中各点值的中值代替，让周围的数字值接近的真实值，从而消除孤立的噪声点。对于传感器检测的参数序列，可以采用中值滤波方法，有效滤除脉冲干扰［5］。

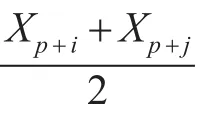
2.2 小波滤波算法

小波变换是信号分析的一种形式，小波分析是将信号分解成一系列小波函数的叠加，这些小波函数是由一个母小波函数经过平移与尺度伸缩得来的［7］。用不同压缩尺度的小波函数与信号比较获得相似系数，最终遍历整个信号，完成小波变换。这样用不规则的小波函数来逼近尖锐变化的信号能够得到信号更好的局部特性［8］。一般通过信号函数与小波函数的内积来表示小波变换，如式（1）。

式中ψa'b表示基本小波函数，a为尺度因子，改变小波的形状，b为位移因子，改变小波的位移。

但是在每个可能的缩放因子和平移参数下计算小波系数，其计算量相当大，将产生惊人的数据量，而且有许多数据是无用的。所以在离散小波变换中将缩放因子和平移参数都选择为2j的倍数，可以有效降低数据量。离散小波变换中，Mallat滤波算法应用最为广泛。该算法利用高通和低通滤波器，将信号分解为一个近似值A和一个细节值D。在使用实际滤波器对真实信号进行变换时，根据尼奎斯特采样定理，得到离散小波变换的近似系数cA和细节系数cD［9］。小波分解过程如图2所示。

图2 小波分解过程

在小波域，有效信号对应的系数一般比较大，而噪声信号对应的系数较小［10］。所以在获得各尺度系数之后，低频系数直接置零，只针对高频信号进行阈值处理。通过这种方法能够有效去除信号中存在的随机噪声，并且只对原始信号的特征产生较小的影响［11］。最后利用最底层低频系数和每一层的高频系数进行小波重构，获得去噪之后的信号。

小波去噪需要进行小波基函数与分解层数的选择、阈值函数与门限值的选取，其中小波基函数与分解层数选择相对固定，而针对高频系数选取的不同阈值函数处理方式往往对小波去噪效果的影响比较大。传统的阈值函数主要有硬阈值函数（2）和软阈值函数（3）：

2.3 改进阈值函数的小波去噪

硬阈值函数直接通过判断系数与阈值的大小进行赋值，在均方误差意义上优于软阈值法，但是因为硬阈值函数在ω=λ处不连续，所以信号在改点会产生附加震荡，产生跳跃点，不具有原始信号的平滑性。软阈值在判断了系数值大于阈值之后利用两者之差作为新的系数，软阈值函数估计得到的小波系数整体连续性较好，从而使估计信号不会产生附加震荡，但是会压缩信号，不利于重构后的信号向原始信号的逼近，会产生一定的偏差，直接影响到重构的信号与真实信号的逼近程度［12］。

本文结合软硬阈值函数在进行小波系数处理过程中存在的相关问题，采用新的小波阈值函数（4）进行小波系数的重构。

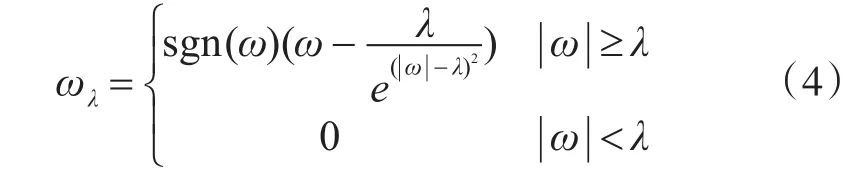
而该阈值函数需要满足以下几个方面的特征。首先，阈值函数在其定义域内要保证连续，这样才能够避免在重构的过程中出现震荡的问题；其次，阈值函数重构的信号应该能够无限地逼近原始信号，而在数学表达式中表现为其渐近线能够接近y=x这条线，这样可以避免在信号重构过程中出现较大的偏离［13］。

根据式（6）～（9）可知，新阈值函数渐近线的斜率为1，截距为0，渐近线为y=x，也就是说，重构的小波信号可以无限地接近原始信号。

3 仿真实验分析

为了验证改进阈值小波去噪的效果，本文先对硬阈值、软阈值和改进阈值去噪的实验结果进行分析。

在Matlab仿真平台上利用wnoise函数生成含有噪声的信号，其中信噪比设置为6。再利用小波滤波对该信号进行滤波，小波滤波的过程分别选择硬阈值、软阈值与改进阈值函数，对比三种不同的阈值函数的滤波效果，同时利用均方误差和信噪比对滤波效果进行比较，观察三种不同阈值函数的差异。

式（10）和（11）分别为信噪比和均方误差计算公式。

其中，yi表示原始信号，表示去噪之后的信号，信噪比和均方误差能够反映信号去噪效果，信噪比越大说明混在信号中的噪声越少，而均方误差越小，说明去噪之后的信号与原来的信号能够更加接近，信号精度更高。

3.1 不同阈值函数的小波去噪效果比较

在进行小波处理的过程中，为了验证阈值函数的效果，确保其他的变量都保持一致，其中小波基函数选择sym6，小波分解层数选择6层，小波阈值函数门限值

图3 原始信号

通过图像观察发现，三种滤波方式都能够起到较好的滤波效果，可以去除大多数的随机噪声信号。但是硬阈值和软阈值滤波方式存在着较大的均方误差，信噪比较小。而改进阈值明显均方误差较小，信噪比较为突出。所以改进阈值函数的小波滤波具有更好的去除随机噪声的效果。同时，在三种滤波图像中，通过观察横坐标470和890附近可以看出，改进的阈值函数能够保留更多的原始信号的细节，而硬阈值和软阈值函数的去噪过程中都没有被保留下来，或者效果不够明显，说明在信号的还原度方面，改进阈值函数也存在优势。

图4 加入噪声的信号

图5 改进阈值函数滤波信号

图6 软阈值函数滤波信号

图7 硬阈值函数滤波信号

表1 不同阈值函数的处理结果

3.2 混合滤波的效果验证

通过上述的分析，本文验证了改进阈值函数的小波滤波在处理随机噪声中的效果，既能够避免硬阈值带来的数据震荡，又能够防止软阈值出现的信号失真，在保证信号连续的过程中更好的还原信号。在对无人机导航传感器进行数据预处理的过程中，可以将其与中值滤波结合，去除数据中含有的脉冲噪声和随机噪声。本文含噪信号的产生模型可以用f(t)=x(t)+n(t)+p(t)来表示，其中x(t)表示通过模拟无人机飞行产生的飞行传感器数据，这里用经度位置来代替，n(t)是利用Matlab仿真软件中的wnoise函数生成的随机噪声信号，p(t)是在固定位置加入的脉冲信号。

图8 传感器原始经度信号

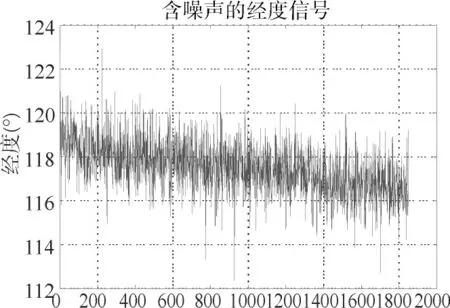
图9 含有噪声的经度信号

图10 混合滤波处理后的经度信号

图11 中值滤波处理后的经度信号

图12 改进阈值函数的小波滤波处理后的经度信号

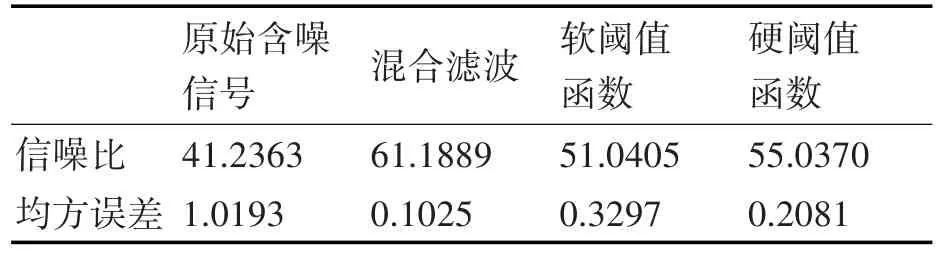
表2 不同滤波对传感器数据处理的结果

通过对信号图像和数据的分析本文发现，只通过中值滤波能够去除信号中含有的脉冲噪声，但是对随机噪声去除效果不明显，而只通过小波滤波能够去除其中大部分的随机噪声信号，并且对脉冲噪声有一定的抑制作用，但是脉冲噪声去除并不彻底，同时在滤波的过程中受到脉冲噪声的干扰，容易出现信号的失真现象，偏离原始信号较多。而通过混合滤波既能够去除其中的脉冲噪声，又能够很好地过滤随机噪声，同时在还原信号的过程中更加接近原始信号。再对三种滤波方式的信噪比和均方误差的比较发现，混合滤波的效果更佳。

4 结语

针对无人机导航传感器在工作的过程中其数据中容易掺杂大量的随机噪声和脉冲噪声。在进行故障诊断的过程中，这些噪声容易引起系统的误报警，所以针对这一问题，本文研究了无人机传感器数据预处理方法，对中值滤波、小波滤波和改进小波滤波方法就行了分析研究，经过仿真分析，效果不够理想。最后，采用中值滤波和改进小波滤波相结合的混合滤波方法，仿真结果表明，该方法可以更好地去除检测数据噪声干扰，提高了传感器检测数据处理的精度和可靠性。