微扰动和混合变异的差分生物地理学优化算法
葛 强,李玉晶,乔保军,左宪禹,王更科
(1.河南大学 数据与知识工程研究所,河南 开封 475004;2.河南大学 河南省大数据分析与处理重点实验室,河南 开封 475004;3.中国科学院 空天信息创新研究院,北京 100101;4.中国科学院 中国科学院大学,北京 100101)
0 引 言
生物地理学优化算法是由Simon教授等[1]基于生物地理学数学模型提出的一种群智能优化算法。BBO不同于其它群智能优化算法之处在于其主要通过迁移算子来实现各个栖息地之间的资源通信,并通过变异算子来提高种群的多样性。BBO算法在提出之后便得到了国内外智能优化算法研究学者的密切关注,众多学者将其应用到实际工程优化问题的求解中,如电力系统[2]、图像处理[3]、模式识别[4]、排列流水间调度[5]等。BBO算法的优点是收敛速度快、结构简单,但寻优后期易过早收敛,陷入局部最优。针对这一缺点,众多学者从不同的角度改进BBO算法来提高优化性能。王雅萍等[6]发现基于双曲正切函数迁移率模型的BBO寻优能力更强。郑夏等[7]引入Fibonacci迭代思想来消除种群重复项,差分进化来改进变异策略。张文辉等[8]提出基于自适应迁移算子和差分变异策略的BBO。唐继勇等[9]提出动态选择迁入地与自适应迁入策略。这些对BBO算法的改进均在某种程度上提升了算法的寻优能力,但在收敛精度、收敛速度和稳定性上还有很大的提升空间。本文提出的MDEBBO算法采用差分变异策略和自适应的局部扰动因子作为新的迁移算子,并采用一种基于高斯变异和柯西变异的根据迭代次数自调整的混合变异算子。仿真测试实验数据显示,MDEBBO算法在收敛速度和寻优精度上的优势明显。通过将MDEBBO算法应用到对Richards模型的参数估计上,实验结果表明其在参数估计方面也有很好的表现力。
1 生物地理学优化算法
生物地理学是根据生物有机体在空间和时间上的地理分布对其进行研究的学科,探索了不同地理位置的生态系统中不同物种的迁移和突变。在BBO算法中,优化问题的可能解被称为栖息地(Habitat),每个栖息地都根据栖息地适应性指数(habitat suitability index,HSI)进行评估。其中,影响栖息地适应性指数的因素称为适应性指数变量(suitability index variables,SIVs)。BBO算法被用来处理实际工程问题时,首先随机产生n个栖息地作为最初解,然后使用迁移操作来实现栖息地之间的信息共享,并通过变异操作来增加解的多样性,最后经过多次迭代操作获取最优解。
1.1 初始化
首先随机产生NP个可以表示为N维向量Hk(k=1,2,…,NP) 的候选个体,Hk(SIVj)(j=1,2,…,N) 表示为栖息地Hk的第j个SIV,Hk(SIVj) 初始化如式(1)所示
Hk(SIVj)=H(SIVjmin)+rand(H(SIVjmax)-H(SIVjmin))
(1)
其中,H(SIVjmax) 和H(SIVjmin) 分别为第j维变量的最大、最小限度。
1.2 迁移操作
在BBO算法中,栖息地通过迁移操作与其它栖息地共享信息。一个HSI值高的栖息地比HSI值低的栖息地容纳更多的物种。将栖息地Hk按HSI值以优至劣的顺序排序,栖息地Hk的物种数量按式(2)映射获取
Sk=Smax-k
(2)
其中,Smax为栖息地最多可生存的物种数量。在BBO中,每个栖息地都有各自的迁入率λ和迁出率μ,这两个参数控制着物种从一个栖息地向另一个栖息地的迁移。如式(3)和式(4)[7]所示,迁入率和迁出率取决于栖息地的物种数量
(3)
(4)
其中,I、E分别表示最大迁入率、最大迁出率,Sk为栖息地Hk的物种数量。首先根据迁入率λk挑选进行迁移操作的栖息地,然后对栖息地Hk的每个SIV根据迁出率μk按轮盘赌选择法获取待迁出的栖息地。最后按式(5)[7]完成迁移操作
Hk(SIVj)←Hm(SIVj)
(5)
其中,Hk(SIVj) 和Hm(SIVj) 分别为迁移栖息地和待迁出栖息地的j维分量。在BBO算法中,迁移算子的每次调用都会导致单个SIV从一个栖息地迁移到另一个栖息地中[10]。
1.3 变异操作
除了迁移,BBO还具有大多数进化算法所具有的概率特性,在算法的迭代过程中可能会发生突变[11]。变异算子根据栖息地存在的先验概率随机修改栖息地的SIV,其中栖息地Hk的物种概率Pk可由式(6)计算得出

(6)
通过对生物地理学分析得知,栖息地的突变概率mk和物种概率Pk成反比,栖息地Hk的突变概率mk如式(7)[12]所示
(7)
其中,mmax是栖息地Hk的最大突变概率,Pmax是所有物种概率的最大值。对于每个栖息地Hk,若随机数rand不大于该栖息地的突变率mk, 则随机选取一个规定界限内的值来替换栖息地Hk的某维解变量Hk(SIVj)。 BBO算法流程如图1所示。

图1 BBO算法流程
2 基于微扰动和混合变异的差分生物地理学优化算法
群智能优化算法的过程一般由勘探和开发两部分组成,勘探就是在全局找到最优解可能出现的大致位置的过程,而开发则是在局部最优解附近进行精确搜索的过程[13]。为了增强生物地理学优化算法的优化能力并克服该算法不能很好平衡开发能力与局部最优解之间的矛盾,本文从迁移率模型、迁移算子、变异算子3个方面改进,下面进行详细介绍。
2.1 非线性迁移率模型
BBO通过迁移操作实现栖息地之间的资源共享,迁入率、迁出率是决定栖息地进行迁移操作的主要因素,故不同的迁移率模型会直接影响该算法的寻优能力。文献[6]介绍了3种新的非线性迁移率模型,并将其应用到BBO算法中。实验结果表明越倾向于自然法则的模型越能提高算法的性能且基于双曲正切变体迁移率模型的BBO算法比余弦迁移模型寻优能力强,其解更接近函数的全局最小值,故本文选取如图2所示的双曲正切变体迁移率模型。
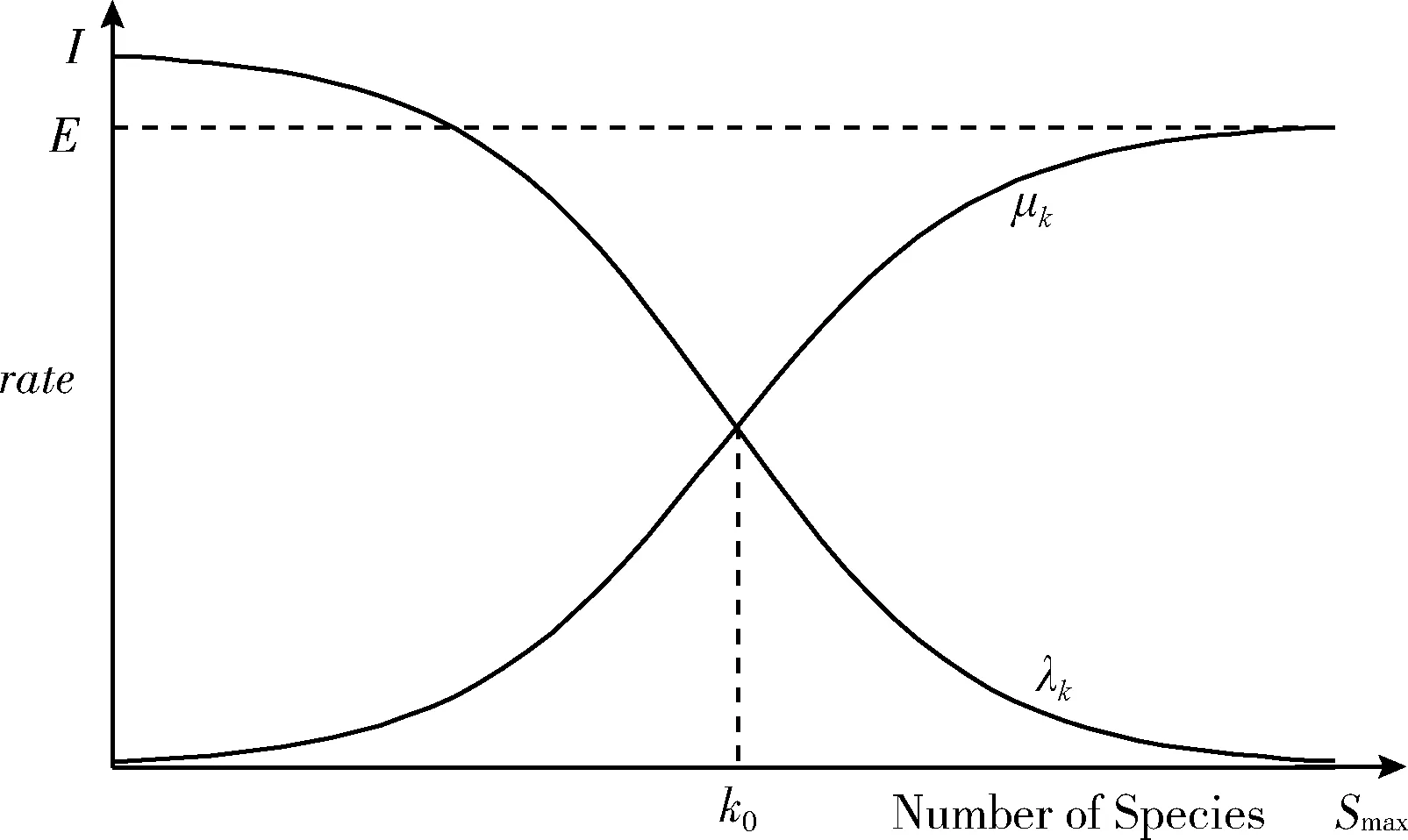
图2 双曲正切变型迁移率模型[6]
从图2可以看出,在双曲正切变型迁移率模型下,栖息地中物种数量相对较少或较多时,迁移率变化较余弦迁移率模型平缓些,当该栖息地中的物种数量增加到一定程度后,迁移率变化速率随之变快。双曲正切迁移率模型的迁入、迁出率表达式分别如式(8)、式(9)所示,其中a为迁移率模型的影响因子,n为栖息地Hk的物种数量,文献[6]将其取值为1.1,I和E分别为分别表示最大迁入率、最大迁出率
(8)
(9)
2.2 局部扰动和差分迁移算子
低开发能力和陷入局部最小化可以被认为是标准BBO的弱点,迁移算子的改进是增强算法优化能力的最佳方法之一。差分进化算法(DE)是一个优秀而强大的进化算法,它的一些差异策略提供了出色的全局搜索能力,引起了众多学者的广泛关注。通过分析式(5)得知,BBO的迁移算子只是栖息地之间SIV的简单替换,这种迁移方式单一,导致进化过程中影响算法的探索性能。在DE的启发下,MDEBBO将DE的变异策略引入到迁移算子中,新的迁移算子如式(10)所示。其中,Hbest是当代种群中HSI值最优的栖息地,Hindex1、Hindex2、Hindex3、Hindex4是从种群中随机挑选的4个栖息地,且满足index1≠index2≠index3≠index4≠i,F为缩放因子,通常取值为0.5。Hk(SIVj) 的某些信息来自Hbest, 因此Hk的位置能够快速移动到搜索空间中的最佳位置,而且可从4个不同的栖息地获取多样化信息,增加了种群的多样性。在迭代后期,BBO算法的种群多样性会随着寻优过程中逐步收敛而减小,且陷入局部极值的可能性增大
Hk(SIVj)=Hbest(SIVj)+F*(Hindex1(SIVj)-Hindex2(SIVj))+F*(Hindex3(SIVj)-Hindex4(SIVj))
(10)
为了进一步提高全局收敛精度,避免算法陷入局部极值,本文引入了一个微扰动算子来优化算法的性能。微扰动算子如式(11)所示
(11)
其中,σ为微扰动算子,Hi为轮盘赌方式选择的待迁出栖息地,Gindex为当前迭代次数,Gmax为算法的最大迭代次数,rand(0,1) 表示从0到1的随机数。由σ可以得到一个介于-0.5到0.5之间的随机值,将这个随机值作为权重与Hi和Hk之间的差分值相乘,得到扰动值。该策略通过引入正弦函数使σ的取值更具灵活性,可以实现以Hi(SIVj) 为中心的空间的精确搜索,提高算法的查找精度。在满足BBO迁移规则的基础下,添加一个约束条件(rand<0.2),如果达到了条件则采用全局搜索能力更强的差分迁移算子(式(10))进行寻优,若不满足,则采用微扰动算子来进行迁移操作(式(11))。改进的迁移算子结合DE的全局搜索和微扰动算子的局部搜索,在整体上提高了算法的开发能力,又由于通过引入正弦函数得出的微扰动因子增加了种群多样性从而避免算法陷入局部最优,故能够很好平衡开发能力与局部最优解之间的矛盾。局部扰动和差分迁移算子如算法1所示,其中输入参数Population为种群,NP为种群大小,N为种群维数,λ和μ分别为栖息地的迁入率和迁出率,Pmod为栖息地修改概率;输出参数Population为经过迁移操作后的种群。
算法1:迁移算子算法
输入: (Population,NP,N,λ,μ,Pmod)
输出: (Population)
(1) fork=1 toNPdo
(2) ifrand>Pmod
(3) continue;
(4) end if
(5) forj=1 toNdo //根据λ判断Hk是否发生迁移操作
(6) ifrand<λthen
(7) ifrand<0.2 then
(8) 通过式(10)更新Hk(SIVj)
(9) else
(10) //根据μ选择待迁出的栖息地Hi
(11) ifrand<μthen
(12) 通过式(11)更新Hk(SIVj)
(13) end if
(14) end if
(15) end if
(16) end for
(17) end for
2.3 混合变异算子
BBO算法的突变算子是通过随机选取一个规定界限内的值来代替原栖息地的某维解变量。在这种策略下,虽然该算子可以生成不同的解,但现有的良好解很有可能会被随机产生的值破坏而影响算法的收敛速度。为了提高解决方案的质量,本文引用进化规划算法的高斯、柯西变异,将两种变异算子结合迭代次数设置一种新的自调整的混合变异算子。高斯分布、柯西分布的概率密度函数分别如式(12)、式(13)所示
(12)
(13)
其中,μ和σ2分别表示高斯分布的均值和方差,x(x∈R)和t(t>0)都属于尺度参数。当σ=1,μ=0时N(0,1)表示标准高斯分布, C(0,1) 表示标准柯西分布。在BBO算法中,高斯、柯西变异就是将一个服从其分布的随机扰动项加到栖息地的某一分量上。根据高斯分布和柯西分布的特点,本文引入自调整混合变异算子,以此来提升算法的寻优速度和精度。混合变异算子如式(14)所示,其中Gindex表示当前迭代次数,Gmax表示算法的最大迭代次数。该策略将迭代次数作为权重系数来控制高斯变异和柯西变异之间的比例。该变异算子可以随着进化过程自启发的动态更新,在迭代初期,Gindex较小,通过柯西变异会获取大幅度的变异步长,增加了候选解的多样性,引领候选解快速向全局最优解移动,避免算法陷入局部最优解。在迭代后期,Gindex较大,高斯变异杰出的局部探索能力使候选解在局部范围进行精确搜索,提高算法了的寻优精度。本文采取的变异策略只对整个种群中HSI值较差的后一半栖息地改变其适应性指数变量,以免变异算子破坏迭代周期内的较优解

(14)
混合变异算子如算法2所示,其中输入参数Population为种群,NP为种群大小,N为种群维数,mk为栖息地的突变概率;输出参数Population为经过变异操作后的种群。
算法2: 混合变异算子
输入: (Population,NP,N,mk)
输出: (Population)
(1) //只对整个种群中HSI值较差的后一半栖息进行突变
(2) fork=NP/2 toNPdo
(3) forj=1 toNdo
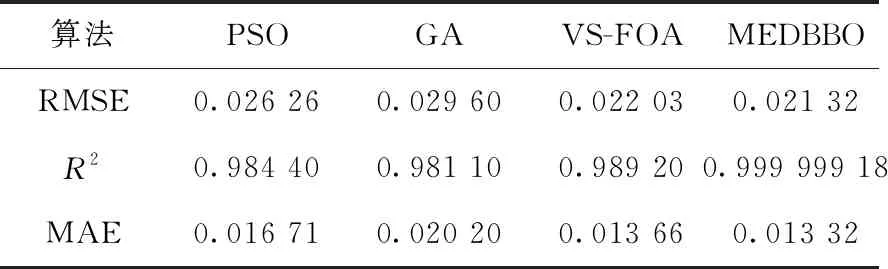
(4) ifrand (5) 通过式 (14) 更新Hk(SIVj) (6) end if (7) end for (8) end for 综上所述,MDEBBO算法的流程如下: MDEBBO算法步骤: 步骤1 初始化BBO参数:最大物种数量Smax, 最大迁出率E,最大迁入率I,最大变异概率mmax, 栖息地修改概率Pmod, 最大迭代次数Gmax, 种群大小NP,候选个体向量维度N等。随机生成NP个候选个体,并按式(1)计算其适应性指数变量SIVs。 步骤2 计算每个候选个体的适应性指数HSI值,并将种群按优至劣顺序进行排序。按式(2)计算每个候选个体可容纳的物种数量S,分别按式(8)、式(9)计算其迁入率λ和迁出率μ。保留该迭代周期内最优的两个候选个体作为精英个体。 步骤3 按算法1的迁移策略进行迁移操作。 步骤4 按式(6)计算候选个体的物种概率Pk, 按式(7)计算候选个体的变异率mk。 按算法2中的变异策略进行变异操作。 步骤5 重新计算候选个体的HSI值,将其重新进行排序。将保存的精英个体替换本迭代周期内最差的两个候选个体。 步骤6 判断是否达到终止条件,若是,结束并输出最优候选个体;若否,则跳到步骤2。 为了验证MDEBBO算法的寻优能力,通过对12个不同复杂度的基准函数进行大量的实验。实验分为两个部分,第一组实验是MDEBBO算法与经典、新型智能优化算法的对比,第二部分选取部分学者先进的改进算法与MDEBBO进行比较。 在这12个基准函数中,函数Sphere、Sumsquare、Rosenbrock、Schwefel1.2、Schwefel2.22属于单峰函数,Step是具有一个最小值且不连续阶梯函数,Quartic是一个噪声四次函数,多用来测试收敛速度和寻优精度;Ackley、Griewank、Penalty1、Penalty2、Levy是多模函数,其局部最小值随着维数的增加呈指数增长,多被用来测试算法避免局部最优解的能力以及全局探索性能。这12个基准函数已经被广泛用于不同的优化算法中以评估算法的性能。 在实验部分,本文所采用的硬件配置:CPU为2.0 GHz,内存24 GB的笔记本,实验所用操作系统为Windows10,编程语言采用MATLAB R2018a。本文中对算法的参数设置为:种群大小NP为50,维数N为30,栖息地最大变异概率Pmax为0.005,栖息地修改概率Pmod为1,最大迁入率I和最大迁出率E都为1,最大迭代次数Gmax为1000,精英个体保留数为2。ACO中信息启发式因子α为1,期望启发式因子β为5,局部信息素蒸发系数ρ为0.5,全局信息素蒸发系数q为0.9,CS中随机调整发现概率pa为0.25。BBO/DEs选取的是DE/best/2策略,其中F取值为0.5。因为算法运行存在一些不可控的随机因素,所以本文将每个函数独立运行30次来避免误差。本文选取最优值、平均值以及标准差3项来评估算法的性能。其中,最优值是算法找到的最优解;平均值是算法所有解的平均值,能够显示算法的优化精度;标准差能够体现算法的鲁棒性。 第一部分选取经典算法ACO(蚁群算法)、新型智能优化算法CS(布谷鸟搜索算法)、基本BBO和MDEBBO进行比较,结果见表1。其中,字体加粗的是算法结果中对应的最优项。根据机器对双精度实数的取值,精度大于 1e-15 的结果即被认为零[14]。由表1可以看出,MDEBBO算法在单峰、多峰函数上与其它智能优化算法相比,无论是最优值、平均值还是标准差都有很明显的数量级优势,且大部分函数最优解达到了函数的理论全局最优解0。对于函数Step、Schwefel2.22和Ackley,MDEBBO算法达到了最优值、平均值和标准差同时都为0,这说明迁移算子中加入微扰动因子,变异算子引入自适应混合变异思想可以提高算法的寻优精度。算法初始化具有随机性且标准差近乎为0,说明多次寻优结果的误差很小,即MDEBBO算法的探索能力优势明显,不易陷入局部最优。同时,4种算法在不同基准函数上的收敛曲线如图3所示,因为篇幅问题,本文只展示了其中6个不同类型的测试函数收敛图。收敛图中的横坐标为迭代周期数,纵坐标为最优适应度函数值。由图3中可以看出,其它智能优化算法在迭代后期中最优值下降速度明显缓慢,且迭代次数为200的时候就有陷入局部最优的趋势。而MDEBBO算法在迭代前期曲线近乎垂直,显示了其更强的勘探能力;且在迭代次数为100左右的时候就几乎达到了全局最优,展现了其优异的开发能力。综上所述,MDEBBO算法在收敛精度和收敛速度上都较不同智能优化算法有很明显的优势,在满足卓越开发能力的同时也避免了算法陷入局部最优。 为了进一步验证MDEBBO算法的寻优能力,第二组实验是MDEBBO算法与部分学者先进改进算法的对比,对比算法分别为基于双曲正切变型迁移率模型的BBO(MBBO)[6]、基于Fibonacci迭代的差分变异BBO(IDEBBO)[7]、基于自适应迁移和差分变异的BBO(SDBBO)[8],实验结见表2。由表2可看出,MDEBBO算法在最优值、平均值与标准差3个评价标准上都较其它3个改进算法有明显的优势。对于全域最小值附近平缓难以寻求最优值的病态二次函数Rosenbrock,MDEBBO算法的最优值结果比其它算法的求解精度有了一定程度的提升。对于具有一个最小值且不连续阶梯函数Step来说,改进的IDEBBO算法的最优值为0,但MDEBBO的平均值和标准差均为0,这说明MDEBBO算法通过微扰动因子、变异算子使算法的收敛精度和稳定性有大幅提升。多模函数常被用来测试算法避免局部最优解的能力,由表2可看出MDEBBO算法在多模函数上的寻优能力远远优于其它3个改进算法。同时,4种算法在不同基准函数上的收敛曲线如图4所示,MDEBBO算法的寻优能力在同类竞争力很强的先进改进算法面前也丝毫不逊色。 表1 不同优化算法对12个函数的测试结果 图3 不同优化算法对6个函数的收敛曲线 表2 不同改进BBO算法对12个函数的测试结果 图4 不同改进BBO算法对6个函数的收敛曲线 本节主要针对MDEBBO算法与传统BBO算法的计算复杂度进行理论分析。在传统BBO的迁移算子中,满足迁入率条件后需通过轮盘赌方式选择迁出栖息地,此时需要平均计算 (1+N)/2次。而在MDEBBO算法中,迁移算子添加了一个约束条件,若满足约束条件则不需要通过轮盘赌选择栖息地,而是通过DE的变异策略来进行迁移操作。若不满足约束条件则进行轮盘赌,此时平均计算次数小于等于 (1+N)/2次。MDEBBO算法的差分迁移算子中虽然多了一些判断步骤,但在数量级上并没有增加额外的复杂度。MDEBBO算法与传统BBO算法的变异算子的循环步骤一样,则计算复杂度相同。综上分析可得,MDEBBO算法不仅在收敛速度、精度提高的同时,计算复杂度并没有增加。 Richards模型是一个包含4个参数的非线性回归方程,该模型通过时间变化来描述生物的生长过程[15]。Richards模型的生长方程如式(15)所示,其用来描述生长过程中的增长量 (15) 其中,yt表示谷氨酸菌体在t时刻的生长浓度值,α表示该菌体生长浓度的饱和值,β表示初始生长浓度的值,γ表示生长速率参数,t表示时间间隔,δ描述谷氨酸菌体的生长曲线。通过MDEBBO算法对Richards模型进行参数估计,其中每个栖息地代表一个解,栖息地维度为4,即α、β、γ、δ这4个参数值。非线性参数估计的解决过程是在模型给定后,通过实际观测数据来估计各个参数的值。MDEBBO算法中的适应度函数用偏方平方和表示,如式(16)所示。实际观测值yi与预测值的差值越小说明拟合出来的函数越接近实际的值,即预测的参数越准确[16] (16) 以预测谷氨酸菌体生长浓度为例,使用MEDBBO算法通过仿真实验,计算出Richards模型中的参数α、β、γ、δ分别为0.8985、5.2206、0.6309、3.4197。由MDEBBO算法估算不同时刻谷氨酸菌体生长浓度与实际观测值之间的差值的平方和为0.009 091 1,这个值越小代表算法拟合的生长曲线越好,参数估计得越有效。图5表示的为由MDEBBO算法对Richards模型拟合的谷氨酸菌体生长曲线。从图中可以看出随着时间的增长,拟合的曲线与实际观测值之间的误差越来越小,表明了MDEBBO算法对参数估计的有效性和适用性。 图5 拟合的谷氨酸菌体生长曲线 为验证MDEBBO算法对Richards模型参数估计的适用性,本文选取多个算法和MDEBBO算法进行对比。将各个算法分别获取的谷氨酸菌体生长浓度预测值与实际观测值比较分析,实验结果见表3。其中对比算法包括粒子群优化算法(PSO)、遗传算法(GA)和变步长果蝇优化算法(VS-FOA)算法。表3中实际观测值和对比算法的预测数据均来自文献[15]。 表3 谷氨酸菌体生长浓度的实际观测值与不同算法的预测值 同时,本文将均方根误差(RMSE)、决定系数(R2)以及平均误差(MAE)作为评价指标来验证MDEBBO算法的有效性,其分别如式(17)~式(19)[17]所示 (17) (18) (19) 表4 不同算法基于不同评价指标的对比 由表4可看出MEDBBO在3个评价指标下的值更具优势,其预测精度、拟合优度、预测质量都较对比算法更高。这说明采用MDEBBO对Richards模型参数估计来预测谷氨酸菌体生长浓度更具有效性。 生物地理学优化算法作为一种新型的群智能优化算法,其全局搜索能力与避免早熟的性能方面仍有很大的进步空间。本文提出的MDEBBO算法通过在迁移阶段将差分变异算子和自适应的局部扰动操作结合形成新的迁移算子,增强了算法的全局探索能力;且通过高斯变异和柯西变异的混合变异算子来提高算法的开发性能和避免算法陷入局部最优解的能力。实验结果表明,MDEBBO较对比算法在收敛速度、寻优精度和稳定性3个方面都有很大程度上的提升。同时,通过仿真验证MDEBBO算法对Richards模型参数估计的适用性,对非线性模型的参数估计提供了一种新的方法。在接下来的工作中,重点是将BBO算法应用到对地观测卫星任务调度实际工程领域中并通过改进该算法来解决其全局优化问题。2.4 MDEBBO总流程
3 仿真实验与结果分析
3.1 测试函数与参数设置
3.2 与不同智能优化算法的比较
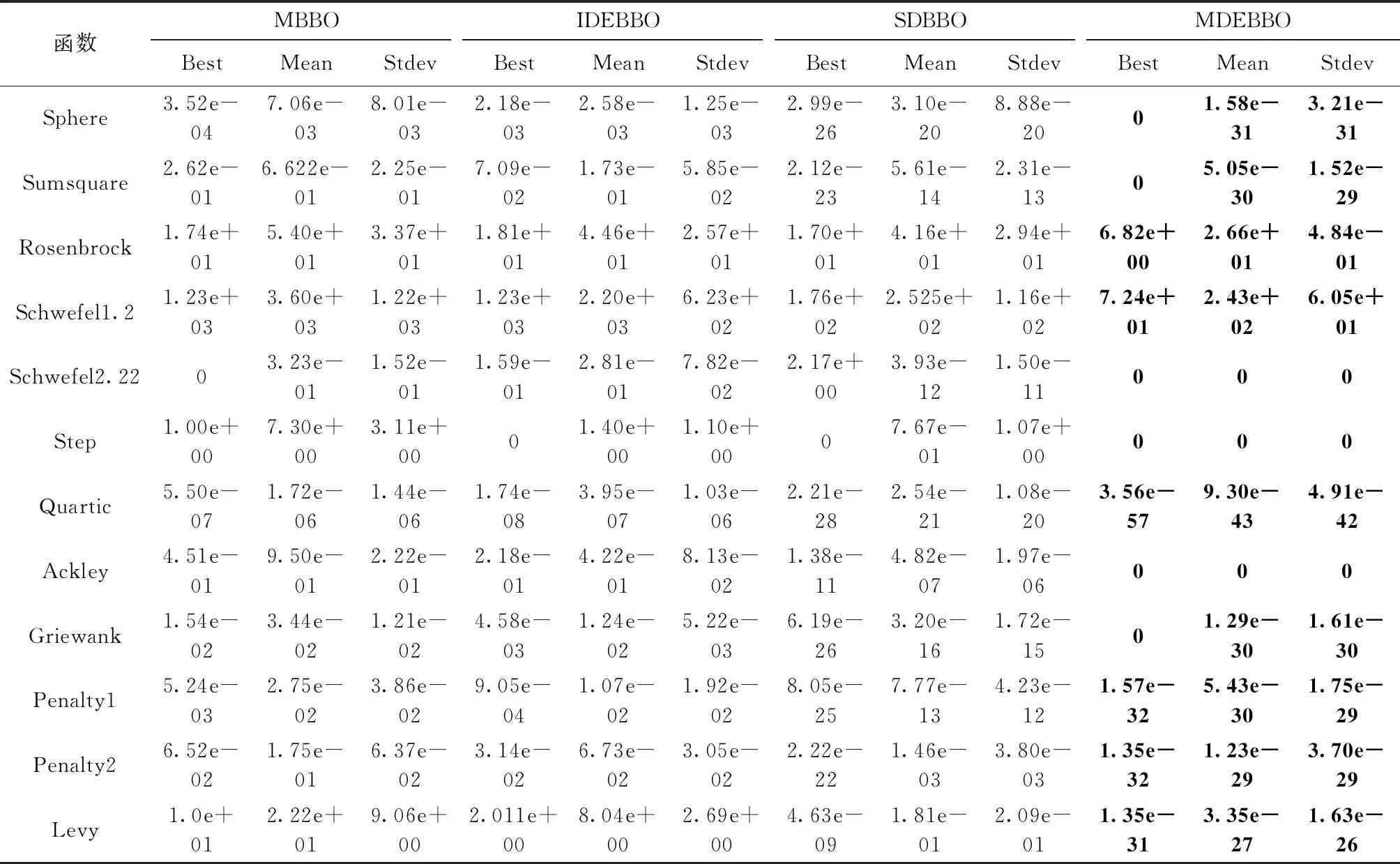
3.3 与不同改进BBO算法的比较



3.4 算法复杂度分析
4 Richards模型的参数估计



5 结束语

