1961—2017年长江中下游冬季降雪气候特征及其变化分析

董恒鑫，张子潞，张芯瑜，曾 燕，朱晓晨，邱新法，祝嗣嫄，米 鑫

(1.南京信息工程大学 应用气象学院，南京 210044；2.中国气象局交通气象重点开放实验室，南京 210009；3.江苏省气象科学研究所，南京 210009)

1 研究背景

在全球变暖变的大背景下，北半球中纬度地区极端降水事件频发，随之冬季强降雪出现频次增加[1]。长江中下游地区作为我国三大平原之一，地处三峡东部，是我国重要的电力、农业、交通运输等产业基地[2]，2014年，仅长江中下游地区第三产业增加12万亿元[3]。而冬季的强降雪则会对其产生极大影响[4-5]，在2008年年初因强降雪导致长江中下游地区大面积交通瘫痪，人员伤亡巨大，农作物绝收，直接损失更是高达1 516.5亿元人民币，极端降雪事件对农业、交通等产生巨大影响[6]。

目前，我国对降雪的研究主要针对大范围全国降雪趋势[7]及东北、内蒙古、新疆、青海、西藏等北部降雪频繁地区的降雪趋势[8-9]。李培基[10]主要利用影像数据等资料反演地表积雪情况；张灵和周月华[5]主要详细分析了湖北省降雪初雪异常的环流特征；雷向杰等[11]则研究了低温雨雪冻害的影响；秦艳等[12]、张良玉[13]的降雪研究主要针对天山、雄安等小部分地区，对我国中部地区的冬季降雪变化研究较少。而国外对于降雪变化的研究主要集中于气候模型[14]，以及由降雪而引发的二次气象灾害或者污染[15]等相关方面。

本文主要采用气候倾向率、M-K突变检验、累积距平法以及旋转经验正交函数(REOF)分析4种方法，对长江中下游地区冬季降雪变化进行诊断分析，以期对长江中下游地区冬季降雪变化特征和趋势有更深入的了解，为长江中下游地区的气象灾害分析提供技术支撑。

2 研究资料与研究方法

2.1 研究资料

长江中下游地区北至陕西、河南南部，西起湖北、贵州一带东部，南至湖南南部，东到江苏、上海。经纬度为24.5°N —34.5°N、106°E —122°E。

本文选取资料源于中国气象数据网的地面气候资料日值数据集V3.0，包含699个全国基准、基本站，并从中提取1961—2017年长江中下游地区118个常规气象站的冬季降雪数据(冬季降雪指的是当年12月份与次年1月份、2月份发生降水，且当日天气现象为降雪，视为降雪日)、平均温度、最高温度、最低温度，同时利用长江中下游地区基础地理数据，绘制常规气象站分布，如图1所示。

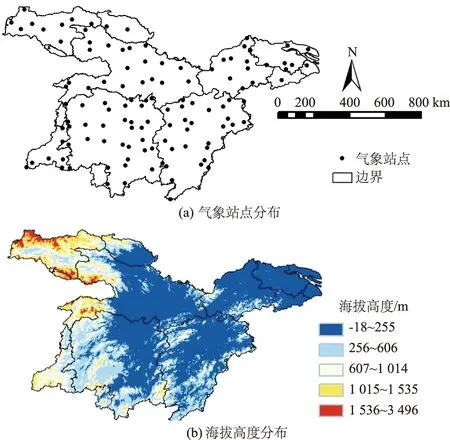
图1 长江中下游常规气象站点分布与海拔高度分布Fig.1 Distribution of conventional meteorological stations and altitude distribution in the middle and lower reaches of the Yangtze River

2.2 研究方法

2.2.1 气候倾向

气候倾向率主要用于冬季降雪要素的变化趋势，即式(1)，若气候倾向率呈现正值，则表示冬季降雪要素在该段时间内呈现增加趋势，反之则呈现减少趋势。

y(t)=b0+at。

(1)

式中：a为斜率，b0为截距；10a为气候倾向率(mm/(10 a))；t为时间序列；y为降雪要素。方程中的系数用最小二乘法确定。

2.2.2 累计距平法

累计距平[16]是气候趋势分析中的一种重要方法，主要用于反映降雪年际变化所具有的阶段性特征，其主要是在计算年距平的基础上，按照年份序列进行累加，进而得到累积距平，即

(2)

2.2.3 非参数M-K趋势分析法

非参数M-K(Mann-Kenddall)趋势分析是气象上常用的一种非正态分布数据的趋势分析方法[17]，该方法所分析的数据无需特定规律，其已广泛应用于气象、气候变化方面的研究。

非参数M-K趋势检验，通过定义检验统计量S，从而计算出标准正态分布统计量Z，S的具体计算公式为

(3)

式中：Xi、Xk分别表示第i个和第k个数据；i表示数据序列。

S为正态分布，其方差计算式为

var(S)=n(n-1)(2n+5)/18 。

(4)

当n≥10时，标准正态分布统计量计算公式为

(5)

双边的趋势检验中，在给定的置信水平上，若原假设是不可接受的，即在置信水平上，时间序列数据存在明显的上升或下降趋势。

Z>0则表示对于降雪变化来说呈上升趋势，而Z<0则表示降雪变化呈下降趋势;当|Z|≥1.28、1.64、2.32时则表示分别通过置信度为90%、95%、99%的显著性检验。

当M-K检验进一步应用于检验降雪序列突变时，检验统计量与上述Z略有不同，通过构造秩序列Sk(式(6))，并分绘制统计量UFk和UBk曲线(式(7)、式(8))。

(6)

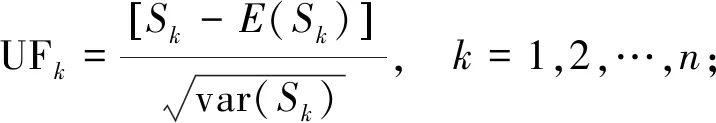
(7)

(8)

式中：k表示被统计的变量的序列;n为该序列最大值。

可以通过分析UFk和UBk两线的关系从而明确突变时间和突变区域。

若序列呈上升趋势则UFk>0；同理，若呈下降趋势则UFk<0；若超过临界值，则表示冬季降雪突变明显。如果UFk与UBk相交则表示该点为降雪突变发生的时刻。

2.2.4 旋转经验正交函数(REOF)

旋转经验正交函数(REOF)[18]是在经验正交函数(EOF)分析的基础上，其分析场达到一定的累积时，统计载荷矩阵，对极大方差进行旋转正交，最终得到方差的累积贡献。它可以使向量场进行调整，从而使得每一个点与一个主成分相关。该方法不仅能够保证整体的相关性，更能够清楚地反映局部变量之间的关系和分布情况。因此，本文在降雪要素分析上采用REOF方法对其进行分析，使原来特征结构简化，反映降雪气候特征更为明显，具体公式参照文献[18]。

2.2.5 反距离权重插值(IDW)

反距离权重插值法主要应用于估计插值点周围的观测点对该插值点的影响，且插值点与观测点之间的距离呈现反比关系，距离越近，权重则越大，反之越小，其计算关系为

(9)

式中：Z0是点(x0,y0)的估计值；Qi是插值点与观测点之间的权重系数，其计算过程为

(10)

其中，

(11)

式中：c为1或2，若c为1时，是反距离倒数差值，若c为2时，是反距离倒数平方差值；dk为观测点与插值点之间已知的距离的权重函数，k为观测点周围待插值点序列。

反距离权重差值是一种准确的、全局的差值方法，其差值结果与实际观测之间误差很小[19]，而本文中主要利用ArcGIS10.2中的IDW模块对本文的降雪、模态等空间分布进行插值计算。

3 结果分析

3.1 冬季降雪量分布特征

长江中下游地区西至巫山，东到黄海，而其冬季降雪量总体上呈现由东部向着西部减少的特征，如图2(a)所示，在25°N—30°N之间，湖南省与湖北省之间有一个降雪的高值区，且冬季降雪量在25 mm左右，其成因可能是从东部的冷空气长期受到湖南、湖北以西的山势阻挡，而造成降雪量上升，西部地区总体上冬季降雪量较少。

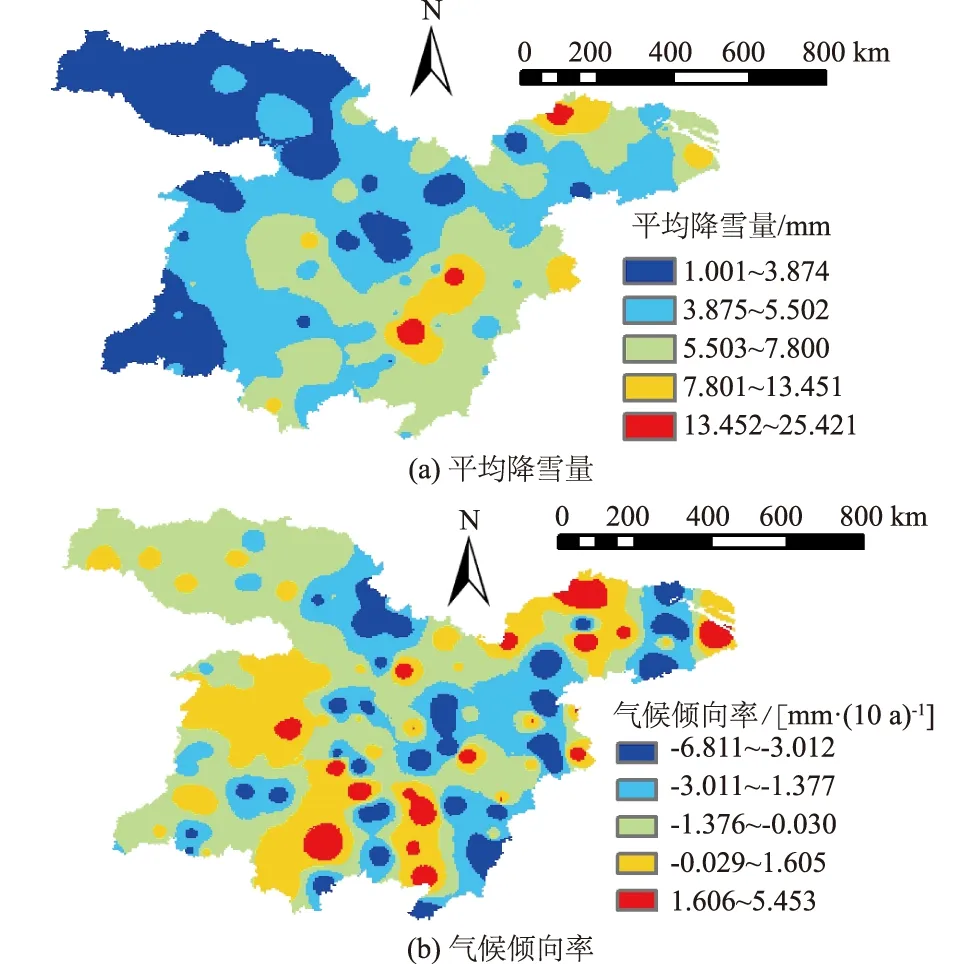
图2 1961—2017年长江中下游地区冬季平均降雪量与气候倾向率分布Fig.2 Distribution of average winter snowfall and climate tendency rate in the middle and lower reaches of the Yangtze River from 1961 to 2017

3.2 冬季降雪趋势及突变分析

3.2.1 冬季降雪趋势分析

由于气候变化的影响，长江中下游地区降雪量总体呈现逐年减少的趋势。图2(b)为1961—2017年长江中下游地区气候倾向率分布。从趋势图分析可见，长江中下游地区降雪趋势呈正变化趋势，主要集中在中部地区及南京一带，说明该区域冬季降雪量呈现上升趋势，最大倾向率为5.5 mm/(10 a)，而倾向率最小值主要集中在东部地区，且倾向率<0，说明东部地区的冬季降雪量正呈现逐年减少的趋势，最小倾向率为-6.8 mm/(10 a)。

3.2.2 冬季降雪突变分析

降雪突变分析是研究长江中下游地区冬季降雪状况发生转折的重要方式之一。由图 3(a)可以看出，UF和UB曲线在1985年左右出现交点，且在显著水平α=0.05的临界线内，说明降雪量在该年份出现突变且突变显著；从UF曲线可知，冬季降雪量在1961—1989年间一直呈现减少趋势，而在1990年后一直呈增加趋势，在1998年后该趋势达到显著状态。对比图 3(b)可以看出，1988年、1992年、2003年、2015年均为特征转折点，在图 3 (a)中1988年左右UF与UB曲线出现交点并通过了检验，可以确定1988年左右为降雪量由减少到增加的突变年份。

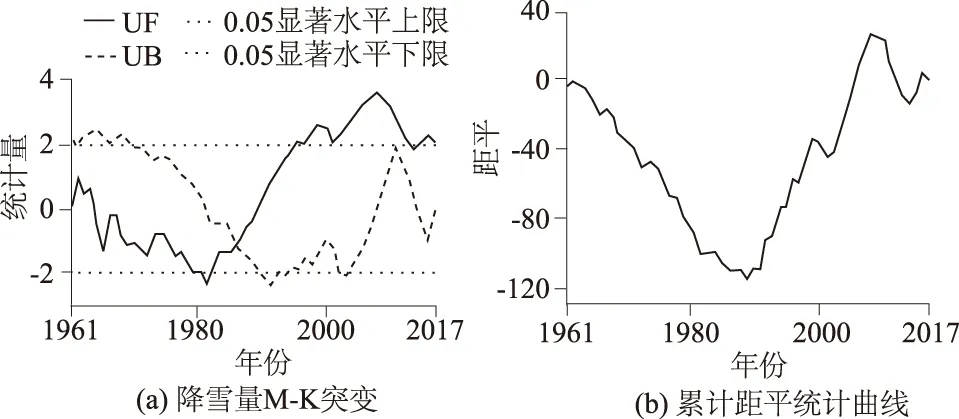
图3 1961—2017年长江中下游地区冬季降雪量M-K突变、累计距平统计曲线Fig.3 Statistical curves of M-K abrupt changes and cumulative anomalies of winter snowfall in the middle and lower reaches of the Yangtze River from 1961 to 2017

3.3 冬季降雪初、终、总日数特征分析

3.3.1 降雪初日特征分析

由图 4(a)可知，UF和UB曲线在1961—2017年间并未出现交点，说明57 a以来，长江中下游读取冬季降雪初日并未出现突变时间点；从UF曲线可知，自20世纪60年代以来冬季降雪初日一直呈现提前趋势，且1968年后该趋势达到显著。对比图 4(b)可以看出，1989年、2016年均为变化特征转折点，但在图 4(a)中并无交叉点，所以1989年和2016年并不是突变年份。

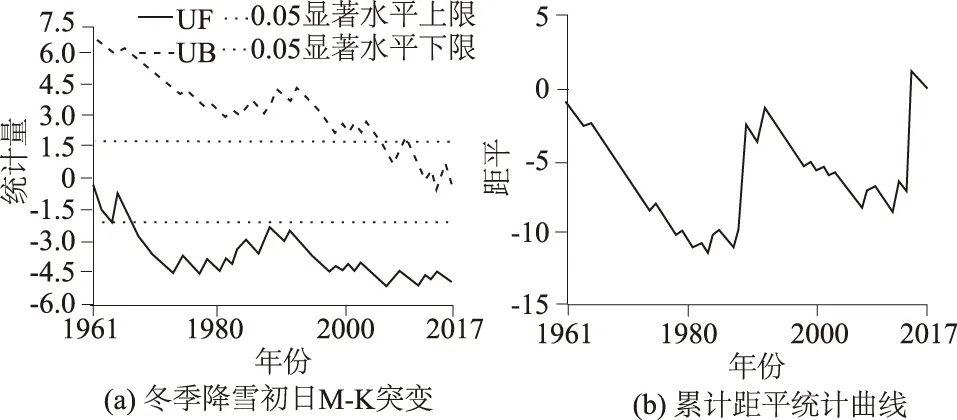
图4 1961—2017年长江中下游地区冬季降雪初日M-K突变、累计距平统计曲线Fig.4 Statistical curves of M-K abrupt changes and cumulative anomalies in the initial date of snowfall in the middle and lower reaches of the Yangtze River from 1961 to 2017

3.3.2 降雪终日特征分析

由图 5(a)可以看出，UF和UB曲线在1961—2017年间并未出现交点，说明57 a内长江中下游地区冬季降雪终日并未出现突变时间点；从UF曲线可知，自20世纪60年代以来冬季降雪初日一直呈提前趋势，且1970年左右之后该趋势达到显著。对比图 5(b)可以看出，57 a来长江中下游地区冬季降雪终日并未出现变化特征转折点，结合图 5(a)，可知57 a来长江中下游地区冬季降雪终日并未出现突变。

图5 1961—2017年长江中下游地区冬季降雪终日M-K突变、累计距平统计曲线Fig.5 Statistical curves of M-K abrupt changes and cumulative anomalies in the final date of snowfall in the middle and lower reaches of the Yangtze River from 1961 to 2017

3.3.3 冬季降雪总日数特征分析

由图 6(a)可以看出，UF和UB曲线在1982年左右出现交点，且在显著水平α=0.05的临界线内，说明降雪总日数在该年份出现突变且突变显著；从UF曲线可知，冬季降雪日数在1961—1968年呈减少趋势，在1969—1980年呈增加趋势，但两者趋势都不显著，自1981年后降雪总日数一直呈现减少趋势，且该趋势在1985年左右达到显著。通过对比图6(b)可发现，1981年、1985年、2012年、2015年均为曲线变化特征转折点，且在图 6(a)中1981年左右UF与UB曲线出现交点并通过了检验，可以确定1981年左右为降雪总日数由增加到减少的突变年份。

图6 1961—2017年长江中下游地区冬季降雪总日数M-K突变、累计距平统计曲线Fig.6 Statistical curves of M-K abrupt changes and cumulative anomalies in the total number of snowfall days in the middle and lower reaches of the Yangtze River from 1961 to 2017

3.4 降雪量REOF特征分析

3.4.1 空间变化特征

如表1所示，模态1、2、3、4、5均通过North判别准则，且前2个模态的方差贡献率较大且累计方差贡献率>85%，因此本文取前2个荷载向量场来反映1961—2017年长江中下游地区降雪特征。

表1 REOF分解后方差贡献率Table 1 Contribution rate of variance after REOF decomposition

其中模态1方差贡献率高达79.98%，远大于其他模态贡献率，该模态为长江中下游地区降雪主要空间分布形式。由图7(a)可见，第1旋转载荷向量场的高载荷区主要集中于长江中下游地区西北部(陕西、河南、湖北西北部等地区)，大约以大巴山脉为界，向北主要为正值区，向南主要为负值区，两处降雪变化特征相反，即北部降雪增多时，南部降雪会减少。由图7(b)得，模态2贡献率为5.90%，高载荷区同样主要集中于长江中下游地区西北部地区，呈现出典型的西北-东南逐渐下降趋势，反映长江中下游降雪量变化由西北向东南递减。

图7 1961—2017年长江中下游地区荷载空间分布的REOF分析结果Fig.7 REOF analysis results of spatial distribution of load in the middle and lower reaches of the Yangtze River from 1961 to 2017

3.4.2 时间变化特征

时间系数是衡量长江中下游地区冬季降雪随时间变化的重要指标之一，时间系数表示向量空间分布随时间的变化特征，而系数的符号则代表演变方向，正号则与模态方向一致，反之，表示相反。本研究对1961—2017年共57 a的降雪量进行分析。从图 8可以看出模态1与模态2均呈现下降趋势，表明长江中下游地区的冬季降雪总体呈下降趋势。

图8 1961—2017年长江中下游地区不同模态冬季时间系数变化Fig.8 Change of winter time coefficient in the middle and lower reaches of the Yangtze River from 1961 to 2017

4 相关性分析

影响冬季降雪特征变化的因素很多，本文通过相关分析，对长江中下游地区冬季降雪的气候倾向率、初日、终日、降雪量、降雪总日数与<2 ℃初日、终日日数及冬季平均气温的关系进行了检验，并结合冬季平均气温<2 ℃日数和降雪初终日期趋势变化对影响冬季降雪特征变化的因素进行分析。

从表 2、图 9可知，1961—2017年长江中下游地区冬季降雪初日、终日均与<2 ℃初日、终日呈正相关，但并未通过0.05显著性检验；降雪终日与冬季平均气温呈负相关而降雪初日与冬季平均气温呈正相关，但二者均未通过显著性检验；从1961—2017年冬季平均降雪量与<2 ℃初日、<2 ℃日数呈正相关，与<2 ℃终日、冬季平均气温呈负相关，其中<2 ℃日数通过0.05显著性检验，冬季平均气温通过0.01的显著性检验；降雪日数与<2 ℃初日呈负相关，与<2 ℃终日、<2 ℃日数、冬季平均气温呈正相关，其中<2 ℃日数与冬季平均气温通过了0.05的显著性检验。

表2 长江中下游地区降雪特征相关分析Table 2 Correlation analysis of snowfall characteristics in the middle and lower reaches of the Yangtze River

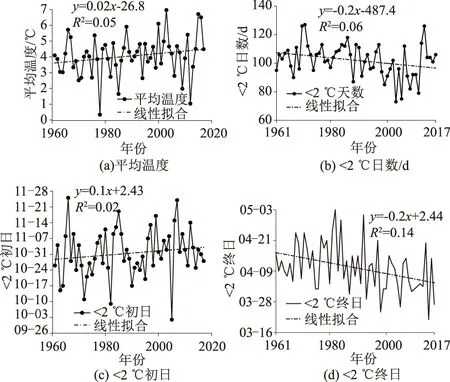
图9 1961—2017年长江中下游地区冬季平均气温、<2 ℃日数和初终日期趋势变化Fig.9 Trends of winter average temperature,days below 2 ℃,and initial and final dates below 2 ℃ in the middle and lower reaches of the Yangtze River from 1961 to 2017

5 结 论

本文从气候倾向分析、降雪量、降雪总日数、降雪初日、终日、相关分析以及REOF分析等方面，对长江中下游地区降雪进行分析，结论如下：

(1)长江中下游总体上中部、西部的冬季降雪变化呈现逐年增加趋势，而东部的降雪变化则呈现为逐年减少。

(2)经过M-K趋势检验和累计距平法的对比分析得出，在1961—2017年间，1981年为降雪日数由增加到减少的突变年，且1981年后降雪日数显著减少；1988年为降雪量由减少到增加的突变的年份；而降雪初日、终日未见明显突变。

(3)降雪量与<2 ℃日数、冬季平均气温呈正相关，降雪日数与<2 ℃日数、冬季平均气温也呈现正相关,得到降雪气候变化特征受冬季气温变化影响较大。

(4)REOF分析的长江中下游地区降雪量时空变化特征结果显示，长江中下游地区前2个模态累积方差贡献率高达85.88%，主要空间特征为由西北向东南逐渐减小，表明长江中下游地区降雪与降雪变化主要集中于西北地区。

本文研究基于历史资料对降雪进行了分析，对该地区已发生降雪事件有了全面的了解。下一步工作，笔者拟利用IPCC5气候情景模式数据，对未来的降雪发生发展做出进一步的研究与讨论。