拉盖尔-高斯光束调控冷原子自旋织构的数值分析
沈星, 孔令冉, 李睿宗, 张东方, 高天佑, 江开军*
(1 中国科学院武汉物理与数学研究所波谱与原子分子物理国家重点实验室, 湖北 武汉 430071;2 中国科学院冷原子物理中心, 湖北 武汉 430071;3 中国科学院大学, 北京 100049)
0 引 言
光偶极阱可以同时囚禁处于不同超精细内态的原子,形成旋量玻色-爱因斯坦凝聚体(BEC)[1],其自旋态存在诸多非平庸的空间分布,即自旋织构(Spin texture)[2],如狄拉克单极子[3]、斯格明子(Skyrmion)[4]和扭结[5]等,在凝聚态物理以及高能物理等领域具有广泛应用。目前旋量BEC 中的自旋织构主要通过非均匀磁场中的自旋旋转产生,Leanhardt 等[6]在钠原子BEC 中通过磁场翻转的方式制备了无核涡旋结构,Choi 等[7]通过扫描磁场零点在光阱囚禁的钠原子BEC 中获得了斯格明子。然而磁场的构型较为单一且不易调节,不利于自旋织构的灵活调控。与磁场相比,相干光场的操控手段更加丰富,其中拉盖尔-高斯(Laguerre-Gaussian,LG)光因其独特的光强分布及携带轨道角动量的特性而普遍用于原子系综的光学相干操控[8]。2009 年,Leslie 等[9]率先利用LG 模式的拉曼光脉冲在自由飞行的铷原子BEC 中获得了斯格明子,但并未详细分析其动态形成过程。
本文主要通过数值求解含时薛定谔方程研究了斯格明子的动态形成过程,观察拉盖尔-高斯模式拉曼光脉冲作用下原子团各内态布居数的演化行为,通过选取合适的双光子失谐量和脉冲时间,在初态处于铁磁相或极化相时分别模拟了文献[9]、[7]实验观测到的斯格明子结构。其次,因实验中拉曼光通常经由复杂的光学系统聚焦到真空腔中的原子团上,而在研究中发现,若要通过LG 光获取斯格明子结构,则光斑与原子团两者尺寸应可比拟,此时精确标定原子团处的光斑束腰对于实验参数的选择和结果的分析十分关键,本文提出了一种通过拉曼过程中双光子拉比频率与空间位置的关系标定光斑尺寸的方法,讨论了失谐量与二阶塞曼效应的影响,为后期实验提供了参考。
1 F =1 三能级系统拉曼过程的理论描述
以文献[9]的实验为基础进行计算,在他们的实验中,拉曼光在BEC 形成9 ms 后作用于原子团[10],此时原子团充分膨胀,密度降低,原子间相互作用效应很弱,可以在一定程度上忽略[11]。故只考虑总自旋F=1 的无相互作用原子团在模式的LG 光作用下的双光子拉曼跃迁,示意图如Fig.1 所示,δ 为双光子失谐量,LG 光光场分布为其中为拉盖尔多项式,w为光斑束腰,e-ilφ表示携带的轨道角动量为

图1 (a) LG 光束与原子相互作用;(b)原子能级跃迁(ħωz 为|-1〉和|0〉之间的能级差)Fig.1 (a)Schematic diagram of LG beams interacting with atom cloud;(b)Schematic diagram of atomic transitions(ħωz is the energy gap between|-1〉and|0〉)
三能级原子在拉曼光作用下的哈密顿量(取ħ=1)为

式中HZ为系统的塞曼频移,Haf为原子与拉曼光相互作用引入的哈密顿量,为双光子拉比频率[其中Ωi(r)=μiEi(r)为单光子拉比频率],μi为跃迁偶极矩,Δ 为单光子失谐量,ω 为两束光的频率差,Fy代表自旋算符。
考虑光与原子近共振情况,即光的能量差与能级之间的能量差对应,首先对(1)式利用旋转波近似,并绝热消去可得到

式中ε 为二阶塞曼频移。将其哈密顿量代入含时薛定谔方程,得到本征矢系数含时演化方程组[12,13]

由于失谐量与二阶塞曼频移的影响,上述方程无法得到解析解,这里采用四阶龙格-库塔方法[14]对其进行数值求解,在下面的计算过程中,选取峰值拉比频率Ωmax作为频率单位,1/Ωmax作为时间单位。
2 计算结果与讨论
2.1 斯格明子制备条件的数值分析
考虑光场的空间分布,可知双光子拉比频率随原子团空间位置变化,通过控制光脉冲时间可以得到原子内态布居的特定空间分布,即自旋织构。在F=1 原子凝聚体中,对于初态分别处于铁磁相与极化相的自旋织构,波函数与弯曲角(Bending angle)的对应关系可表示为[15]
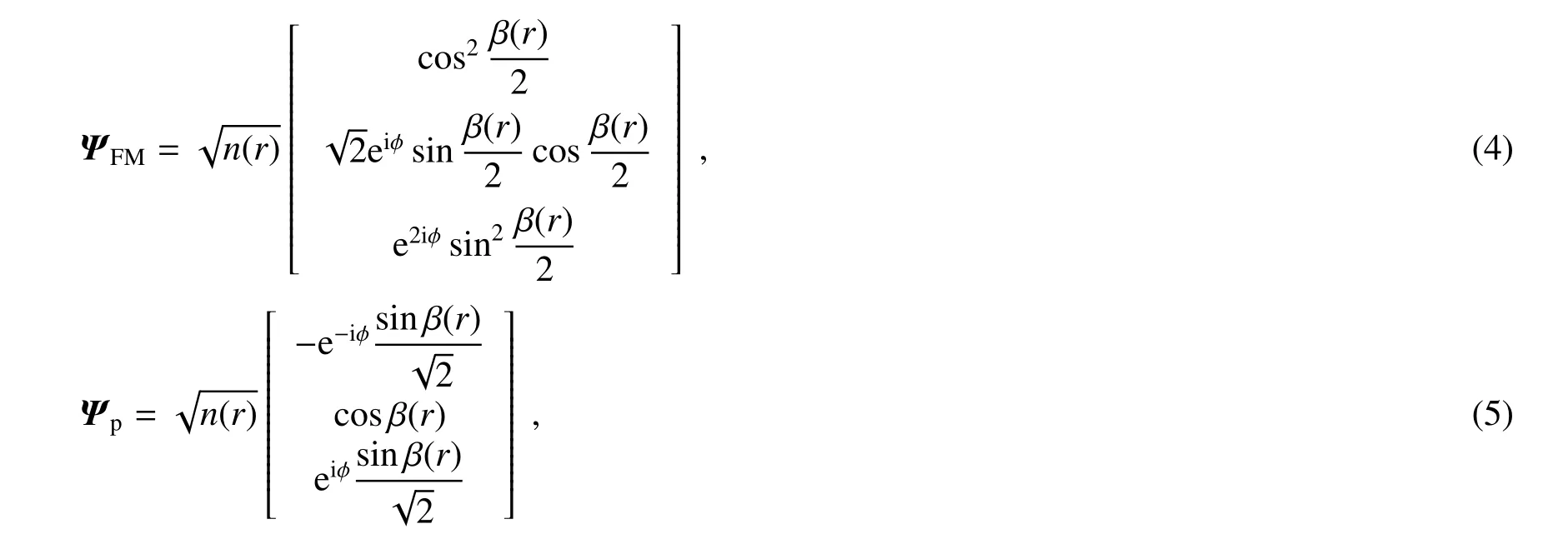
式中n(r)为原子团的密度分布,FM 代表铁磁相,P 代表极化相,弯曲角β(r)用于描述自旋在原子云上的旋转,局域自旋由矢量I(r,φ) = cos β(r)ez+sin β(r)(cos φex+sin φey)表示。在这种对应关系中,从原子团中心变化到边缘的过程中,β(r)从0 连续变化到π[16]。考虑原子团与一对同向传播的拉盖尔-高斯光束高斯光相互作用,首先将初态设定为|-1〉,即铁磁相,参照相关实验参数,光斑束腰设为90 μm,原子团直径设为40 μm,利用LG 光的峰值光强计算出此时的峰值拉比频率Ω1,调节光脉冲时间为7/(10Ω1)以及失谐量为0.178Ω1,可以得到如Fig.2(a)所示的结果,根据β(r)的变化情况容易看出所获得的自旋织构满足斯格明子的要求,其中R为三倍原子团半径大小,r为距原子团中心的位置坐标。受到Choi 等[7]利用调节磁场零点的方式得到斯格明子的启发,希望利用双光子拉曼过程重现该结果,将初态定为|0〉,即极化相,在一定范围内调节光斑束腰、失谐量与脉冲时间,观察自旋织构的演化,最终在光斑束腰定为60 μm、原子团直径定为40 μm、失谐量为0、时间为1/(2Ω2)时,定性得到了符合稳定的二维斯格明子的原子团径向分布图样,如Fig.2(b)所示,验证了此方法的可行性,其中Ω2为光斑束腰为60 μm时的峰值拉比频率。
2.2 利用布居数振荡标定光斑束腰
在利用高斯光束驱动拉曼过程实现自旋-轨道耦合等实验中,光斑束腰通常远大于原子团直径,原子近似感受到均匀光场的作用,通过调节失谐量与二阶塞曼频移,原子团整体布居数呈现规律的振荡行为,可以用其振荡频率来标定拉曼耦合强度[17]。由前面的数值分析可知,为获取特定的自旋织构,光斑大小应与原子团大小可比拟。此时,拉曼光光强的空间分布会导致各态上粒子数布居的振荡行为更加复杂。同样在三能级系统中对此进行了数值模拟,将原子初始态制备到|-1〉上,选取与模式的拉盖尔-高斯光束,其束腰为30μm,考虑原子团直径为10μm,计算了原子团各态布居数的时间演化,结果如Fig.3(a)~(c)所示,横坐标为振荡时间,纵坐标为各能级粒子布居数比例,由于原子团不同空间位置的振荡频率不同,整体粒子数布居表现为多种频率振荡的叠加,没有具体的规律性可循。
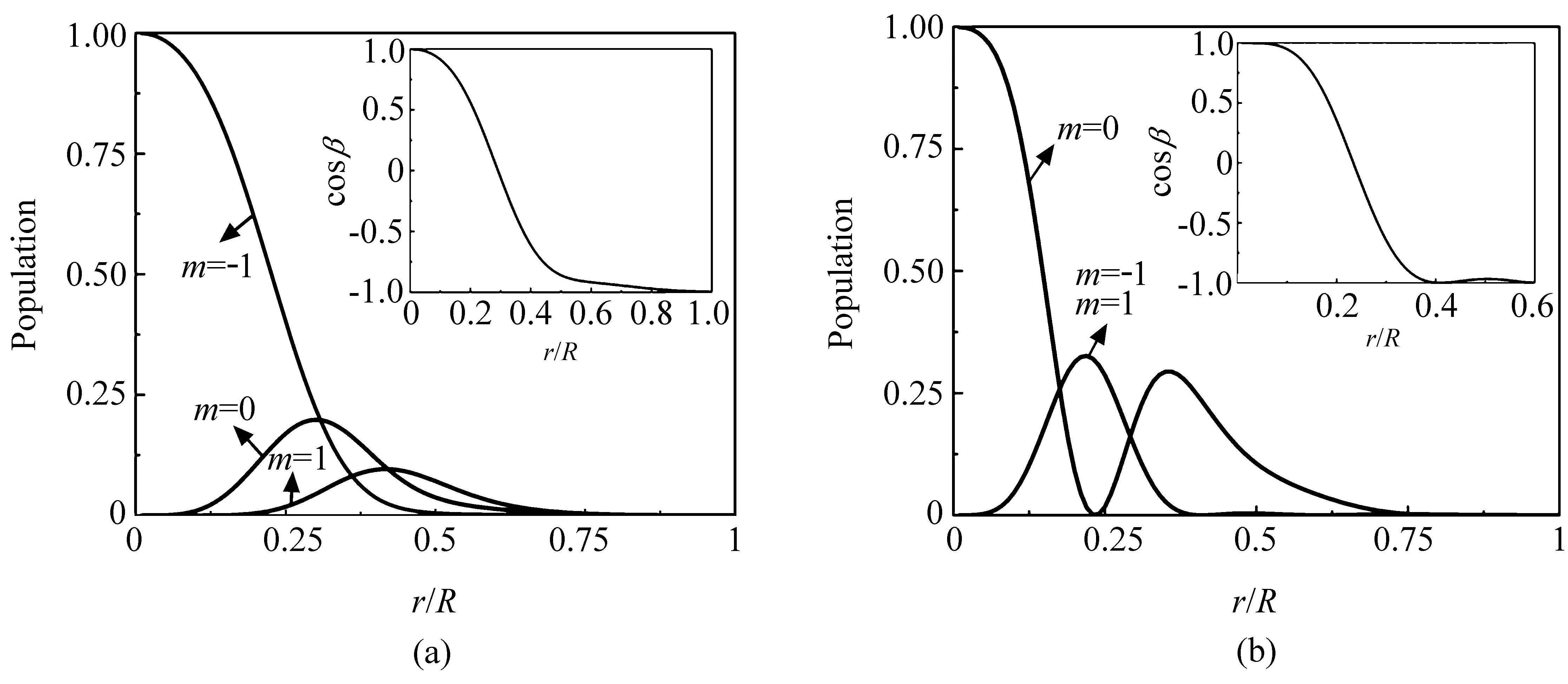
图2 斯格明子占据数在(a)铁磁相和(b)极化相下的分布Fig.2 Population[inset: cos β(r)]of Skyrmion from(a)FM phase and(b)polar phase

图3 各能级占据数无规分布:(a)m=-1;(b)m=0;(c)m=1;占据数随时间的演化:(d)r =2.5;(e)r =7.5Fig.3 Irregular oscillation of population:(a)m=-1;(b)m=0;(c)m=1;Population change with time:(d)r =2.5 μm;(e)r =7.5 μm
在实际的实验过程中,拉曼光通常经由复杂的光学系统聚焦到真空腔中的原子团上,在原子团处实际束腰与理论数值一般不一致,准确测定原子团处的光斑束腰对于实验参数的选择和结果的分析十分关键。通过上述计算得到,分别对应r= 2.5 μm、r= 7.5 μm 空间位置的粒子数随时间的变化如Fig.3(d)、(e)所示,发现原子团空间各点处粒子数布居近似按照正弦振荡,且振荡频率取决于各点处的光强,故分开研究单点的原子振荡性质,通过单点原子的振荡频率与光强的对应关系反推光斑束腰大小。
若忽略双光子失谐量与二阶塞曼频移影响,通过本征矢系数含时演化方程组可以解析求得mF= 0态的布居数振荡:将不同空间位置|0〉态原子的振荡频率用正弦函数拟合,根据光斑束腰进行拟合。Fig.4(a)、(b)是在设定束腰为30 μm 的情况下考虑不同的二阶塞曼频移得到的振荡频率与光强的拟合曲线,随着失谐量与二阶塞曼效应的增大,拟合得到的光强与实际数值的偏差也逐渐变大。但由于LG 光中心光强较低,二阶塞曼频移与失谐量的影响更加明显,因此中心拟合的光强偏差更远。分别在0~2 kHz 的范围内调节失谐量与二阶塞曼频移时,通过计算拟合得到的光斑束腰大小以及对应的相关系数R2变化的图像如Fig.4(c)、(d)所示,随着失谐量或二阶塞曼效应的增大拟合结果误差增大,在失谐量和二阶塞曼效应超出1 kHz 后,相关系数R2下降较快,故此方式适合在失谐量与二阶塞曼效应较小的情况下使用。

图4 光强随(a)失谐量和(b)二阶塞曼频移的变化;束腰随(c)失谐量和(d)二阶塞曼频移的变化Fig.4 Intensity change with(a)detuning and(b)second-order Zeeman shift;Waist change with(c)detuning and(d)second-order Zeeman shift
3 结 论
通过求解含时薛定谔方程研究了LG 光驱动F=1 三能级系统拉曼跃迁制备特定的自旋织构。在初态处于铁磁相时通过调节失谐量、光脉冲时间以及光斑束腰,数值模拟验证了Leslie 等获得的斯格明子结构,而后将该方法推广到初态处于极化相的情况,同样获得了与Choi 等利用磁场操控自旋旋转方法得到的实验结果相符的斯格明子结构。并研究了原子团不同空间位置的双光子拉比频率与光强空间分布的关系,据此提出了一种精确标定原子团处光斑束腰的方法,为自旋织构的实验制备提供了参考。

