自适应阶次分析在风电机组齿轮箱故障诊断中的应用

聂金生，郑 涛，林逸峰

（1.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122；2.浙江华东测绘与工程安全技术有限公司，浙江 杭州 310014；3.浙江中自庆安新能源技术有限公司，浙江 杭州 310018）

0 引 言

随着煤炭、石油等能源的逐渐减少，人类越来越重视可再生能源的利用。风力发电是可再生能源中最廉价、最有希望的能源，而且是一种不污染环境的“绿色能源”。碳达峰、碳中和关乎中华民族永续发展和构建人类命运共同体，而且碳达峰、碳中和是一场广泛而深刻的经济社会系统性革命。由于大部分风场所在环境的特殊性，即地处山区、海边、戈壁等，季节和昼夜温差大、风沙问题严重、污染等级高，加之风电机组自身具有低速、变载、零部件众多、传动系统复杂、分散部署、距离远、运行方位高以及人工实施维护困难等特点，导致传统的事后维修和周期性检修模式代价高昂，而离线点检模式耗费的人力成本又非常巨大，因此需对风力发电机组开展在线监测。齿轮箱是风力发电机组的关键部位，目前国内外齿轮箱种类多、质量参差不齐，风机运行过程中若对早期故障和隐患不能及时判断和预警，遇到齿轮箱齿轮不对中、齿轮箱齿轮啮合不良以及齿轮箱轴承磨损等情况时将会导致风机强制性停机，影响风机发电，从而造成重大损失，因此通过精确地数据采集分析来监测齿轮箱变得尤为重要。

在变转速转子故障诊断方面，唐贵基等人提出一种基于SSD-HT时频阶比跟踪的转子故障诊断方法[1]；杨炯明等人在阶比分析中引入瞬时频率理论，研制出了虚拟式旋转机械特征分析仪[2]；解武波等人提出一种基于局部均值分解和Fisher判别的风机机组齿轮箱故障诊断方法[3]；BORGHESANI P等人提出了一种新的基于速度同步的离散傅里叶变换，提高了计算阶次跟踪的分析效果[4]；WU J D等人基于递推最小二乘滤波的阶次跟踪算法对振动信号和声发射信号进行了特性分析和实验比较[5]；PAN M等人提出了一种可调谐加权因子，用于有效地区分和分离旋转机械测量信号的闭合和交叉阶分量[6,7]；WANG K S等人采用多种阶次跟踪技术对变速谐波振动去噪，强调包含裂纹信息的非阶数相关振动，论证了阶比跟踪技术在转子裂纹检测中的优越性[8]；WU J D等人通过自适应阶次跟踪技术提取阶次特征作为神经网络的输入，提出了利用网络开发故障诊断系统的人工神经网络技术[9]；张程鹏等人通过Compact RIO阶次跟踪和信号包络提取技术相结合的方法，分析了风力发电机组齿轮箱变速过程中振动信号非平稳的特点[10]。在滚动轴承和齿轮箱的故障诊断方面，通过阶次分析有效识别和提取变转速工况下的非平稳特征信号，有效识别出非常接近且微弱的振动特征成分，从而成功地检测出不同类型的齿轮故障。

从以上的研究现状来看，故障诊断技术只经历了短短几十年的发展，但已经在风电机组轴承、齿轮箱以及发电机等的监测诊断得到了长足发展和广泛应用。由于风力发电机组长时间不间停运行，风速不受控，传动系统紧密相连，高速轴、低速轴之间不断啮合、集中受力，风电机组传动系统的部件长期处于摩擦、冲击、振动或腐蚀等自然损耗状态，一旦出现故障，就会影响风电机组的稳定性和发电量，甚至会导致风机强制停机。

近年来，风机齿轮箱在线监测和故障诊断技术得到了快速发展，基于广义共振和共振解调的故障诊断技术在旋转部件故障诊断中得到广泛应用，但是这些工作通常会预设一个二次或多次的风机齿轮箱转动模式。由于齿轮箱旋转速度会随着时间变化，风机运行时齿轮箱的旋转角速度会改变，因此特征频率和故障频率也会随之改变，若依旧用同一周期对信号进行采样，只能采集到该故障频率为根据转速而定的范围。在噪声与信号能量分散的作用下，该信号频率强度会降低且信号会产生模糊，无法得到一个准确的故障频率值。

针对此漏洞，根据齿轮箱开始启动、加速、匀速、减速以及刹车等启停特点，基于阶比跟踪技术对该风电场传动系统的齿轮箱进行了振动监测。采集某一时间段内的运行数据，通过最小二乘法拟合出齿轮角度增量和时间增量之间的关系，引入振动信号，通过传统的快速傅里叶变换（Fast Fourier Transformation，FFT）和阶次分析方法，得到等时间步长和等角度步长的频谱图并对其进行对比分析，有效解决了齿轮箱变速转动过程中振动故障信号采样模糊的问题。该技术可以精准判断风电机组齿轮箱振动故障，是一种可靠的风电机组发电运行过程中监测齿轮箱故障的方法。

1 基本理论

1.1 阶次分析

阶次跟踪技术（Computed Order Tracking，COT）是处理旋转机械非平稳振动信号的重要技术之一。对于变转速的旋转机械设备，包括发电机轴承、齿轮箱轴承等的故障诊断。相对于参考轴或键相信号进行等角度增量采样时，虽然此信号在时域上是非稳定信号，但是在角域上却是稳定信号。对角域上的稳定信号进行谱分析便可得到清晰的图谱，即阶比谱。振动信号表示为：

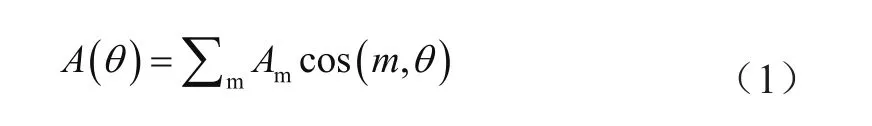
式中，A(θ)表示转过角度为的振动信号的幅值，Am为阶次为m的谐波分量的幅值（m=1,2,3,…）。

阶次、频率、转速之间的关系为：

式中，m为振动信号的阶次，f为观测对象的频率，n为参考轴的转速（单位：rpm）。

风电机组运行过程中，齿轮箱的角度增量为：

式中，θ(t)表示t时刻的角度增量，L(t)为t时刻齿轮的旋转线位移，r为齿轮的半径。

岳晓峰等人在变速箱故障诊断中应用阶次分析时，假设变速箱转轴的运动模式为匀加速运动[11]。而实际工程中，转轴的运动往往较复杂，因此考虑了更复杂的匀变加速运动。将齿轮箱的角位移表示为：

式中，a1、a2、a3、b1、b2、b3、c1、c2以及d1均为常数。

在时域信号中，设键相脉冲的角度增量为Δθ，任意4个相邻的时刻t1、t2、t3以及t4，将其代入式（4）中构成数据矩阵为：

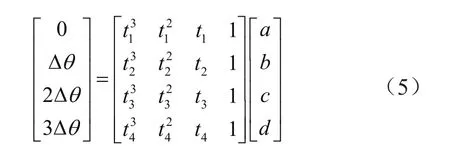
求得a、b、c以及d的值，回代到式（4）即可求得Δθ和t的关系。

1.2 采样插值和拟合

采样时间的间隔决定了采样的精度，由于实际采集数据过程中，采样结果为离散的点，为提高计算精度，更接近实际振动，常采用插值的方式实现离散函数逼近，以满足给定约束。与采样时间间隔的精度一样，插值方法的精度同样决定了重采样的幅值精度。

假设在齿轮某一部位布置键相标记k，对以上采集的数据进行等角度重采样，采样时其角度增量Δθk为2π的整数倍，即：

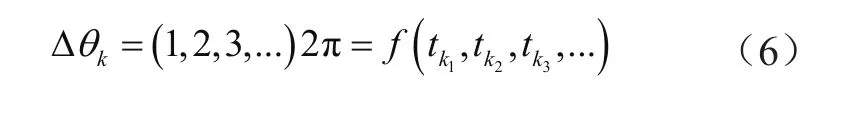
通过最小二乘法拟合出Δθk与tk的关系，在[iΔθ,(i+1)Δθ]之间进行等角度细化，即等角度采样的键相序列为θk，km=1,2,3,…,M（M为阶次分析的信号长度，即单次分析的采样点数）。

以匀变加速度为例，假设原始信号为：

A为常数则通过最小二乘法对θ′与t的关系分别进行二次和三次多项式拟合，并进行阶次分析，得到如图1所示的关系。

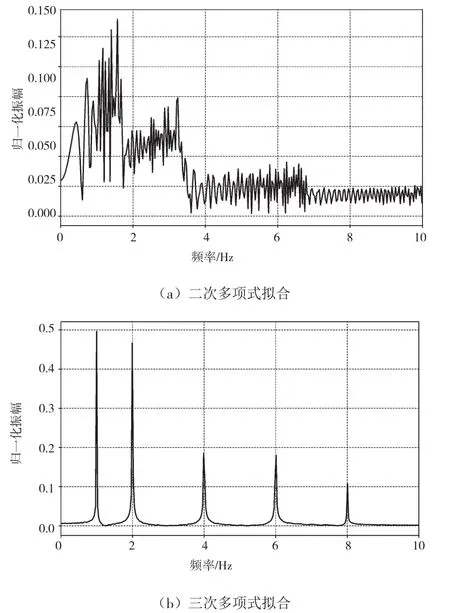
图1 不同拟合关系对阶次分析的影响

从以上不同拟合关系得到的阶次分析结果可以看出，相较于二次多项式拟合，三次多项式拟合由于和原始信号阶次相同，以该方式拟合后的阶次分析更清晰地呈现出振动频率，具有更好的阶次分析效果和更高的分析精度。

为提高拟合的近似度，可以采用线性插值的方法对采样的角度间隔进行细化。对式（7）进行线性插值后，分析得到的阶比谱将存在一定底噪。由于插值方法的阶次分析信号无法完美重现原本的信号，存在一定的噪声，该噪声所具有的频带宽度远远大于它所作用系统的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，因此将其当作白噪声进行处理。

对式（7）中的信号分别进行等时间采样和等角度采样，0～5 s和59～60 s内两种采样方式的对比结果如图2所示。从图2（a）可以看出，0～5 s的时间段内，由于转速较小，等时间步长采样的结果优于等角度采样，拟合的曲线更接近于原始信号。随着加速度的不断变化，转速随之不断发生变化。在59～60 s，等角度采样的精度明显优于等时间采样。因此，对于变转速的运动，采用等角度采样能得到更接近于实际振动的信号。

阶次分析与FFT变换的区别在于分析域不同，阶次分析将FFT变换的等时间采样转换为等角度重采样。对原始振动信号在角度域上重采样，大幅提高了分析频率的精度，以及在后续分析中的准确性。随着时间的变化，角度键相的稀疏程度发生变化，对比图2（a）和2（b）析，加速度为正时，随着速度不断增加，等时间间隔（蓝色数据点）内的，角度键相（绿色数据点）分布变得稠密；反之，分布稀疏。

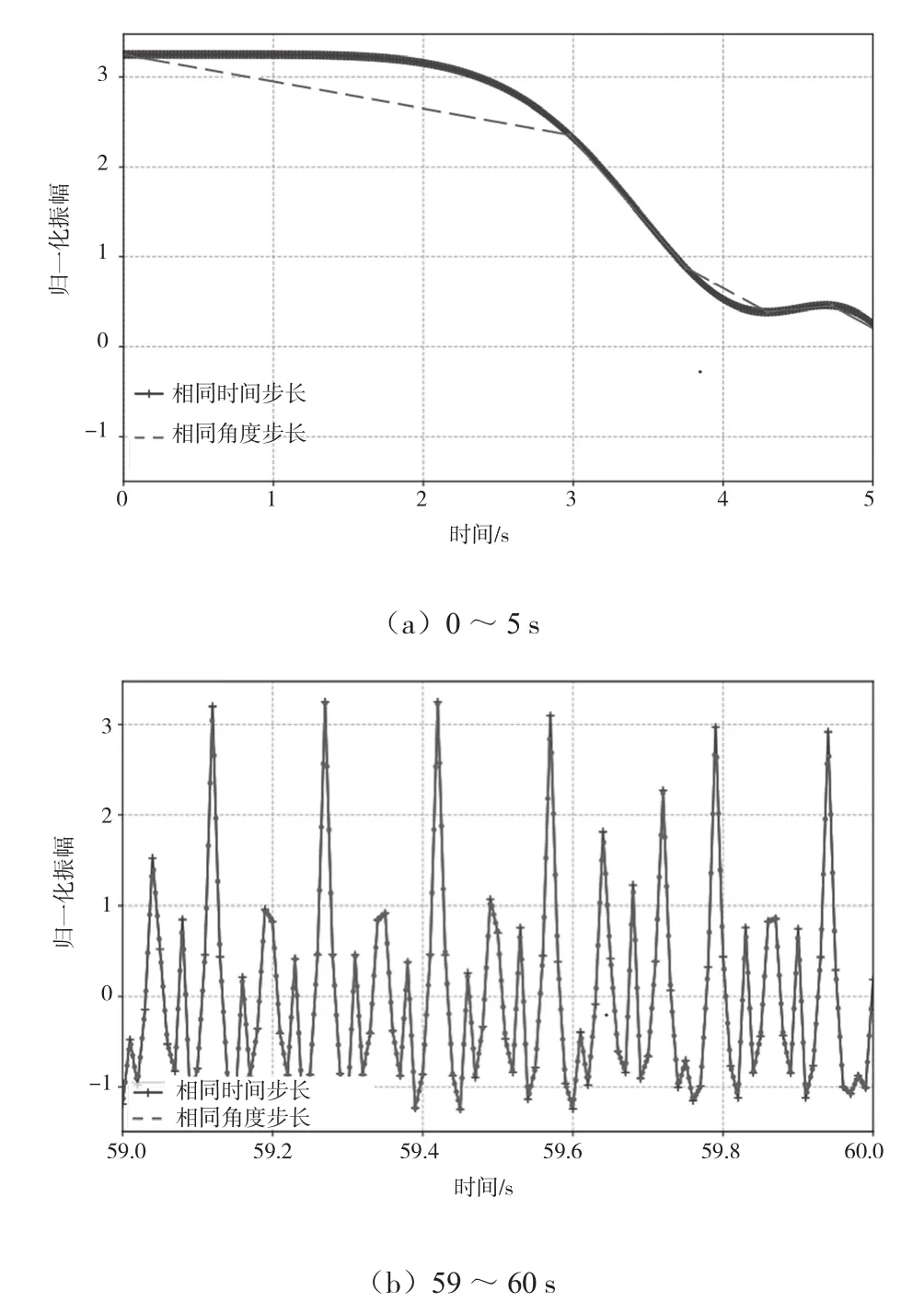
图2 等时间步长和等角度步长采样对比图

2 数据采集和分析

2.1 运行数据实地测量

以某国营风电场在运行2 MW风机机组为例，实际运行时，CMS系统会对风电机组运行时各部件的信号进行分析，此处以齿轮箱输出轴前轴承的振动幅值信号为研究对象。在风机齿轮箱运转的某一时间段内进行等时间采样，采样频率为100 Hz。风机运行过程中齿轮箱加速度随时间的变化如图3所示。

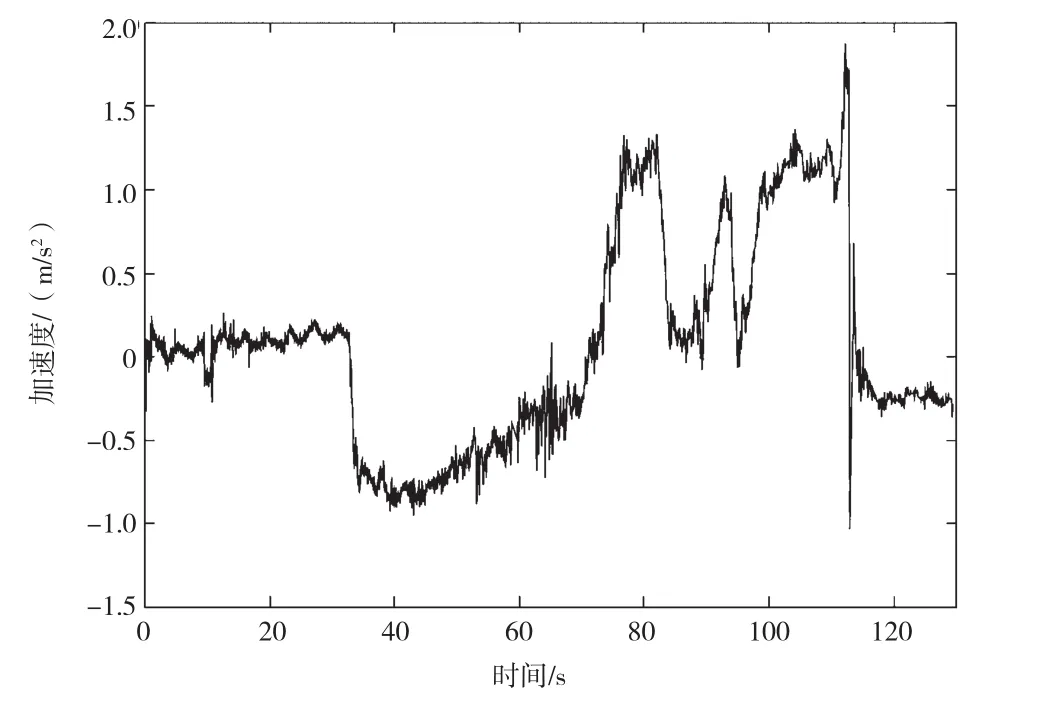
图3 风电机组齿轮箱运转过程中加速度与时间的关系

从图3可以看出，风机齿轮在运转过程中，加速度时刻都在发生变化。0～30 s内，加速度值近似为0，可以看作匀速运动；35～60 s和60～80 s内又可以看成加速度增量不同的两段匀变加速运动。为使分析结果更接近实际工况，通过对已有测量数据插值的方式，重新构建等角度间隔的数据集。引入仿真振动信号模型参数如表1所示。

表1 振动信号模型参数

2.2 运行模式的自适应

图3描述了一个典型的风机从匀速稳定运行、刹车、再启动到匀速稳定运行的过程，本研究在该运动过程中附加了表1提供的振动信号模型参数，对此分别进行时间FFT和阶次分析，得到如图4所示的频谱图。

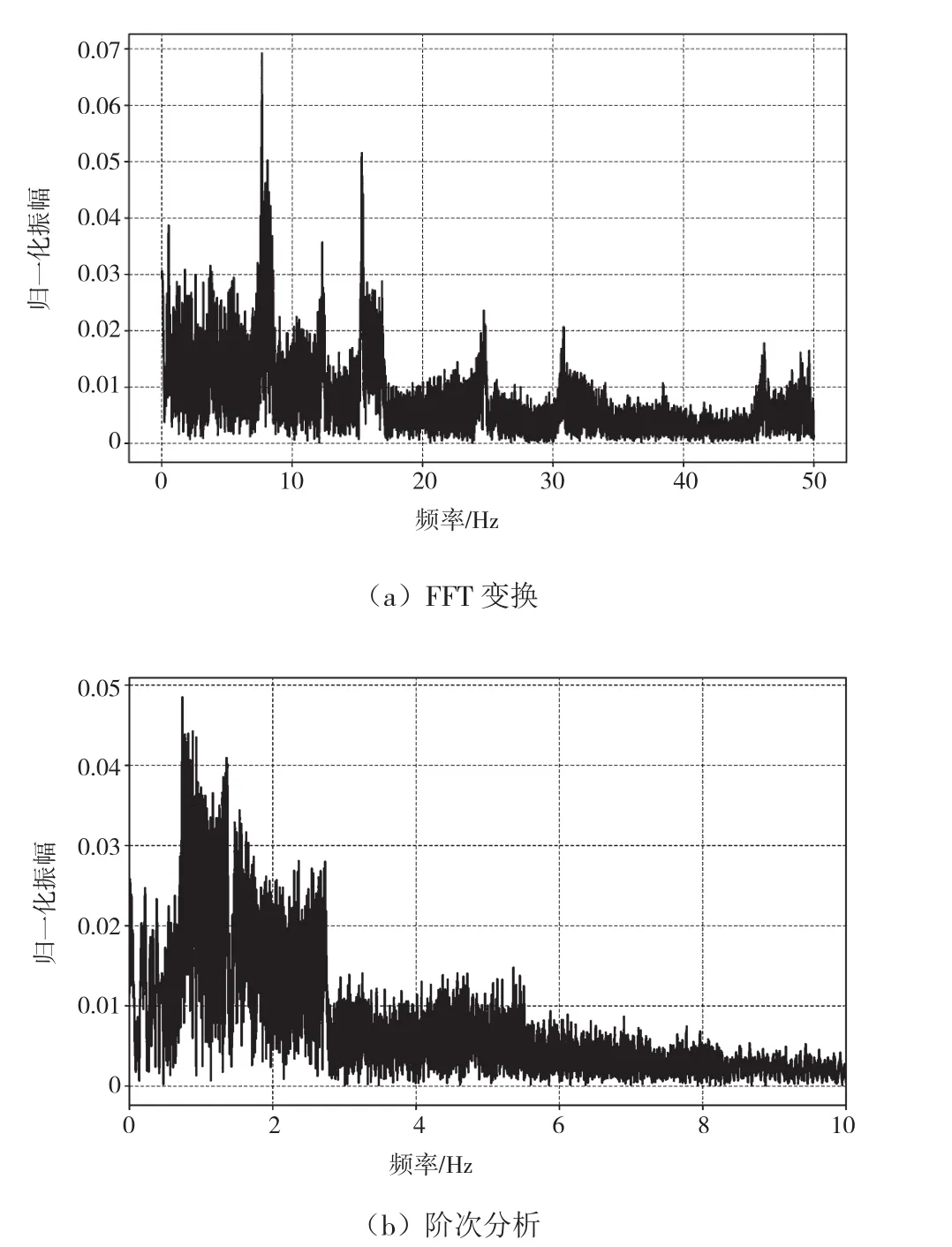
图4 等时间步长频谱图

图4（a）中频率成分繁复杂乱，由于振动信号的频率是随着时间不断变化的，属于非稳定信号，而FFT变换单一的通过改变窗函数的大小和形状进行分析，很难适应随时变化的信号，故得到的谱线反映的是窗内的所有频率成分，无法识别故障频率的特征。为更好地接近原始信号，用三次多项式进行拟合，并进行阶次分析得到图4（b）所示的阶次分析频谱图。从最终结果看，对等时间采样的信号，采用阶次分析得到的阶比谱中频率模糊，依然不能清晰呈现故障特征。

通过等角度重采样和等角度键相间线性插值，得到重采样信号并进行阶次分析，得到如图5所示的阶次频谱图。从图5中可以清晰地看到阶次分别为1、2、4、6以及8的谐波成分，与仿真的振动信号的频率成分相吻合。对于变转速运行的复杂工况，阶次分析有效避免了等时间采样导致的采样模糊、故障频率的频率范围模糊且信号强度低等问题。

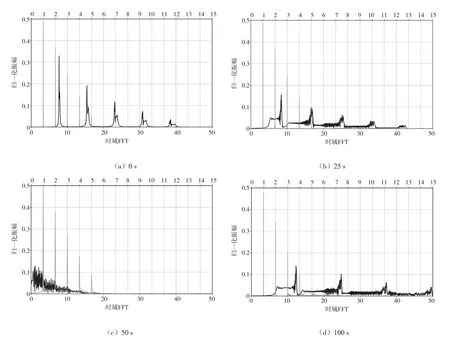
图5 不同时刻基于时域的频谱分析和阶次分析结果

3 结 论

风电机组运行过程中，齿轮会经历启停且运转速度变化频繁。在高速旋转并受到集中力的情况下，基于等时间采样的振动信号的能量将会分布于与齿轮箱转速相关的范围内，即故障频率将分散于某一频域范围，不能精确得到故障频率和确定故障原因。当采用阶次跟踪技术时，通过等角度采样的方式自适应调整采样频率，将时域上的非稳定信号转化为角域上的稳定信号，通过阶次分析得到的阶比谱可以清晰地看出阶次谐波成分，从而精确识别故障频率。

常见的阶次分析技术需要预先假设一个二次或者多次的关系对设备运行规律进行拟合，一旦设备的运行规律较为复杂，则难以准确进行阶次跟踪。使用自适应阶次分析技术可以适应设备各种负责的运行模式，在风电机组齿轮箱以及其他类似设备的实际运用中可以更好地捕捉到设备和故障的特征，使得阶次分析技术在轨交故障诊断的实际应用中具有更广阔的应用前景。