基于蒙特卡罗仿真的全自动运行系统弹性评估方法研究
郭子薇,燕 飞
(北京交通大学电子信息工程学院,北京 100044)
随着中国城轨的高速发展,全自动运行系统(Fully Automatic Operation,FAO)以其安全、高效的特点引发了新的发展需求。当前,北京、上海等城市日均客流已超千万,运营负荷巨大,安全运营面临严峻挑战,采用全自动运行技术是有效解决途径和必然选择[1]。
弹性的概念经Holling[2]引入生态领域后,经过几十年的发展,弹性研究已扩展到组织管理、经济、基础设施建设以及电网等诸多领域,以评估目标系统对威胁其正常运行的中断作出的反应能力。为进一步提升全自动运行系统抵抗扰动以及从非正常态中快速恢复的能力,研究人员必须能够定量评估在不同的设计或维护管理方案下系统的弹性水平,以便做出最佳决策。因此,提出围绕全自动运行系统的弹性评估方法是对全自动运行系统的弹性工程实践的基础环节,同时对弹性在工程领域的应用也起到了重要作用。目前,弹性的度量方法并没有标准化,弹性度量仍是一个具有挑战的问题,从弹性的定义出发,目前已有的系统弹性度量通常围绕系统性能降级程度与快速恢复性展开,一般可分为确定型度量和概率型度量两类[3]。
确定型度量主要是对系统在某次确定的扰动情形下从性能降级到性能恢复这个过程的弹性定量评估,由于系统所经受的扰动、产生的性能降级和恢复时间都具有随机性,基于单次扰动下的系统弹性能力的确定型度量方式本身具备了随机性,因此较多的研究人员开始研究概率型系统弹性能力度量方式。Jin等[3]对道路运输网络的各条线路受扰动情况以及降级水平都以概率的形式给出,以故障后与故障前的网络最大数据流的比值作为弹性度量值,经过多次的随机抽样,统计出了系统的平均弹性水平。
以北京全自动运行线路燕房线为例,采用蒙特卡罗仿真方法模拟系统受扰动以及性能下降的随机性,以故障前后系统数据流权值的损失比量化系统性能下降水平,经过多次仿真统计出系统的平均弹性水平,为全自动运行系统的弹性评估提供一种更为可靠、能规避扰动随机性问题的概率型弹性评估方法。
1 弹性计算方法
弹性通常被定义为系统抵御扰动并快速恢复的能力,一般采用“弹性三角”曲线来表征系统性能的变化过程,同时将由于遭遇扰动导致曲线下降而缺失的面积比作为衡量系统弹性的指标。但对于全自动运行系统这样一个庞大而复杂的系统来说,很难将系统各设备故障前后的性能变化用曲线进行准确描述,因此采用Zobel[4]提出的基于几何数学模型的弹性度量方法,在已知故障导致的性能下降程度,以及故障恢复时间后,该方法假设故障以一个恒定的速度进行恢复,降低了弹性的量化难度。归一化剩余性能值以系统故障后和故障前的系统数据流权值的比值来衡量。
为了便于对全自动运行系统的弹性展开定量计算,做出以下假设。
1) 扰动:每次只考虑系统遭受一次扰动,每次扰动只影响系统的一个组成部分,中断发生在第i个设备的概率为qi;
2) 性能下降:设备的性能下降水平遵循离散分布(对于初始数据量为Di的设备i,其性能下降后的数据量可能降为Di,1,Di,2,…,Di,k,每个值对应的概率为pi,k);
3) 恢复:设备的恢复时间服从对数正态分布(对于设备i,其恢复时间为
假设1是为了简化研究的问题,同时也是弹性分析中常用的假设,假设2是对设备遭受扰动后的性能变化进行了状态抽象,降低了运算的难度,而假设 3将设备的恢复时间采用对数正态分布进行描述,是因为通过查阅相关文献[5-10]发现,对数正态分布式系统修复时间是最广泛使用的分布,且参考文献中有交通事故的持续时间服从对数正态分布的分析,因此,本文采取对数正态分布对设备的恢复时间进行描述。
Zobel[4]在其弹性度量方法中考虑到由于在系统设计过程中无法确定系统遭遇扰动后的性能变化过程,因此其假设系统在t0时刻遭遇扰动后,性能下降X,随后以恒定的恢复速率进行恢复,记恢复时间为T,如图1所示。T*是T的可能值集合中的严格上界,系统遭受的任何扰动行为均可在T*时间内恢复。可以看出,三角形的面积就是系统在某种特定扰动后的性能损失量,因此,用归一化的性能损失量表达弹性可用下列公式表示:

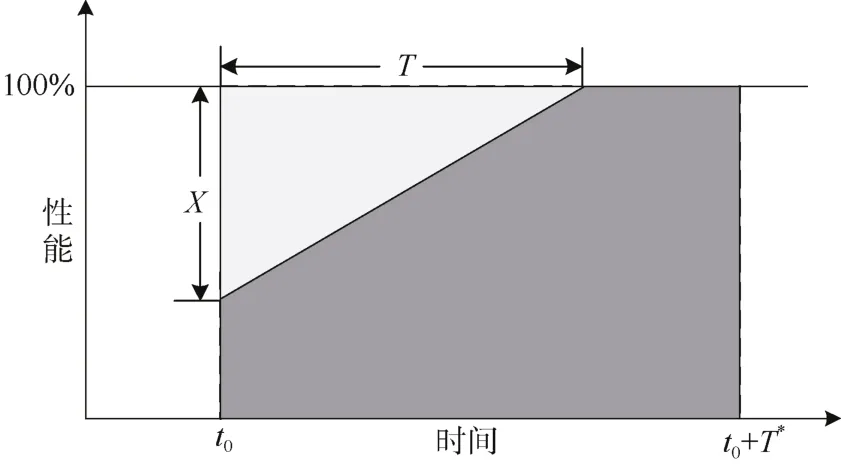
图1 基于恒定恢复速度的弹性度量Figure 1 Resilience measurement based on constant recovery speed
全自动运行系统设备组成较为复杂,找到统一的衡量各设备状态的指标较困难,同时也难以保证准确,因此用状态虚拟值来量化表示设备性能,设备的输出数据流的权值与状态虚拟值相同。设备正常工作时,状态虚拟值最大,当设备遭受扰动后虚拟值降低,统计设备间的数据流权值总和,用系统故障前后总的数据流权值的比值来表征系统性能的下降水平。因此考虑数据流权值的设备i的弹性可计算为:

考虑设备降级服从离散分布,恢复时间服从对数正态分布,因此,设备i的基于数据流权值的弹性期望可以计算为:
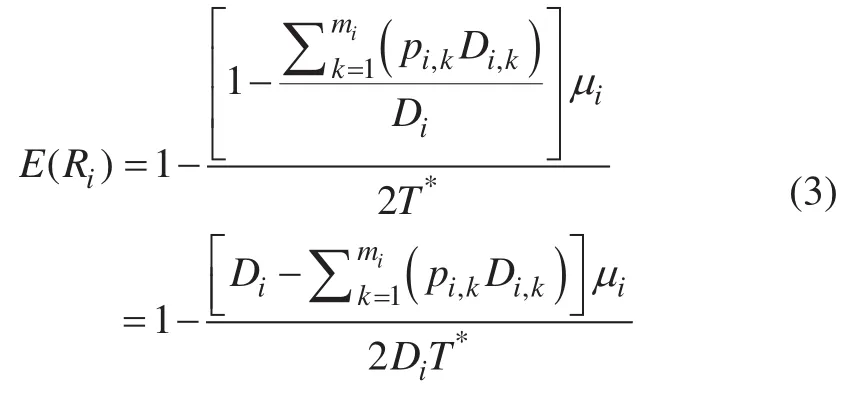
2 全自动运行系统参数确定
2.1 FAO系统原理及架构
全自动运行系统较传统的基于通信的列车控制系统(CBTC)具有更加完善的自动控制功能,以行车为核心,信号、车辆、综合监控、通信、站台门等多系统深度互联,信号系统与综合监控系统深度集成(行车综合自动化系统),提升了城市轨道交通运行系统的整体自动化水平。
全自动运行系统架构核心包括以下部分:
1) 控制中心核心设备:列车自动监控系统(ATS)、中心电力调度系统(SCADA)以及综合监控系统(ISCS)高度集成,形成行车综合自动化系统(TIAS),在运营组织方面,加强紧急情况处理,对信号、通信、综合监控等系统深度集成与整合,保证系统内部的协调工作。
2) 车站控制设备:以车站TIAS系统为核心,集成控制车站内与乘客乘降相关的设备,如乘客信息系统(PIS)等,响应中心命令,负责站内引导与应急处理。
3) 轨旁设备:包括列车自动防护系统(ATP)、联锁系统(CI)、辅助定位LEU系统等,可根据运营线路实际需要增加轨旁障碍物检测设备。
4) 车载设备:以车载列控系统(ATP/ATO)为核心,配备牵引制定、辅助测速等车辆设备,在车头加装视频监控设备(CCTV),增加车辆信息管理系统(TCMS),作为传输行车信息的专用系统。
为了降低计算量,将系统架构进行了适当的简化,如图 2所示,同时对重要的设备之间的交互关系进行了梳理。其中,箭头的方向表示数据流的信息传递方向。数据流的权值用输出该数据的设备状态虚拟值来表示。

图2 全自动运行系统架构Figure 2 Fully automatic operation system architecture
2.2 设备参数
全自动运行系统的各设备的故障模式较多,同时很难用单一的指标准确描述设备的性能,因此为了运算的统一与方便,根据设备故障后果严重程度不同进行性能降级等级划分。对每一等级设置“状态虚拟值”来定量表征设备性能,当设备正常工作时,该虚拟值最大,性能降级越严重,其虚拟值越低。
在城市轨道交通列控系统中,用SIL等级表示设备应达到的相应安全水平,SIL等级越高,说明该设备的正常运行对保障系统安全越重要。参考《城市轨道交通全自动运行系统运营需求导则》中对全自动运行系统各设备的SIL等级要求,SIL等级越高的设备,状态虚拟值设置越高,以此表示其设备故障对系统的安全影响越大。SIL4级的设备,未故障时状态虚拟值为8,下降性能共设3级,相对状态虚拟值依次降为4、2、0;SIL2级的设备正常工作时状态虚拟值为4,各性能降级等级对应状态虚拟值依次降为 2、1、0;对没有SIL等级要求的设备,均设置为正常运行时状态虚拟值为2,性能降级等级对应状态虚拟值依次为1、0.5、0。
采用上述设备状态虚拟值的设置规则,为图2全自动运行架构中所涉及的主要设备确定状态虚拟值。
调查了北京燕房线2017年12月到2020年10月的信号系统和综合监控系统的故障数据记录,对CI、ATO、ATP、ATS、ZC、ISCS、转辙机以及轨道电路这8种重要设备的故障数据进行了统计,对故障记录模糊的数据进行了剔除,其中发生在计算机联锁设备(CI)的故障共有 67条,发生在自动驾驶(ATO)子系统的故障共有59条,发生在自动防护(ATP)子系统的故障共有57条,发生在综合监控系统(ISCS)的故障记录共有367条,而自动监控系统(ATS)的故障记录最多,共有420条,转辙机和轨道电路分别为47条和19条,发生在区域控制器(ZC)子系统的故障记录相对较少,只有12条。由于燕房线开通时间较短,所统计到的故障数据有限,在之后的研究中,可以持续监测燕房线的故障数据,不断纠正研究结果。根据故障记录描述,统计了每条故障从发生到故障恢复的时间,对各设备对应的故障恢复时间进行了对数正态分布参数计算,同时统计了各设备的故障频率,将设备的故障频率作为设备故障的概率,另外根据设备不同,性能下降等级对应不同的状态虚拟值,以各性能等级出现的频率确定了各虚拟值对应的发生概率,具体数据见表1。
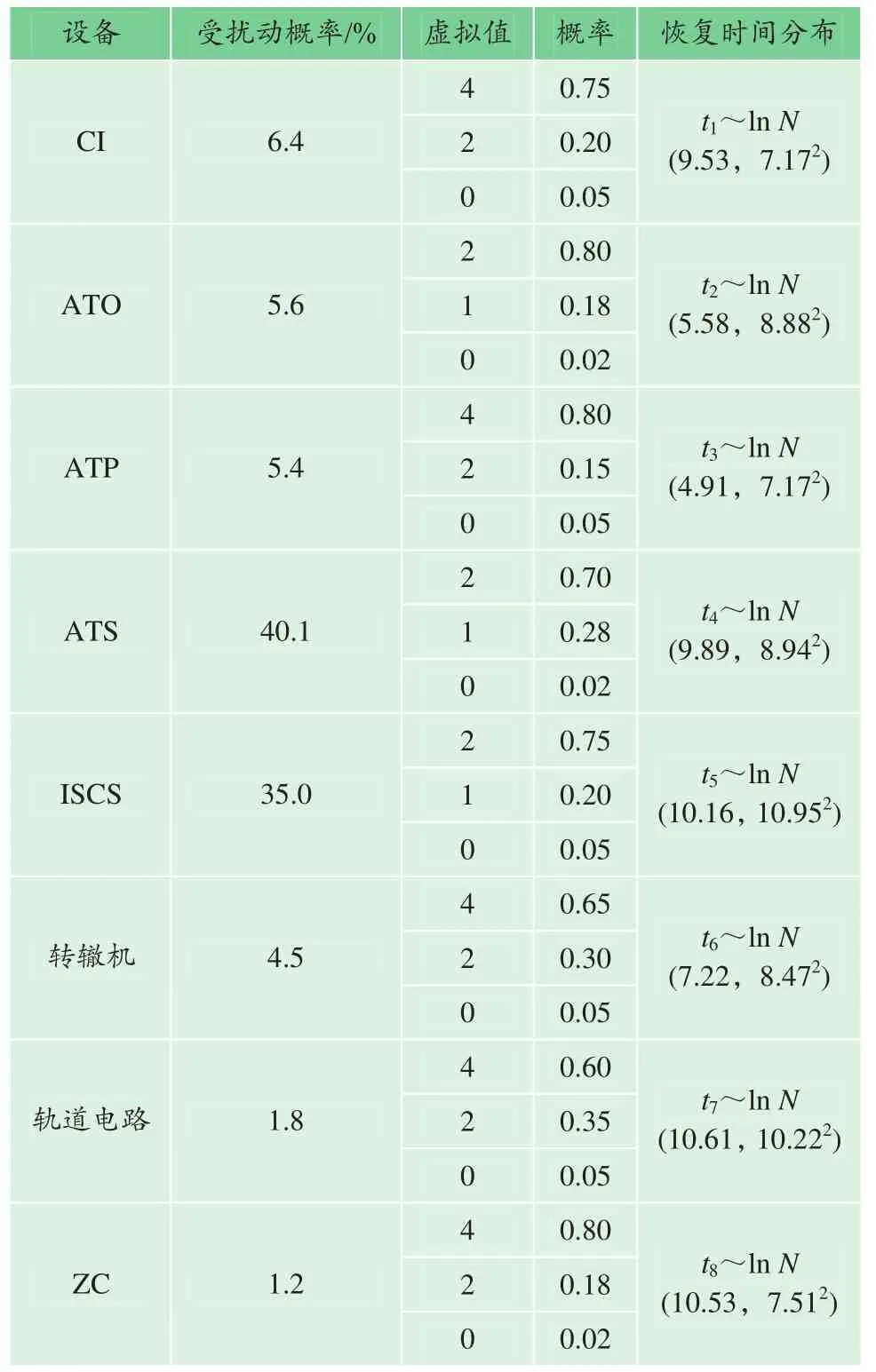
表1 设备相关参数Table 1 Device-related parameters
3 基于蒙特卡罗的系统弹性评估
蒙特卡罗方法是一种基于仿真统计的计算方法,其核心思想是建立系统中概率过程的仿真模型,然后使用多次试验的方法,计算得到系统特征。针对系统弹性这一指标,由于研究对象的复杂性,以及系统可能遭受的扰动、性能下降和恢复过程的随机性,蒙特卡罗仿真可以作为一种系统弹性评估的有效方法。
采取蒙特卡罗仿真方法来探究基于全自动运行系统状态虚拟值的系统弹性,模拟全自动运行系统设备故障、设备故障程度以及恢复时间点的随机性,通过105次仿真运算,统计出系统弹性的平均值,具体仿真步骤如下。
1) 将设备的输出数据流权值设置为该设备的状态虚拟值,计算基于全自动运行系统架构中各设备间的交互关系的数据流权值总和,各设备均正常工作,数据流权值取最大值Ds。
2) 根据各设备可能遭受扰动的概率qi,抽样确定受扰动的设备j。
3) 根据设备故障后性能下降和恢复时间所服从的分布,抽样确定设备j受扰动后系统下降信号值和恢复时间tj。
4) 在K次扰动下计算系统弹性
5) 考虑到扰动、性能下降和恢复时间的随机性,重复2)到4)步,直到迭代次数M。
根据燕房线2017年12月到2020年10月的信号及综合监控系统问题跟踪记录的故障数据,一共获取了ISCS、ATS、ATO等8个设备的故障统计数据,将这8个设备的故障数据进行系统的弹性计算,若能获得更详细更全面的设备故障数据,可扩展计算的范围。以图2全自动运行系统架构为基础,将各设备的输出数据流权值设置为对应的状态虚拟值,经计算,系统在正常运行时系统总的数据流权值为 182,设备故障的边界时间取24 h,采用Matlab进行蒙特卡罗仿真,得到 105次仿真的全自动运行系统弹性经验估计值:。该系统弹性的概率密度函数如图3所示,可以看到全自动运行系统弹性主要集中在0.98之后的区域,这表明在CI、ATP等论文中,讨论的8个主要信号系统设备中的大多数扰动系统表现的弹性都非常高,在某些特定的扰动下系统也可能体现出较低的弹性。
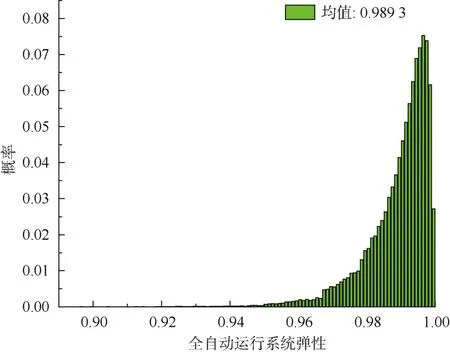
图3 全自动运行系统弹性的概率密度分布Figure 3 Probability density distribution of resilience in fully automatic operation system
图4给出了在CI、ATP等8类设备遭受扰动时全自动运行系统弹性的累积概率分布情况,在图中可以看到CI遭受扰动后系统的弹性跨度最大,系统的弹性可能会低于0.9,其次ATP和ZC遭受扰动后系统的弹性也可能出现较低值,这是由于 CI、ATP、ZC设备本身满足SIL4级,SIL4级设备的安全性对系统整体的性能影响很大,因此将SIL4级设备的各级性能状态值性设置较高;同时这几个设备在整个系统的拓扑结构中处于关键位置,与多个其他设备有交互关系,因此这3个设备故障后对系统整体的性能影响相对更大,也导致其弹性值会出现低值,因此在燕房线的日常运行中要重点关注CI、ATP以及ZC设备的故障情况,要从减少故障发生频率以及提升故障处理效率两方面进行改进。同时,从图中可以看到发生在转辙机和轨道电路的弹性概率累积分布跨度相对更窄,弹性值波动较小,且系统弹性值都在0.97以上,这说明转辙机和轨道电路故障时,系统的弹性受其影响较小,这是由于与转辙机和轨道电路有交互关系的设备只有CI,其发生故障后受其影响的邻接设备较少,因此其故障对系统整体的影响相对较低,所以当转辙机和轨道电路发生故障时,系统的弹性值相对波动较小,弹性值能保持在较高水平。另外,与其他设备相比,发生在轨道电路以及转辙机的故障处理过程相对及时,不用等待至夜间列车停运进行系统调试处理,而本文采用的弹性量化方法与故障的恢复时间密切相关,因此使得因转辙机和轨道电路故障得到的系统弹性能保持在较高值。
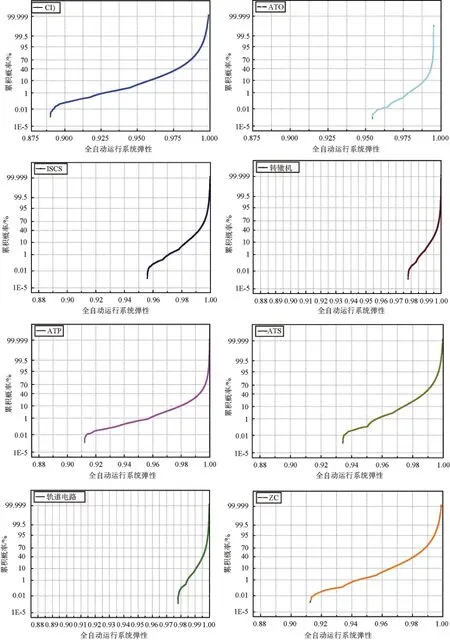
图4 不同设备遭受扰动下的全自动运行系统弹性Figure 4 Resilience of automatic operation system with different equipment disturbed
4 结论
通过对全自动运行线路燕房线过去 3年间的信号及综合监控系统故障跟踪记录表进行数据筛选,计算出CI、ATP、ATO、ISCS等8个设备的故障频率以及故障恢复时间分布函数,采用基于 Zobel的弹性量化方式以及蒙特卡罗仿真方法进行了系统弹性计算。
1) 通过105次蒙特卡罗仿真计算,求得了燕房线全自动运行系统的弹性估计值为0.989 3。
2) 分别计算了CI、ATP等8个设备遭受随机扰动时系统弹性值的概率累积分布,其中CI、ATP以及ZC在遭受扰动后系统的弹性值跨度较大,可能会出现较低值,因此在日常的列车运行过程中,应该加强对CI、ATP以及ZC设备的故障管理,尽量缩短其故障处理时间。
3) 转辙机以及轨道电路随机故障得到的系统弹性概率累积分布相对比较稳定,基本维持在较高水平,这与受转辙机和轨道电路故障影响的邻接设备较少有关,导致其故障后系统性能值下降相对较低,因此在计算系统弹性时,弹性值也不会出现较大的下滑。另外,由于处理转辙机与轨道电路故障无需等待列车停运再进行系统调试处理,节约了故障处理时间,这使得计算得到的弹性值也相对较高。
通过采取基于蒙特卡罗仿真方法对全自动运行系统弹性进行计算,将各设备受扰动以及性能下降程度都以概率的形式予以考虑,使弹性计算结果更能贴近系统真实的弹性水平,更能有效地反映系统整体的弹性情况,在实际的运营过程中,弹性计算量可作为综合反映系统受扰动后重新恢复正常的能力。目前,全自动运行系统的技术已趋于成熟,越来越多新修建的地铁也开始采用全自动运行系统,但围绕全自动运行系统的运营管理技术却还处于起步阶段,列车出现的紧急情况,调度人员只能在远程进行指导和处理,如何在列车出现紧急情况时,在没有司机的帮助下还能保证全自动运行系统的高效率,运营管理人员还需要更多的实际经验的摸索,而弹性作为衡量系统从不稳定状态恢复到正常状态的能力,可帮助运营管理人员在实际的运维操作中定量评估其应对措施效率的高低。
致谢:感谢城市轨道交通北京实验室项目资助。

