基于损伤分析的空心板桥荷载横向分布系数研究*

钱若霖， 苏佩， 杨谦

(1.陕西工业职业技术学院 土木工程学院， 陕西 咸阳 712000；2.中联西北工程设计研究院， 陕西 西安 710000)

装配式空心板桥预制方便，构造简单，受力明确，在公路和市政桥梁中应用广泛。但车辆的反复荷载和外界环境侵蚀使空心板桥的梁体和铰缝病害增加，这两种结构损伤会使梁体刚度和梁间传力有所削弱，进一步影响上部荷载在各片主梁上的分配。周颖针对小箱梁桥的裂缝参数外观特征，结合刚度模型分析数据，推导了静、动刚度折减系数，并通过静、动力状态下裂缝参数特征值与静、动刚度折减系数，分别回归得到了静、动刚度折减系数与对应裂缝参数之间的关系式，分析了静刚度与动刚度退化规律及两者间的关系；聂瑞锋等针对在役空心板桥，以关键参数为自变量、弯矩横向分布系数为因变量，采用多元非线形回归得出了弯矩横向分布系数计算公式，其中铰缝损伤程度采用铰缝失效长度与计算跨径的比值进行量化。该文沿用传统铰接板法理论基本假设，将空间问题转化为平面问题，考虑既有空心板桥服役期间梁体和铰缝同时损伤情况，对铰接板法进行参数修正，重新推导荷载横向分布计算方法，为损伤桥梁承载能力评估提供依据。

1 损伤参数的定义

1.1 铰缝传力削减

对于空心板之间通过铰缝连接的多梁式板桥结构，设有单位正弦荷载作用在1#空心板轴线上，沿铰缝处纵向切开，每一切缝处引入大小相等、方向相反的剪力gi。图1为铰接板桥的基本体系。

图1 铰接板法的基本结构

计入铰缝损伤情况，剪力传递会发生削减，引入剪力折减系数μ，考虑到每处铰缝损伤程度不一，假设各铰缝折减系数依次为μ1，μ2，μ3，…。根据力法原理，其表达式为：

[δ]{X}+{Δ}=0

(1)

式中：δ为计算系数，即单位力在i处引起的变位,按式(2)计算；X为铰缝处剪力,按式(3)计算；Δ为外荷载p在i处引起的变位,按式(4)计算。

(2)

(3)

(4)

1.2 主梁损伤削减

结合梁体外观检测，结合文献[4]中裂缝参数特征对空心板的静刚度损伤折减情况进行量化评估。引入裂缝宽度系数θ和裂缝高度系数λ，公式如下：

(5)

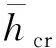
梁体的静刚度折减系数ξ采用下式计算：

(6)

根据各片板梁刚度实际退化情况，得到刚度折减系数ξ1,ξ2,…,ξn。损伤后梁体刚度评估值Ei按下式计算：

Ei=ξiE

(7)

式中：ξi为刚度折减系数，0<ξi≤1；E为原梁体的刚度。

刚度变化必然影响力法方程变位系数改变，由梁的挠曲线微分方程和扭转理论可推得简支梁跨中产生的竖向挠度和扭转角。x=l/2时，单位荷载作用在刚度发生损伤板梁中央所产生的挠度w为：

(8)

扭矩为b/2sin[(2x)/l]，x=l/2时，单位扭矩对刚度损伤板梁产生的截面扭转角φ为：

(9)

式中：b为板宽；l为桥梁纵向跨度；I为抗弯惯矩；G为抗扭惯矩，G=0.425E。

考虑到每片板的挠度、转角均受刚度E和折减系数ξi的影响，统一起见，引入变位系数矩阵[δ]的转化系数ki，ki=1/ξi。

2 修正的铰接板法方程建立及求解

根据力与变形之间的关系可确定上述正则方程中的常系数值并规定其正负，变位与赘余力素正向一致时取正值，反之取负值。如图2所示，单位铰接力下变位的表达式为：

(10)

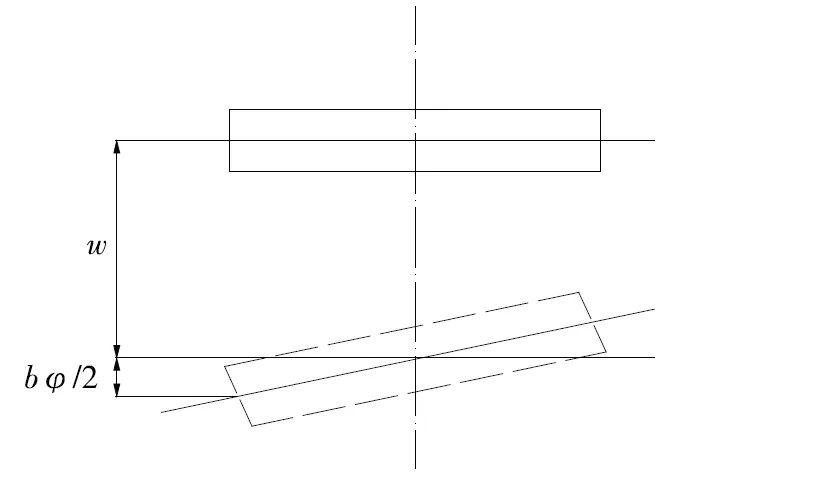
图2 变形示意图

外荷载p作用在i号梁时，有：

(11)

(12)

(13)

将各项系数代入第一节力法方程中，编程计算gi，然后根据铰缝传力折减系数μi求得实际剪力值如下：

单位荷载作用于1#梁时，横向分布系数竖标值如下：

(14)

同理可得其他各梁竖标值。

3 算例分析

某在役装配式空心板桥上部结构由9片预应力空心板组成，跨径13 m，采用C50砼。由于钢筋对截面的刚度贡献较小，为便于和理论分析统一和对比，仿真建模时不考虑预应力钢筋、普通钢筋及铺装层作用。空心板标准横断面见图3。

图3 空心板标准横断面(单位：cm)

为精确模拟铰缝损伤和梁体刚度损伤，采用ANSYS建立实体单元模型进行仿真分析，单元类型为Solid65，根据损伤定义不同构造处的材料特性进行分析计算。铰缝损伤的量化评估采用文献[5]中的公式：

(15)

式中：li为完整未损伤铰缝长度；l为铰缝通长，即桥梁跨径。

实桥损伤后刚度根据该桥裂缝开展情况及参数特征值，通过式(6)计算。刚度折减系数如下：

(16)

式中：Ei为每片板评估刚度；E为原始设计刚度。

读取每种工况下梁的挠度值，根据下式计算影响线竖标值ηij：

(17)

式中：fi为单工况下某块板的跨中挠度；∑fi为各板跨中挠度值之和。

为简化计算，并便于对比分析，假设梁体损伤在同等自然和车辆荷载条件下对称出现。但实际上各梁板损伤一般非对称，应视具体情况具体分析。以边梁1#梁和中梁5#梁为例，计算结果见表1。

从表1可看出：修正铰接板法所得竖标值与传统铰接板法计算结果有出入，荷载施加在某片板时，其变位即竖标值明显增加，远离荷载的板其竖标值有所减小；离荷载作用位置越远，竖标值减小幅度越小。其原因是修正铰接板法综合考虑了铰缝传力削弱和刚度退化的影响。由于实体单元建模同样考虑了铰缝和主梁刚度的损伤，有限元法竖标值计算结果更接近于修正铰接板法，最大误差不超过1%。修正铰接板法与实体仿真建模结果更接近，其计算精度更高。按照修正后的方法对既有损伤桥梁进行受力计算和承载力评估，可为桥梁工程加固的精确计算提供依据。

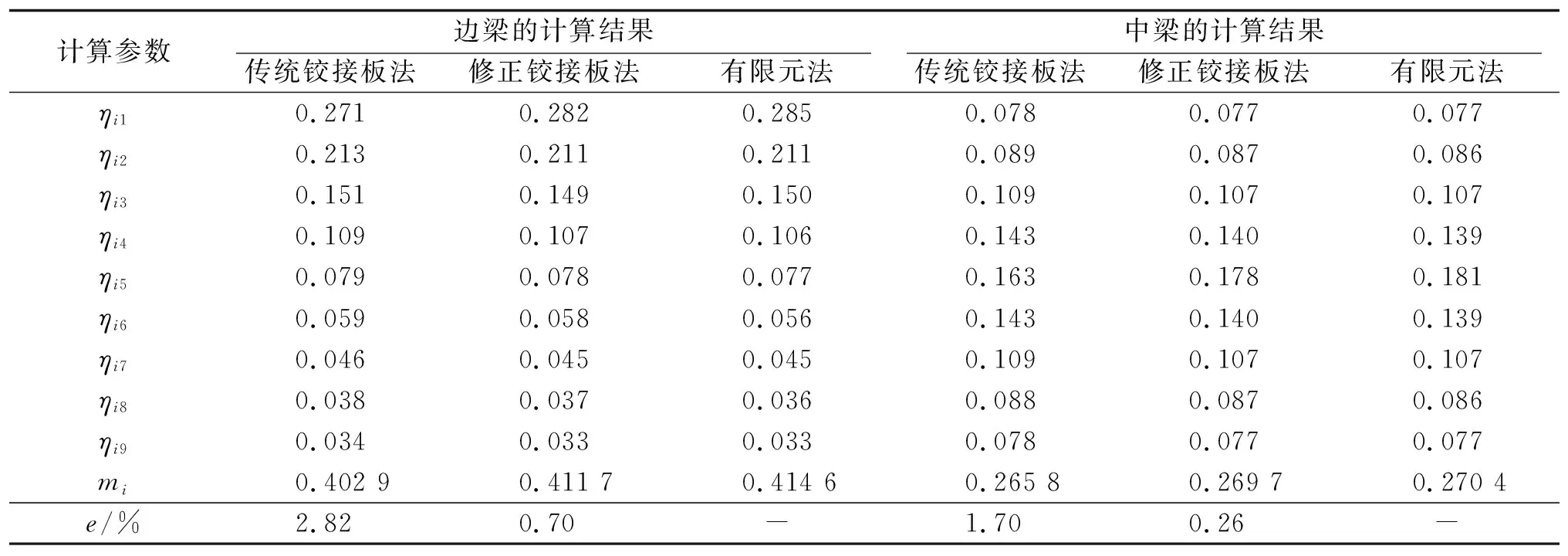
表1 边梁和中梁影响线竖标及横向分布系数

4 结论

(1) 考虑铰缝和梁体损伤的修正铰接板法的计算结果与有限元分析结果接近。

(2) 对于铰缝和主梁均发生损伤的在役空心板桥，传统铰接板法精度不足；修正铰接板法综合考虑了铰缝损伤和梁体刚度退化的影响，符合在役桥梁实际受力特点，其计算结果更精确。