声学超表面的研究与应用进展

郭晨冰， 赵 铮， 许卫锴

(1.中国船舶重工集团公司第七一三研究所， 郑州 450015； 2.南京理工大学能源与动力工程学院，南京 210094; 3.沈阳航空航天大学辽宁省飞行器复合材料结构分析与仿真重点实验室， 沈阳 110136)

近年来，人工结构材料的研究工作取得了异常突出的成绩。不同于自然界中存在的一般材料，人工结构材料代表着一种全新的理念，在遵循自然界原有的自然规律及物理学领域的基本规律情况下，它可以实现自然材料所不具备的新功能。迄今为止，科研人员已经实现了人工结构材料与多领域的交叉融合，实现了在电学、光学、声学等领域的应用，为新时代的信息传递开辟了新的纪元。其中，声学超材料[1-4]作为人工结构材料在声学领域内的一种应用，因其超强的声波操控能力，已经成为当前的一个研究热点。例如，利用声学超材料对声波的异常反射和折射特点，可以实现一些特殊的应用需求，如声学聚焦、隐身、吸收、伪装等。

然而，对于常见的超材料来说，仍存在体积大、制作成本高、工作带宽窄、能量损耗大等缺点，同时加工制作也会存在一定的难度。因此，在保留声学超材料的功能的同时，如何实现将其轻薄化是目前亟须解决的问题。声学超表面[5-7]的提出即是实现这一目标的产物，是最近几年声学超材料的重要研究分支。声学超表面是一种类似于声学超材料二维化的结构，实现了超材料的轻薄化，其在厚度方向上达到了亚波长尺度，且超薄的结构尺寸可以满足微型尺寸操控大波长声波的要求。由于具有灵活的可设计性，因此声学超表面具有广阔的应用前景，并成为当前声波调控领域的研究热点。现从超表面的相位调制机理、分类及展望等几个方面介绍当前声学超表面的研究进展。

1 超表面的相位调制机理

根据波动理论，当波在不同介质中传播时，到达界面应满足斯涅尔定律。对于均匀的介质，波首先在折射率为ni的介质中传播，经由介质界面向折射率为nt的介质入射，则反射角θr和折射角θt可由斯涅尔定律确定[8]。然而，对于非均匀介质，波的传播将会出现有趣的现象。根据费马原理，波在不同的介质中传播时，如图1所示，从A点到B点的光程(或声程)应为最小值。其中，光程或声程的定义为介质的折射率和波在物理空间中实际的几何路程的乘积，即

图1 广义斯涅尔定律推导示意图Fig.1 Schematics used to derive the generalized Snell’s law of refraction

Δ=nr

(1)

式(1)中：Δ为光程或声程；n为介质的折射率；r为实际的几何路程。若波连续经过几种不同的介质，其光程/声程为

(2)

如图1所示，假设波由A点入射到达B点，则其相位的变化Ψt(x)应为

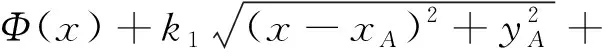
(3)

式(3)中：φ(x)为波的相位；ki为不同介质的波数，ki=2π/λi，其中λi为波长。由于光程/声程最小，因此对式(3)求导得

(4)

整理式(4)得

(5)

同理，可得反射的关系式，即

(6)

式中：θi、θt、θr为入射角、折射角、反射角。

式(5)、式(6)称为广义的斯涅尔定律[9]，相位梯度dΦ(x)/dx的存在使得反射波和折射波的方向发生改变，产生异常的反射或折射现象。如果不放置超表面，即没有此相位梯度时，这两个公式将退化为常规的斯涅尔定律。

2 声学超表面的研究与应用

由广义斯涅尔定律，只要找到能实现相位梯度的材料，通过合理地排布超表面的单胞以实现预期的相位调制，即可实现各种新颖的应用。下面将通过不同类型的声学超表面进行讨论。

2.1 空间卷绕/折叠结构型超表面

波在传播中的相位与其走过的路径长短有关，因此通过调整波的传播路径长度可以达到实现相位调制的目的，而空间折叠结构具有易于调整声波传播路径的特点，为超表面的相位调节提供了一个方向。Li等[10]首先提出一种由超薄空间折叠结构组成的超表面，如图2所示。调整几何尺寸可以改变声波的传播路径长度，从而实现0～2π的离散相移[10]。通过适当设计单元的几何形状，该课题组从理论和实验两方面验证了声波的自由操控[11]，并随后将其扩展到了各个应用领域[12-15]。Qiu等[16-17]则利用类似的折叠腔实现了声波的异常折射和聚焦现象。

图2 空间折叠结构超表面及其相移特性Fig.2 Acoustic metasurfaces based on the labyrinthine structure and its phase shifts characteristic

然而，空间折叠结构往往具有迷宫的构型，传播路径狭长，因此会导致能量损耗较为严重，为了减小能量的损耗，Li等[11]使用了四种不同类型的迷宫单元(每个单元具有特定数量的板和合理的宽度)来提供足够的相位延迟，如图3所示。符号(i,j)表示一个迷宫单元从顶部和底部分别挤出i块和j块板材。较小的i和j意味着更小的损耗。另一方面，迷宫结构与空气会产生阻抗失配的缺点。为了改进超表面的阻抗匹配问题，Xie等[18-19]将方形的迷宫构型改为螺旋形或圆锥形的结构，利用3D打印技术制作了空间卷曲的迷宫型声学超表面，并观察到了该结构的负折射现象，如图4所示。这种空间卷曲的超表面的阻抗失配问题得到了良好的改善，可以实现完美衍射的声学透镜[20]。

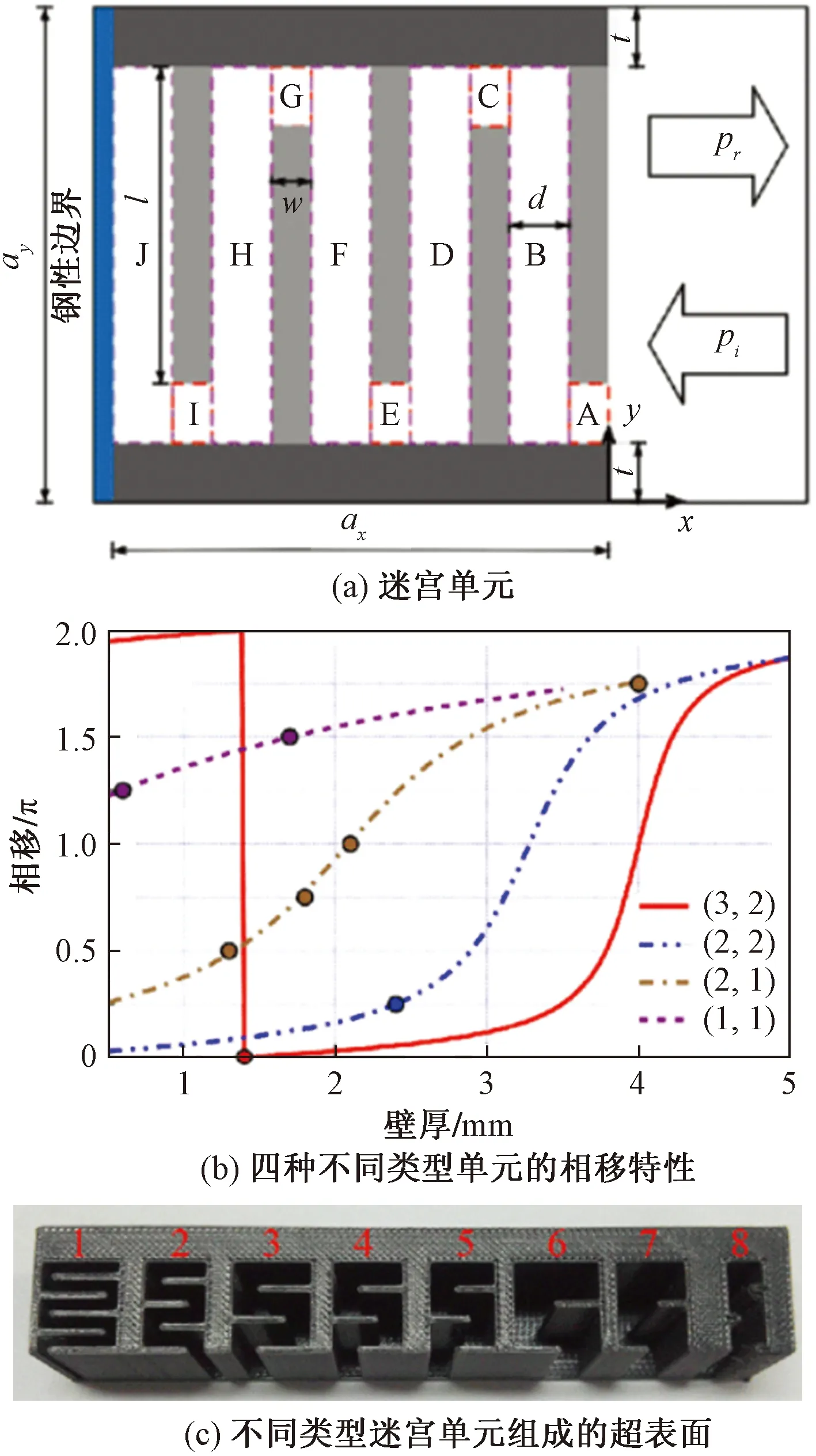
图3 迷宫单元型超表面Fig.3 The specific labyrinthine-type metasurface

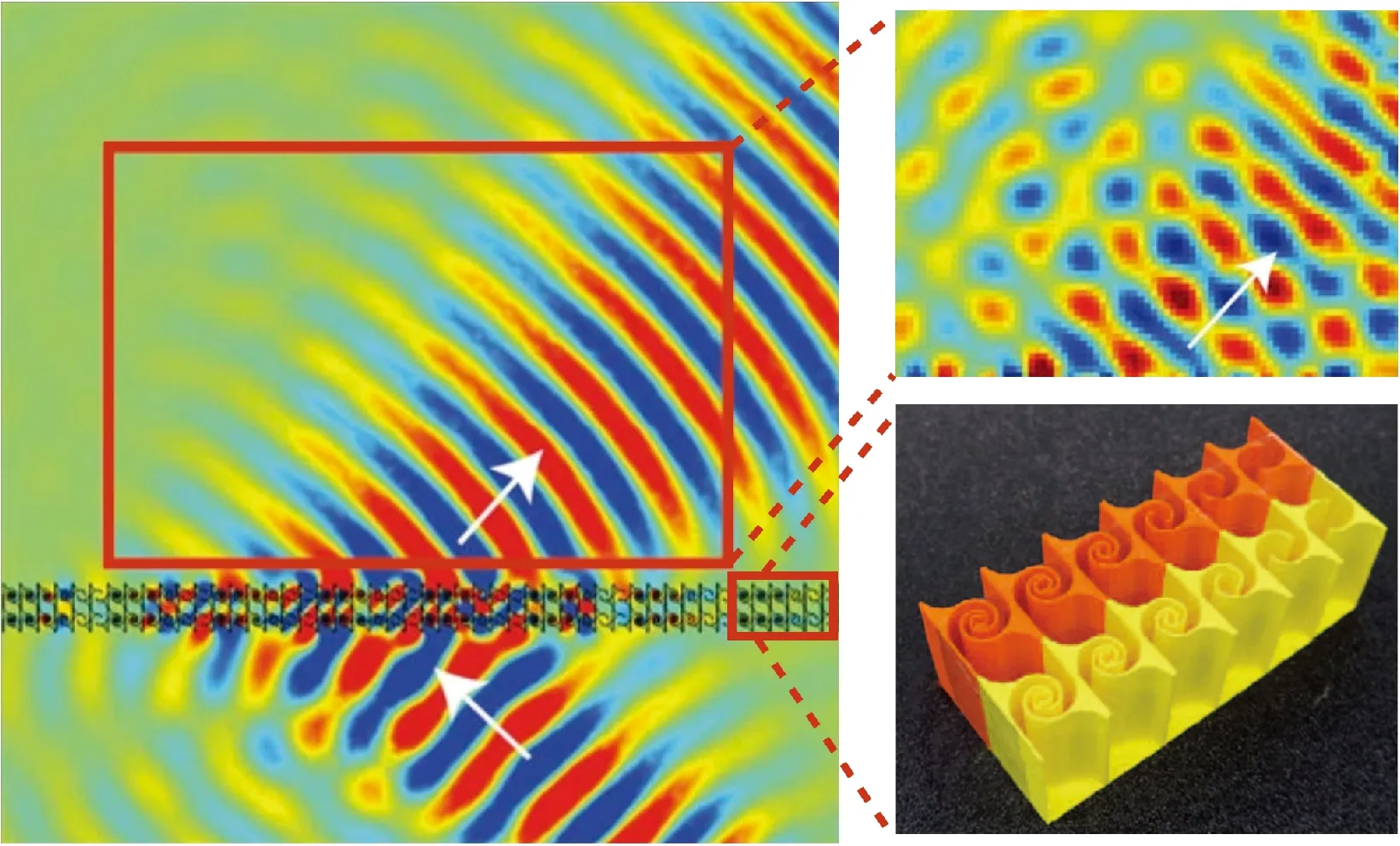
图4 迷宫型超表面及负折射现象Fig.4 Tapered labyrinthine acoustic metasurface and negative refraction

2.2 Helmholtz谐振型超表面

除了空间卷绕/折叠结构外，声学的Helmholtz谐振器也可以提供相位的调节。尽管单个Helmholtz谐振器所能提供的相移有限，但四个串联的Helmholtz谐振器可以实现大范围的相移[21]。然而，与单个Helmholtz谐振器相比，这种连接增加了与空气的阻抗失配，从而导致更低的传输效率，因此仅仅基于Helmholtz谐振器的超表面更适宜用于调控声波的反射[22]。Zhao等[23]发现，Helmholtz谐振器可以产生双重反射，一种是普通的反射，另一种是遵循广义斯涅尔定律的异常反射。为了克服阻抗失配的缺点，可以利用其他的结构与Helmholtz谐振器配合组成新的超表面。例如，Lan等[24]将四个周期排列的Helmholtz谐振器与一个金属板组合起来，两者之间存在一个狭缝，如图5所示。通过调整狭缝的大小可以方便地实现声速的离散分布和阻抗的匹配，并具有较宽的频带和高效的传输特性。Xie等[19]、江雪等[25]将Helmholtz谐振器连接在一个直管上，该直管高度可调而宽度固定为λ/2，利用Helmholtz共振和Fabry-Perot共振之间的耦合，可大大增强超表面的透射率。

图5 带有金属板的Helmholtz型超表面Fig.5 Helmholtz-resonator structure metasurface with metal plate

2.3 薄膜结构型超表面

除了异常反射和折射，声的吸收、衰减和减弱也是一个重要的课题。薄膜结构可以产生较大的位移，从而达到吸收能量的目的。研究人员发现，利用薄膜结构的谐振和反谐振特点，可以实现声波的全反射[26-27]、全透射[28-29]和负折射[30]等异常现象。Ma等[31]设计了一种基于混合谐振的薄膜型吸收器，该吸收器包含一个反射膜谐振器，将其放置于阻抗匹配的全反射超表面上，并用密封的具有绝热系数的气体层进行隔离，由此产生的混合谐振将得到两个有用的模态，其归一化的振型如图6所示。这种基于混合谐振的设计只需要具有微弱本征损耗的材料就可以实现完全吸收，因此与传统的吸收机制是一种截然不同的机理。同时，超表面的吸收特性显示出一个非常尖锐且近乎完美的吸收峰，证实了阻抗与空气的匹配，因此薄膜型超表面体现出了非常大的优势，从而得到了广泛的研究[32-34]。然而，薄膜型超表面也具有明显的缺点，如制作复杂，相对也比较脆弱。

图6 薄膜型超表面及其谐振特征Fig.6 The membrane-type metasurface and its resonance characteristics

2.4 其他超表面研究

目前，声学超表面正在得到越来越多的关注，许多其他类型的声学超表面也得到了研究和发展。例如，Zhao等[35-36]提出一种可自由配置的主动型超表面，将压电换能器(PTs)产生的声波能量集中到特定区域，从而实现声波聚焦的目的。Ding等[37]提出了一种由具有负模量的声学开口球型谐振腔阵列组成的声学超表面模型，模拟了四种异常反射，验证了广义斯涅尔定律。Boutin等[38]则提出了一种具有内部共振的弹性波超表面，并实验验证了对机械波的操控。Zhu等提出了一种由局域共振的环形锥体构成的超表面，通过选择锥体的尺寸，使入射波具有精准的相位便宜，从而影响其折射特性；之后又提出一种全内反射的超表面，实现弹性波在薄波导中传播时的高效隔振[39-40]。Li等[41]利用一组具有负电容的压电换能器设计了具有自适应调制波前的超表面。Liu等[42]提出一种“几”字形的超表面，并实现了源错觉和声涡旋的现象。Xu等[43-44]则针对无损检测的理念进行逆向操作，利用兰姆波与缺陷的交互作用所产生的信号变化以调制起波前相位，设计出了单槽型和双槽型的声学超表面，实现了波的异常折射、任意轨迹传播和源错觉装置。Tian等[45]设计了满足阻抗匹配的五模结构超表面，如图7所示。该方法能有效地处理宽频段的折射波。Li等[46]通过耦合不同的谐振器并产生混合谐振模式，设计并制作了一种具有亚波长尺度的超表面单元，并实现了完美的声波吸收。总之，声学超表面已成为当前研究的热点，有关的新构型层出不穷，研究范围也随之不断地延伸。

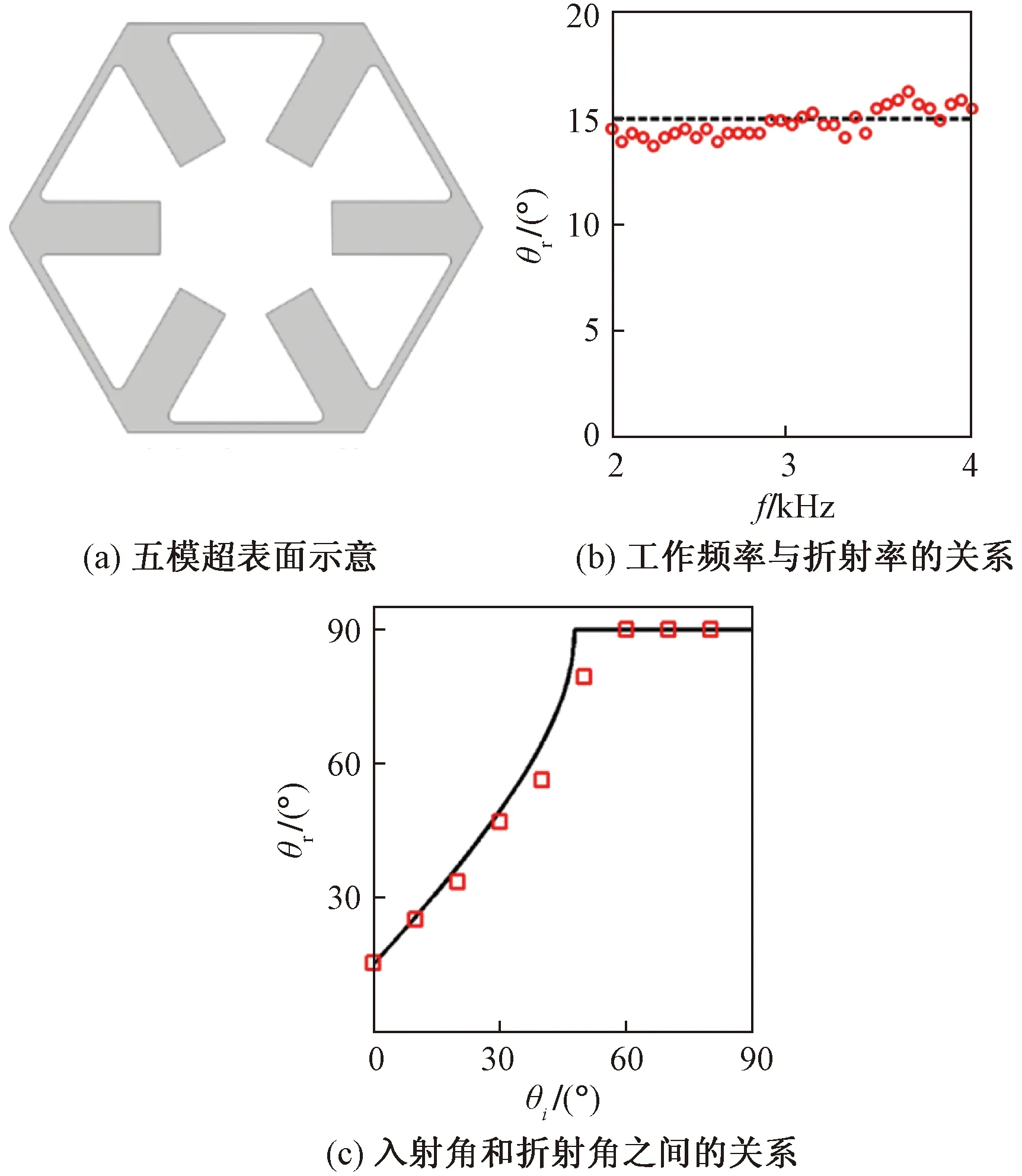
图7 五模超表面Fig.7 Schematics of the pentamode metasurface

3 讨论与结论

声学超表面的出现为声波的调控和声学器件的研究开创了革命性的契机，为当前的控波技术实现了创新的理念。目前，常见的声学超表面主要包括空间卷绕/折叠结构型、Helmholtz谐振型、薄膜结构型、压电材料型及五模超表面等。尽管已经取得了巨大的成就，但现有的声学超表面仍然存在一些缺点，在声波/弹性波的任意调控方面仍有很多工作亟须完成。

(1)无论是迷宫型还是谐振型的超表面，容易存在工作带宽较窄的问题[7]。因此，可调谐的声学超表面也得到了广泛的关注，如Xie等[47-48]利用局域共振的二元结构作为构建单元或编码以组成可编程超表面，可以实现宽频带或多频带的超表面设计。Zhao等[49]、Yuan等[50]设计出一种类似螺杆螺母的“鱼骨”型机构，在四周设置完美匹配层(perfectly matched layer, PML)以吸收进入域内的所有波，当高斯波入射时，拧动螺母即可调控相位。Li等[51]通过调整损耗型超表面的入射角度以达到调谐其传输特性的目的。Tian等[52]则在Helmholtz谐振腔内以泵入或泵出液体的方式来实现调频的控制。

(2)在面向应用的器件设计中，由于设计的复杂性，需要在超表面的厚度、通道长度、组成材料和制造过程等影响因素中进行权衡，具有试凑的性质，依赖于设计者的经验。解决这一问题的途径之一是声学超表面的拓扑优化设计。超表面的拓扑优化设计在光波和电磁波领域已经得到了一系列的研究[53-56]，并有向声波和弹性波领域发展的趋势。如Noguchi等[57]利用水平集拓扑优化方法，在声-弹耦合系统中将纵向的声波转化为横向的弹性波以达到降噪的目的。Miyata等[58]设计了同时考虑通风性和隔音效果的超表面。Ahn等[59]则利用有限元方法和传递矩阵法计算单胞的相位延迟，设计出可将纵向弹性波异常反射的超表面。然而，相对而言，拓扑优化在声学领域，特别是对声学超材料/声学器件的研究应用较为滞后。建立系统的声学超表面拓扑优化体系将是声学超表面及器件研制的重要课题。

(3)目前存在的声学超表面大多数研究的都是在空气中传播的情况，而声学超表面在水下声学中的应用也将是一个重要的研究方向。Bi等[60]设计了一种适用于水下的隐身斗篷。Su等[61]利用五模超表面设计了一种基于折射率空间变化的水声宽频带聚焦透镜，并实验验证了聚焦效应。喻敏等[62]将声学超表面应用于水下声散射场的控制，讨论了超表面单元尺寸对水下声散射特性的影响。与空气相比，水与固体材料在声学特性上较为接近，这有利于设计出与水下环境阻抗匹配的结构，但此时空气中刚性壁的假设不在适用，需要考虑流固耦合效应以及黏滞层所带来的损耗。

综上所述，声学超表面的研究已经得到了广阔的发展，这为声波的调控提供了更多的可能性。根据目前的发展趋势，声学超表面会向着宽频带/多频带、低损耗、多功能、可调谐、易加工的方向发展，并根据人们的需求实现对声波的任意调控，解决目前工程技术中的一系列问题，如异常反射/折射、吸声、高清成像、水下舰艇的声呐隐身等控波需求。