音乐信号处理的特征分析综述

王力，王鑫，谢凌云

（中国传媒大学，北京 100024）

1 绪论

随着互联网的发展与普及，网络音乐应用逐渐成为人们聆听音乐的主要渠道。面对繁多的网络音乐，为适应用户对于音乐搜索的需要，对音乐内容识别分析并进行自动分类是当今迫切的需求，而这些都需依赖音乐信息检索（Music Information Retrieval，MIR）。音乐信息检索往往可以分为基于音频内容的分析和基于文本（如歌词、用户评分、出版年份等等）的分析，前者的音乐特征由音频特征构成，后者则由语义特征构成。

音频特征提取是音频内容分析的一个重要阶段，也是模式识别和机器学习中必不可少的处理步骤。它通常使用几十个或数百个特征来描述一首完整的歌曲，大幅减少了要处理的数据总量，并去除了与音乐分析任务不相关的冗余信息，同时也将原始数据转换为更合适的表示形式［1］。

传统音频特征大多具有一定的物理意义，它们分别描述了信号中不同维度的信息，如时域、频域相关特征。近年来，人们对于特征提取的研究主要体现在提出更加准确描述乐理概念或符合心理声学规律的音乐类特征；此外，随着深度学习技术的发展，越来越多的音乐信息检索任务倾向于数据驱动［63］，由机器自动学习音频中的内容信息，特征不一定具有具体意义，甚至不一定能被人理解，例如神经网络直接将信号波形或时频图作为输入特征。近年来，这些深度特征被广泛用于声学场景分类［64］和音频视频分析［65］领域。

本文对面向传统机器学习的音乐信号特征与面向深度学习的音乐特征进行了全面的综述与梳理，总结了各类主流音频特征的含义、计算方法及应用现状，最后介绍了用于特征提取的常用工具。

2 音乐信号的预处理

在计算音频特征时，通常需根据任务需求对原始音频进行预处理，使原始音频转化为更加合适的形式来方便特征的提取。常见的预处理方式有下变换、直流消除、归一化、信号分帧和加窗。

2.1 下变换

对于多声道信号，可转化为单声道以降低数据量［2］。在下变换时，通常采用计算多个声道采样值的算术平均值来实现，也可对某些声道加以不同的权重，如5.1声道中的环绕声道便可设置较小的权重。

2.2 直流消除

直流偏移量通常不会提供任何有效信息，并可能对特征计算结果产生不必要的影响，通常从每个样本点中减去全部信号的算术平均值可达到消除直流的作用。

2.3 归一化

为了避免不同输入信号的幅度差异对特征提取的影响（尤其在强度类特征中），可将信号归一化为具有预定（最大）振幅或功率的信号。归一化音频信号的一种简单而常用的方法是检测其绝对采样值的最大值，并缩放信号，使该最大值的绝对值映射到1。

2.4 信号分帧

部分特征提取算法要求对信号进行分帧处理，在特征提取时分别对每帧进行处理，需根据实际音频特点以及处理的目标来设定帧长，帧移和窗函数，即可得到分帧信号。对每帧信号提取特征值，可得到反映沿时间轴或频率轴动态变化的信息。

2.5 加窗

由于DFT算法需对信号进行周期延拓，为避免信号在延拓过程中产生奇点而导致谱泄漏，需事先对信号进行加窗处理，根据信号的不同来确定合适的窗函数。在音频信号处理中，常用的窗函数有矩形窗、三角窗、汉宁（Hanning）窗、汉明（Hamming）窗、布莱克曼（Blackman）窗等。

3 传统声学特征

音乐信号的传统声学特征主要指从音频文件中提取出来的基本物理特征，又称为初级特征，如强度、频谱等等，但通常没有直接的音乐含义，可分为时域特征与频域特征；除此之外，还能进行更细的类别划分。例如Peeters等人将声学特征具体分为时域特征、频域特征、能量特征、协和性特征和感知特征［4］；Alias等人将声学特征分为物理和感知两类，然后再分别按时间、频率、小波、图像、倒频谱等类别进行了细分［5］。本节将对常见的传统音频特征进行梳理与总结。

3.1 时域特征

时域特征的显著特点是它们不需要对原始音频信号进行任何形式的变换，而是在信号本身的采样值上进行处理，这种音频特征提取方法也是最基本和最经典的方法之一［5］，其涵盖基于过零率的特征、基于幅度的特征、基于能量的特征等。

（1）过零率

过零率（Zero-Crossing Rate，ZCR）定义为一秒钟内声音信号在时域上的穿越0 电平的次数，计算方法如式（1）所示。物理意义上ZCR与信号频率一定程度上存在相关［18］。

其中，N 为采样点数，x(i）为信号在第i 个采样点的幅度，下同。

（2）能量

信号的能量（Energy）为采样点的平方和，如式（2）所示。在音频分析中，以帧为单位可组成分帧能量序列。

此外，还有均方根能量（Root-Mean-Square，RMS），定义为信号各采样数据能量和的平方根，如式（3）所示。

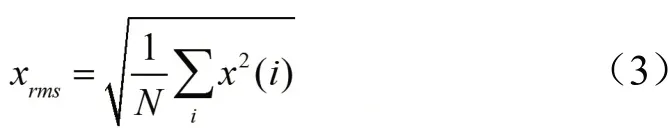
（3）低能量帧比值

低能量帧比值（Low Energy Rate）计算了低于平均能量的数据帧所占的比例，其意义在于检测瞬变信号以及脉冲。

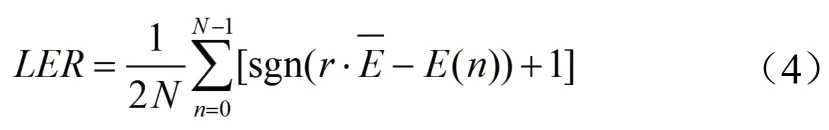
其中，N 表示音频帧数，E(n）表示短时能量值，表示该片段平均能量，r为阈值系数，可对平均能量进行加权来控制能量阈值的高低。

（4）ADSR振幅包络

ADSR［25］指代单乐音包络模型，包含起振（Attack），衰减（Decay），延持（Sustain），释放（Release）四个阶段，如图1所示。在特征计算中，通过ADSR包络模型可以提取几个特征，分别是：起振时间（Attack Time），即波形起始最低点到最高点所用时间；对数起振时间（Log Attack Time，LAT）；起振跨度，即起始最低点到最高点的幅值跨度；起振斜率，即起始最低点到最高点的幅值变化斜率等等。其余三个阶段的特征计算方式同理。ADSR 模型广泛地应用于音乐合成领域，而LAT还可被用于环境声音识别［26,27］。

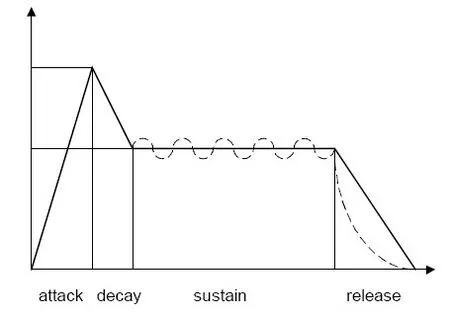
图1 ADSR振幅包络模型

（5）时域质心

时域质心（Temporal Centroid）是对信号时域波形采样值的一种统计度量，也可称为信号时域的一阶矩。时域质心表示信号能量分布上的时间重心，计算公式如式（5）所示，可应用于环境声音识别领域［28］。

3.2 频域特征

频域特征通常与音色密切相关，其中既有基于傅里叶变换（FFT）又有基于短时傅里叶变换（STFT）得到的特征，又可分为谱包络相关特征、谱结构相关特征、统计类特征和系数特征。

3.2.1 谱包络相关特征

谱包络相关特征从频谱全局的轮廓形状来描述信号，包含谱斜度（Spectral Slope）、谱熵（Spectral Entropy）、谱平整度（Spectral Flatness）、谱不规则度（Spectral Irregularity）特征。

（1）谱斜度

谱斜度通过线性回归的方法来拟合频谱包络，谱斜度就是其斜率［21］，如图2 所示。它表示了频谱能量在整个频段的分布趋势，可应用于语音分类和说话人识别问题［28,29］。

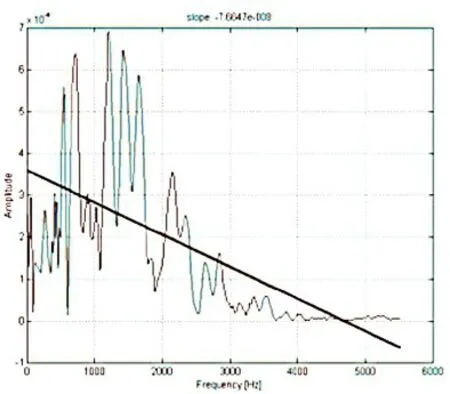
图2 谱斜度示意图

（2）谱熵

谱熵是频谱均匀性的度量，频率分布随机性越大，混乱度越高，谱熵越高。也可将信号划分L个频率子进行计算以达到更佳的音乐和语音识别效果，计算方法如式（6）所示。其中，Ef代表f0至fL-1子带的谱能量。谱熵可用于音乐于语音信号的端点检测和分割。

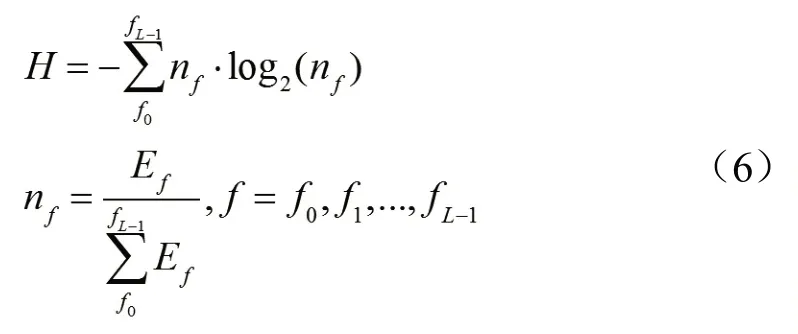
（3）谱平整度

谱平整度描述了频谱分布的平滑程度，为几何平均值与算术平均值之比［30］，如式（7）所示，它可用于区分噪声（谱平整度高）与音调（谱平整度低），以及音乐起始点检测、音乐分类等［31］。

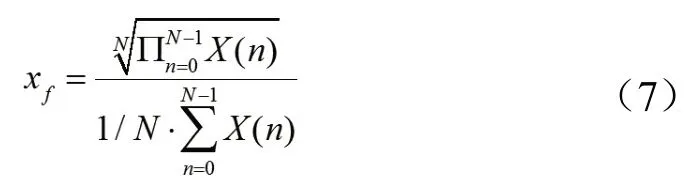
其中，N为单边谱采样点数，X(n)为信号频谱幅值，下同。

（4）谱不规则度

谱不规则度计算了谱包络上相邻峰值间的差异程度。一般有两种算法：第一种为相邻采样值之差平方和的归一化，如式（8）所示；第二种是当前峰值与连续3个谱峰之差的求和，如式（9）所示。

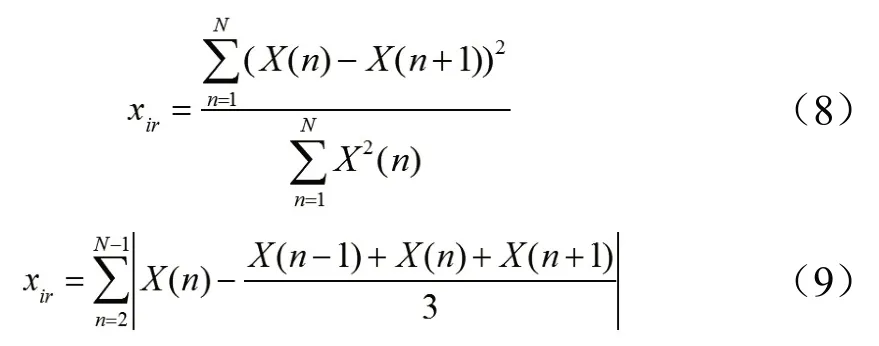
3.2.2 谱结构相关特征

谱结构相关特征从频谱局部的成分来描述信号，包括谱通量（Spectral Flux）、谱下降值（Spectral Roll-off）、频带能量（Spectral Energy Band）、不协和度（Inharmonicity）、谱对比度（Spectral Contrast）特征。

（1）谱通量

谱通量描述了STFT 帧间幅度差异，如式（10）所示，它反映了声音频率能量分布的变化情况，可用来检测音符起始点，测量信号功率谱变化的速度，在音乐识别、乐器分类等领域有着一定的应用［22］。

式中，X表示信号频谱幅值，N表示采样点数，k为STFT的帧数索引值。

（2）谱下降值

谱下降值定义的是频谱能量开始下降至某百分比的频率点，频谱能量下降系数通常可取85%-95%之间，可用来区分清音和浊音，音乐分类、音乐识别等领域。

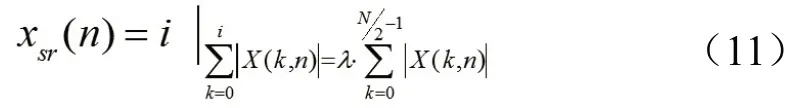
其中，i为谱下降值频点，λ为下降百分比，N表示采样点数。图3 为一段音乐信号的谱下降值点示意图，λ取85%，对应的谱下降值为6267 Hz。

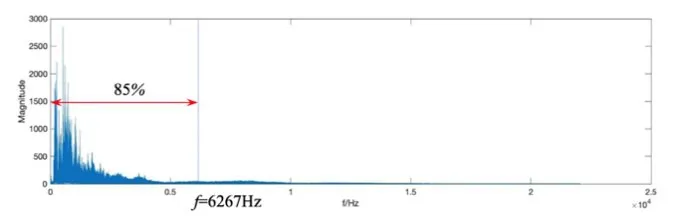
图3 谱下降值示意图

（3）频带能量

频带能量特征计算了音频频带的能量分布状况，可按照线性频率、对数频率、Mel频率、Bark频率、ERB尺度来划分频带，分别计算每一频带的能量，得到谱能量序列，描述信号的频谱能量分布。

（4）谱对比度

谱对比度是一个基于倍频程的音乐特征，它根据倍频程划分M 个子带，分别计算每一子带内峰值与谷值对比度数值，得到一个M 维特征。每个频带谱对比度的计算方法如式（12）所示。对于大多数音乐，频谱波峰大致对应于谐波分量，而波谷代表着大部分非谐波分量或噪声。因此，谱对比度特征可反映频谱中谐波分量与非谐波分量的相对分布。

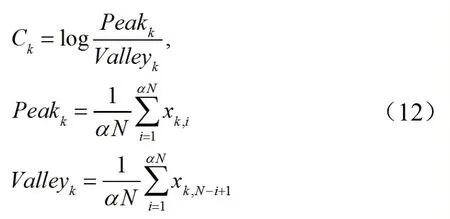
其中，k为频带索引，取值为1到M的整数，N为频带内的采样点数，α 为邻域因子，通常取0.02 到0.2之间［53］。

3.2.3 统计类特征

和时域特征类似，频域特征也有若干统计类特征，如一阶矩（谱质心，Spectral Centroid）、二阶矩（谱扩展、谱分布方差，Spectral Spread）、三阶矩（谱偏态，Spectral Skewness）和四阶矩（谱峰度，Spectral Kurtosis）。

谱质心是对信号频谱质心的描述，可认为是频谱的“重心”，如式（13）所示。谱质心与信号明亮度有关，信号明亮度越高，谱质心的值越高。可用于音乐分类、起始点检测。

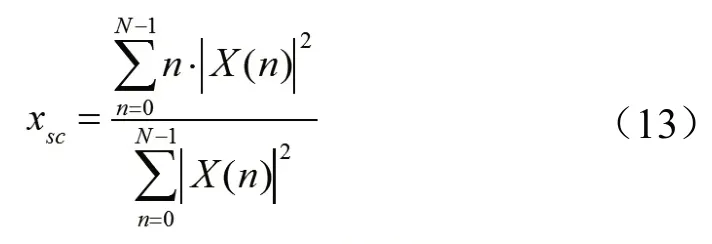
谱扩展（谱分布方差）描述了谱分布相对质心的离散程度。低值的谱扩展对应的信号频谱集中在频谱质心附近。谱偏态衡量了谱分布的对称性，对称分布的频谱偏态为0；而谱峰度是对频谱“非高斯性”的度量［2］，越偏向正态分布，峰度越小。

3.2.4 其他特征

音频分析中其他常用的频域特征包括Mel倒谱系数（Mel-Frequency Cepstrum Coefficients,MFCC）、线性预测系数（Linear Prediction Coefficient,LPC）和感知线性预测系数（Perceptual Linear Prediction,PLP）等等。

（1）Mel倒谱系数

MFCC是信号的一种倒谱表示，其中频带按照Mel尺度划分，而非线性尺度，可以看作是一种对音频信号频谱特性的描述方法，在音频信号处理领域应用广泛。MFCC的计算首先对信号进行DFT，再通过Mel尺度滤波器组，其通常为一组滤波器个数为L的交叠的三角滤波器组。Mel尺度根据心理声学的实验观察结论，引入了频率扭曲效应［46］，实验表明，人类听觉系统能够更容易地在低频区域区分相邻的频率，Mel频率可按照如下公式计算：

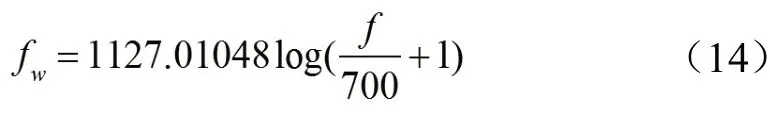
最后计算每个Mel滤波器输出的归一化能量Ek，其中k=1,2,···,L。最后用离散余弦变换（DCT）对其进行去相关处理，求得一组正交化的MFCC系数，计算公式如下所示。通常取前12-13个系数作为最终结果。

MFCC在语音信号处理领域应用广泛［61］，在音乐信号处理中可被用于音乐分类、歌手识别［32］，但目前没有明确的物理意义，无法用来解释结果。

（2）线性预测系数

线性预测系数的原理是根据过去的已有采样值的线性组合来预测当前的采样值，如式（16）所示，通过最小化预测误差来确定最佳滤波器系数,其可用一种全极点滤波器来表示，如式（17）所示。在发声模型中，一种比较主流的模型是激励源-滤波器模型。该模型的传输函数与LP的传输函数相同。LP用在该模型上，可以分离声门激励源和声道共振腔，在分析信号的包络谱和共振峰上有着重要的应用，还可应用于乐器发声模型和语音信号处理，并广泛应用于语音编码的识别，也被用于音乐分类［33］。

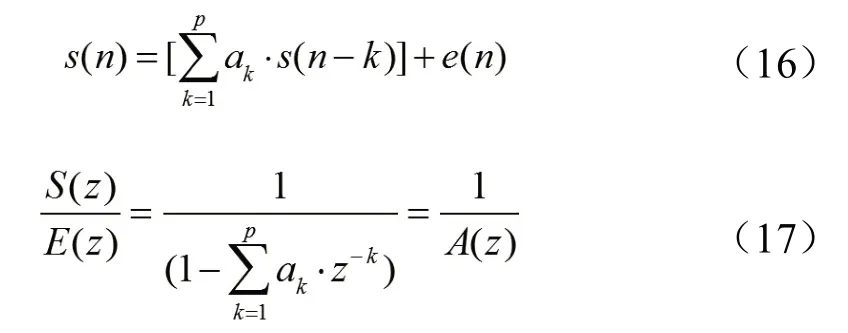
4 音乐相关特征

音乐相关特征可通过对初级特征进行进一步的处理而得到［2,3］，往往在一定程度上可以表征各类音乐属性，如节奏、速度、调式、和弦等等。

4.1 音高相关特征

（1）音高

乐音的音高由基频决定，MPEG-7标准将基频特征定义为局部时频分析的自相关函数第一个峰值［36］。此外，基频的提取还可通过过零率、平均幅度差函数、AMDF加权自相关函数等多种基于自相关的算法、基于谱分析的算法、基于倒谱的算法以及它们的组合［37］。在实际提取基频的过程中，会在一定范围内产生波动，研究表明，人的听感会趋于波动中心值［38］。

（2）Chromagram与音级分布图

Chromagram为基于信号时频谱图的特征，将时频图的频率坐标映射为音乐中对应的音级，即可得到Chromagram。音级分布图（Pitch Class Histogram）的计算方法是将每帧的DFT信号根据十二平均律音级划分为12组，计算某个音级对应的DFT所有频率能量之和，也可采用峰值能量、对数幅度均值等其他方法表示，如式（18）所示：

其中，Sk为对应DFT 系数组的频率子集，Nk为Sk元素个数。在分帧特征提取时，音级分布向量vk为一帧当中的计算结果，由此可生成矩阵V，其中元素可表示为Vk,i，k和i分别表示音级和帧数。可以看出，V是音级分布向量序列vk的矩阵表示，也被称为音高色谱图［1］。此外，除可计算12 音级分布图以外，还可使用音分，或128个MIDI notes 等其他标准来计算音级分布图。

Chromagram 与音级分布图表示了一段音乐信号中音高的分布特征。基于人耳音高感知机理，Chromagram 和音级分布图将不同八度内的倍数频率音高都整合到一个八度内表示，把频率能量映射到12个音级上，即可得到12维的特征向量，由此可计算出和弦、调性等特征［62］。

图4 为F大调合唱《As Long as I Have Music》音乐钢琴伴奏片段的Chromagram分布图，如图所示，横轴为乐曲节选时间（10s-20s），纵轴为十二平均律音级，该图表示了音级能量分布随着时间变化的情况。图5为上述片段的音级分布图。在音级分布图中，横坐标为十二音级，纵坐标为音级能量，可看出F大调主和弦F、A、C三个音级能量相对较高，而F大调调外音级能量很小。

图4 Chromagram分布图

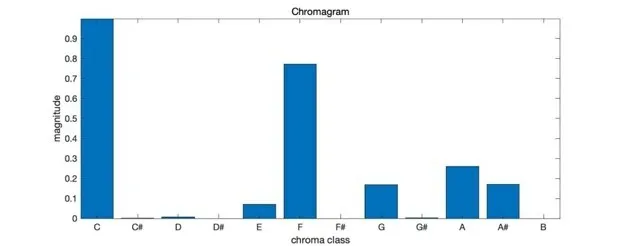
图5 音级分布图（Pitch Class Histogram）

（3）音调质心与和声变化检测函数

Christopher Harte等人从音程关系入手来研究，提出了音调质心（Tonal Centroid）这一概念［80］。将上文所述的音高分布向量映射到如图6所示的纯五度、小三度和大三度三个平面维度，并将三个平面的坐标汇集为一个六维向量，将其称为音调质心。

图6 音调质心的三个平面维度

如图，0-11代表从C音开始的12音级，图中展示了A大三和弦的音调质心，其包含的音级为A（9），C#（1），E（4），音调质心为图中A点所示位置。

不同音频帧的音调质心的变化，可以表征音乐的动态特性。于是通过计算音频帧间音调质心向量的欧式距离，可以得到和声变化检测函数HCDF（Harmonic Change Detection Function），该特征用来表示音乐中谐波内容的变化，可以表征连续帧之间和声变化的情况，在音频分割、和弦识别、音乐情感识别和音乐分类中都起着一定作用［54］。

（4）调谐频率

调谐频率的计算是调性检测、和声检测的基础。目前有多种方法可以计算调谐频率，如Scheirer使用了一组窄带通滤波器，它们的中频位于特定的频带，这些频带根据先前分析的乐谱精心挑选，以匹配音调。滤波器扫过一个小的频率范围，然后估计的调谐频率由所有滤波器组输出能量总和的最大中频确定［47］。Dixon提出在频域使用峰值检测算法并计算检测到的峰值的瞬时频率，然后对参考频率进行迭代修改，直到检测到的频率和参考频率之间的距离最小化［48］。

4.2 调式调性相关特征

调式由若干乐音按照一定的音程关系组织在一起，调性由调的主音决定。通常来讲，调式调性相关特征是基于上述音高相关特征得到的，Chromagram是调式调性相关特征计算的基础。

（1）调式调性与调值力度（Keystrength）

调性特征的计算即主音调值的计算。首先进行音级分布图的提取，估计音高分布，并基于音级分布图对所有可能的主音候选做互相关计算，得到调值力度（Keystregth）曲线，如图7所示，可以看出其峰值对应的调值就是调的主音F。求其峰值，获得沿时间轴排列的主音调值以及其清晰度。此外，在调值曲线上计算大调峰值和小调峰值的差，为正则偏向大调，为负则偏向小调。文献［39］以C大调和C小调为例得到了这两种调式每个音级的感知重要性的分布（Profile）。此外，还可根据模板匹配的方法得出乐曲的调式与调性，通过将曲目的音级分布图与各种调的特定模型如正交模型、全音阶模型、五度圈模型等进行比较，计算二者距离，如欧式距离、曼哈顿距离、余弦距离等，找到使二者距离最小的模型对应的调，就是曲目的调。

图7 调值力度曲线

（2）中国民族调式特征

以上调式特征都是基于西方大小调体系，对于中国民族调式，周莉等人提出基于模板匹配的中国民族音乐调式判别［40］。中国民间音乐的调式丰富多样，应用最广泛的是五声调式和以五正声音阶为基础的各种调式。以五声调式为基础，在角-徵、羽-宫两个小三度之间加上1个音，使五声调式得以扩大成六声调式或七声调式，这些增加的音称为偏音。通过提取旋律中所有的音高来判断有无偏音，并确定该旋律所属的模板来进行匹配：无偏音的旋律归属于中国民族音乐五声调式模板，有偏音的旋律归属于中国民族音乐七声调式模板。然后再通过若干调式特征进行核验，最终确定中国民族音乐的调式。

4.3 节奏相关特征

节奏相关特征是对音乐律动的描述，包括了速度相关特征和节拍相关特征。

（1）Onsets

Onsets是描述音乐信号中音符起始的特征，是计算音乐速度的基础之一，与音符起振时间不同，它表示音乐信号中音符起始的时间点。Onsets有多种计算方法，3.2节所介绍的时域能量、谱通量、谱质心、谱熵、谱基频改变等特征均可用于Onsets检测。

（2）速度

乐曲速度常用BPM（Beats per Minute）表示。BPM即每分钟的节拍数，是描述音乐速度的特征。对于恒定速度的音乐片段，可首先求得Onsets检测曲线，用自相关的方法计算曲线的周期性，得到拍子的周期Δts，进而得到每分钟的节拍数BPM：

对于变速乐曲，由上述方法求得的平均速度不能代表听者的感知，因此可以通过计算相邻两拍之间的时间tb来测得第j拍和第j+1拍间的动态的BPM：

若想求出变速乐曲的整体速度，那么式（19）中给出的平均速度不一定与听者所感受到的整体节奏相匹配。Gabrielsson在文献［49］中提出了一种计算“主速度”的方法来取代平均速度，如式（20）所示。其忽略了乐曲引子部分和尾声部分可能出现的过于缓慢或自由的速度。此外，Repp 发现感知速度与Onsets 间隔（Inter-Onsets Intervals，IOIs）分布的平均值有着较好的相关性［50］。Goebl等人提出了一种模式速度，通过扫描拍间间隔（Inter-Beat Intervals，IBIs）直方图并选择最大位置作为模式速度［51］。

（3）节拍直方图

节拍直方图（Beat Histogram）是另一种重要的节奏特征，是一种可视化信号律动的方法，直方图的横坐标为BPM，纵坐标为节拍强度。有多种方法可以计算节拍直方图。Scheirer使用了一个由梳状谐振滤波器组成的紧密间隔滤波器组，并使用滤波器的输出能量作为拍频强度［55］。Tzanetakis和Cook将音频信号分成四个倍频带，并通过取绝对值进行全波整流（FWR）、低通滤波器平滑处理、降采样、DC消除四个处理步骤，提取每个频带的包络，再通过自相关函数确定包络规律，最后通过在索引范围内取三个峰值将其计入节拍直方图中［56］。此外还可使用小波变换将信号分解为倍频程，对每个子带中最显著的周期进行累加，生成节拍直方图。图8展示了一段音乐的节拍直方图，可以看出图中有两个峰值，分别对应这首乐曲的四分音符和二分音符的节拍。通过节拍直方图可计算得到若干特征，如直方图总和、最高峰相对振幅、次高峰相对振幅、最高峰值与次高峰值之比等等。节拍直方图可用于音乐分类［43］。

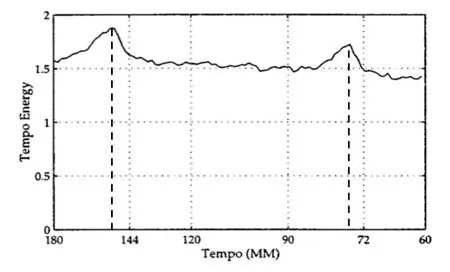
图8 节拍直方图示意图

4.4 感知相关特征

该类特征结合了人耳的感知特性，使特征参数符合人耳的听觉特性，描述了相应的人耳听觉感受，如响度、明亮度、粗糙度、尖锐度、以及不协和度等音质评价相关特征。

（1）响度

响度（Loudness）特征是表示人主观感知声音大小的特征。响度有多种计算模型，计算流程主要如下图9所示：

图9 响度的计算方法

响度的计算模型主要有Stevens响度模型、Zwicker响度模型和Moore响度模型。其中Stevens充分利用了等响曲线，将声音视为由一组倍频程滤波频带的几何平均值为中心的窄带噪声构成，用查图表法在等响度曲线图或者等声压级曲线图中找到该频率的位置，进而确定每个频带的响度指数，最后计算总响度级［57,58］。Zwicker通过使用1/3倍频带滤波器来近似临界频带进行滤波，引入外耳、中耳传递函数和混响场衰减，计算20个特征响度，将特征响度加入斜坡响度来模拟掩蔽效应，由此计算总响度［59］。Moore响度模型对频带划分进行了改进，利用了ERB坐标尺度取了372个中心频率，对应372个权函数（即滤波器）。对输入信号的频域能量，利用这些滤波器进行加权求和，得到372个能量激励，由激励级得到特征响度，进而求出总响度［60］。Moore响度模型2005年成为美国国家标准ANSI S3.4-2005。

（2）音质相关特征

其他感知相关特征还包括与音质评价相关的特征，如明亮度、浑厚度、粗糙度、尖锐度、不协和度等。

明亮度特征描述了某个截止频率以上的频谱能量比例，截止频率可根据实际需要进行调整，典型的明亮度截止频率通常可取1500 Hz左右。浑厚度可看作明亮度的互补特征，描述了某个截止频率以下的频谱能量比例，典型的浑厚度截止频率通常可取300 Hz左右。

粗糙度特征源自于文献［44］提出的纯音对感知不协和度曲线，描述了声音感知的不协和程度，该特征找出频谱的所有峰值对，每对峰值相乘，再通过不协和度曲线加权求和。

尖锐度特征计算与谱质心类似，但基于响度特征计算中的特性响度而不是幅度谱，特征反映了声音听感的尖锐程度，可看作谱质心的感知变体［4］［45］，可用于乐音分类及演奏风格和情感的判断。

不协和度表示信号频率和标准谐波分量的偏离程度，计算方法如式（21）所示。不协和度的取值在0到1之间，标准谐波信号为0，完全偏离的非谐波信号为1。现实生活中不存在完美和谐的乐器，普遍地，所有泛音分量都会比理论值偏高，且更高的泛音，偏离更明显。不协和度可用于乐器分类，中国民族乐器的不协和度普遍高于西洋乐器。

（3）感知线性预测系数

感知线性预测系数是在线性预测系数基础上发展出来的新特征［34］。它们的不同之处是PLP技术将人耳听觉感知的一些规律，通过近似计算的方法进行了工程化处理，应用到频谱分析中，将输入的语音信号经听觉模型处理后所得到的信号替代传统的LPC分析所用的时域信号。经过这样处理后的语音频谱考虑到了人耳的听觉特点。与传统LPC相比，PLP分析更符合人的听觉。Hönig等人又对算法进行了改进，可用于共振峰和谱包络估计［35］。

PLP技术主要在三个层次上模仿了人耳的听觉感知机理:(1）临界频带分析处理；(2）等响度曲线预加重；(3）信号强度-听觉响度变换。它的特征提取步骤如下图10所示：

图10 PLP系数的提取过程

5 面向深度学习的特征

前文所述特征在传统机器学习方法上被广泛使用，但由于音频特征与音乐类别之间的关系通常难以解释，机器学习的效果很大程度依赖于提取的音乐特征集。深度学习技术已被证明是一种从低级信息中提取高级特征的强大技术。随着深度学习技术的发展，基于深度学习的音乐信号分析方法开始涌现。得益于深度学习在图像处理的优异表现，在音乐信号中通常提取声谱图特征作为网络输入，避免了人工特征选择的问题。常用的谱图特征有短时傅里叶频谱图、梅尔频谱图和常数Q变换（Constant Q Transform，CQT）谱图。

5.1 短时傅里叶频谱图

一段音乐信号通常有数以百万计的采样点，会大幅增加计算资源，而傅里叶频谱图是一个相对紧凑的数据表示方法。与前文描述的特征不同，短时傅里叶频谱通过对时域和频域联合分析，可以更加全面、立体地帮助我们获取信号特征，它通过对信号分帧、加窗，把时域信号分解成无数小段进行傅里叶变换，最后在时间轴上堆叠变换后的结果，得到短时傅里叶频谱图。图11展示了一段中国民乐合奏乐曲片段的短时傅里叶频谱图。

图11 短时傅里叶频谱图

5.2 梅尔频谱图

由于人耳对频率感受的非线性特点，Stevens 在1937年提出梅尔尺度的概念，让人耳频率分辨与梅尔频率转化为线性相关，计算方法如3.2 节式（4）所示。梅尔频率能够更加充分地表示信号低频特征，压缩冗余的高频信号和噪声信号，广受研究者的青睐。梅尔频谱图的计算方法是首先对信号分帧、加窗，进行短时傅里叶变换，然后根据式（4）所示梅尔尺度对频率轴进行映射，将映射后的信号通过梅尔滤波器组，得到每帧都由梅尔频谱表示的梅尔频谱图特征。此外，还可以分帧计算3.2节所述MFCC 系数得到MFCC 时间分布图作为深度学习网络输入。图12 展示了同一段音乐的梅尔频谱图。

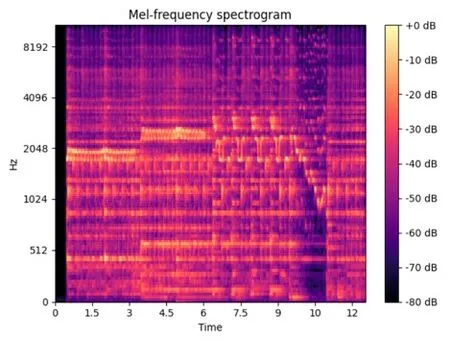
图12 梅尔频谱图

5.3 CQT谱图

CQT是为了解决短时傅里叶变换后频率分辨率固定，不能很好地描述音乐信号的缺陷而提出的时频转换算法。由于音乐中半音和音分的音高值都是按比例确立的，相邻半音的比例为r=，相邻音分之间频率比为c=，因此可以看出在时频转换时，低频需要很高的频率分辨率（长时窗），高频需要较低的频率分辨率（短时窗）。保持频率与频率分辨率比值恒定，比值为Q，可由式（22）计算得出：

其中，fk为第k个频带的中心频率。设频率变化窗口长度为Nk，采样频率为fs，那么两者关系满足：

常数Q变换的公式为：

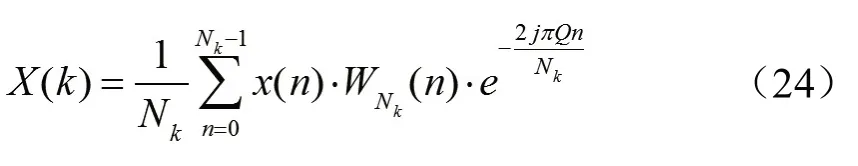
其中，WNK(n)为第k个频带的窗函数。实际使用中，会根据不同的研究对象确定Q。如在音乐信号中，每个倍频程划分的子频带数为12的倍数，此时ΔF=21/12。取每个窗内的CQT频谱，可以得到CQT随时间变化的谱图。图13展示了同一段音乐的CQT谱图。

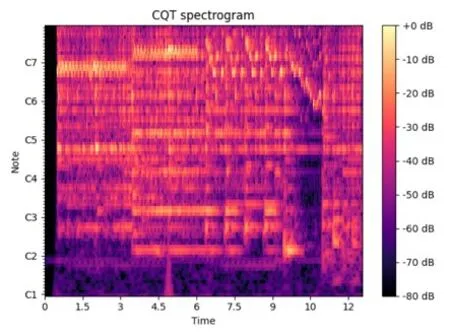
图13 CQT谱图

6 音乐特征的应用

6.1 音乐分类

音乐特征的基础应用是各类音乐分类任务，如乐器分类、音乐风格分类、音乐情感识别等。音乐分类目前主要有两种研究方向，一是手工提取音频特征与各种机器学习分类器结合，研究重点主要有音乐特征的提取与分类器的选择；二是直接将谱图特征作为网络输入，将音乐信号转化为图像表示，利用深度学习网络进行研究。通过音乐特征与人工标注的音乐标签的关联分析，得到音乐分类结果。上个世纪九十年代，World等人［81］就通过提取音频信号的均值、方差特征，利用K近邻算法进行音乐分类。二十一世纪初，Tzanetakis 等人［66］年将节奏、音色和音高等音频底层特征作为特征集合，使用K最近邻算法、高斯混合模型［67］、高斯分类器等算法进行特征集的选取实验，并构建了GTZAN数据集，模型最终取得了61%的分类正确率。该分类标准在搜索领域得到普遍认可，为音乐分类领域奠定了大量的基础；而后甄超等人提出了基于特征重要程度的特征选择算法，选择贡献度高的特征进行分类，取得了81%的分类正确率。随着深度学习技术的发展，越来越多的研究者将目光转向用深度学习技术进行音乐分类，如Choi［70］等人使用梅尔频谱图作为输入特征，使用卷积网络进行音乐标注；Li［71］等人用MFCC系数作为网络输入，使用三个一维卷积层的网络进行音乐分类；Liu［72］等人用音乐色谱图作为输入，使用双向LSTM网络提取音乐情感特征；Choi等人［88］使用一个预训练的convnet特征，即在一个经过训练的卷积网络中激活多个层的特征映射的一个连接的特征向量进行音乐分类取得了86.7%的正确率，Yang等人［89］提取音频STFT谱图特征使用RNN与CNN混合的复合神经网络的音乐分类方法，在GTZAN数据集取得了90.2%的音乐分类正确率等等。

6.2 音乐制作

随着音乐制作数字化、智能化的发展，音频内容分析逐渐应用于音乐制作中，通过使用智能化插件辅助音乐制作，音乐从业人员可以大幅提升工作效率。软件系统通过提取、分析音频特征的方法理解音频内容，自动进行辅助参数设置，如通过自适应增益和均衡参数进行自动混音［73］，以前所未有的方式优化音乐制作。Man 等人［90］为了探究混音师对各音质维度的控制异同点，通过提取音乐动态、空间、频谱共计20维特征分析了8位混音师的多轨音乐混音，分析其方差、趋势或一致性因素，并由此探讨了自动混音的发展前景。ALEX 等人［91］分析了专业混音师制作的共计1501 首作品，通过特征提取和主成分分析得出振幅、亮度、低音和宽度特征对混音质量起重要作用，使用正态分布获得这些特征的一般趋势和误差范围，为智能音乐制作系统的参数化指导。Peeters 等人［92］利用随机森林分类器进行音频特征选择，对音质进行功能分类以实现混音自动分组。Martinez 等人［93］将音乐分为Bass、Guitar、Vocal 和Keys 音轨，提取了1812 维音频特征，使用随机森林、支持向量机和逻辑回归三种机器学习方法最终选择出了6维对音乐混音起重要作用的特征，可用于训练机器学习回归系统预测音频特征值，从而协助音响工程师更好的进行混音。

此外，音频内容分析的引入也提升了生产过程中的创造性，市面已有比较成熟的音频处理产品，例如iZotope［82］将基于音频分析的人工智能技术应用于乐器分离、人声提取等音效处理插件，Zplane Vielklang［83］和声效果器通过分析主唱和和声轨迹来创建具有和声意义的背景和声等等。

6.3 音乐教育

随着计算机技术的发展，互动式智能音乐教学已经随处可见，其目标是帮助教师发现学生表演中存在问题的部分，提供简明易懂的分析，就如何改进给出具体易懂的反馈，并根据学生的错误和总体进步使课程个性化。通常评估一个或多个性能参数，这些参数通常与音准、节奏［75］［76］或音色［77］［78］方面的性能准确性有关。

Seashore早在20世纪30年代就提出了运用技术辅助音乐教育的初步想法。Allvin［74］探索了计算机辅助技术在音乐教室中的潜力，强调了使用音频内容分析技术（如音高检测）可以在音乐表演中进行辅助评价，向学习者提供反馈意见。Nakano等人提出了一个自动系统来评估用户的歌唱技巧［94］，该系统基于提取的基音间隔精度和颤音特征进行训练，评估结果表明，该系统能够以较高的精度将性能分为好或差两类。Mion等人［95］提出了一个基于音频特征的音乐评价系统，通过谱质心、残余能量和每秒音符数等特征提取，对小提琴、长笛等独奏乐器的音乐表情进行分类。Lerch等人［96］提出了一种基于音频特征的音乐成绩自动评估系统，通过完善的和定制设计的音频特征来描述性能，对专业人士给出的评分进行建模和预测。

已经商业化应用的智能音乐辅导系统包括SmartMusic3［84］、Yousician4［85］、Music Prodigy5［86］和SingStar6［87］等。

6.4 音乐传媒与消费

音频信息提取已经被广泛应用到音乐传媒行业中，例如使用基于音频的音乐推荐和播放列表生成系统的流媒体服务，使用对音乐内容的深入了解［50］。除了面向消费者外，使用音乐信息提取还可以自动识别音乐并创建符合公司品牌形象的播放列表［43］。

Shao 等人［97］提出了一种新的动态音乐相似性度量方案，该方案提取了80 维音频特征，基于音乐的声学特征和用户访问模式之间的相关性来进行相似性度量来向用户推荐音乐。Eck等人［98］从音频中提取了MFCC、自相关系数、常数Q 变换谱图等特征从直接MP3文件中预测用户偏好的音乐标签。此外，音频指纹也是一个重要的应用，它用一个小而独特指纹来表示音频文件，其目标是识别特定录音以监管歌曲版权或音乐元数据识别等等。现代音频指纹识别系统的一个简单前身是使用时域包络段作为指纹［99］，用于识别广播中的商业广告。目前，指纹通常是通过STFT谱图特征提取，目前两种主流提取方法，一是以二进制形式对时间和频率上的频带能量变化进行编码［100］，二是识别谱图的显著峰值，并对其相对位置进行编码［101］。

6.5 音乐特征提取工具

大量的开源工具包可以用于提取上述音乐特征，这些工具各具特色，在实际应用中应当根据不同工具的特点来选用，表1列举了常用的音频特征提取工具及其特点。

表1：常见的特征提取工具及特点

7 总 结

特征提取是音乐信号分析中关键的环节，特征的选择和提取方法直接影响到后续音乐信息检索和音乐情感识别算法的性能。良好的音频特征对后续分析的顺利进展奠定了基础，本文对传统音频特征、音乐相关特征和面向深度学习的音频特征做了全面的梳理与总结。音乐信号特征的应用目前主要有基于人工提取特征，使用传统机器学习的研究方法与直接基于音频数据，使用深度学习的研究方法。前者需要研究者有一定的音频与音乐基础背景，在特征选取方面进行探索以选取最优的特征完成任务，后者免去了特征提取、筛选的繁琐步骤，由机器自动理解输入数据。回顾音频信号特征的发展以及当前迫切的研究问题，领域目前主要面临着以下挑战：首先是由于音乐版权或其他限制导致用于训练复杂机器学习系统的数据集难以获取；其次是机器学习系统预测性能以及预测结果的可解释性需要提高；此外，音乐作为一种艺术形式，它本身的音乐语言与乐理概念与人们感知意义和音乐特征的关联性也可能成为未来的研究方向。