复数阶累加的灰色系统模型

吴正鹏，陈见柯，柴剑平

(中国传媒大学数据科学与智能媒体学院，北京 100024)

1 介绍

自古以来，人们就关注着基于现有记录的对即将到来事情的预测。随着科学技术的发展，人们现在生活在一个“大数据”时代。尽管如此，马鑫最近发布的一篇论文声称，基于小样本的高效学习仍有可能训练智能AI，大数据不应该是高效AI 的唯一途径[12]。此外，由于这些高速的发展，自然会出现新的现象和问题(例如，二氧化碳排放标准、网络突发舆论、能源消耗等)，应该有快速且高效的应急设施。就像可怕的自然灾害一样，相关的静态结果可能是不完整的，或者是不充分的。因此，关于小信息量的预测问题仍然存在很多情况。

20 世纪80 年代，邓聚龙提出了灰色系统理论[3,4]，为解决信息贫乏情况下的小样本预测问题提供了一种新的方法。GM(1,1)模型，即一元一阶灰色模型，在整个理论中起着至关重要的作用。邓还给出了原始GM(1,1)模型的几种不同形式。此后，许多学者继续为这一理论发展不同的模型[9,10]。到目前为止，在理论修改（例如，寻找更好的模拟和预测结果[25]）和优化算法（灰狼优化、粒子群优化[13]）方面，朝着这个方向取得了许多进展。对原始GM(1,1)模型进行了不同形式的修正，以适应不同的预测情况，例如抗拉强度[16]、二氧化碳排放[21]、冰塞灾害[11]等的间接度量。对于给定的时间序列，为了在未来的预测中引入定性分析（即强度或弱化Γ，刘思峰提出了（包括加强和弱化）缓冲算子的思想[10]。这些算子满足3个公理：不动点、充分利用信息、解析性和正规性。许多学者开发了这类工具，将缓冲运算符应用于不同类型的模型预测[24]。

莱布尼茨提出的分数阶微积分思想对灰色系统也有很大的影响。吴立峰、刘思峰等人[23]首次考虑了分数阶累加的灰色模型。该公式将整数阶累加的经典灰色模型推广到分数阶灰色模型。这一创新在理论和实践上都对灰色系统进行了巨大的改进。从那时起，分数阶累加成为灰色系统中一种流行而有效的工具[14,22]。为了在旧信息和新信息之间保持平衡，李冲、英杰、昂英杰等人提出了自己的观点，开发了新的序列运算符[8]。

目前，Matlab 软件已取代Visual C#，成为大多数研究灰色系统的学者的主要计算机编程工具，他们大量使用Matlab 语言中嵌入的伽马函数。但Matlab 语言中插入的伽马函数不能直接编译出一般的复数值（例如Γ(1+i)）。本文利用幂零矩阵和泰勒级数，给出了复数累加的灰色模型的一种新的、直接的表述。由于复数域X 是代数闭域，也是拓扑完全域[7]，这个公式将经典的整数累加的灰色模型[3]和分数累加的灰色模型[23]推广到其最一般的形式。正如我们将看到的，复杂积累的灰色模型将会得到更好的模拟结果和预测结果。

本文组织如下。第二节讨论了经典的整数（分数）阶累加生成算子和一阶一元GM(1,1)微分方程的灰色模型。我们将分数累加生成运算符(因此，自动包含整数的情况)推广到复数累加生成运算符。考虑所有复数累加生成算子的集合，我们将证明该集合具有一维复李群结构。在第三节中，我们建立了复数累加的灰色模型（对于某些z∈X，用CAGMz(1,1)表示），并确定了它的解。由于我们可以将实数P 看作X 的一维子空间，即我们在一个更大的区域上工作，自然会期望CAGMz(1,1)模型产生比类似模型更低的平均绝对百分比误差MAPE 和均方根百分比误差RMSPE（其定义将在稍后给出）。在第四节中，通过几个具体的例子讨论了CAGMz(1,1)模型相对于类似模型的优势。第五节介绍了对本研究的一些期望。

2 复数累加生成算子

设X(0)= (x(0)1,x(0)2,…x(0)n)是原始数据序列。对于1≤k≤n，设x(0)k∈X为时间k时的值，数据序列是列序列还是行序列，只是转置不同而已。为方便起见，我们将在以下结构中使用行序列。设n=dim(X)是行数据序列空间的维数。对于实际问题和具体问题，应该注意到数据序列中的条目是铁的生产量、用电量、某一地区的GDP、二氧化碳排放量等，所以一般地这些x(0)i∈Θ。但我们想以最一般的形式来构建这个行动。

2.1 传统累加生成算子与GM(1,1)模型

一阶累加生成算子和一阶逆累加生成算子在灰色系统理论中占有重要地位。基于这些运算，GM(1,1)模型是灰色系统理论中的一个基本模型[9,10]。

定义1设X(0)= (x(0)1,x(0)2,…x(0)n)是原始数据序列。设X(1)= (x(1)1,x(1)2,…x(1)n)是数据序列，如果我们对X(0)应用一阶累加生成算子，X(0)的坐标由下式给出

X(0)的一阶逆累加生成算子表示为X(-1)，其坐标由下式给出

很容易验证一阶累加生成算子和一阶逆累加生成算子是对数据序列的逆运算。

对于2 ≤k≤n，设w(1)k=。那么方程

称为GM(1,1)模型的原始形式。a,b为GM(1,1)模型的参数。a,b的最小二乘估计由下式给出

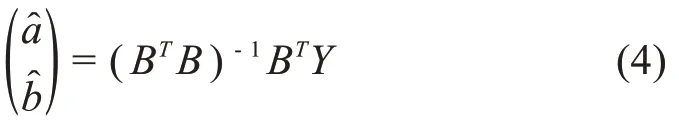
其中

在初始值x(1)1=x(0)1的情况下，白化方程

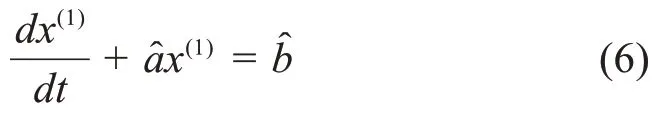
的时间响应序列由下式给出

其中1≤k≤n。最后，如果对序列(x(1)1,x(1)2,…x(1)n)应用一阶逆累加生成算子，则模拟序列满足

其中2≤k≤n.

2.2 复数累加生成算子

定义2[23]设原非负序列X(0)的r(r∈P>0) 阶累加生成算子为X(r)。然后

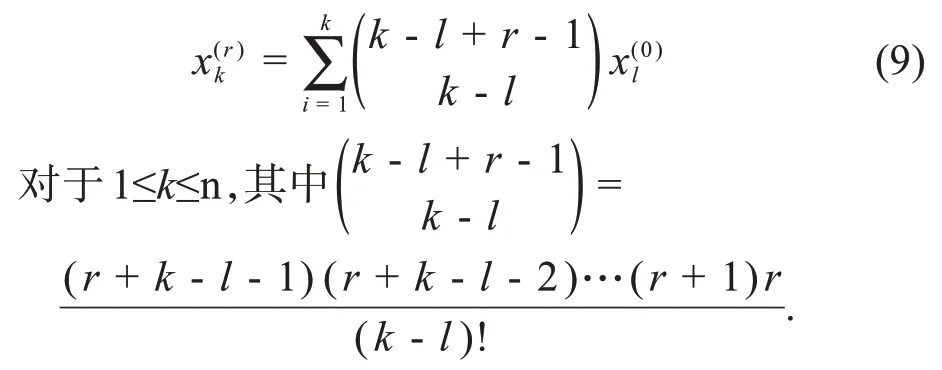
与传统的整数阶累加灰色模型相比，分数阶累加灰色模型在实际应用中（无论是理论基础还是模型仿真）都会得到更好的结果。分数阶灰色模型在许多不同的场合得到了广泛的应用。许多学者提出了建立这一理论的新方法[13,14,15]。

为了将现有的理论推广到复累加生成算子的情形，我们将使用代数公式[6,7]。

设x是幂零不定式，使得xn= 0，则显然

分别设f(x) =(1+x+x2+ …+xn-1)和g(x) =(1-x).设

即I是n×n单位矩阵，E1是幂零矩阵。对于1≤k≤n，设Ek:=Ek1.直接计算如下

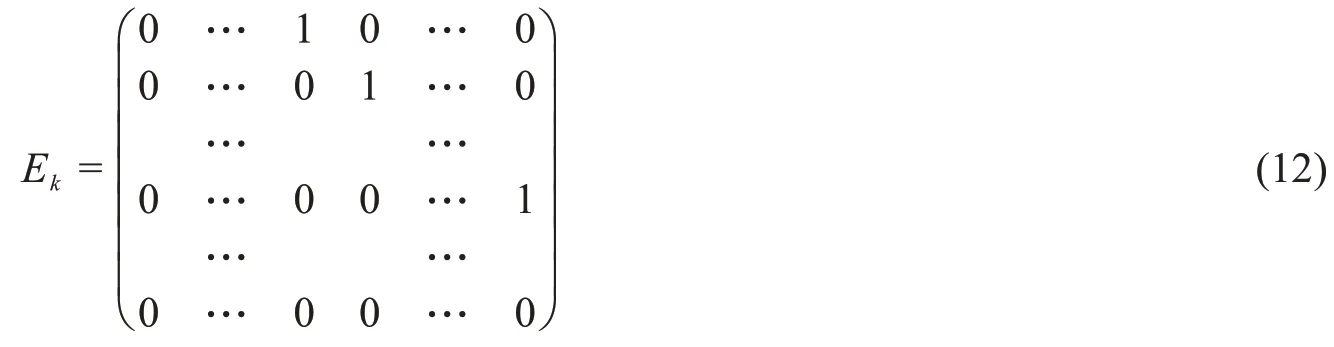
En=En1=On×n，其中On×n为零矩阵。然后，对于一阶累加生成算子A和一阶逆累加生成算子A-1，存在

或者等价地f(E1)g(E1)=I。归纳地，第二累加生成算子A2等价于f2(E1)。通过为z∈X设置A(z):=f z(E1)，我们将给出以下定义：

定义3设X(0)为原始数据序列并且z∈X，则第z次复数累加生成算子由A(z)定义。如果我们用X(z)表示第z个累加数据序列，那么

其中符号· 表示通常意义上的矩阵乘法。

定理1所有z∈X 的第z个累加生成算子集构成一个1维交换加性李群，它与X同构。

3 复累加的灰色模型

设X(0)=是原始数据序列，z∈X使得Im(z) ≠0 是复数。如上所述，对于1≤k≤n，一般地∈P。设是第z个复数累加生成序列。在第z次复数累加生成运算 之 后，对 于 1≤k≤n，有∈X。 设W(0)=(w(0)2,…,w(0)n)是X(z)的连续邻域序列的平均生成，即对于2≤k≤n，w(z)k=.我们给出以下定义：

定义3 对于2≤k≤n，方程式

将被称为第z个复数累加生成运算的灰色模型的原始形式，其将被表示为CAGMz(1,1)。常数a称为灰色发展系数，b称为灰色控制参数。

注1如果z= 1，这是经典的GM(1,1)模型。对于复累加情况的灰色系统模型，应该注意到这两个参数，即a和b，一般都是复数。

CAGMz(1,1)模型的普通最小二乘估计序列满足

其中

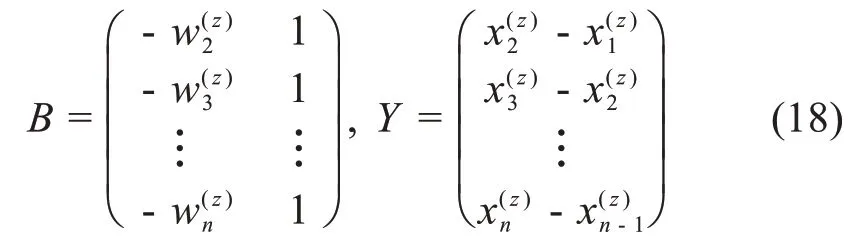
定义4设B,Y,a,b如上所述，微分方程

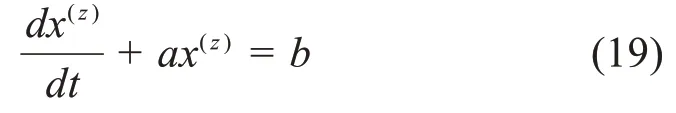
将称为CAGMz(1,1)模型的白化方程。

在初始值x(z)1=x(0)1的情况下，很容易得出时间响应序列具有以下形式

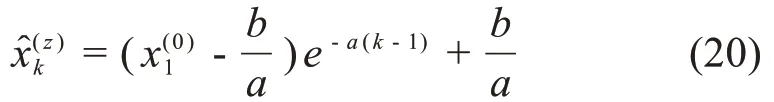
对 于 2≤k≤n.最后，如果我们对序列应用第(-z)次复数累加生成A(-z)(或者等价地，第z次复数累加生成操作的逆运算)，我们将得到模拟序列，即

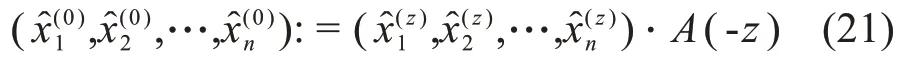
设X(0)=是原始数据序列，我们可以假设x(0)k=αk+iβk，其中αk,βk∈P.将CAGMz(1,1)模型应用于X(0)，并设为仿真数据序列(0)=。一般地，由于(0)k∈X，我们可以假设̂，其中，设ε=(ε1,ε2,…,εn)是剩余序列，则

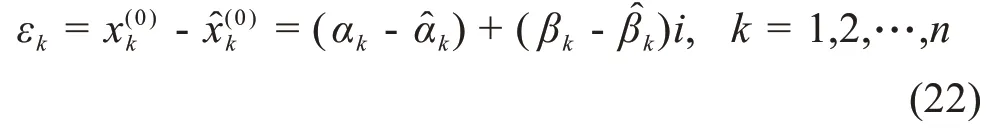
为了对CAGMz(1,1)进行误差分析，同时对已有的理论进行推广，我们将利用复数的模来对其进行误差分析。更准确地说，设Δ =(Δ1,Δ2,…,Δn)为相对误差序列，则

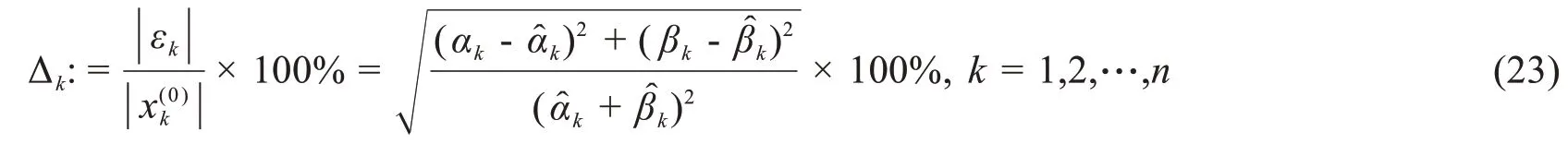
综上所述，给定一个原始数据序列X(0)=(x(0)1,x(0)2,…x(0)n)，建立第z个CAGMz(1,1)模型的步骤如下：

步骤1：选择复数z∈X，使得Im(z) ≠0，并计算第z个累加生成数据序列，即X(z)=X(0)·A(z)；

步骤2：计算X(z)的连续邻域序列W(z)的平均生成量；

步骤3：通过对复矩阵的最小二乘估计，给出了参数a,b的估计，即=(BHB)-1BHY，其中B,Y由方程(x(z)k-x(z)k-1)+aw(z)k=b给出，BH为B的复共轭转置矩阵；

步骤5：通过经由A(-z)将第(-z)复数累加生成运算(第z个累加生成运算的逆运算)应用于(z)来计算模拟值(0)，即(0):=(z)·A(-z)；

步骤6：计算残差数据序列ε 和相对误差数据序列Δ，进行误差分析。

对于具体问题，通过选择一个有理数作为累加生成顺序，即z∈Θ，则A(z)中累加生成算子的条目和模拟值(0)都是有理数，即A(z)i,j∈Θ，1≤i,j≤n和，1≤k≤n。由于大多数预测模型的模拟值仍为正有理数，即取模数与模拟值相同，即，1≤k≤n。由于累加生成阶数可以从所有复数中选择，因此可以认为CAGM模型是分数累加灰色预测模型的推广。

4 个案研究

案例1

我们考虑的第一个例子是沥青混合料，它广泛应用于道路建设中。在一定的条件下(例如，激振频率、材料温度等)，沥青混合料的变形缓慢(粘性)，一旦变形力消失(弹性)，沥青及其混合料的这种性质称为粘弹性。沥青混合料的复模量E*(=E′+iE″，一个复数)由两部分组成，其中E′表示混合料的储能能力(弹性行为)，E″表示耗能能力(粘性行为)。动态模量E*被定义为模量[27]。

早期对E*的研究主要集中在动态模量主曲线[19]，忽略了E*的θ相位角，而后者也是沥青和沥青混合料的一个重要影响因素，例如，最近的一项研究发现，相位角是区分沥青混合料噪声特性的一个很好的实验室参数[1]。近年来，研究人员试图开发相角的主曲线[2,26]，曾鸣等人提出的广义CAM 模型由复模量主曲线、相角主曲线[28]组成。Venudharan 等人发展了储能模量和损耗模量的预测模型[17]。可以同时考虑动模量E*和相位角θ。表1和表2列出了AC-20C 70#型沥青混合料的实验值[2]。

表1 AC-20C 70#沥青混合料的动模量(MPa)

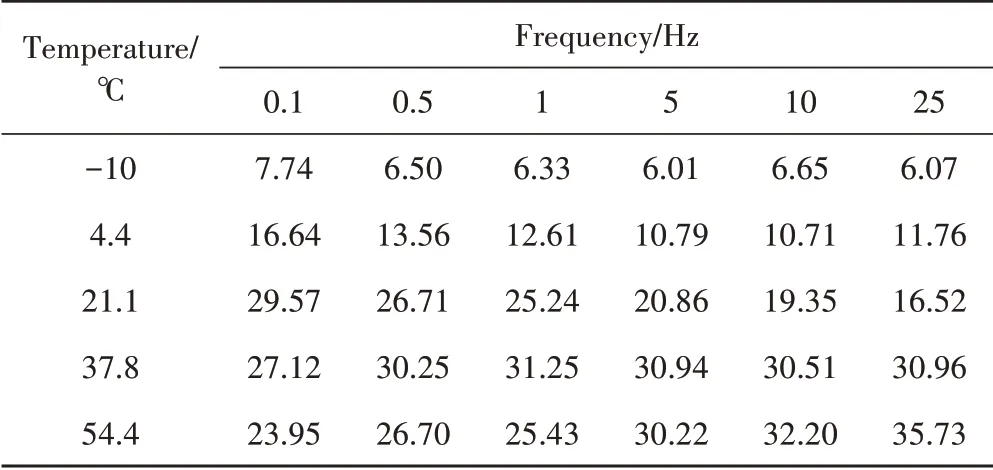
表2 AC-20C 70#沥青混合料的相角(°)

通过欧拉公式eiθ= cosθ+isinθ，任意复数z=a+bi可以重写为z=|z|·eiθ，其中是模数，θ是相位角(tanθ=，a≠0)。以温度4.4°C 为例，原始复数数据序列(取决于频率)为

作为比较，我们选择3 个累积生成阶z= 0.9 + 0.12i，z= 1 和z= 0.5 来构建CAGMz(1,1)模型。第0.9 +0.12i个累加生成算子A(0.9 + 0.12i)为

z= 1和z= 0.5的累积生成算子与一阶和分数阶的累积生成算子相同。

应用这些运算符，我们将得到第0.9+0.12i个累加生成数据序列

一阶累加生成数据序列为

0.5阶累加生成数据序列为

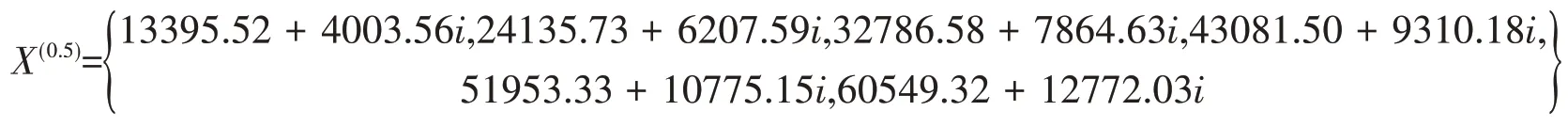
当z= 0.9 + 0.12i时，a= 0.074 - 0.025i，b= 14211.04 + 4390.87i，时间响应方程(对于k= 2,3,…,6)

当z= 1时，a= -0.098+ 0.007i，b= 15558.57+3579.62i，时间响应方程(对于k= 2,3,…,6)

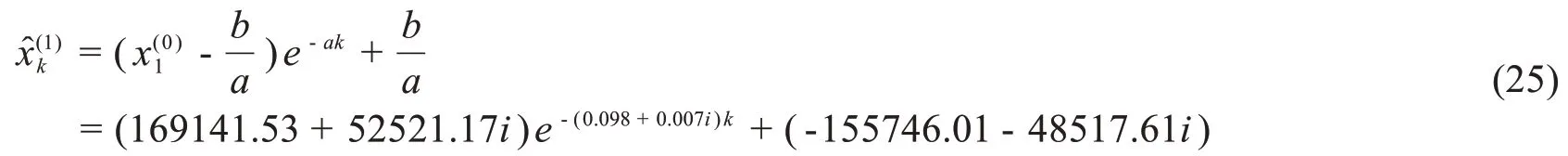
当z= 0.5时，a= 0.043- 0.0087i，b= 11072.99+2088.93i，时间响应方程(对于k= 2,3,…,6)

由于原始数据序列X0和模拟数据序列0都是复数，为了进行误差分析，我们将使用复数的模来进行误差分析。以第(0.9 + 0.12i)次复数累加的相对误差Δ6为例，

表3列出了复模量数据序列CAGMz(1,1)模型的三种不同的模拟值和误差。

表3 CAGMz(1,1)模型的模拟值和误差

案例2

下面的例子描述了1994-2000年间美国的旅游需求[18,22]。基于这些实际值建立了四个不同的灰色模型(我们考虑了CAGMz(1,1)模型的三个不同参数)，并以来年(2001年，样本外)为预测对象。所有结果都列在表4中。

如上所述，承认了关于预测的MAPE 建模的MAPE。为了使预测MAPE 取一个较低的值，可以取z1= 1.232 - 0.506i，CAGMz1(1,1) 模 型 给 出 的 预 测MAPE最低(≈0.00116%)。对于这种情况，虽然模型的MAPE 高于其他三种模型，但这两种MAPE 的总和仍然很低(≈3.13%，而GM1.2(1,1)模型为3.7%)。设置z2=1.176-0.13i，则建模的MAPE 为1.33%，这是表4所列结果中的最低值。出于另一个考虑，我们可以选择z3= 1.23- 0.5i，这仍然是一个更好的模拟。

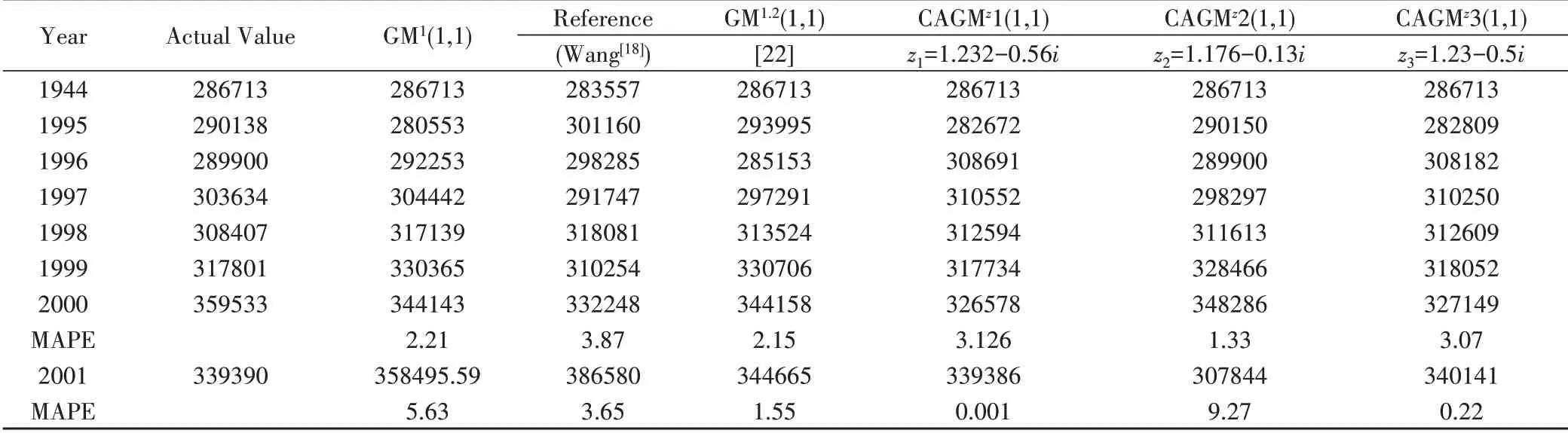
表4 四种不同模型的拟合值和MAPE

5 结论

本文将整数、分数累加生成算子推广到复数累加生成算子。结合所有的复数累加生成算子，我们得到了一个自然的一维可加复李群结构，它与X同构。与以前关于实数(整数或有理数)的讨论相比，我们的工作是在整个复平面上进行的。复数阶累加生成算子可以同时调整新旧信息之间、实部和虚部之间的权重，可以得到更好的仿真和预测结果。通过几个实例，讨论了复数累加灰色模型与常用方法相比的优越性。

为了进一步研究，我们将列出几个可能的问题：

(1) 灰色理论中的一些技术，例如光滑比ρ、区间灰数、灰色关联算子等都依赖于P中的阶关系，但复数域X不存在阶关系。如何将这种技术扩展到复数数据序列的情况；

(2) 将分数阶微积分的思想引入灰色理论，提出了分数阶累加生成算子。根据我们的构造，将累加生成阶推广到复数，人们可能会问：是否存在复数阶演算？

(3) 寻找涉及复杂数据序列的复杂灰色模型的应用，例如复信号分析、沥青及其混合料的粘弹性等。