车载式施药机的伺服特性分析
贾功流
(安徽省康禾农林病虫害综合防治有限公司,合肥 230000)
0 引言
在植物生长中,病虫害是导致作物产量降低的主要原因之一,我国病虫害发生面积广、农药使用量居高不下。在施药装备中,系统的伺服控制特性起着关键作用,它是施药机械精准喷施、提高农药利用率的决定性部件。但是,从国内外施药机械发展的趋势来看,手动控制及粗放控制的伺服系统仍占着主流,因此,为提升施药系统的控制水平,使其喷施功能特性更适应用户需求是十分必要的。
本文针对车载式施药系统的伺服控制单元,对施药机驱动单元的控制系统进行了深入分析,并对电流环、速度环进行了逐一仿真,研究证明,控制误差小,精度高。
1 伺服控制系统
在伺服系统中,起主要作用的部分是放大电路、伺服电机和传动装置。伺服系统工作时,控制器的输出信号,通过放大电路处理,作用于伺服电动机,电动机输出转矩再通过传动装置,驱动负载运动完成设定转动,控制回路如图1所示。
2 电流环设计
首先建立系统的等效模型,在模型的基础上根据系统要求的性能指标对系统的电流闭环、速度闭环、位置闭环进行了设计与仿真。电流环数学模型如图2所示。
根据单位阶跃BODE图3可以看出,校正后电流环的上升时间tr=0.401 ms,超调量8.86%,开环相位裕度为 74.8°,系统是稳定的。
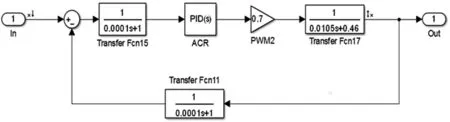
图2 电流环仿真框图
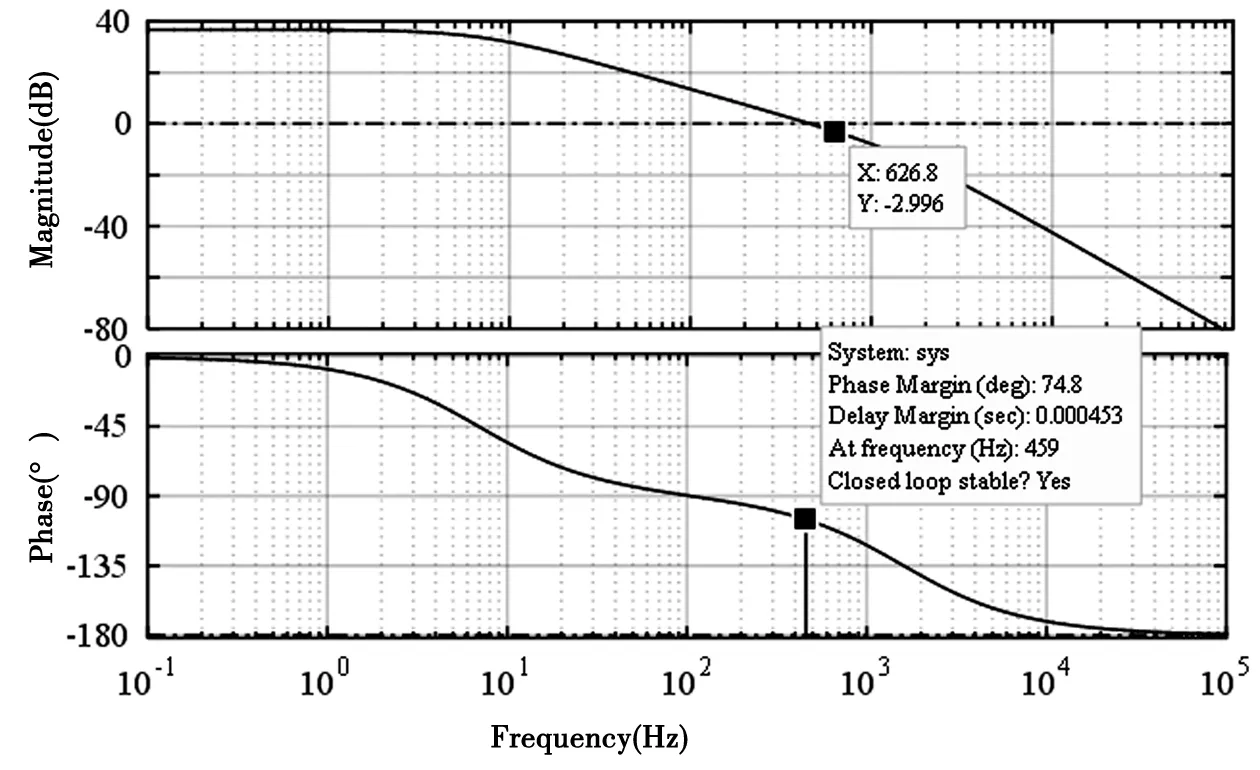
图3 电流环BODE图
3 速度环设计
在电流环的基础构建速度环,建立速度环仿真模型如图4所示。
通过位置环阶跃响应可以看出,速度环的阶跃响应上升时间tr=0.017 s。根据方位速度环BODE(图5所示),相角裕度为88.9°,因此速度环是稳定的。
4 精度分析
利用保精度角速度和保精度角加速度指标计算等效正弦信号,并以此作为伺服控制系统的跟踪精度检验信号
指标要求保精度最大速度为6 rad·s-1,最大加速度为3 rad·s-2根据保精度最大速度和最大加速度的要求,可设计正弦波角位置指令满足上述最大加速度和最大速度的要求。
根据方位保精度最大速度为6 rad·s-1,最大加速度为3 rad·s-2,可计算出满足此要求的角位置指令
Azc=12sin(0.5t)
将位置输入带入模型中,得出误差信号。由图6可以看出,跟踪误差的峰值为0.25°;稳态误差峰值为0.17°;均方根误差为0.121 1°。加入前馈控制后,调节前馈控制器参数,可使跟踪误差调节到0.028 9°,最终可在0.03°以下,见图7,满足精度要求。
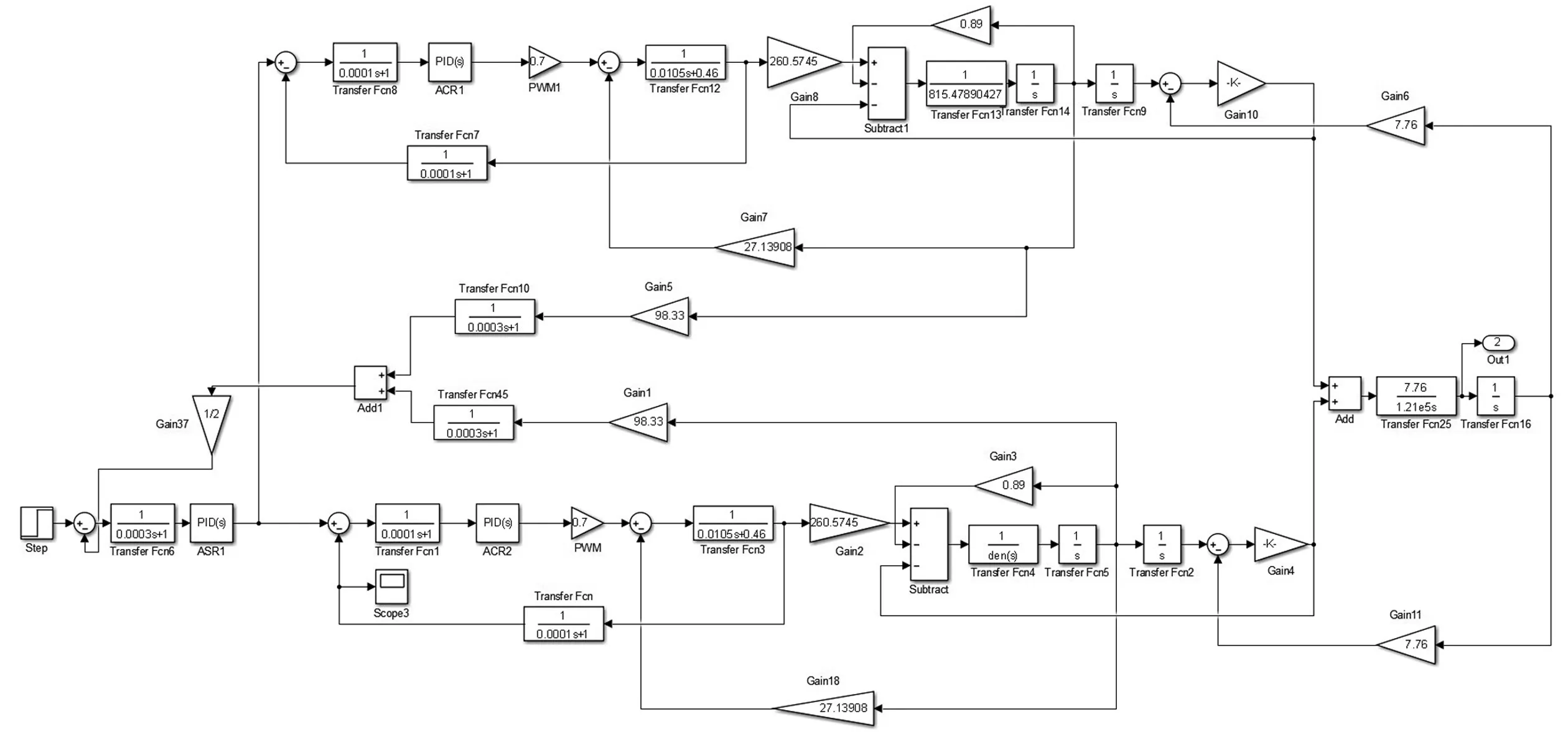
图4 速度环仿真框图
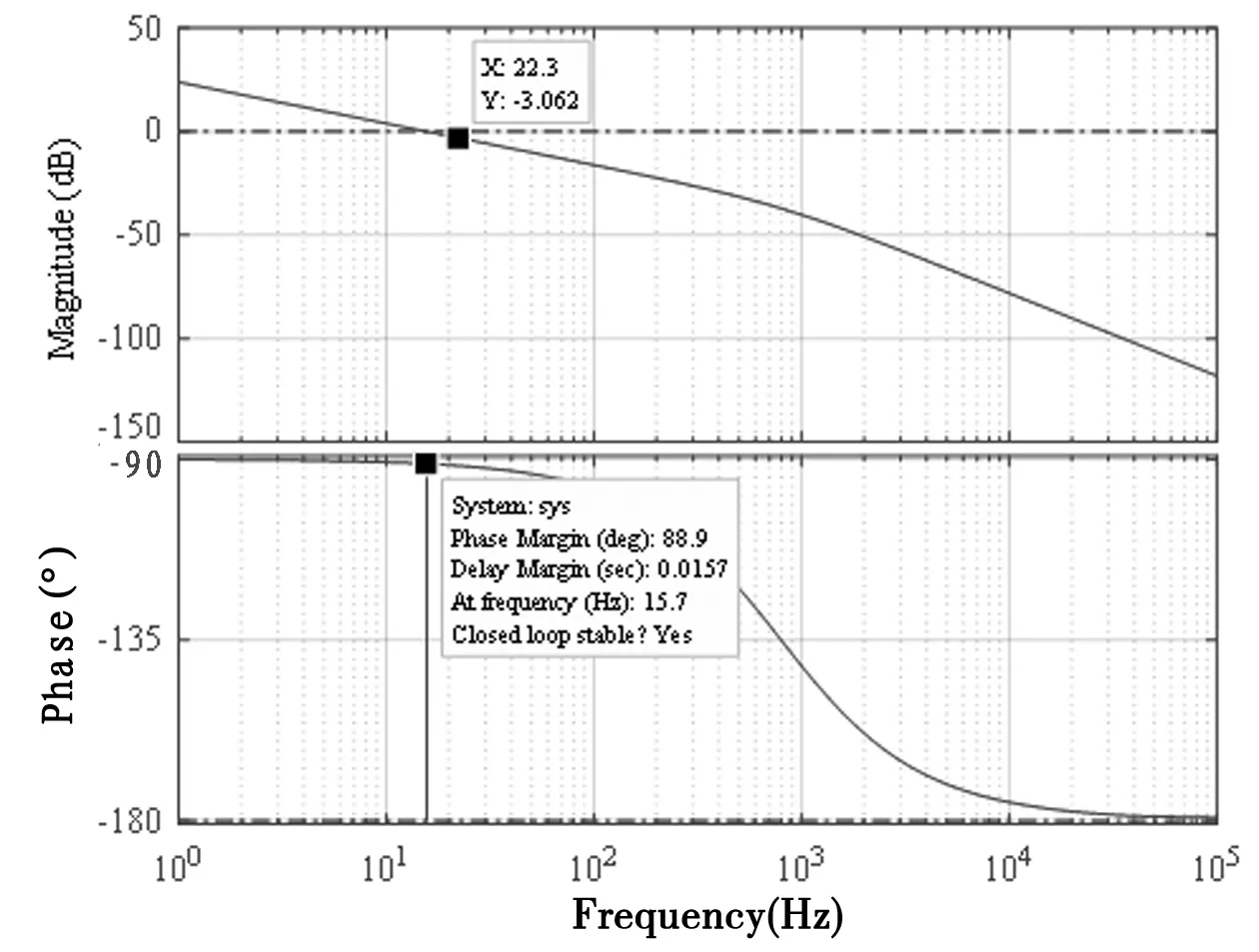
图5 位置环BODE图
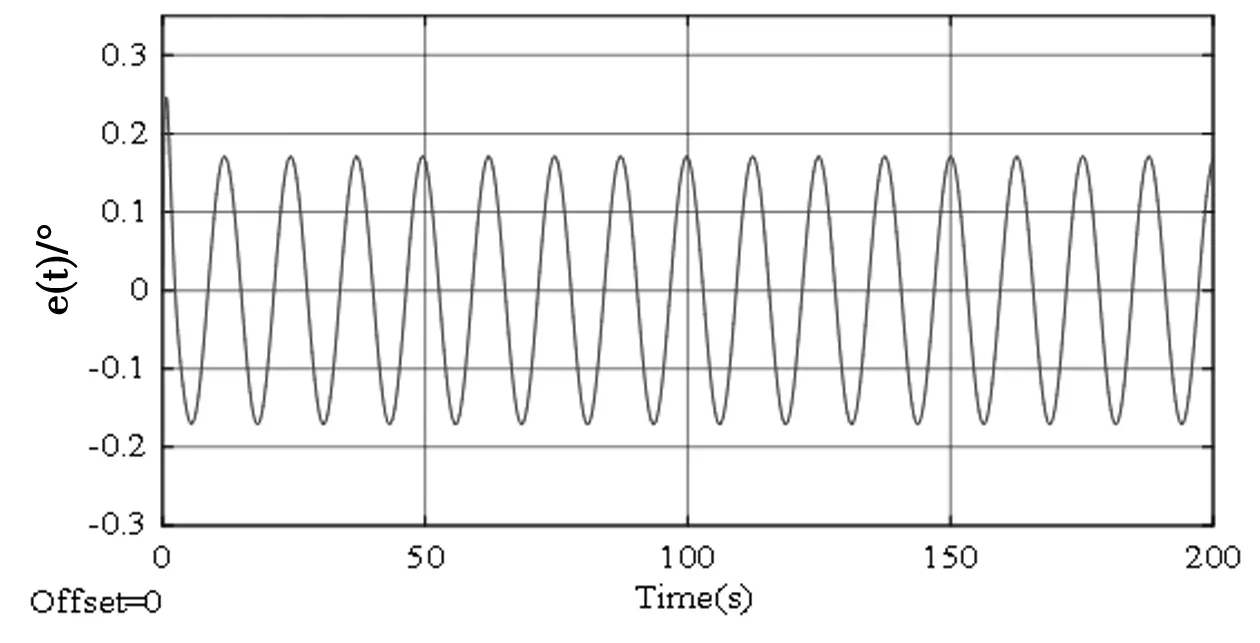
图6 正弦信号下的跟踪误差
在相同工况下,对有无速度前馈的位置特性进行了仿真对比,通过对比可以看出,在不带有速度前馈时,跟踪误差达到0.25°,加上速度前馈后,跟踪误差仅0.028 9°,大大提高了位置跟踪精度,使施药机的伺服特性得以大幅度提升,有利于施药系统快速精准的达到指定位置,说明该方案更能发挥速度环的优势。
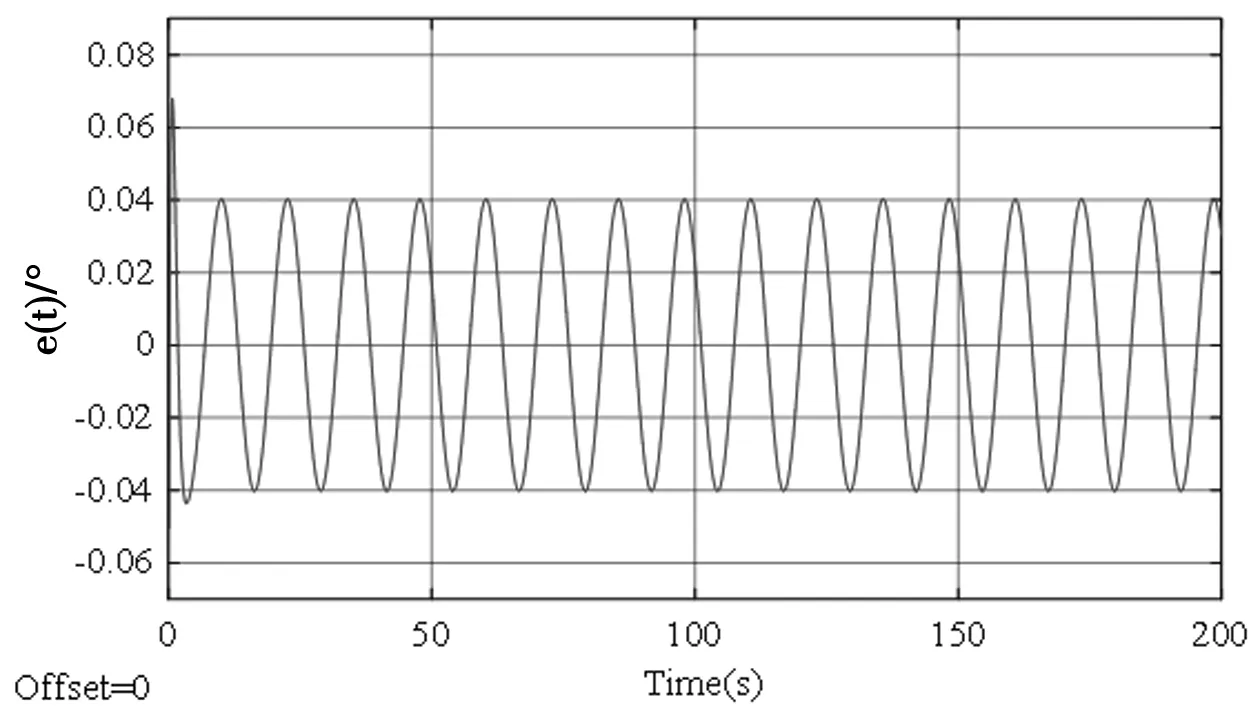
图7 正弦信号加入前馈的跟踪误差
5 结语
本文描述了车载式施药机控制系统的组成。对系统的电流闭环、速度闭环进行了系统建模设计与Simulink仿真。通过阶跃信号下的BODE图仿真,获得了电流环及速度环的伺服特性。根据指标要求进行了位置跟踪仿真,对比了无前馈和有前馈下的误差分析。该系统控制简单,在车载式施药机的伺服三环控制中具有应用价值。

