储层地震物理模拟的震源指向性及介质非均质性影响分析

司文朋, 杨勤勇, 邢廷栋, 薛诗桂

1 中国石化石油物探技术研究院， 南京 211103 2 中国石化地球物理重点实验室， 南京 211103

0 引言

地震物理模拟技术是将野外的地质构造或地质体按照一定的比例制作成物理模拟，利用压电陶瓷换能器激发和接收在物理模型内传播的超声波，实现对地震波在实际介质中传播的模拟，从而对地震波传播规律及特征开展研究工作.物理模拟作为一种重要的地震波传播正演手段，与数值模拟相比具有结果更具真实性、不受计算方法和假设条件限制等优点.近年来，随着地震物理模拟实验数据高速采集系统等技术创新，地震物理模拟技术在地震波传播基本规律、野外地震勘探方法验证、观测系统验证(Di et al., 2008)等方面有诸多应用.比较典型的领域如碳酸盐岩缝洞型储层“串珠状”地震反射响应特征(魏建新等，2008; 赵群等，2010; 李凡异等，2016)及储层真实体积估算(曲寿利等，2012; 李倩等, 2014)、裂缝型储层的地震波传播各向异性特征(Yin et al., 2011; Mahmoudian et al., 2015)及多尺度裂缝预测方法验证(Wang et al., 2018)、复杂构造地质体地震波响应特征(Wu et al., 2014)等方面，基于物理模型实验数据均取得了大量有价值的地震响应规律结论，为实际生产提供了基础认识和参考.另外，也有学者利用物理模拟技术在地震槽波传播特征(皮娇龙等，2018)、砂体刻画(Sherlock et al., 2003)、储层流体识别(Wandler et al., 2007; Wang et al., 2013; 徐超等，2014)、近地表衰减模拟(高峰等，2018)等方面进行了尝试性的研究工作.

对于构造型地质目标的地震物理模拟，多是利用环氧树脂、硅橡胶、滑石粉等有机或无机均质材料构建模型，针对反射波走时等几何地震学特征规律开展研究.将不同类型的含油气储层作为模拟目标时，则需要考虑能否得到与野外实际资料类似的振幅、衰减、频率等动力学传播特征.这就要求储层地震物理模拟在满足几何相似性的准则下，还需要进一步满足物理规律的相似性，例如油气饱和度引起的纵波及横波速度、衰减变化规律的相似性(司文朋等，2017).

在储层地震物理模拟中，为了提高实验数据的准确性和可信性，首先要消除模拟方法本身对实验数据的影响.由于地震物理模拟中使用的模拟震源(换能器)具有振幅指向性，即激发的子波能量随着入射角度的增大而急剧减小，会影响到实验数据的振幅特征，尤其会对振幅随入射角变化的AVO特征产生严重干扰，因此需要格外重视并加以准确校正.另外，在储层地震物理模型构建中，通常采用有机或无机胶胶结平均直径约0.01 mm至5 mm的石英砂等颗粒介质作为模拟储层(刘东方等，2015；裴宇翀等，2016)，而颗粒介质在地震物理模拟超声频段下具有尺度非均质性，同样会对实验数据产生影响.针对以上两个问题，本文对震源指向性及模拟介质非均质性对实验数据的影响开展了高精度实验测试，基于测试结果形成了模拟数据振幅补偿方法，并明确了储层模拟的等效介质条件，为不同类型储层的地震物理模拟准确实验数据获取提供了支撑.

1 震源指向性影响

1.1 指向性实验测试

超声波换能器在地震物理模拟中作为模拟震源，其辐射场具有随着开角(与法向出射的夹角，范围为-90°到90°)增大而能量急剧减小的非球面特征，称之为震源指向性.这与野外实际地震勘探中炸药震源及可控震源、海上气枪震源的球面辐射特征具有明显差异，因此需要加以校正才能保证地震物理模拟实验数据的可信性.针对换能器指向性的理论计算，已经有学者开展过一定的研究(Tang et al., 1990; Maike et al., 2009).但由于影响换能器性能的参数众多，如压电晶体的大小、换能器的结构以及压电晶体的类型等，理论计算往往与实际情况存在较大差异.为了获取准确的换能器指向性，还是需要采用实验测试的结果.以往的测试多采用水中测试或者固体测试的方法(Tang et al., 1992)，测试原理是用水或者半球状均匀固体作为超声波传播介质，保持激发换能器位置固定，在水中或者沿半球状固体球面移动接收换能器，在不同的角度上接收具有相同传播距离的超声波的波形，提取振幅即得到换能器指向性.以往方法的缺点是接收换能器同样具有指向性，在非0°开角时接收到的振幅势必受到影响，而固体测试中接收换能器每次移动后的耦合程度也会影响到测试振幅值的精度.

由于激光测振采用光学干涉作为测量原理，在检测振动时没有指向性限制，同时检测不受距离和耦合影响，能够极大提高测量精度，因此本文采取了非接触式激光测振新方法构建了换能器指向性实验测试平台，如图1所示.测试装置主要包括：超声放大器、超声换能器、直径10 cm半球状铝块、激光测振仪和计算机组成.测试具体过程为：(1)将换能器固定在半球状铝块底部圆面的中心处，换能器与铝块之前涂抹适量耦合剂确保耦合良好，以减少空气阻碍超声波传入铝块;(2)换能器连接超声放大器，根据换能器主频调节放大器增益等参数;(3)利用激光测振仪在半球状铝块过球心的半圆弧面上-90°至90°开角范围内以5°为间隔逐点移动测量，得到不同开角上的换能器超声波振幅值;(4)多次测量求取平均值，得到均一化之后的指向性结果.

图1 换能器指向性激光测振实验构建Fig.1 Set up of transducer directivity measurement by laser vibration method

通过以上步骤，得到不同开角上的换能器超声波波形，如图2a所示.提取振幅值后进行均一化处理，得到图2b显示的指向性结果.可见在开角从0°增大到60°时振幅急剧的减小，而开角大于60°后几乎没有能量.

1.2 数据校正

在测试得到归一化的换能器指向性后，首先计算各个开角αi上测试值与数值1的比值k(αi)，随后计算其倒数1/k(αi)即为各开角上的补偿系数.对于地震物理模型实验数据，首先进行常规处理，抽取得到AVA(振幅随入射角)道集.对于单界面的物理模型，可认为入射角与换能器开角相同，可直接对AVA道集的振幅值进行加权补偿.对于多界面的物理模型，在首个界面处可认为入射角与开角相同，其他界面处则需要根据射线追踪计算出入射角与透射角的关系后，再依次进行补偿.图3为一个单界面物理模型实验数据的AVO特征在振幅补偿前后的对比，图中理论计算结果是利用Zoeppritz方程的近似公式(Shuey, 1985)计算得到.可以看出，经过补偿后的振幅有了明显增加，尤其是大入射角处的振幅值，补偿后的物理模型实验数据AVO特征非常接近理论计算结果.因此，振幅指向性补偿保障了利用物理模拟进行不同类型储层AVO特征研究的可行性及数据准确性.

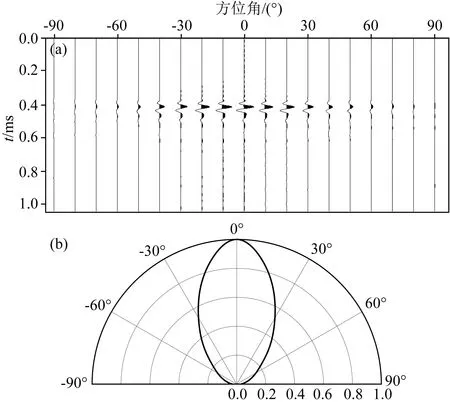
图2 换能器指向性测试(a) 道集记录; (b) 均一化结果.Fig.2 Measurement of transducer directivity(a) Gathers; (b) Homogenization result.

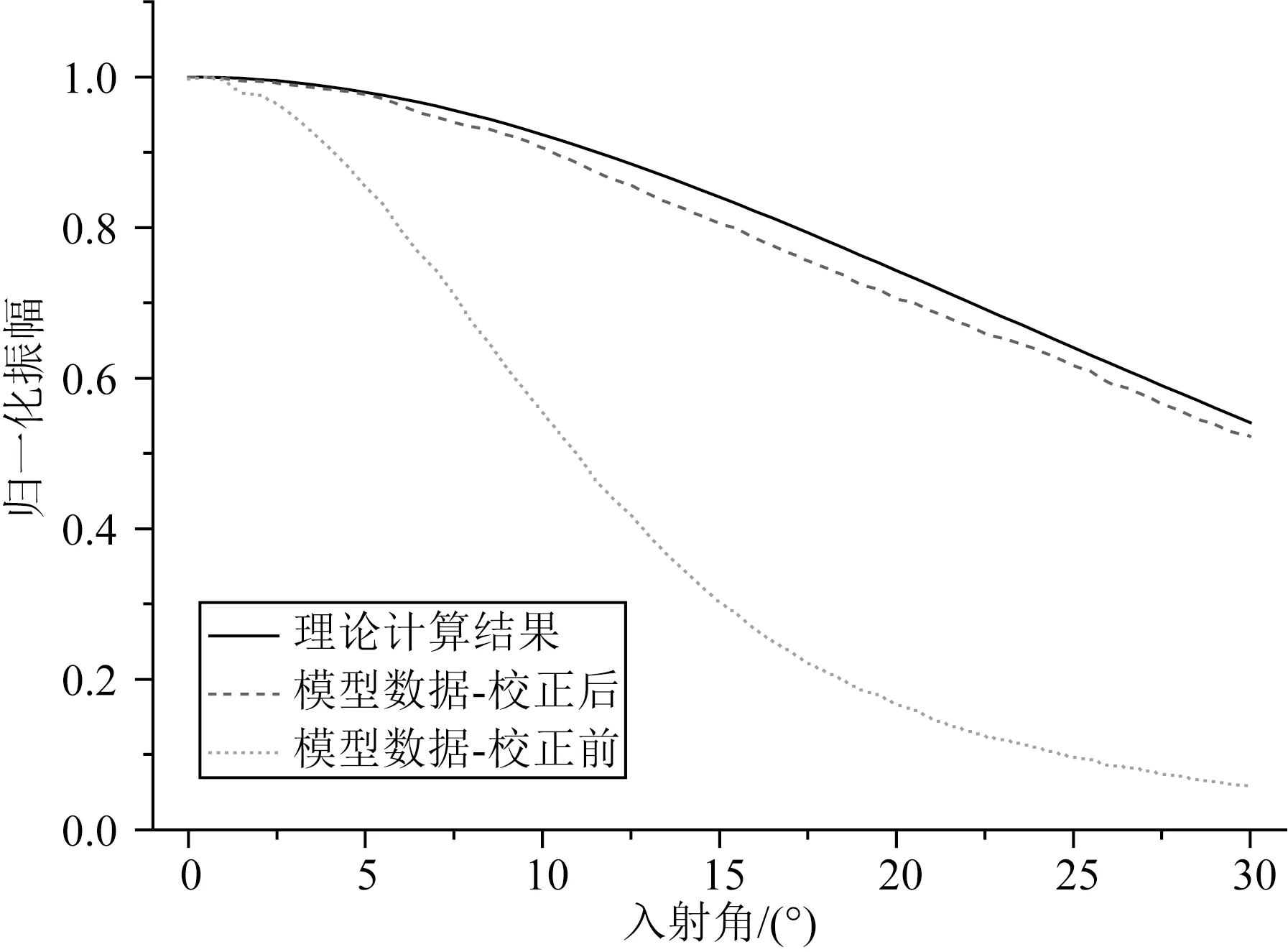
图3 物理模型实验数据校正前后AVO特征对比Fig.3 AVO characteristics comparison before and after physical model data correction

2 介质非均质性影响

尺度非均质性对波传播的速度及能量特征具有重要影响(Yin et al., 1995； Sivaji et al., 2002; Robert et al., 2013; 未晛等，2019).地震物理模拟技术从均匀介质的构造模拟发展到非均质介质的储层模拟，模型介质中颗粒材料的尺度非均质性对实验数据有效波的影响，也是不可忽视的问题.通过制作具有不同平均尺度的非均质物理模型样品，在物理模拟超声频段下测量了模型纵波速度及干扰波/有效波能量比，明确了非均质性对实验数据的影响规律.

2.1 实验测试

2.1.1 样品准备

将具有不同尺度(平均直径)的石英砂嵌入进低速均质介质(环氧树脂)中，制作了一组共6块非均质样品，其组分含量如表1所示.石英砂尺度(平均直径)分别为6 mm、2 mm、1 mm、0.25 mm、0.1 mm和0.05 mm.样品的制作过程如下：(1)按照表1确定环氧树脂、固化剂、石英砂的质量并分别进行称取；(2)将环氧树脂和固化剂混合，充分搅拌后作为低速基底介质；(3)将石英颗粒加入到前述基底介质中，再次进行充分搅拌后放入真空系统，抽去混合介质中气泡；(4)将混合介质倒入圆柱形模具，放入40°恒温烤箱中48h；(5)待环氧树脂完全固化后，从模具中取出样品，对样品两端进行磨平精细加工，即完成样品制作.设计好的体积含量能够避免出现环氧树脂和石英砂分层固化的现象.图4为制作好的样品图，从每个样品对应使用的石英砂颗粒可以明显看出其尺度变化.

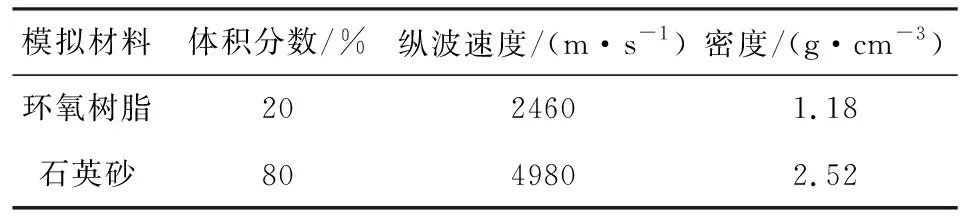
表1 不同尺度非均质样品组分含量Table 1 Component content of heterogeneous samples with different scales

2.1.2 速度测试

由于地震物理模拟所使用的超声频段为50 kHz至1000 kHz，即在1∶10000的比例因子下模拟地震频段5 Hz至100 Hz，因此采用主频为1000 kHz、500 kHz、250 kHz、50 kHz的纵波换能器对样品进行了纵波传播速度测试.为了消除其他因素，只考虑尺度非均质性对波传播速度的影响，首先在不同频率下对钢样、石英玻璃、有机玻璃、环氧树脂4个均质样品的纵波速度进行了测试，来确定物理模拟超声频率段内频率对波传播速度的影响程度.图5为四个均质样品的速度值随着频率的变化情况.可以看到，对同一块均质样品，在50 k～1000 kHz范围内纵波速度基本上是保持恒定不变的.对于有机玻璃及环氧树脂样品，纵波速度在1000 kHz时测试值略微大于50 kHz时测试值，这与速度传播理论也是相符的，但总体速度差异均在2%以内，基本可以认为地震物理模拟的50 k～1000 kHz 频带范围内均质样品纵波速度是恒定不变的.

随后，分别对不同尺度非均质样品进行了纵波速度的测试，图6是实测波形图.可以看出，在相同频率下，不同尺度样品的初至时间不同，说明波传播速度出现了变化.另外，频率越高，这种速度差异越明显.将6个不同尺度样品的速度值随着频率的变化情况在图7中给出.可以看出，对于不同尺度样品，其纵波速度都是随着频率的增加而增大.在相同频率下，大尺度样品的速度要高于小尺度样品；这种尺度带来的速度差异在高频时更加明显.可见在地震物理模拟中尺度非均质性会对纵波速度产生很大影响.

图4 不同颗粒尺度非均质样品Fig.4 Heterogeneous samples with different particle sizes

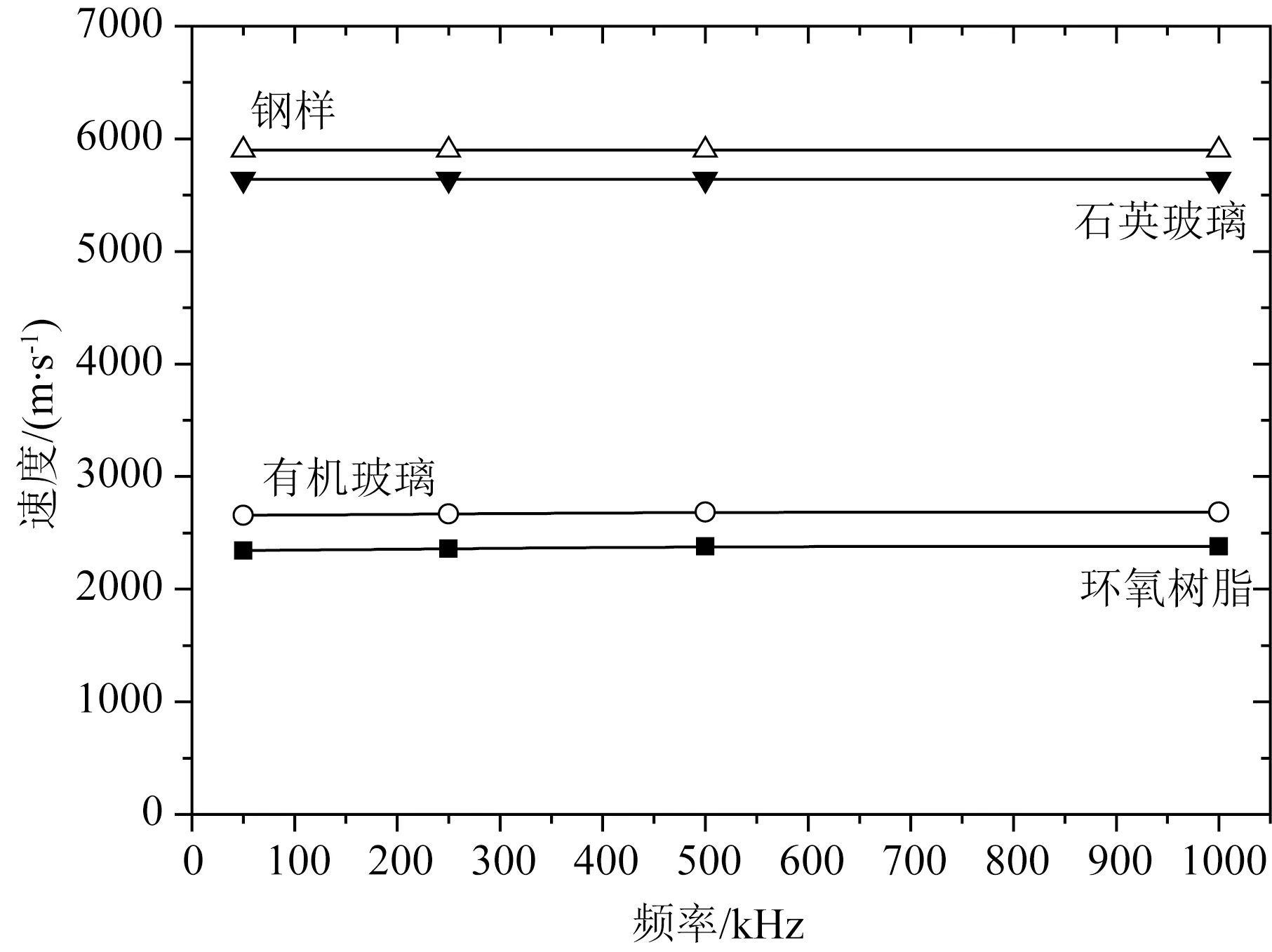
图5 物理模拟超声频段下均质样品速度随频率变化情况Fig.5 Change of velocity of homogeneous sample with frequency in physical simulation ultrasonic frequency band

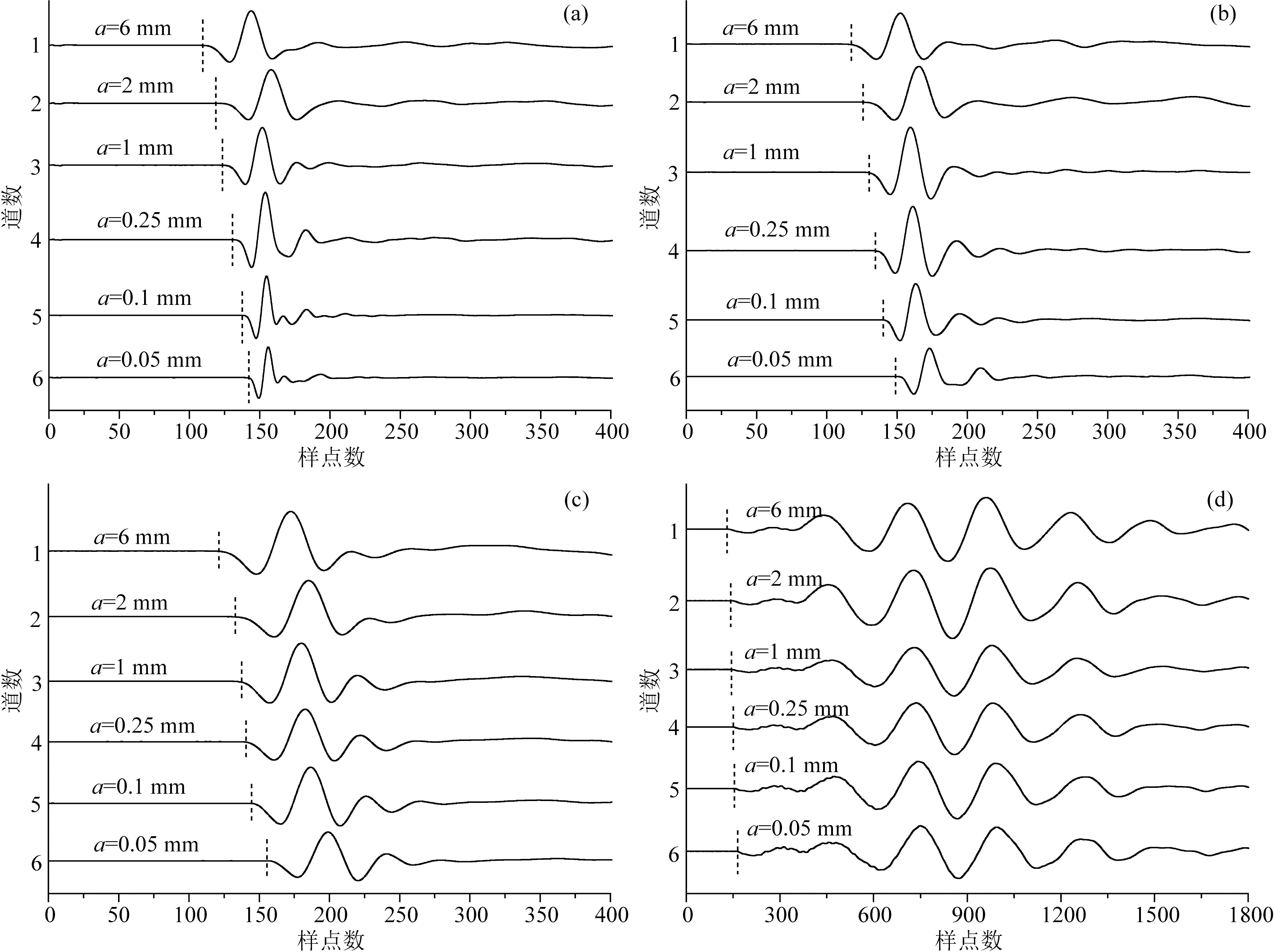
图6 不同主频下非均质样品速度测试结果(a) 1000 kHz; (b) 500 kHz; (c) 250 kHz; (d) 50 kHz.Fig.6 Test results of sample velocity with different scales under different main frequency

2.1.3 干扰波/有效波能量测试

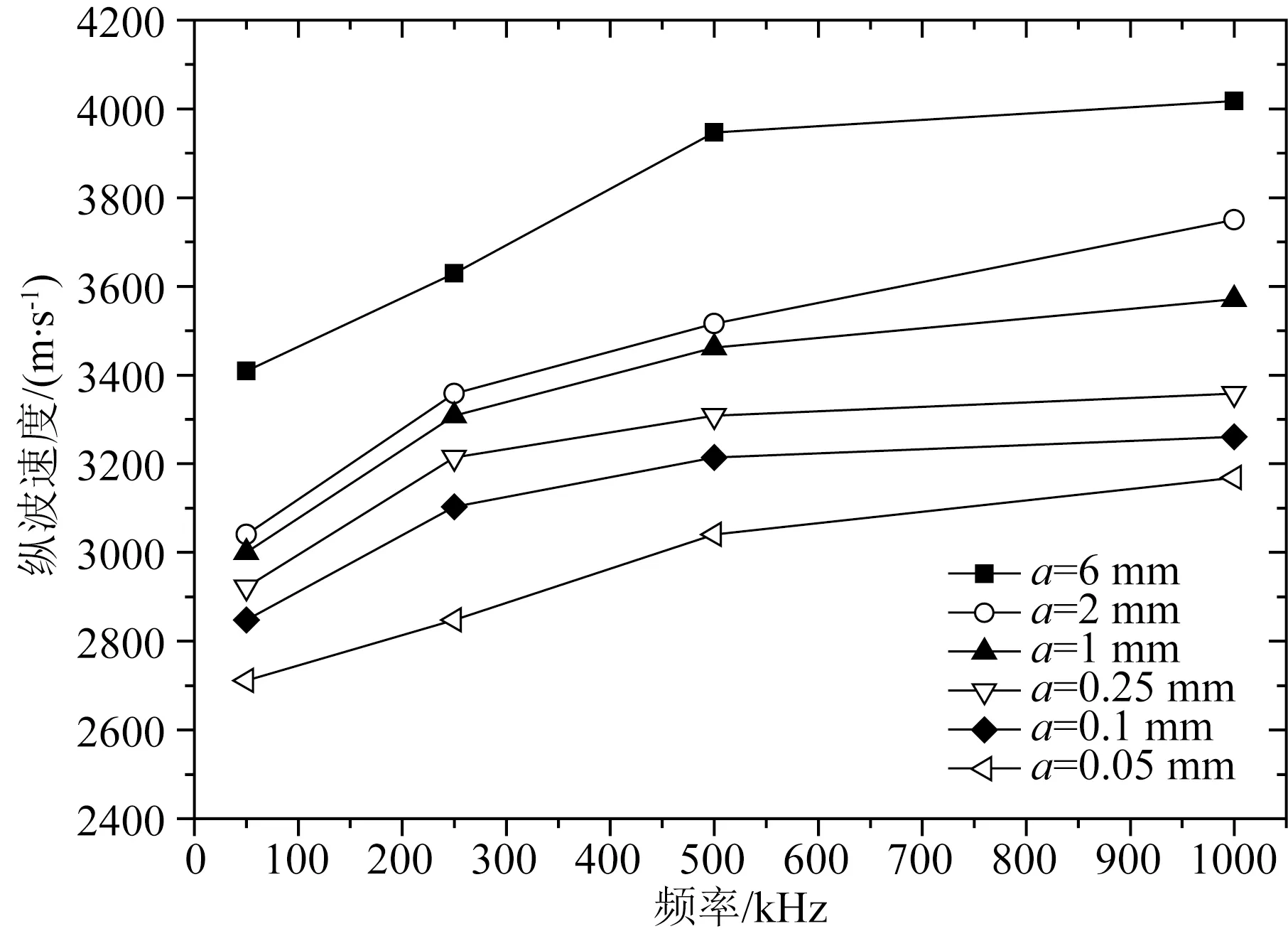
图7 不同频率下不同尺度样品速度变化Fig.7 The velocity change of different scale samples under different frequencies

尺度非均质性不仅会对波传播速度产生影响，同样会产生散射波等干扰波，从而对有效波的能量产生影响.在这里将尺度非均质性产生的各种散射波统称为干扰波，通过对不同尺度非均质样品采用相同传播长度的激光测振多点观测，定量研究颗粒尺度对有效波能量的影响.图8为实验观测示意图，每个样品固定在试验台上，在样品底端中心位置分别设置主频为1000 kHz、500 kHz、250 kHz、50 kHz的纵波换能器，激发出超声波在样品内传播.在另一端距离圆心等距的圆形测线上设置20个点激光测振观测点，来检测振动并接收波形.对于6块非均质样品，在进行激光测振时，震源中心点、样品底部和顶部中心点、20个激光测振观测点的圆心保持在一条直线上.即震源-测振仪之间保持零度发射超声信号，20个观测点同角度接收测振信号的位置关系.这样可认为在每个观测点处超声波具有相同传播长度，速度变化仅是由尺度非均质性引起.

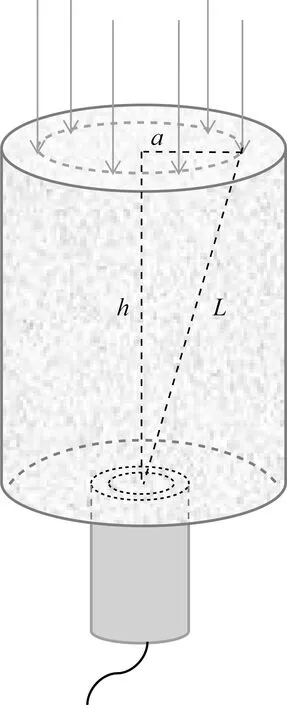
图8 非均质样品激光测振多点观测Fig.8 Multi point observation of laser vibration measurement for heterogeneous samples

当波在均匀介质中传播时，不同位置的观测波形显示出高相似性，其可以忽略不计的差异来自于实验误差.由于同一块样品的20个观测点具有相同的传播距离，可认为观测波形的差异是由非均匀性引起的.在第i个观测点，在时间t，每道信号是有效波和干扰波的叠加.有效波是20道观测波的平均值，见公式(1).干扰波是非均质介质内各点散射波的综合效应.有效波和干扰波分别描述了介质物理特性的平均和随机波动. 公式(1)为

(1)

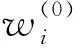
根据公式(1)，可以将干扰波从每一道观测信号中分离出来.将每个样品中20道观测波叠加得到的平均波形，认为是该样品在此频率观测下的有效波.每道信号减去有效波，可分离出20道信号分别对应的干扰波，再将20道干扰波进行叠加得到的平均波形，认为是该样品在此频率观测下的干扰波.图9中显示的是提取每个样品在250 kHz频率下的有效波及干扰波的波形对比，其中黑色实线为有效波的波形，灰色虚线为干扰波的波形.分别提取两道波形的最大振幅进行对比，可计算出此道的干扰波与有效波的能量比.对每块样品在4种频率测试下的波形均进行类似操作，即可得到全部的干扰波/有效波的能量比变化情况.

2.2 数据分析

2.2.1 速度与λ/a关系

前人的研究表明，介质非均质性对波传播的影响是与地震波在介质中传播波长λ及非均质体尺度a相关.对于6块非均质样品，用游标卡尺分别量取样品长度h、激光测振点到样品顶部中心点的长度a，利用公式(2)计算出超声波传播长度L.随后，从激光测振结果中提取出超声波在样品内的传播时间t，利用公式(3)即可计算得到传播速度v，并将所有速度值标定到图10中. 公式(2)和(3)为

(2)

(3)

从图10给出的纵波速度随λ/a(波长/非均质尺度)的变化关系中可以发现，λ/a的变化范围为0.67～579.82，观测到总的速度偏移为1107 m·s-1，约占最小测量速度的38%，速度变化非常显著.当λ/a<2时，速度波动很小，属于射线速度范围.当2<λ/a<100时，随着λ/a的增大，速度迅速减小，属于散射速度范围.当λ/a>100之后，速度趋向于一个常数，属于等效介质速度范围.因此认为地震物理模拟超声频段下，从射线速度向散射速度的转折点出现在λ/a≈2处，散射速度向等效介质速度的转折点出现在λ/a≈100处.从另外一个角度来看，当进行物理模拟时，当满足λ/a>100(λ为超声波在介质中传播波长，a为组成模拟介质的颗粒尺度)条件时，模拟储层在速度上可以看成是等效介质，在此基础上才能进一步模拟由储层结构、油、气所引起的储层速度参数变化.

2.2.2 干扰波能量比与λ/a关系

对不同主频下所有非均质样品的有效波与干扰波进行了提取，并计算了干扰波/有效波能量比，得到了干扰波/有效波能量比与λ/a关系图，如图11所示.从图中可以看出，对于颗粒介质，50 k～1000 kHz频段内散射波能量显著，但当λ/a>200后，干扰波与有效波能量比小于5%，可认为属于随机噪声.因此可以认为λ/a>200时在能量上满足等效介质条件.

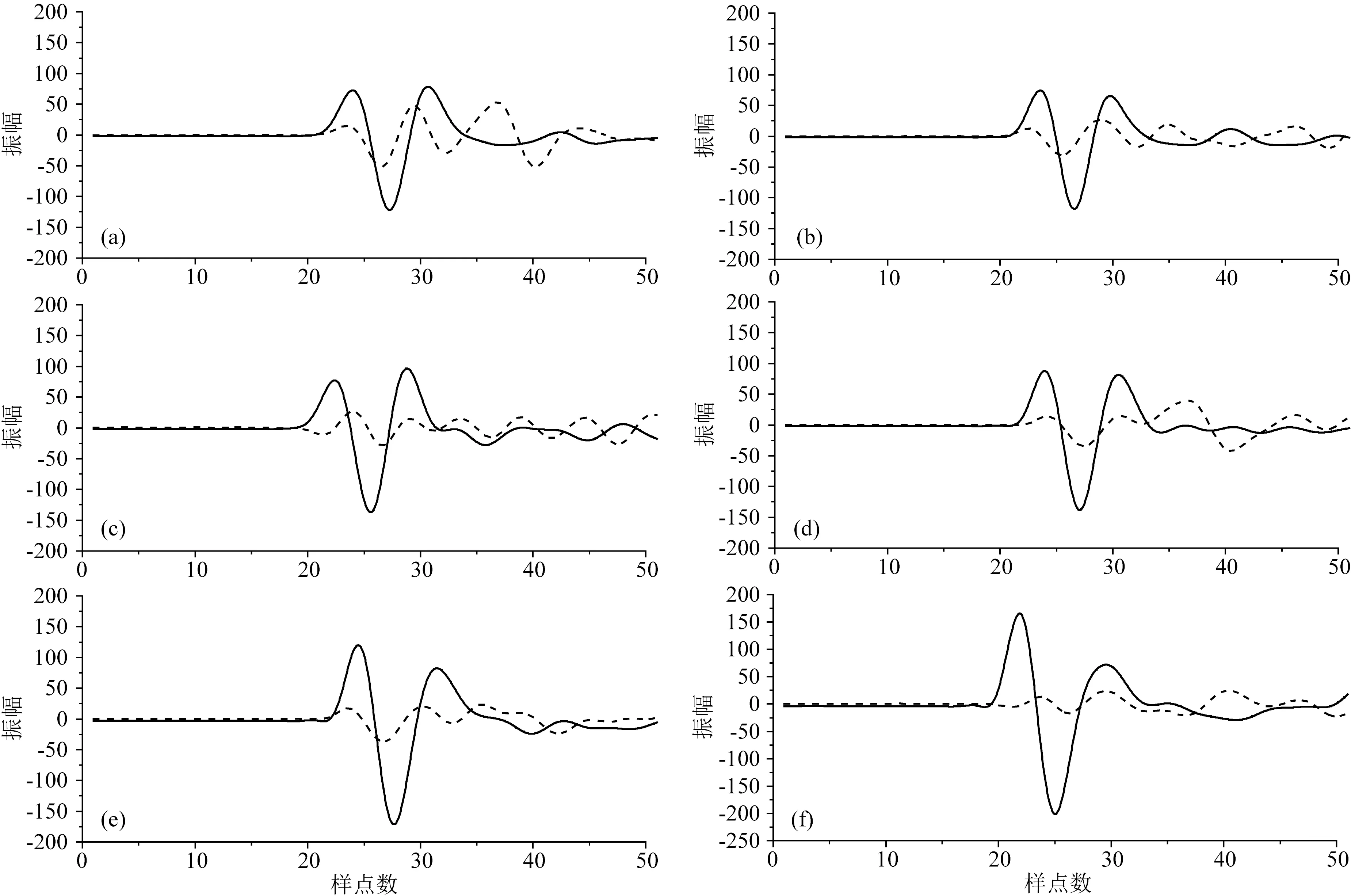
图9 250 kHz主频下非均质样品有效波与干扰波波形对比(a) a=6 mm; (b) a=2 mm; (c) a=1 mm; (d) a=0.25 mm; (e) a=0.10 mm; (f) a=0.01 mm.Fig.9 Comparison of effective wave and interference of heterogeneous sample wave under 250 kHz main frequency

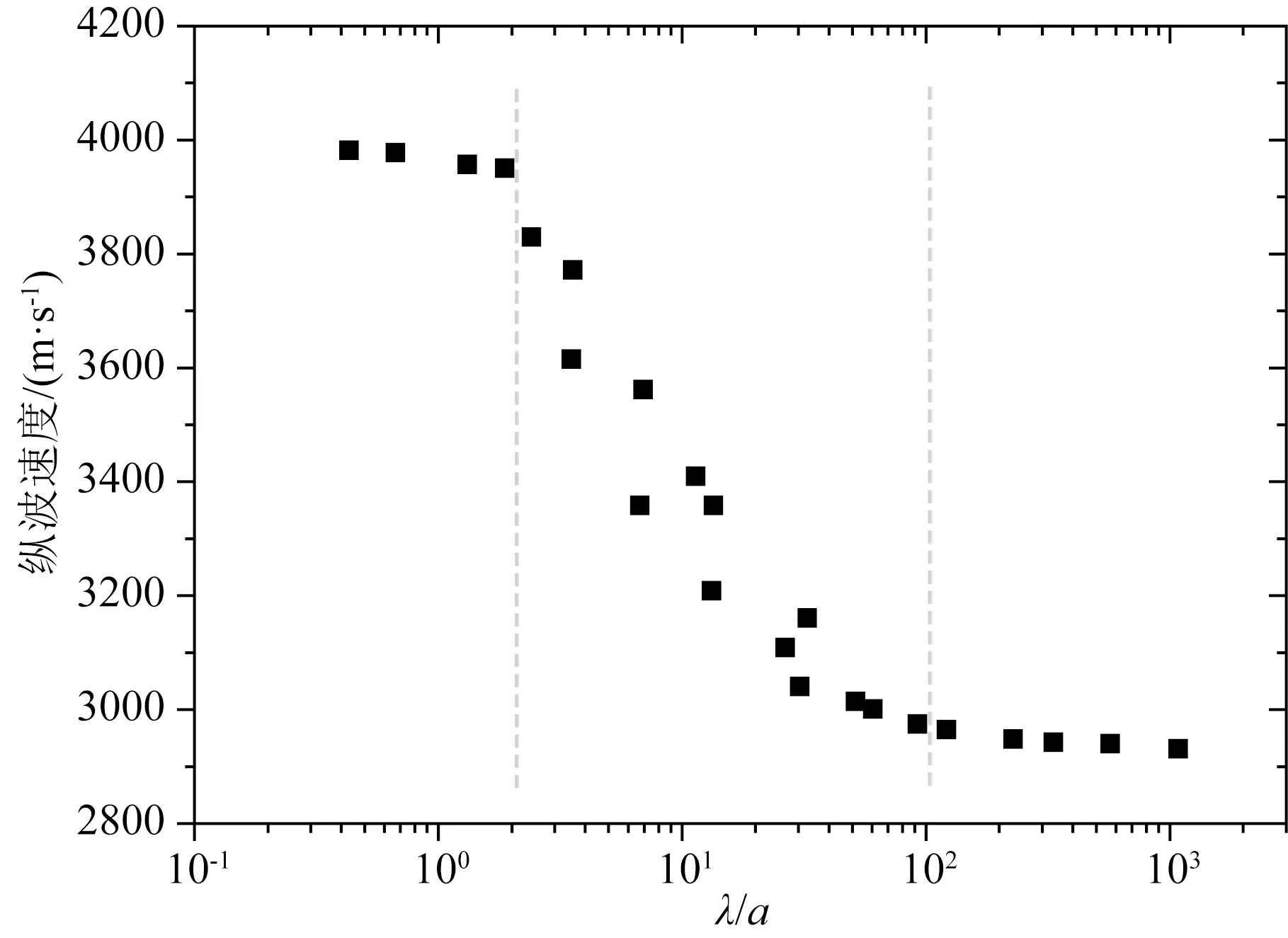
图10 物理模拟超声频段下速度变化与λ/a值关系对比Fig.10 Comparison of velocity change and λ/a value in physical simulation ultrasonic frequency band

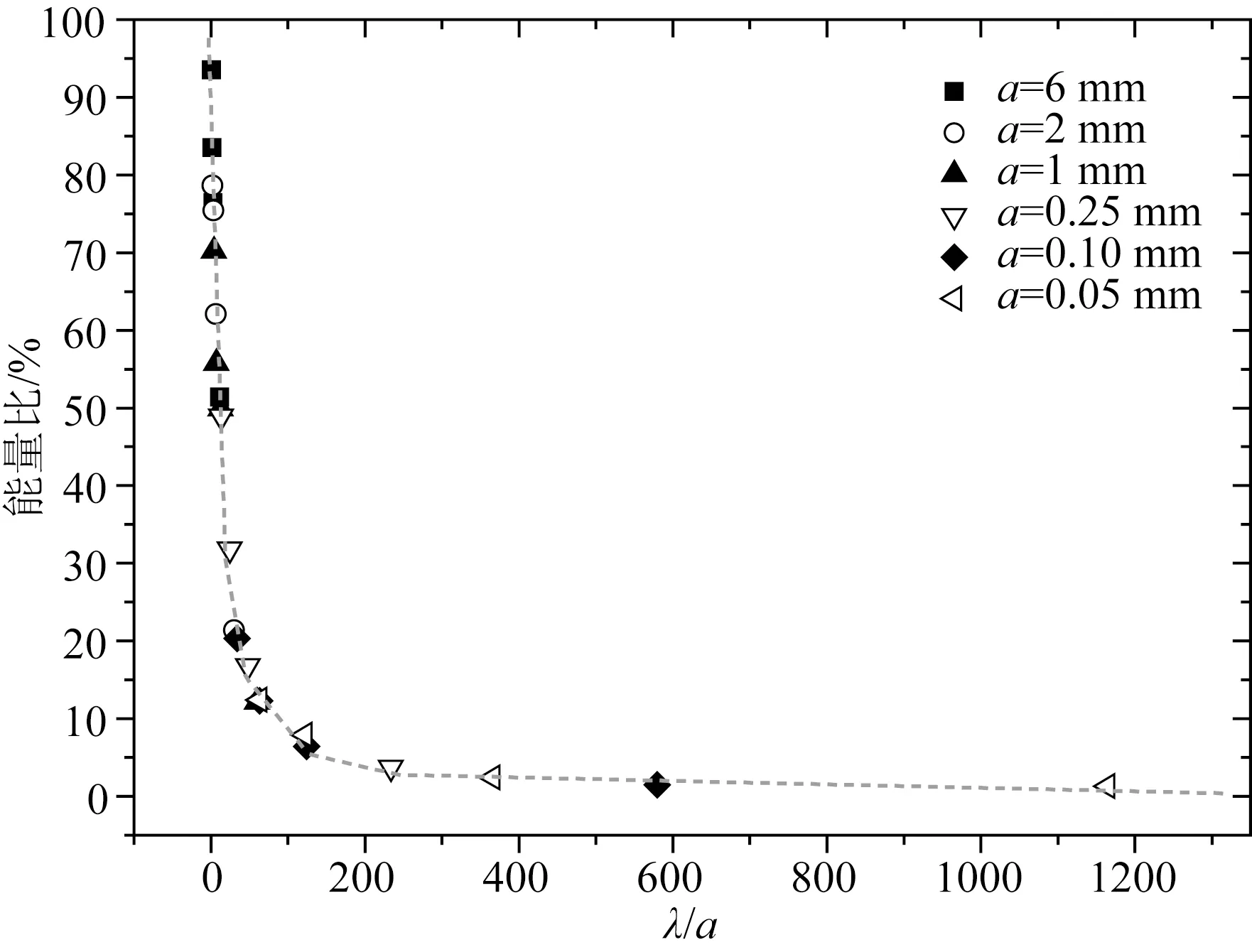
图11 物理模拟超声频段下干扰波/有效波能量比与λ/a关系图Fig.11 Energy ratio of interference wave/effective wave and λ/a of inhomogeneous sample in the physical simulation ultrasonic frequency band

在物理模型材料选择和构建时，应根据此特征判断选取是否合适，尤其是需要将颗粒介质模拟储层视为等效均匀介质，而仅考虑流体带来的模拟储层参数变化情况.

2.2.3 讨论

基于前述非均质样品的实验结果及分析，探索了介质尺度非均质性引起的纵波速度及干扰波/有效波能量比与λ/a关系.在实际介质地震勘探中，随着油气勘探目标的复杂性不断提高，传统地震勘探理论中的层状介质或者均匀介质假设已不能满足研究要求，想要得到更精确的地下信息，就必须建立基于非均匀介质假设的地震勘探理论.但由于实际介质的非均质性更为复杂，包括尺度、岩性、物性、含油气性以及地层特征等等因素，因此基于本论文实验结果得到的速度偏移与尺度非均质性关系并不具有普适性，不能直接推广至实际应用.想要更加深入的探究非均质地震勘探理论，还需要进一步开展大量的基础研究工作.

3 结论及认识

通过实验测试及分析，针对了换能器指向性及介质尺度非均质性对地震物理模拟实验数据的影响规律开展研究，得到了以下结论及认识：

(1)利用激光测振方法能够得到更加精确的换能器振幅指向性特征，计算得到补偿系数对模型数据进行补偿，能够提高模拟数据振幅及AVO特征的准确性.

(2)在物理模拟超声频段下，射线速度向散射速度的转折点出现在λ/a≈2处，散射速度向等效介质速度的转折点出现在λ/a≈100处.当满足λ/a>200条件时，干扰波与有效波能量比小于5%，可认为满足储层物理模拟的等效介质条件.

本文主要针对地震物理模拟方法自身因素对实验数据的影响开展分析并加以校正，逐步实现含流体储层地震物理模拟的技术可行性，提高模拟数据的可信性和准确性.在此基础上，如何实现由流体引起的模拟介质的速度、衰减等参数变化能够与实际储层具有高度的物理相似性，是今后储层物理模拟需要继续攻克的技术难题.

致谢本文部分实验工作是在中国石油大学(北京)地球物理学院地震物理模型实验室完成，两位匿名评审专家为本文提出了中肯的修改意见，在此一并表示感谢.