纳米级超声造影剂的理论研究进展

杨茂发，李 敬，张现仁

(北京化工大学化学工程学院，北京 100029)

在许多疾病的诊断中，超声显像已经被证明是一种很有前途的工具，具有高灵敏度、可及性、便携性和低成本等优点。超声造影剂是一类能够显著增强医学超声检测信号的诊断试剂，可使一些不能显影或显影不佳的器官或组织的成像效果得到改善[1]。超声信号的增强来自于超声造影剂中的气体与血液之间的高声阻抗差异[2]。较为成熟的超声造影剂多为微米级，其直径在1～10 μm，能够自由通过肺毛细血管，且微米级的气泡在医学超声频率下可以产生共振现象，使得气泡散射的超声信号大幅度增强。但是，微米级气泡因其循环时间短、尺寸大等缺点，不能穿过血管壁进入组织，从而限制了其对血管外疾病的显影能力，使其仅能应用于血池显像。对于炎症及栓塞部位处的血管，由于血管较狭窄，微米级超声造影剂有时也无法顺利通过。为了解决这些问题，众多研究人员设计了纳米级的超声造影剂，纳米级超声造影剂尺寸更小、穿透力更强，可以穿过病变组织的血管壁进入组织内，从而可以实现血管外各组织的成像。其中，基于纳米气泡和纳米液滴的纳米级超声造影剂被广泛研究，并被证明可以用来替代微米级超声造影剂[3-9]。本文介绍了2种典型的纳米级超声造影剂：基于纳米气泡的超声造影剂和基于纳米液滴的超声造影剂。首先，第一部分给出了气泡在超声作用下的基本理论及振荡运动模型；其次，第二部分介绍了基于纳米气泡超声造影剂的稳定性研究，以及对纳米气泡增强超声成像可能性原因的分析；然后，第三部分介绍了基于纳米液滴的超声造影剂，主要描述了液滴核心的选择，以及相变造影剂的气化机制；最后，第四部分讨论了纳米级超声造影剂目前存在的问题及应用前景。

1 超声造影剂成像的基本原理以及振荡运动模型

超声成像是利用超声波在不同的生物组织中具有不同的声阻抗来实现的。超声波在传播过程中遇到声阻抗不同的界面时，会发生声波的反射、透射、散射及衍射，使得入射声波的能量发生传播方向上的改变。之后，利用返回换能器不同强度的回声信号获得结构信息，重建组织分布图像。然而，当相邻的人体组织的声阻抗比较接近时，人们很难从显示的图像上区分不同的组织。此时，超声造影剂就显示出极大的优势。超声造影剂的内部气体具有较强的散射能力，能够产生高效的声波散射，可以增强待检查部位与周围组织之间的声阻抗，从而增强其背向散射信号的强度，使获得的超声图像更加清晰，便于诊断[10]。

超声波的波长λ由频率f决定：λ=c/f，其中c为声速。对于医学超声频率而言，波长多在200 μm～1 mm。超声造影剂多为微米级和纳米级，这就意味着超声造影剂的尺寸半径、直径远小于声波的波长。对于小尺寸造影剂的声波散射，最简单的模型为Rayleigh模型。Lord Rayleigh给出了一个小物体发出声波的模型，当用该模型表示散射截面时，其表达如式(1)[11]。

其中：σs——造影剂的散射截面，m2；

r——造影剂的尺寸半径，m；

k——声波的波数，k=2π/λ；

ρ与ρs——周围液体和造影剂的密度，kg/m3；

κ与κs——周围液体和造影剂的绝热压缩系数，m2/N。

根据Rayleigh模型，式(1)括号外的项给出了散射截面与造影剂尺寸和声波频率的关系。由模型公式可知，散射截面与频率的四次方或造影剂半径的六次方成正比。括号内的项与造影剂的材料参数有关，决定了不同的造影剂具有不同的散射特性。前一项描述了小尺寸造影剂对周围介质压缩性差异的影响，后一项描述了小尺寸造影剂对周围介质密度差异的影响。当两者的压缩性差异和密度差异越大时，其粒子的散射截面越大。De Jong等[12]为了确定哪个参数对散射截面的影响更大，在周围介质为水的情况下，考虑了压缩性和密度相差较大的2种材料的散射粒子：具有相同半径(1 μm)的刚体球和气体球，如表1所示。

表1 气泡与铁粒子在式(1)中各项的比较Tab.1 Bubbles and Iron Particles Comparison between the Terms in Equation (1)

由表1可知，气体球与刚体球(铁粒子)在散射截面上存在显著差异，1 μm气泡的散射截面是同等大小刚性球的1亿倍以上。尽管气体(空气)与刚体(铁)之间的密度相差较大，但密度项对散射截面的贡献相对较小，而压缩项对散射截面具有显著影响。Rayleigh模型给出了引起声波散射的机制和性质，并说明了气泡具有压缩性是强大的声波散射体的原因。但是，Rayleigh散射不是一个适合描述气泡声波散射的模型，因为它忽略了气泡的共振现象和声吸收。

更好的模型是把气泡看作振荡器[11]。当使用气泡作为超声造影剂时，气泡的机械共振，即气泡的刚度和惯性会对散射截面产生重要的影响。气泡在超声作用下发生运动，平衡半径被扰动，封闭气体的压缩或膨胀会产生弹簧力来抵抗体积的变化。惯性主要是由于气泡周围的液体与气泡一起振荡，流动液体的质量给系统带来了惯性，气体的质量也会增加惯性。但是，由于液体的密度约是气体密度的1 000倍，气体的惯性可以忽略不计。对于气泡的振荡运动方程，Omfrs[13]通过研究在无限不可压缩液体中产生空化的问题，率先对气泡的运动进行了分析。后来，Plesset[14]研究发现，外驱动压力和表面张力的影响是空化向气泡动力学转变的主要步骤，Plesset的研究同样忽略了液体的可压缩性影响。Plesset的研究假设气泡内的气体压力是均匀的，且服从多元定律，描述了蒸汽气泡的动力学。Noltingk等[15]对充气气泡做了同样的试验，研究了黏性对不可压缩液体中气泡运动方程的影响。这些研究者的贡献共同促成了Rayleigh-Plesset-Noltingk-Neppiras-Poritsky (RPNNP)方程[16]，简称为RP方程。该方程准确地描述了一个球形理想气泡在无限不可压缩流体中径向振荡的状态。Plesset等[17]对这个方程的发展进行了历史回顾，如式(2)。

(2)

其中：R——气泡瞬时半径，m；

p0——静水压强，Pa；

pi(t)——无限远处在液体中的入射超声波压力，Pa；

pg(t)——气泡内的均匀气体压力，Pa；

ρ——液体的密度，kg/m3；

σ——气液表面张力，N/m；

η——液体的黏度，Pa·s。

气体遵循一个具有多变指数的多变压缩定律，使得气泡内部压力如式(3)。

(3)

其中：R——气泡瞬时半径，m；

R0——初始气泡半径，m；

κ——气体多变指数；

σ——气液表面张力，N/m。

若气体的热扩散长度比气泡的半径大，气泡将表现为等温性质(即κ=1)；若气体中的热扩散长度远小于气泡半径，且气泡半径远小于气泡中的声波波长时，气泡将表现为绝热性质，此时，多变指数κ=γ，γ为气泡内气体的比热比[17]。

当把气泡看作是一个线性简谐振子，假设气泡在小振幅极限下振荡时，可以将RP方程进行线性化处理，线性化后可得到一个谐波-振子形式的方程[18]，如式(4)。

(4)

其中：x——气泡的径向偏移，m；

β——阻尼常数；

ρ——液体的密度，kg/m3；

ω0——气泡的固有频率，s-1。

虽然这个假设仅局限于小振幅振荡的情况，但它可作为一个简单而有力的工具，用来揭示环境对气泡响应的影响，可用于研究气泡动力学的许多方面，如气泡的固有频率、声散射特性和热阻尼效应[19-22]。将R(t)=R0[1+x(t)]带入RP方程中，可得到其固有频率，如式(5)。

(5)

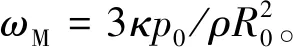
距离球形气泡中心r处的散射的超声压力如式(6)[24]。

(6)

其中：ps(r,t)——气泡散射声波压力，Pa；

ρ——液体的密度，kg/m3；

r——与气泡中心的距离，m；

Vb——气泡的体积，m3。

一般情况下，散射截面定义为散射声波功率与入射超声强度的比值，进一步化为用入射声波和散射声波的压力振幅表示，可得散射截面，如式(7)

(7)

其中：σs——散射截面，m2；

Ws——散射声波功率，W；

Ii——入射超声强度，W/m2。

假设入射超声压力表达式为pi(t)=pacosωt，且在气泡小振幅振荡的情况下，可求得气泡的散射截面，如式(8)。

(8)

其中：ω0——气泡固有频率，s-1；

ω——入射声波频率，s-1。

此散射截面表达式是在线性极限的情况下求解得到的，把气泡作为线性振荡器，考虑了气泡在超声作用下产生的共振现象。在共振频率附近和共振频率之上，气泡的散射与Rayleigh散射有强烈的偏离，充分体现了此模型与Rayleigh模型的差距，并说明了气泡在产生共振时，其散射截面可达到最大值。Hoff[11]在其书中对这两种模型进行了比较，证明了当驱动频率远低于共振频率时，Rayleigh模型的散射截面与振荡器模型的散射截面相等。Hilgenfeldt 等[24]统一了针对自由气泡不同情况的处理方法,研究表明，当气泡振动的振幅足够低，即被认为是线性的时候，相应的散射截面与从各向同性散射的分析得出的截面相同。

经大量试验证明，只有当马赫数(气泡壁的速度与液体中的声速之比)很小时，RP方程才能对气泡的运动模拟较好。然而，当入射压力幅值较大时，声马赫数接近于1，声辐射阻尼和液体可压缩性变得很重要[25]，此时假设液体不可压缩的RP方程便不再适用。针对较高的压力振幅和较大的气泡径向振荡的情况，大量研究者提出了对RP方程的扩展，其中包括Keller方程、Herring方程和Gilmore方程[26-29]。Prosperetti 等[30-31]均证明了存在一个单参数的方程，其可以用来描述无界液体中的气泡振荡，如式(9)。

(9)

其中：λ——一个引入参数；

c——液体中的声速，m/s。

pB(t) ——气泡壁处液体的压力，Pa。

此方程中的参数λ=0时，即可演化为Keller方程；参数λ=1时，即可演化为Herring方程。

然而，自由气泡往往是不稳定的，尤其是尺寸小到微米级甚至纳米级的气泡，其在体内的持续存在时间很短，故作为超声造影剂的气泡通常具有一定厚度的包膜，以增强气泡的稳定性。对于纳米气泡，往往还需在包膜内添加表面活性剂或者固体颗粒[32-36]。这种包膜一般被认为是一种具有黏弹性的物质。包膜的表面黏弹性可以显著增强气泡的共振频率和阻尼，同时包膜的涂层可以加剧气泡的非线性振荡效应。起初，Roy等[37]将气泡包膜看作一种简单的黏性液体，得到了一种含有包膜性质的广义RP方程，并证明了模型的预测与瞬态空化阈值的试验测量结果一致。De Jong等[38-39]将气泡包膜建模为黏弹性固体层，研究了气泡的声衰减、后向散射和非线性振荡。Church[40]考虑到包膜具有一定厚度，假设包膜为一层不可压缩的黏弹性固体，提出了一个修正的RP方程。Hoff等[41]随后开发了一个模型，利用包膜的黏弹性来描述聚合物封装微泡的行为。

此外，对于脂质包膜的特性，不能简单地将其纳入仅描述气泡振荡的径向分量的模型中，脂质分子在气液界面上发生自组装。当脂质包膜被压缩时，单分子脂质层会发生可逆的弯曲或脱落到溶液中[42]。Marmottant等[43]提出了第一个专门研究脂质封装气泡的非线性行为的模型。在原有的工作中加入有效表面张力的概念，通过定义不同气泡状态的表面张力使得模型高度非线性化，成功预测了脂质封装气泡振荡的非线性行为。之后的模型均是通过对气泡包膜进行严格的力学处理来捕捉这些非线性。Tsiglifis等[44]将气泡包膜建模为非线性弹性固体，应变-软化本构定律再现了共振频率随着气泡振幅的增大而减小的趋势。其他的非线性模型利用与半径相关的表面弹性来建模，在最近的模型中，考虑了弯曲弹性用来理解非球形气泡的振荡[45]。关于包膜气泡的振荡模型或者黏弹性介质中的气泡模型，还有很多很好的综述[46-48]，可以从这些综述中了解不同模型的详细信息。

然而，上述对于气泡运动方程的推导均是在微米级气泡或者更大尺度上进行的。近年来，随着纳米级超声造影剂的发展，人们尝试着对纳米级气泡在超声下的运动过程进行模拟。Jafari等[49]利用Marmattont[43]提出的气泡运动模型，模拟了半径为200 nm的气泡在超声下的振荡运动行为。研究发现，纳米气泡外的脂质包膜对气液界面处的表面张力具有较大的影响，从而使气泡在超声下振荡运动的共振频率发生变化，使得气泡在较低的超声频率下仍具有较强的响应。这与线性理论预测相矛盾。Pellow等[50]采用Marmottant 模型[43]与Yang等[51]改进的Keller-Miksis 方程，分别模拟了在液体和弹性连续介质中的纳米气泡行为。通过模拟，发现脂质包膜在最初接近弯曲状态或破裂状态时，气泡的行为可以在试验中捕捉到。尽管纳米气泡的行为已被模拟研究，但也仅是基于已成熟的运动模型，因此在之后的研究中，对于直接在纳米气泡尺度上的运动方程的探索是非常必要的。

2 基于纳米气泡的超声造影剂

纳米气泡超声造影剂与常规超声造影剂一样，内核一般为全氟化碳(PFCs)或六氟化硫气体，也有部分使用氮气或甲烷等气体，其散射原理一致。气体具有较大的声阻抗，增强了不同组织或病变组织与正常组织的分辨率。只是纳米气泡超声造影剂的尺寸更小，达到了纳米级。使用纳米气泡作为超声造影剂，首先要解决的就是气泡在体内的稳定性问题。Epstein等[52]从理论上预测，直径<1 μm的未封装的气泡会在0.02 s内消散，人们根本无法检测到或对其进行表征。通常只有当气泡内的气体与溶液中溶解的气体达到平衡时，气泡才能保持恒定的大小。然而，由于拉普拉斯压力的存在，这个条件往往不能实现，气泡几乎不可能保持恒定大小。拉普拉斯压力是气泡(或液滴)内外的压力差，如式(10)[53]。

(10)

其中：σ——气泡界面的表面张力，N/m；

Pi——气泡内压力，Pa；

Po——气泡外压力，Pa；

R——气泡半径，m。

由式(10)可知，拉普拉斯压力与气泡的尺寸半径成反比。当内部气体离开核心时，在气泡内外压力差的驱动下，气泡会产生收缩，拉普拉斯压力增大，从而加速了内部气体的耗散，导致气泡进一步收缩，直至气泡破裂。拉普拉斯压力的存在，导致气体扩散，气泡溶解，因此，气泡在体内的溶解速度主要取决于界面的拉普拉斯压力。故可以从以下几个方面考虑得到稳定纳米气泡：在气泡界面加入表面活性剂、限制内部气体的扩散、控制气泡表面的结构，以及降低拉普拉斯压力等。很多报道均提到了气泡表面物质对气泡稳定性的关键作用。纳米气泡的外壳通常由脂质或聚合物组成，通过将表面活性剂或固体颗粒加入到这种外壳中，可以显著增强其抵抗气体损失、气泡溶解和气泡聚结的能力。

Dressaire等[54]研究了一种表面活性剂封装的微气泡，该表面活性剂可在气泡表面自组装形成一个纳米尺度的六边形结构，并证实了平均半径<1 μm的该气泡的低气体扩散行为，且能持续稳定一年以上。 Krupka等[55]提出了一种简单的方法，将表面活性剂嵌段共聚物加入到脂质壳中，来制备稳定的纳米尺寸的气泡。结果表明，嵌段共聚物在控制脂泡尺寸方面是有效的，且嵌段共聚物的分子量、亲脂平衡(HLB)、嵌段共聚物与脂质的比例是决定脂泡尺寸的关键因素。但是，气泡的稳定性和回声性似乎不会因为气泡尺寸的减小而受到影响。Wang等[56]研究了在水中封装的空气纳米气泡的稳定性，使用了和传统的封装材料不同的表面张力为6.7 mN/m的氟化聚合物来封装气泡。理论证明，在超声作用下，此纳米气泡存活的时间是目前临床使用的商用微气泡的100倍。Hernandez等[57]研究了纳米气泡单层膜的界面特性，详细评价了嵌段共聚物加入纳米单层膜后的表面张力效应，证明了表面活性剂的加入有助于降低表面张力，从而降低拉普拉斯压力来稳定气泡，并表明这种效应只在某些成分中可见，随单层结构变化(晶体相或液晶填充)而变化。最近，Chu等[58]报道了一种用超顺磁性纳米颗粒修饰的聚合物封装纳米气泡，利用AFM峰值力轻敲模式研究了单个气泡在不同力下的受力曲线，得到了其刚度和杨氏模量，表明利用纳米粒子修饰的气泡可以增强其力学性能，使气泡更加稳定。

虽然封装包膜的存在可以降低气泡界面的表面张力，并抑制气体扩散，从而延长纳米气泡在体内的循环时间。但是，由线性理论预测可知，将气泡尺寸从微米范围减小到纳米范围时，对气泡在超声作用下的行为会产生显著的影响。气泡尺寸的缩小将会导致气泡的刚度增加以及共振频率的增加。这种情况在封装的气泡中更为明显。由上述线性气泡理论预测可知，这种封装的气泡将大大降低散射功率，并使共振频率远远超过在医学超声中使用的频率。在研究的最初阶段，这种观点导致了对回声纳米气泡的怀疑。然而，Oeffinger等[59]首次开发出了一种含有全氟丙烷的纳米级超声造影剂，并对其进行了声学测量。随后，陆陆续续有许多研究均报道了关于纳米气泡被成功用于血管内和血管外的成像[60-65]，且纳米气泡被认为在血管内和血管外的应用中具有优势，因为其有可能被动地穿透血管，进入组织内，从而可以应用到血管外。

纳米气泡能够高分辨率成像的一种解释可能得益于其在血流中具有较高的气泡数密度。假设试剂内气体的体积分数一定，平均气泡尺寸越小，其单位体积内的气泡数量越多，进而导致血流中具有更高的气泡数密度，这样便可抵消单个纳米气泡相对于微米气泡的散射差异[66]。

另一种解释是在气泡中引入的聚合物或者脂质包膜可以促进纳米气泡在压力阈值以上产生非线性信号，在包膜中加入的表面活性剂或固体纳米颗粒也有着非常重要的作用。Krupka等[55]以嵌段共聚物作为尺寸控制剂，形成了稳定的纳米全氟化碳脂质壳气泡。研究结果表明，嵌段共聚物能够增加脂质包膜的流动性，补偿了因气泡尺寸减小而引起的声信号损失，从而提高了气泡的回声强度。Jafari等[49]利用Marmattont模型[43]研究了表面活性剂稳定的脂质包膜纳米气泡，通过定义不同的初始表面张力，对初始半径为200 nm的气泡的共振频率以及径向位移进行了模拟。结果表明，当纳米气泡的初始表面张力低于0.01 N/m时，随着声压的增加，纳米气泡的共振频率会迅速减小，提出了脂质包膜的弯曲程度是纳米气泡在较低频率下仍具有较强活性的原因。紧接着，Pellow等[50]研究了由卟啉封装的纳米气泡，同样是利用Marmattont模型[43]来研究气泡的非线性响应，并在模型中引入非线性壳黏度的修正，分别模拟了微米气泡和纳米气泡散射功率随入射声压的关系。结果表明，微米气泡的散射功率随压力的变化逐渐单调增加，而纳米气泡则表现为一开始的急剧增加，随后便趋于稳定。但是，不同的初始表面张力具有不同的稳定值，且开始增加的速率也有所不同，再一次证明了纳米气泡的声学响应受到脂质包膜弯曲行为的影响。

对于在气泡包膜中引入纳米颗粒的造影剂，尤其是超顺磁性氧化铁纳米颗粒，其是一种双重造影剂，不仅具有良好的超声成像行为，还具有较强的核磁共振成像信号。超顺磁性氧化铁纳米颗粒因其顺磁性和生物相容性而受到研究人员的青睐。较多研究均表明，其颗粒的顺磁特性和药物包封能力使其在医药给药领域具有广阔的应用前景[67-69]。

众多研究均表明，纳米级超声造影剂可在体内超声成像，但上述理论研究表明气泡尺寸的减小必然会引起声音散射功率的降低，从而使得接收到的声信号相对于较大气泡有所损失，故如何选择纳米级气泡的尺寸相当重要。研究表明，疾病状态下(如肿瘤)的血管内皮间隙增宽，可容纳直径<780 nm 的物质通过。另外，纳米级气泡穿透力极强，可以在某些器官血管区外渗，通过增强的通透性和滞留效应(EPR)被动富集，呈现器官累积现象，引起特殊器官如肝、脾的显影[70]。故纳米级超声造影剂尺寸往往设计在 700 nm以内，使得造影剂可以自由通过肿瘤血管内皮间隙，有效地实现血管外显影，从而更广泛地应用于肿瘤及其他疾病的诊断与治疗。

3 基于纳米液滴的超声造影剂：相变造影剂

在纳米液滴超声造影剂中，最具代表性的就是相变造影剂。相变造影剂液滴体积更小、稳定性更好，同时其又具备微米气泡的声学特性等特点而得到广泛的应用。超声波可以使充满全氟化碳的纳米液滴发生相变，膨胀形成比原来液滴尺寸大5～6倍的微米气泡，这种现象称为声液滴汽化(ADV)。声液滴汽化后的现象有：在有限的粒子空间内，液态转变为气态，使液滴直径最大增加5～6倍；在界面涂层不均匀的情况下，液滴与气泡聚结或气泡之间相互合并；溶解的气体从小气泡扩散到大气泡。声液滴气化在诊断和治疗方面均显示出巨大的潜力[71]。

相变造影剂的液滴核心一般为全氟碳化合物，其不同的构型和链长可产生独特的分子量、密度和沸点的差异。在以往的研究中，多使用的是全氟戊烷液滴，其沸点为29 ℃，在室温下就可以产生液滴，且由于拉普拉斯压力的存在，在生理温度下过热的全氟戊烷液滴仍可保持液滴形式。Reznik等[72]使用声学和光学技术评估了全氟戊烷液滴的蒸发和体外产生的微泡的特性，包括大小、气化阈值、回声强度和非线性。Li等[73]研究了全氟戊烷纳米液滴的相变行为，并对相变机理进行了深入的探讨。基于全氟戊烷的纳米液滴已经被研究用于肿瘤组织中阿霉素的靶向和增强释放[74-75]。最近的研究则多使用沸点较低的全氟碳化合物，例如全氟丁烷，其在室温下通常是气体，可以通过某种方法转化为纳米级的液滴，在室温和体温下均很稳定。这种液滴在生理条件下可以稳定地抵抗其自发汽化，且此液滴的汽化压力阈值明显低于其他全氟碳化合物液滴的相变压力[76-78]。另外，还有一种方法可以用来降低液滴汽化所需的能量，即用具有不同沸点的全氟碳化合物混合形成液滴。Kawabata等[79]首次提出了这种方法，将全氟戊烷和十氟戊烷混合的液滴与只含一种氟碳化合物的液滴相比，验证了其液滴汽化所需的能量不同，其后也有许多相关的研究报道[80-82]。

尽管相变造影剂已被广泛研究，但声液滴汽化的确切机制尚未被完全解释。由Antoine蒸汽压方程可知，纯化合物的相变与温度和蒸汽压相关，故有一种假设认为相变是由液滴的声加热引起的。Antoine蒸汽压方程如式(11)。

(11)

其中：A、B、C——参数；

P——压力，Pa；

T——温度，K。

基于这个方程，Rapoport[83]计算了直径为500 nm的全氟戊烷液滴的汽化温度。结果表明，当液滴与水界面的表面张力为0.03 N/m时，全氟戊烷液滴的汽化温度大约为68 ℃，因此，热诱导液滴相变机制会受到纳米液滴较高拉普拉斯压力的阻碍。另外，由Antoine蒸汽压方程可知，随着液滴核心压力的增加，液滴发生相变所需的温度越高。由于拉普拉斯压力与半径成反比，这种效应在纳米液滴中变得更加明显。然而不管怎样，如果声加热是发生相变唯一确切的机理，那么增加超声脉冲持续时间，便可提高声加热程度，从而触发液滴相变，但事实并非如此。研究表明，在医用超声频率下，在1 ms以内增加超声脉冲的持续时间，并不会明显降低声液滴气化所需的气化压力[84]。Rapoport等[85]对具有较高沸点的液滴核心的声液滴汽化进行研究，结果表明，纳米液滴的汽化不仅发生在连续波超声下，也发生在工作周期为20%的脉冲超声下。相对于热诱导汽化，这种变化对液滴的加热可以忽略不计。说明，纳米液滴的相变并非是热诱导机制。同时，这项研究也支持了另一种令人信服的相变机制：由声空化等超声的机械作用引起。很多学者通过同时研究声液滴汽化和声空化的阈值，探究声液滴汽化和声空化的关系，结果表明，声液滴汽化可以由声空化作用而产生[86-87]。

声空化过程即当超声作用于流体时，流体中产生声压场，从而发生气泡或空腔的产生、增长以及崩溃的过程[88]。研究发现，由于空化核的存在，液体的抗拉强度远低于理论上的抗拉强度，故在医学超声的作用下，极有可能会发生空化现象。声空化的生物效应来源于产生的高温、高压和速度(即冲击波和液体射流的形成)，包括细胞侵蚀或裂解、分子降解和自由基的形成[89]。而声液滴汽化极有可能是由这种声空化带来的生物效应所引起[86]。

尽管液滴相变的主要机制还没有完全被解释，但是大量的研究均表明，影响声液滴汽化的压力阈值的因素包括：环境因素，如环境温度、压力及周围介质黏度等；液滴性质，如液滴直径、表面张力、沸点等；超声参数，如超声频率、脉冲长度等。Öquist[90]研究了不同超声参数对声液滴汽化效率的影响。结果表明：对封装的全氟戊烷液滴使用不同的频率设置时，声液滴汽化效率没有显著差异，而使用较长的脉冲持续时间对汽化效率有好处。Rojas等[91]评估了边界约束、静水压力和黏度对声液滴汽化压力阈值的影响。结果表明，周围组织和毛细血管壁的约束以及体内黏度的增加将会导致声液滴汽化压力阈值的增加，而增加静水压力对汽化阈值没有显著影响。Aliabouzar等[92]研究了液滴沸点和大小对声液滴汽化压力阈值的影响。结果表明，对于低沸点液体，无论液滴的平均粒径多大，汽化压力阈值均随着频率的增加而增加，而对于高沸点液体，较大粒径的液滴，汽化压力阈值随频率的增加而降低。

4 结语：存在的问题与展望

纳米级超声造影剂已被大量研究，并被发现其在血管外诊断成像中具有显著优势。同时，由于纳米系统具有一定的靶向能力，将纳米级造影系统与临床治疗相结合在肿瘤治疗方面可表现出其特定的靶向治疗优势。但是，在理论方面，纳米级造影剂仍存在的诸多问题未得到解决。首先，以纳米气泡造影剂为例，其可以穿过血管壁进入组织内，将它们置于了一个不同于血管内的物理环境中。虽然已经有许多关于边界附近微泡响应和限制血管几何形状的研究，但纳米气泡的动力学不能简单地从微米尺度的气泡动力学中推断出来。血管外的纳米气泡动力学行为，与气泡的尺寸、封装包膜的性质以及环境参数有关。血管外的纳米气泡动力学行为是复杂的，目前的研究对其还没有很好的阐述，基于纳米气泡超声造影剂的理论动力学模型仍有待于开发。其次，针对纳米液滴的研究，特别是在理论上的研究，仍然十分有限。尽管许多研究在试验结果中对纳米液滴相变过程进行了解释，但理论上纳米液滴相变的机理仍然尚未得到很好的阐述，需进一步从理论上了解如何在降低超声压力振幅时，同时提高声液滴汽化的效率。这些问题的深入研究对于新型纳米级超声造影剂的制备和临床应用具有重要意义。

对纳米气泡的动力学研究，在描述气泡振荡模型RP方程的基础上，应继续发展在黏弹性介质中和具有黏弹性界面的气泡的振荡模型，但需充分考虑气泡尺寸的减小以及通过表面活性剂稳定的气泡对其振荡产生的影响。在纳米液滴的理论研究上，应在对人体组织不产生破坏的低频率下，以降低声液滴汽化压力阈值为目的，采用MATLAB软件对不同超声参数、颗粒性质以及环境因素对液滴相变过程的影响进行研究，进一步了解声液滴汽化的主要机理。