测井曲线生成问题的机器学习建模范式*——以长宁威远地区页岩井为例

杨 静 陈云天 蒋春碧

(1. 唐山职业技术学院 河北唐山 063300； 2. 鹏城实验室 广东深圳 518000； 3. 北京大学 北京 100871)

测井曲线对于油气资源勘探开发研究至关重要，但在一些超深井中获得测井曲线往往非常困难，而且有些测井曲线的测量存在较大风险，比如涉及放射源的密度测井，导致部分测井系列被迫放弃测量。因此，在实际生产与开发过程中，希望能够基于部分已知的测井曲线，直接生成未测量的测井曲线。越来越多的研究者尝试通过机器学习来解决地质学和石油工程中的问题[1-5]。研究表明长短期记忆神经网络(long short-term memory，LSTM)在测井曲线生成问题上具有出色的表现，生成效果优于常规方法或全连接神经网络[6-7],擅长处理序列数据[8-9]，因此适合处理具有空间连续性的测井曲线问题。但是在实际工程应用场景中，测井曲线往往是多源复杂的，简单直接应用机器学习模型的效果并不理想。

本文针对多源复杂测井曲线生成困难的问题，基于机器学习方法提出了一套高效建模范式,该范式将建模过程拆分为数据完整性分析、交叉检验和收敛性分析等3部分，有助于提升数据质量、自动化评估模型性能和预估模型针对具体场景的适用性；并以长宁威远地区7口页岩气井的真实测井数据为例，成功生成了无铀伽马、钾能谱、钍能谱、铀能谱、横波时差和光电吸收截面指数，生成结果与真实值的变化趋势基本一致，验证了基于机器学习算法的多源复杂测井曲线生成方法的有效性，可以作为实际开发的参考。

1 研究区测井曲线情况

本文研究的页岩气井位于四川盆地的长宁和威远2个地区，数据来源及分布存在差异，且不同井中缺少的测井曲线种类也不一致，是多源复杂测井曲线生成问题的典型案例。研究共涉及5口训练井(M1至M5)和2口测试井(T1和T2)，实际资料共涉及13种测井曲线，如表1所示，分别为自然伽马(GR)、无铀伽马(CGR)、铀能谱曲线(HURA)、钍能谱曲线(TH)、钾能谱曲线(K)、补偿密度(DEN)、纵波时差(DT)、横波时差(DTSM)、补偿中子(CNL)、光电吸收截面指数(PE)、浅电阻率(RXO)、深电阻率(RT)和井径(CAL)。表1中Y表示对应井中包含此种测井曲线，N表示未测量的待生成测井曲线。特别说明，在后文验证模型效果的实验中，需要将预测值与训练过程未出现过的真实值进行对比，因此实验井中部分待生成测井曲线作为对比数据而隐去，记为H。

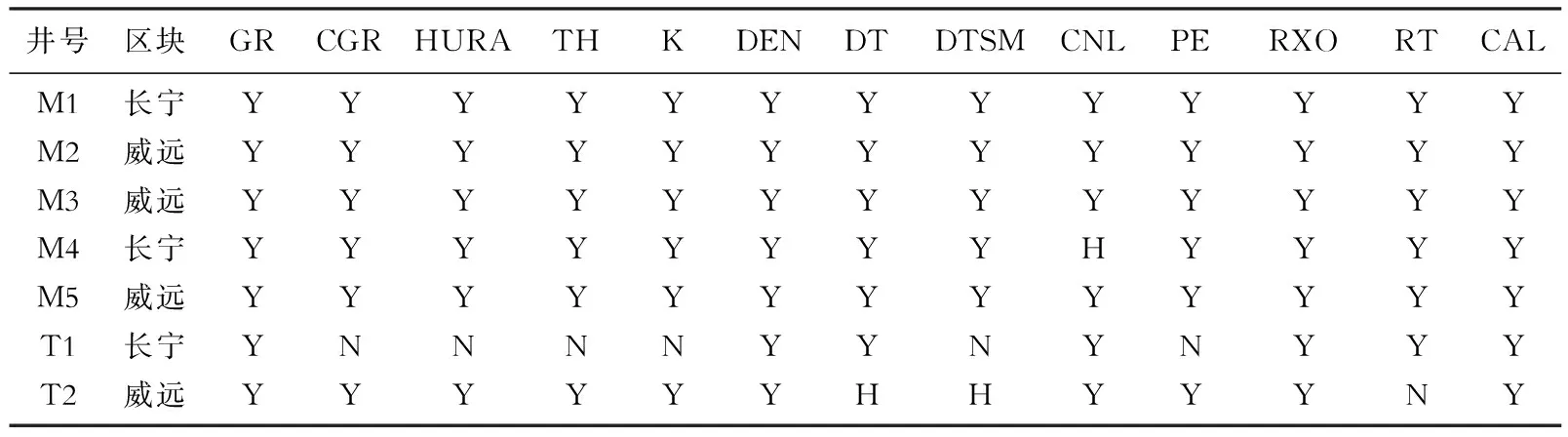
表1 研究区测井曲线数据情况Table 1 Well log condition in the study area

2 机器学习建模关键因素分析

机器学习算法，尤其是神经网络，拥有大量待确定的参数(如权重和偏置),这些参数使得神经网络具有极强的拟合能力，可以描述不同测井曲线之间复杂的非线性映射关系。在机器学习模型构建过程中主要有3个关键因素影响模型效果，即高质量训练数据、强拟合能力的机器学习模型以及数据同分布。建模过程只要满足上述3个条件，就可以确保生成结果可靠且具有高精度。

在实际应用中，需要重点关注上述3个制约因素。首先，在训练数据方面，训练数据量往往是给定的，获取新的数据费时且成本高昂。虽然目前已有针对小样本学习的研究[10-12]，但是数据量不足依然是制约机器学习应用的重要限制，因此实际建模过程往往关注于质量方面进行的改进。其次，在模型的拟合能力方面，实际应用中需要根据问题的难度选择神经网络的复杂度。原理上讲，神经网络有能力拟合任意函数关系，但是神经网络拟合能力越强则模型复杂度越高，数据需求也越大。因此实际建模过程要根据问题构建在有限数据下依然具有强拟合能力的机器学习模型。最后，数据分布(特征分布及特征间映射关系)对神经网络至关重要。神经网络的本质是根据训练数据学习不同变量之间的映射关系，其效果取决于训练数据集的大小以及训练数据集和测试数据集间的相似度。训练数据越多，训练集与测试集越为近似，则预测的效果越好。

因此，本文提出的基于机器学习算法多源复杂测井曲线生成方法主要关注于以下几点。①数据质量因素：将实际生产过程中收集的多源复杂数据进行有效清理，转化为神经网络易于利用的数据；②模型拟合能力因素：评估采用的算法是否有能力生成选定的测井曲线；③数据同分布因素：在实际生产中待生成测井曲线的真实值未知的前提下，预估该模型对于特定待生成井是否适用及结果是否可信。

3 建模方法

3.1 测井曲线生成模型建模范式

为了提升测井曲线生成模型的精度和可靠性，构造了图1所示的建模范式。首先数据处理环节可以有效提升数据质量，而后通过交叉检验进行模型选择，确保模型具有足够拟合能力，以及通过收敛性分析预估数据分布情况与模型适用性，最终对结果进行集成。

图1 多源复杂测井曲线生成模型建模范式Fig .1 Modeling paradigm of multi-source complex well log generation model

3.2 数据处理

神经网络对训练数据的数量和质量要求较高，因此需要采用必要的数据处理方法以提升数据质量。建模范式中主要包含异常值检测与清理、数据完整性分析及补全2个步骤。

针对异常值，首先通过设置固定阈值去除用于填充空值的异常值(如-999.25)并删除重复数据(往往位于测井曲线的首尾)。然后再通过动态异常值检测的方法剔除测井曲线内部异常点(式(1))，该方法是仿照k近邻(k nearest neighbor，KNN)算法构建的[13-14]，利用了地层连续性导致的测井响应连续性。该方法提取目标点及其周围k个数据进行差值计算，并与预设阈值对比，能够较好地识别出测井曲线内部离散的异常值。

(1)

式(1)中：Ri对应为目标点偏离程度；yi为目标点的数值，i为目标点的编号；yi,j为第i个目标点周围第j个临近点的数值；k为临近点总数，为超参数。

第2步是数据完整性分析与补全，主要是评估数据中是否存在较多的残缺值并基于模型进行补全。例如，训练井M4缺少补偿中子曲线(人为隐去，用来模拟实际建模数据存在残缺的情况)，可以选择直接删除M4井，只利用剩余的4口井进行建模，但是会使得原本不足的训练数据更加稀少。也可以尝试先构建一个通过4口井预测M4井补偿中子曲线的模型，由于该模型待预测变量较少，所以易于获得较好的结果。在M4井补全后即可使用全部5口井建模，有效提升训练数据量。需要说明的是，模型生成的补偿中子曲线并非实测值，不包含新的信息。但是由于生成了补偿中子曲线，使得M4的其余曲线可以作为训练数据发挥作用，利于提升模型精度。对于测试井而言，T2井的深电阻率曲线包含5 757个数据点，但其中64%的数据值为99 990(主要位于2 700～3 200 m井段)，猜测是测量故障或超出测量上限后产生的截断值，因此作为待生成的未知曲线看待。

最终，清理前后的数据情况如表2所示，数据处理后展现出训练数据存在多源复杂特征：①M2和M3井数据量较少；②M5井的测井深度与其余训练井具有较大差距；③M4缺少补偿中子数据，通过长短期记忆神经网络生成作为填充。

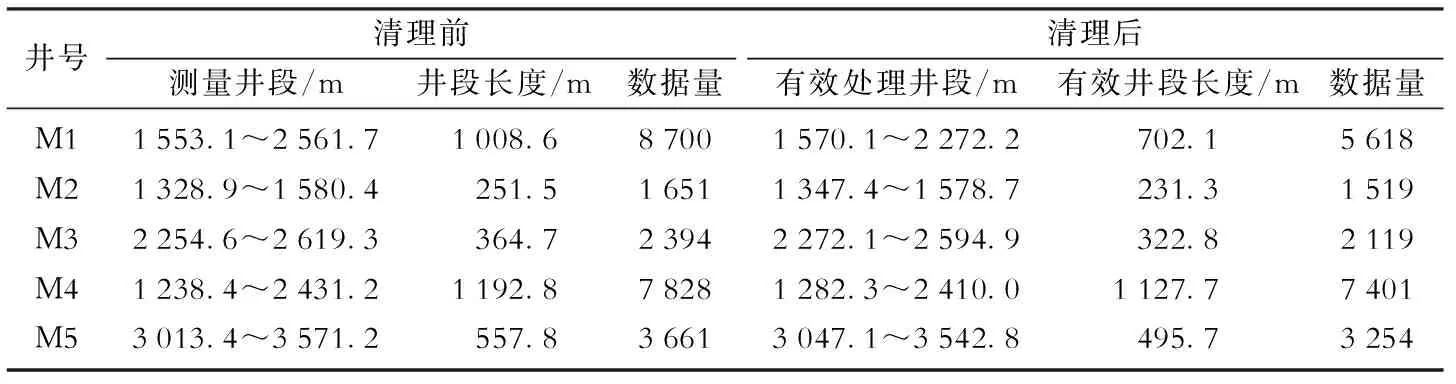
表2 数据清理前后数据情况对比Table 2 Comparison of data before and after data cleaning

3.3 模型选择

本研究采用的是长短期记忆神经网络(LSTM)，它的网络结构中具有一个循环，可以将某一计算步的结果作为新的输入的一部分，传入下一计算步中[15]。这种方式保证了信息可以在不同的计算步之间传递，使得模型有能力处理序列数据。长短期记忆神经网络的神经元中包含有4个交互层，分别是遗忘门层、输入门层、双曲正切层和输出门层,其中遗忘门层(式(2))决定此前计算步中哪些信息被舍弃(遗忘);输入门层(式(3))决定当前步输入中哪些信息被保留(记忆);双曲正切层(式(4))可以基于当前步的输入产生候选值。根据遗忘门层和输入门层的信息可将不同计算步的信息进行融合(式(5))，该步是LSTM可以处理序列数据的关键。最终输出门层(式(6))产生输出结果。上述4个门层中都包含有权重和偏置，在模型训练过程中通过训练数据学习获得。

ft=σ(Wf[ht-1,xt]+bf)

(2)

it=σ(Wi[ht-1,xt]+bi)

(3)

(4)

(5)

ht=σ(Wo[ht-1,xt]+bo)tanh(Ct)

(6)

交互门层使得神经网络具有动态的记忆与遗忘能力，能够更好地处理具有长期相关性的数据。由于测井曲线的采样间隔较小，而地层厚度往往可达20～50 m(即相互影响的序列长度包含上百个数据点)，所以测井曲线生成问题适合使用长短期记忆神经网络进行处理。

3.4 基于交叉检验的模型评估

为了判断模型是否适合当前问题，引入机器学习中的交叉检验方法[16-17]。从本质上讲，交叉检验是一种重采样方法，尤其适用于数据量不足的情况。首先将数据随机分成m份，然后取其中1份作为测试集，其余m-1份作为训练集以构建模型，最后在测试集上评估模型效果并记录。重复上述过程m次，直至每1份数据都作为测试集评估过1次。最后将m次评估结果取平均，作为模型的性能评价结果。

交叉检验能够在数据量有限情况下尽可能充分利用全部数据且易于操作，在机器学习中应用广泛。考虑到测井曲线获取成本较高，为进一步降低数据需求，本文采用一种特殊的留一法交叉检验[18-20]。该方法中，分组数目m与样本总量一致，能够最大限度利用有限的训练数据。

3.5 基于收敛性分析的模型训练

在构建测井曲线生成模型时，测试井的数据分布可能与训练数据的分布不同。机器学习算法在非同分布的数据上难以保证预测效果，因此需要针对具体预测井进行分析以预估模型的适用性。本研究通过收敛性分析在未知待生成数据的分布的前提下，对模型效果进行预估。首先，基于同一训练集独立训练多个机器学习模型，然后分别生成目标测井曲线。采用不同实验生成值的标准差作为收敛性判断依据，标准差越大则说明收敛性越差，当前数据分布差异越大，结果可信度越低。最后，采用集成学习中的投票算法融合不同模型的结果[21]。

在投票过程中不同模型采用不同的权重，权重是根据对应模型预测结果与整体预测结果的偏差来决定的，偏差越大则该模型预测结果可信度越低，对应权重越小。采用均方误差(mean square error，MSE)作为计算偏差的标准(式(7))。权重的计算如式(8)所示，该方法保证所有模型的权重之和为1，且误差越小的模型权重越大[22]。最终通过式(9)将所有模型的结果进行融合。该方法与直接对各个模型求平均不同，后者直接根据每个样本点处的结果进行投票，只利用了局部信息。而本方法的权重根据整体预测结果获得，参考的是全局信息。

(7)

(8)

(9)

当模型收敛性较差时，说明每个模型预测结果的可信度都不高，相当于产生了诸多同质的弱学习器，利用投票算法将弱学习器的结果进行组合，可以产生能力更强的强学习器，提升模型预测精度。收敛性分析方法可以对具体某一口待生成井的预测结果进行预判，当结果可信度差时，通过集成学习中的投票算法提升模型精度。

4 实验结果与案例分析

4.1 数据完整性与数据补全效果分析

本案例基于长宁威远7口页岩气井的实测数据验证建模范式的效果。首先，在训练集存在数据缺失时，通过模型对缺失数据进行补全，然后作为已知值用于后续训练。为了验证补全数据的效果，我们将原始数据中M4井的补偿中子测井曲线隐去(表1)。

图2为M4井补全的补偿中子曲线和真实补偿中子曲线在目的层段(2 310～2 410 m)的对比结果，其中橙色曲线为被隐去的真实值，蓝色曲线为模型生成结果。可见生成的测井曲线能够捕捉真实曲线变化趋势，在目的层段具有较高精度。因此，建模范式中的数据完整性分析和补全方法可用于构建训练数据集。

图2 M4井目的层段补偿中子测井曲线Fig .2 Compensated neutron log in the target formation of Well M4

4.2 模型选择及交叉检验结果分析

长短期记忆神经网络能够处理具有长期相关性的序列数据，理论上可以解决测井曲线生成问题。但是，对于一个具体问题，模型的输入和输出的测井曲线间的映射关系可能非常复杂，因此在实际应用需要通过留一法交叉检验进行验证。以T1井生成无铀伽马曲线为例，对训练集中的5口井进行交叉检验，即每次实验利用4口井训练模型，用剩下的1口井做测试，重复5次实验以遍历训练井。根据5次实验结果评价模型精度，当模型结果满足要求时认为模型可以解决当前问题，然后再用全部5口训练井的数据训练模型，生成测试井中的缺失测井曲线。

M1至M5井的无铀伽马测井曲线交叉检验结果如图3所示，从上至下分别对应M1到M5井作为测试井时的生成结果，橙色曲线为真实值，蓝色曲线为预测值。可见长短期记忆神经网络的生成结果与真实值相近，说明该模型可以用来解决无铀伽马曲线的生成问题。在其余测井曲线的交叉检验中也得到了令人满意的结果。

图3 无铀伽马曲线交叉检验结果Fig .3 Cross validation results of Uranium-free gamma log

4.3 收敛性分析

收敛性分析用于评估待生成曲线的数据分布与训练数据是否相同。在本研究通过重复10次实验分析收敛性。图4展示了T1井横波时差的预测结果，可见10次独立实验的预测值收敛，说明T1井的数据分布与训练集基本一致，模型预测结果准确可信。

图4 T1井横波时差曲线10次独立实验结果收敛性分析Fig .4 Convergence analysis of 10 independent experiments of shear wave time difference log of Well T1

T2井虽然在深层(目的层段)收敛性较好，但是在浅层的收敛性较差，如图5所示。该实验结果说明T2井浅层部分的数据预测难度较高，模型预测结果可信度相对较低。这一现象可能是由于T2井在特征空间上的数据分布与训练井不同，这也与3.2节中针对T2井数据处理发现的问题相符合。如果能够获得更丰富的训练数据，扩充训练数据分布范围，模型在T2井浅层处的收敛性将会得到提高。

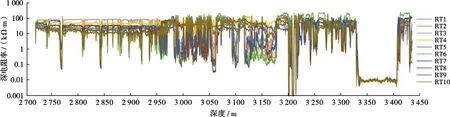
图5 T2井深电阻率测井曲线10次独立实验结果收敛性分析Fig .5 Convergence analysis of 10 independent experiments of deep resistivity log of Well T2

4.4 生成曲线精度分析

将T1井和T2井的全部生成结果与人为隐去的实测测井曲线进行对比，以验证建模范式的效果。图6a展示了T1井目的层段的测井曲线，其中机器学习模型生成的测井曲线添加了“_Pred”的后缀。由图6a可知，生成的横波时差曲线与真实测量结果相近且趋势相同，在2 170～2 180 m预测的DTSM_Pred与实测DTSM曲线吻合较好，但2 180～2 205 m预测值存在偏移。此外，机器学习模型还成功生成了T1井实际没有测量的能谱曲线，根据图6a可知，T1井的GR曲线与CGR曲线能够有效分离，与物理规律相符，铀曲线峰值层段与地质上富有机质层段深度基本一致，说明该模型的生成结果具有一定的可靠性。此外，生成的PE曲线值在2～4 b/e，且在2 196～2 197 m区间PE曲线变高，与该储层深度碳酸盐岩含量升高特征一致(方解石的Pe值)，结果符合已知邻井地层的对应的岩石物理响应特征情况。

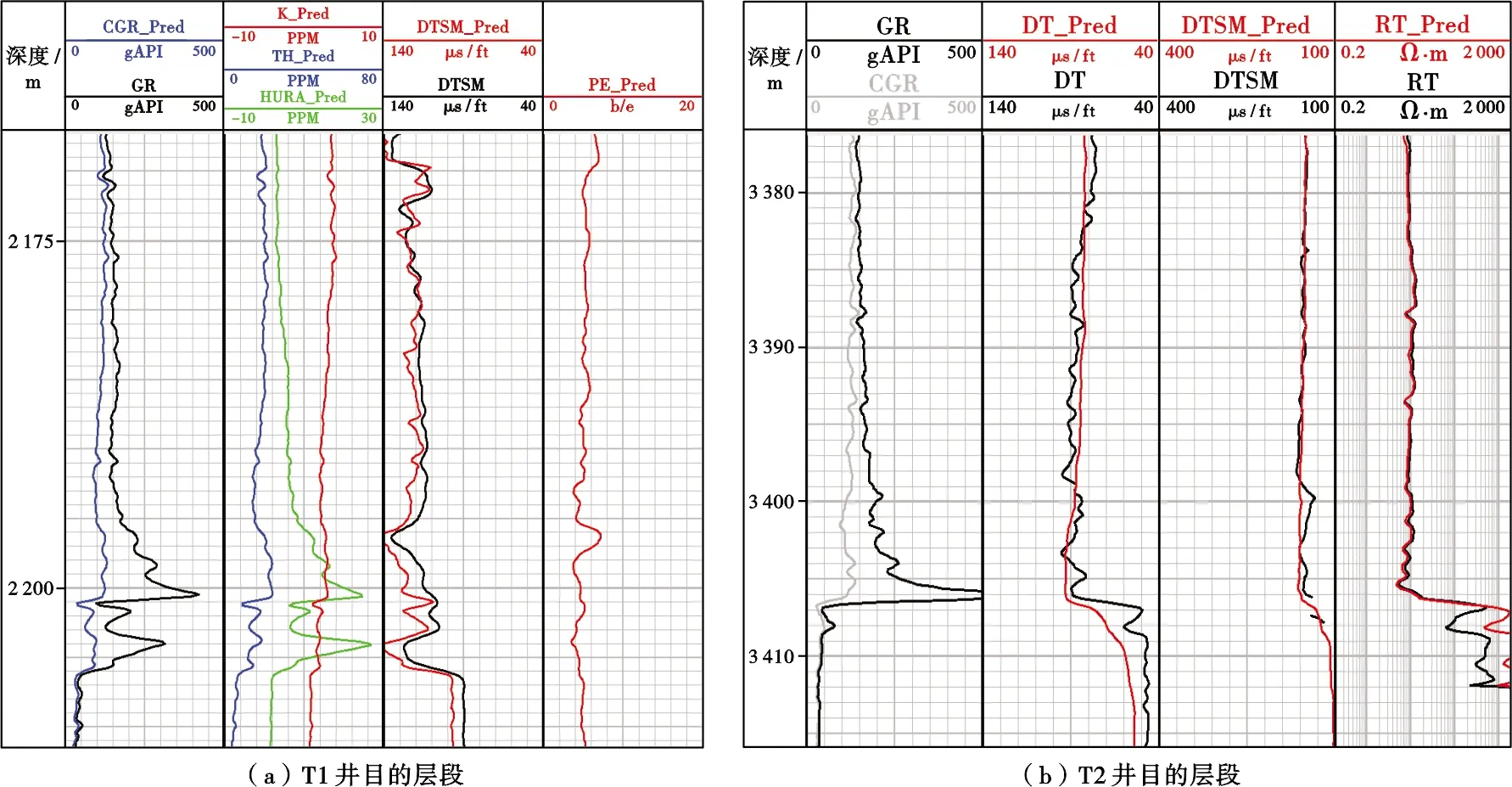
图6 实测测井曲线与生成测井曲线对比Fig .6 Comparison of the measured and generated logs

图6b展示了T2井目的层段的生成曲线结果，模型对于声波时差DT的预测，特别是细节刻画存在一定困难，具体表现在DT_Pred相对曲线平直，而实测DT曲线对GR曲线值变化存在一定波动，从岩石物理上解释，即声波在地层中传播时受岩性和物性的影响，而预测的DT_Pred曲线并没有表现出细节上的差异。虽然T2井在收敛性分析中表现不佳，但是其主要目的层段的收敛性相对较好(图5)，生成结果与真实值在趋势上基本一致，尤其是在页岩层段3 380～3 406 m，深电阻率曲线吻合程度相当高，能够应用于实际测井资料处理，评价页岩储层参数。

需要说明的是，T2井的电阻率曲线(RT)的实测数据中有64%的数据存在测量问题，是典型的由于测量问题而无法获得准确测井曲线的场景。虽然存在较多的制约因素，机器学习模型准确预测出T2井RT的变化趋势。由于测井解释中曲线的趋势变化是判断的重要参考，因此虽然预测值的绝对数值并不准确，但是模型生成的T2井RT曲线在实际开发中具有参考价值。

5 结论

1) 针对测井曲线生成模型的建模流程进行优化，本文提出了一套高效建模范式，解决了多源复杂测井曲线生成困难的问题。该建模范式首先通过数据处理提升数据质量和数量，然后利用交叉检验确保模型具有足够的能力，最后利用收敛性分析评估数据分布情况，确保生成的结果是可靠可信的。

2) 利用长宁威远页岩气区块的真实测井数据进行了实验，结果显示基于建模范式构建的机器学习模型生成的测井曲线与真实值接近，且符合已知的地质情况，验证了基于机器学习算法的多源复杂测井曲线生成方法的有效性，可以作为实际油气开发的参考。