基于改进霍夫变换的角度检测算法
阮殿旭
(沙洲职业工学院,江苏 张家港 215600)
引言
在机器人零配件生产装配等过程中,对零件的关键尺寸和参数进行测量是整台机器人集成后的重要质量保证手段,其测量结果直接影响机器人的质量和后续工序能否正常进行。近年来,随着视觉技术的发展,在基于计算机视觉和图像处理技术的零件检测方面的应用越来越广泛,在机器人零件测量方面,直线检测和圆形检测应用最为普遍。其中直线和圆形的检测最经典的算法是霍夫变换(Hough Transform),经过多年发展和改进,从最初始的霍夫变换到各种改进型霍夫变换算法,已经成为一类最常用的庞大的算法族[1],经扩展后的霍夫变换也可以检测其他简单的图像结构,如椭圆等。
在初始霍夫变换基础上,通过参数变换和耦合等方面的改进,出现了很多改进算法。本文对采用区域划分和参数空间变换点聚集状态选择优化的方法进行改进,通过粒子群算法实现霍夫变换参数的优化,同时通过置信投票优化,去除懒惰粒子,降低算法的计算量,提高处理速度,同时提高目标物体的投票结果精度。
1 霍夫变换与粒子群优化
1.1 霍夫变换
初始霍夫变换是由Paul Hough 于1962年提出的图像处理中的一种特征提取技术。霍夫变换通过一种投票算法检测具有特定形状的物体,将图像空间中的图形检测对应为参数空间的投票统计,将图像空间和参数空间形成映射关系,在一个参数空间中通过计算累计结果的局部最大值,得到一个符合该特定形状的集合作为霍夫变换结果。通常将参数空间称作Hough 空间,投票的维数取决于检测图形的参数的个数。
霍夫变换原理是利用图像空间点与变换空间线的对偶性,将图像空间中检测的所有点参数变换到参数空间中成为相对应的线,选出参数空间中变换的多条曲线相交点,其对应横轴和纵轴的值作为图像空间线的参数,就是对应图像空间中的直线参数。但由于原始图像空间每个像素转换到变换空间都是一条曲线,为曲线交点投票,投票越多,该点所对应的图像空间的这条线检测目标的可能性越大,因此该类算法涉及大量的投票,虽然原理简单,但变换和投票需要大量的计算空间,运行速度慢、效率低,而且对于小尺寸的直线检测结果不够精确,很难满足实时要求和精度要求,从而影响了霍夫变换实际应用范围[2]。
霍夫变换是实现两个坐标空间的映射,由于图像上的像素数量大,所需的计算量就很大,占据大量内存,检测耗时严重,很难达到实时测量。因此,很多学者通过研究改进,提出了检测速度快、精度高的优化霍夫变换。Galambos 等使用梯度信息来控制投票过程,将像素正确地分配给一条线,以加速算法[3]。Matas 等提出概率霍夫变换,随机获取图像坐标系中的前景像素点,变换到Hough 空间,对极坐标上的曲线交点进行投票,根据投票数量找出最可能的直线[4]。Cheng Z 提出一种严格的随机霍夫变换方法,用小的随机样本集取代全部样本集进行预处理,以减少错误选择点[5]。陈阳等提出了基于约束优化的车道线识别算法[6],首先采用概率统计原理对车道线点集分类,依据分类情况投票判断车道线,其次采用极径极角约束优化在目标区域筛选目标车道线。张英涛提出一种基于精简粒子群优化的霍夫变换算法[7],采用精简粒子群优化算法对霍夫变换进行优化。李亚娣等提出了基于Canny 算子和Hough 变换的夜间车道线检测[8],在边缘图像底部区域中利用Hough 变换进行直线拟合,在斜率约束的基础上提取内侧车道线。
1.2 粒子群优化算法
粒子群优化算法(Particle Swarm Optimization)是一种群体智能进化算法,1995年由Eberhart博士和Kennedy 博士提出。粒子群优化算法模拟鸟群捕食行为,鸟群在一片食物源随机分布的区域找到最大的食物源(优化问题的全局最优解),寻找食物时,通过鸟群个体之间的信息交流,让其他鸟最终都能聚集到最大食物源处,也即寻找到区域内的最优解。
在n 维解空间中,粒子群优化算法初始化为一群随机粒子,表示为Bi= (b1,b2, …,bn),每个粒子包含两个属性,即速度和位置,粒子速度Vi= (v1,v2, …,vn),粒子位置 (x1,x2, …,xn),粒子通过更新速度和位置寻找最优解,更新的条件是跟踪不同位置的极值(pbest,gbest),其中:pbest为粒子群的个体最优位置,gbest为群体最优位置的n 维向量;更新计算使用式(1):
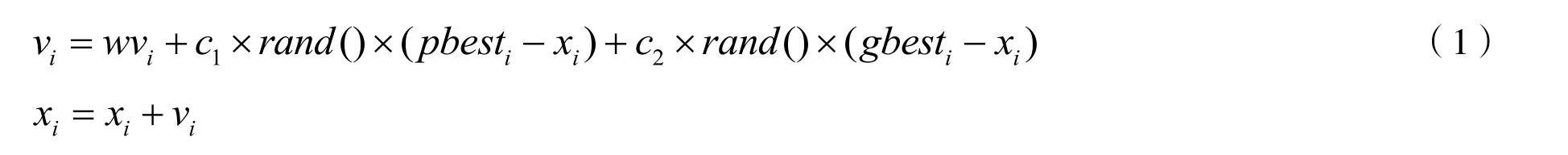
式中:ci,c2为加速常数,调节学习步长;rand()为随机函数,取值范围在0-1 之间,以增加全局性;w为惯性权重,调节空间的搜索范围;i为当前粒子。
2 改进霍夫变换算法
将粒子群算法与霍夫变换相结合,同时引入投票优化策略。对原始图片的前景像素进行霍夫变换,把得到的变换空间参数作为粒子群个体的位置,使用粒子群优化算法寻找最优解,将霍夫变换的累加数组设置为适应度函数值,通过迭代得到最优的参数,在迭代过程中,引入投票优化策略,将每次更新的粒子中的“懒惰粒子”剔除,有助于提高运算效率。
在图像坐标系中,用y kx b= + 表示直线的方程,当直线角度为90 度,即k=∞时,b的取值无法满足计算,因此,将直线方程替换为极坐标方程如式(2):

原始图像坐标系中的一点P(X1,Y1),使用霍夫变换后得到式(3):

此时从图像坐标系变换到Hough 空间坐标系中,P(X1,Y1)一个点变换为一条正弦曲线,图像坐标系中一条直线变换到Hough 空间,则是一组有一个共同相交点的正弦曲线,并且这一组曲线的交点所对应的(ρ,θ) 即为原始图像坐标系中直线的参数。
改进的霍夫变换算法过程:
(1)确定初始粒子群为Q( 0) = {P1,P2…PN},种群规模为N,为极坐标系参数ρ和θ设置ρ0和0θ初始值,并将累加数组初始化为0;
(2)对原始图像进行基于Canny 算子的边缘识别,获得检测对象边缘点集合;
(3)在集合中随机任取两点P1和P2,计算P1和P2连接成一条直线,其斜率和截距参数作为粒子的初始化位置X0,并重复将所有任意两点组成的直线参数粒子都完成初始赋值;
(4)对每个种群粒子的速度进行初始化赋值V0;
(5)通过适应度函数,计算种群粒子的适应度值f(X0(k,ρ k,θk));
(6)种群粒子对最佳适应度值和当前适应度值进行比较,并根据适应度值更新种群粒子的位置P;
(7)从当前种群中选出最佳适应度的位置作为全局最佳值;
(8)对参数空间中的交叉点进行投票统计优化,将一些进化效果不明显的“懒惰粒子”剔除;
(9)更新下一代进化时种群粒子的速度;
(10)更新种群中粒子的位置;
(11)返回第5 步,重复执行,直到迭代完成。
3 算法测试
实验测试硬件环境:计算机(CPU 主频3.40GH,内存4G),软件环境:VC++6.0。图像对象为Buddy6F 型号的六轴协作机器人减速器盘型零件,检测目标利用霍夫变换检测直线确定V 型角的角度。
3.1 兴趣区域选择
通过对图像进行具体分析可知,如果对整个图片进行处理,需要更大的计算量和内存。在本文中确定需要检测的目标位置为盘类零件的端部(带有V 型槽),用Opencv4.3 库进行编程,实现对V 型槽区域ROI 的操作。
使用到的函数:矩形的表示 Rect 类>Rect(x,y,width,heigh)。
Rect 类的成员变量有x、y、width、height,分别定位在图片的左上角点的坐标和选择区域的宽和高。结果如图1、图2 所示。

图1 机器人减速器盘形零件实图
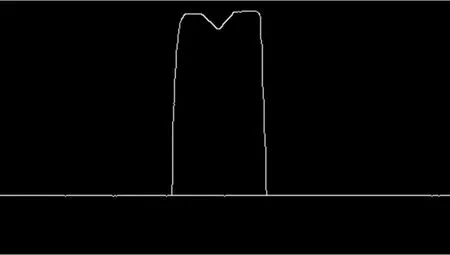
图2 机器人减速器盘形零件局部兴趣区域图
3.2 执行步骤
算法按照以下步骤完成:
(1)控制相机拍摄目标图片;
(2)利用OPENCV 相关函数实现兴趣区域的选择和截取;
(3)对图片中V 型夹角的两条边进行改进的霍夫变换,找出边线,测量角度。
3.3 测试结果
测试结果如图3、图4 所示,两张图大小均为600×480。图3 是利用经典Hough 变换得到的结果,图4 是利用本文算法并且统计投票阈值80%时的粒子群优化检测结果。
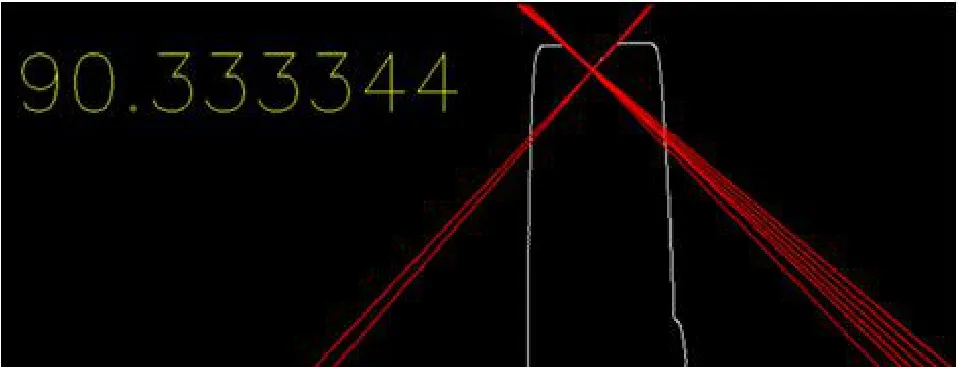
图3 利用传统霍夫变换得到直线检测图像

图4 利用80%投票阈值粒子群优化得到直线检测图像
用本文设计的算法(PSOCVHT)与概率霍夫变换算法(PPHT)、限制随机霍夫变换算法(RRHT)的性能进行比较,由对比结果(表1)可知,本文算法具有较高的效率和更高的检测精确度。
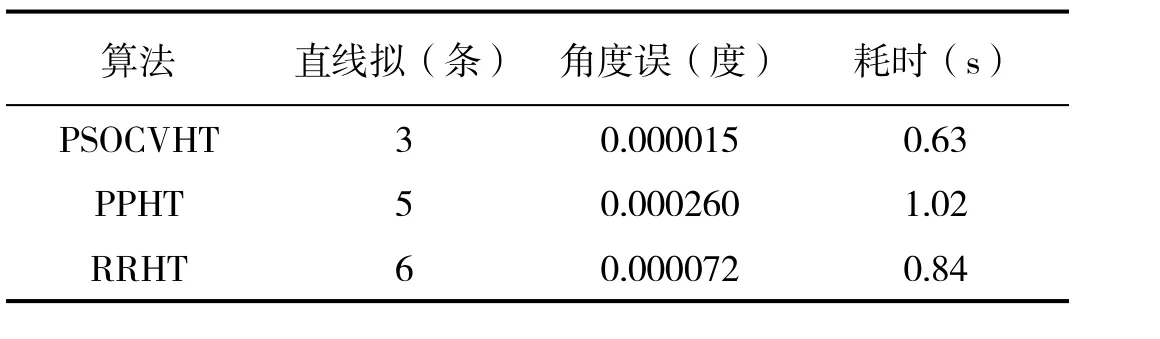
表1 PSOCVHT 与PPHT、RRHT 处理结果比较
4 结论
将直线图形的霍夫变换与粒子群算法相结合,并引入投票优化,提出了基于粒子群优化改进霍夫变换的协作机器人减速器盘类零件角度测量算法,该改进算法与利用传统Hough 变换检测算法进行了对比实验,结果表明:选用合理的投票阈值的粒子群优化算法对霍夫变换改进,不仅降低了霍夫变换的计算量,而且提高了角度检测的准确率。

